磁致伸缩-压电混合激励Janus换能器结构特征参量与纵振频率之间的关系∗

刘文钊 柴 勇 莫喜平

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

(3 北京海洋声学装备工程技术研究中心 北京 100190)

0 引言

水声换能器是进行水下探测和通信的关键设备之一，随着对海洋研究与开发的发展，低频、宽带、大功率水声换能器成为研究的热点之一。Janus 换能器是一种利用纵振动模态进行双面辐射的换能器，与传统Tonpilz 换能器相比具有更大的功率容量，并且可与其他振动形式进行组合实现宽带发射，例如Janus-Helmholtz 换能器[1−2]、Janus-Hammer Bell 换能器[3]、Janus-Ring 换能器[4]等。在20 世纪80年代，Butler 等[5]首先提出了磁致伸缩-压电混合激励的概念，由超磁致伸缩材料Terfenol-D 和PZT 压电陶瓷混合激励纵振动换能器，通过合理利用二者的振动相位差，实现一端振动减弱、另一端振动放大的效果。后续又研究并制作了混合激励Tonpilz 换能器[6−7]，利用二者在电路中分别呈感性和容性的特点，通过磁致伸缩材料控制低频工作模态、压电材料控制高频工作模态，有效拓宽了Tonpilz换能器的工作频带，并组成4×4阵列实现了宽带、大功率发射[8]。国内方面，刘强等[9]研究了磁致伸缩-压电混合激励Tonpilz 型换能器的线性数学模型，理论计算结果与实测结果较为一致。夏铁坚等[10]研制了2～7 kHz 磁致伸缩-压电混合激励Tonpilz 型换能器。柴勇等[11]将磁致伸缩-压电混合激励拓展至弯张换能器的研究中，在保持弯张换能器原有频率低、尺寸小等优点的同时，显著地拓宽了工作频带，并增大了辐射声功率。磁致伸缩-压电混合激励Janus 换能器至今未见有相关研究报道。本文对磁致伸缩- 压电混合激励Janus 换能器的结构特征参量与纵振动模态频率之间的关系进行了研究，总结归纳了各个结构特征参量变化对纵振动模态频率的影响规律，为此型换能器进一步的电声性能优化研究奠定了基础。

1 换能器的结构特征参量与特征模态

磁致伸缩-压电混合激励Janus 换能器在结构上具有旋转轴对称特征，同时左右两部分是对称的，因此可以选取其一半结构进行分析研究，结构示意图如图1 所示。换能器由5 个部分组成，分别是：磁致伸缩振子、压电振子、辐射头、中间质量块、尾部质量块。其中，磁致伸缩振子由Terfenol-D 棒及其两端的永磁体组成，压电振子由若干PZT压电陶瓷片并联堆叠组成。在其余部件的材料选择上，辐射头通常选择密度较小的铝，中间质量块和尾部质量块可选择密度较大的钢或者铜。

图1 磁致伸缩-压电混合激励Janus 换能器结构示意图Fig.1 Schematic diagram of magnetostrictive-piezoelectric hybrid Janus transducer

经过梳理后，换能器的主要结构特征参量共有12个，具体包括：(1)压电振子长度；(2)压电振子半径；(3)磁致伸缩振子长度；(4)磁致伸缩振子半径；(5)辐射头外半径；(6)辐射头内半径；(7)辐射头内高度；(8)辐射头外高度；(9)中间质量块高度；(10)中间质量块半径；(11)尾部质量块高度；(12)尾部质量块半径。

根据磁致伸缩-压电混合激励Janus 换能器的结构对称性，可以选取部分结构并施加对称边界条件后，建立有限元分析模型，如图2所示。

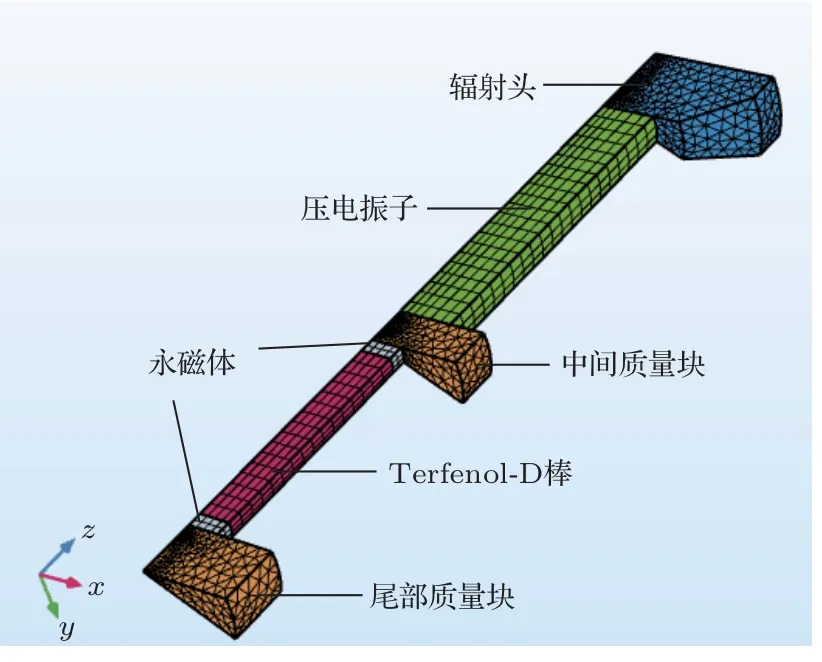
图2 磁致伸缩-压电混合激励Janus 换能器有限元模型Fig.2 Finite element model of magnetostrictivepiezoelectric hybrid Janus transducer

对于磁致伸缩-压电混合激励问题，使用压磁-压电比拟方法[12]可以将磁致伸缩机电耦合问题等效为压电耦合问题来解决。在有限元软件中输入各部分的材料参数，进行模态分析后，换能器前两阶特征模态的位移矢量图如图3 所示。第一种模态以磁致伸缩振子的纵振动为主导，经过压电振子的传递与放大，存在一个位移节点，位于尾部质量块，辐射头类似于平板活塞辐射，是一种理想的工作模态。第二种模态以压电振子的纵振动为主导，存在两个位移节点，分别位于压电振子的中部和尾部质量块，中间质量块的振动与辐射头反相，辐射头类似于平板活塞辐射，因此也是一种可以利用的工作模态。

图3 磁致伸缩-压电混合激励Janus 换能器特征模态图Fig.3 Two characteristic modes of magnetostrictivepiezoelectric hybrid Janus transducer

模态分析结果表明，磁致伸缩-压电混合激励Janus 换能器能够激发出两种有效的工作模态。相比之下，采用单一磁致伸缩或压电振子的Janus 换能器，只具有一个纵振动特征模态。因此对于磁致伸缩-压电混合激励Janus换能器，可以通过调整结构特征参量来实现两种工作模态的有效耦合，进而大幅拓展换能器的工作带宽。

2 结构特征参量与特征模态频率的变化规律

接下来对换能器的结构特征参量与特征工作模态频率之间的变化规律开展研究。在初始模型的基础上，通过改变某一个结构特征参量，同时保持其他结构特征参量不变，研究了各个结构特征参量变化对换能器特征工作模态频率的影响，以下模态1和模态2分别代表图3中第一种和第二种工作模态。

驱动振子的结构特征参量有4 个，分别为压电振子长度、压电振子半径、磁致伸缩振子长度和磁致伸缩振子半径。换能器两种工作模态频率与驱动振子各个结构特征参量之间的变化关系如图4所示：

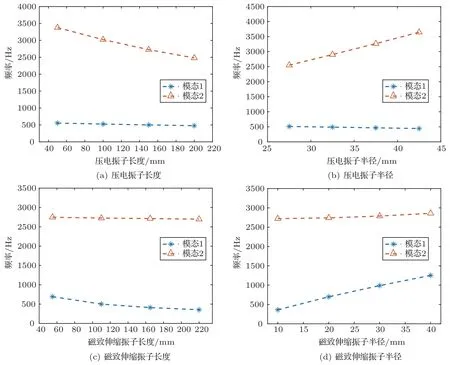
图4 驱动振子结构特征参量对工作模态频率的影响Fig.4 The influence of the structural parameters of the active sections on the frequencies of working modes

(1)随着压电振子长度增加，模态1频率小幅下降，而模态2 频率迅速下降，二者的频率差迅速减小；随着磁致伸缩振子长度增加，两个模态频率都下降，但磁致伸缩振子长度对模态1 的影响更大，二者的频率差逐渐增大。

(2)随着压电振子半径增加，模态1频率小幅下降，而模态2 频率迅速上升，二者的频率差迅速增大；随着磁致伸缩振子半径增加，两个模态频率都上升，但磁致伸缩振子半径对模态1 频率的影响更大，二者的频率差迅速减小。

辐射头的结构特征参量有4 个，分别为辐射头外半径、辐射头内半径、辐射头内高度和辐射头外高度。换能器两种工作模态频率与辐射头各个结构特征参量之间的变化关系如图5所示：

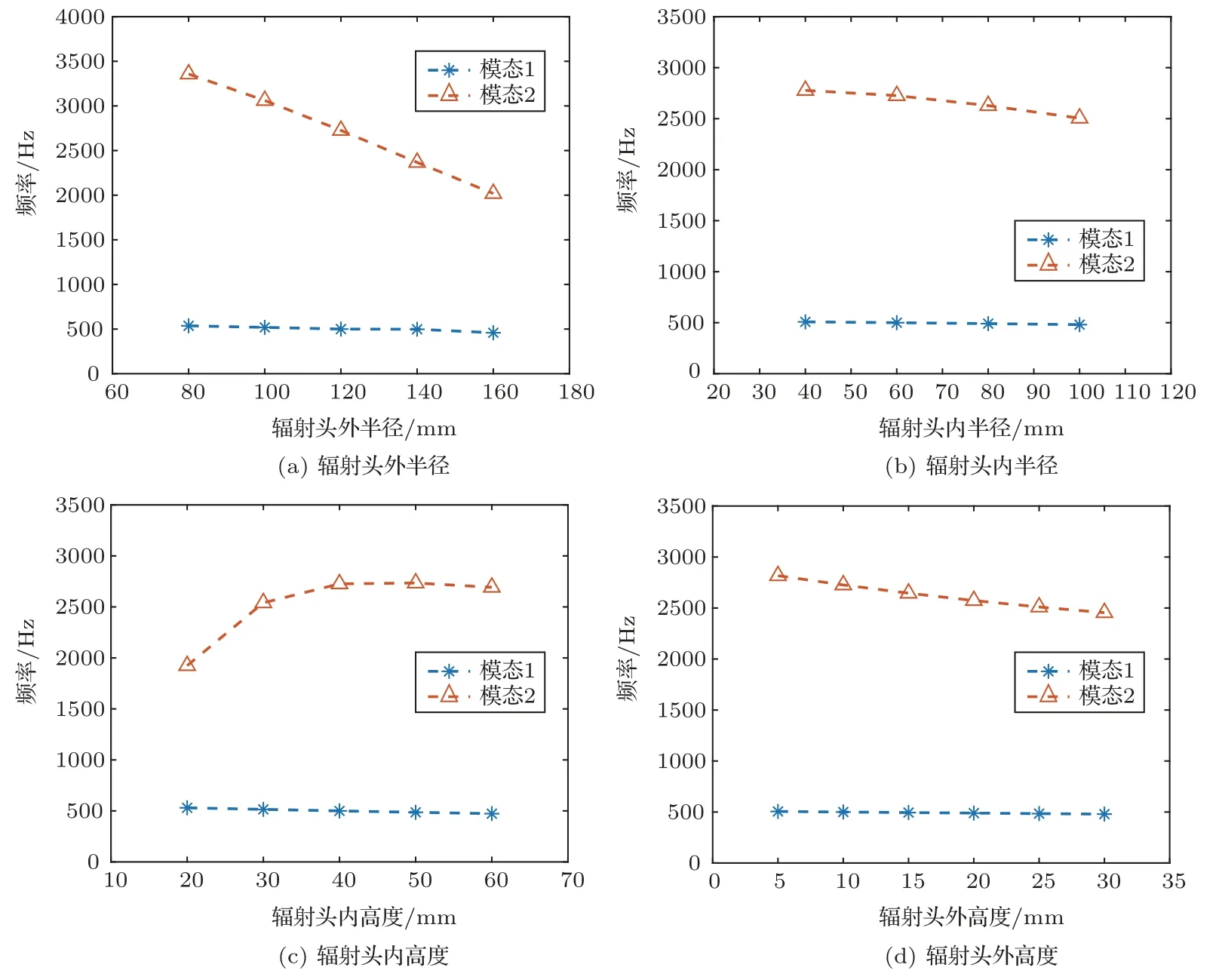
图5 辐射头结构特征参量对工作模态频率的影响Fig.5 The influence of the structural parameters of the piston mass on the frequencies of working modes

(1)随着辐射头外半径增加，模态1频率小幅下降，而模态2 频率迅速下降，二者的频率差迅速减小。随着辐射头内半径增加，两个模态频率均下降，但辐射头内半径对模态2 频率的影响更大，二者的频率差逐渐减小。

(2)随着辐射头内高度增加，模态1频率小幅下降，而模态2 频率先迅速上升后趋于稳定，二者的频率差迅速增大后趋于稳定。随着辐射头外高度增加，两个模态频率均下降，但辐射头外高度对模态2频率的影响更大，二者的频率差逐渐减小。

质量块的结构特征参量有4 个，分别为中间质量块和尾部质量块的高度与半径。换能器两种工作模态频率与质量块各个结构特征参量之间的变化关系如图6所示：

图6 质量块结构特征参量对工作模态频率的影响Fig.6 The influence of the structural parameters of the mass on the frequencies of working modes

(1)随着中间质量块高度增加，两个模态频率均缓慢下降，二者的频率差下降幅度很小；随着中间质量块半径增加，模态1 频率小幅下降，而模态2 频率迅速下降，两者的频率差迅速减小。

(2)随着尾部质量块高度或半径的增加，两个模态频率基本保持不变。

3 讨论

综合上述分析结果，进行如下讨论：

(1)由有源材料各结构特征参量对两个工作模态频率的影响可知，模态1 主要受磁致伸缩振子控制，而模态2主要受压电振子控制，这印证了磁致伸缩-压电混合激励的基本工作原理，换能器的两种工作模态分别由两部分振子控制，低频工作时主要由磁致伸缩振子控制，高频工作时主要由压电振子控制，但二者在工作时并非是孤立的，而是相互作用和影响的，其耦合作用机理需要进一步深入研究。

(2)辐射头各结构特征参量对模态2 频率的影响比模态1 更为显著。为了让换能器可以更好地辐射声能，原则上应该尽量增大辐射头外半径以增加有效辐射面积，同时减小辐射头内高度以降低辐射头的整体重量。需要注意的是，当辐射头外半径增大或辐射头内高度减小时，会倾向于激发出辐射头的弯曲振动模态，同时位于压电陶瓷中部的位移节点将逐渐上移至辐射头内部，形成部分振动反向区，有可能反而降低了辐射能力，因此需要仔细设计后来选择恰当的辐射头结构特征参量尺寸。

(3)调节中间质量块高度或半径都可以减小两个模态之间的频率差，调节半径的效果更大一些；而尾部质量块的尺寸变化对两个模态频率的影响微乎其微，由图3 的振动模态图可知，主要是由于尾部质量块基本都处于振动节点部位。因此，在确定合理的尾部质量块尺寸和中间质量块高度后，通过调节中间质量块半径就能实现改变两个模态频率差的效果。

从实现低频和宽带工作两个方面出发：若要降低换能器的工作频率，则应增大压电振子和磁致伸缩振子长度、减小压电振子和磁致伸缩振子半径、增大辐射头外半径；若要减小两个工作模态之间的频率间隔，实现模态的有效耦合，则应减小压电振子半径和辐射头内高度、增大磁致伸缩振子半径、辐射头外半径和中间质量块半径。

4 结论

本文对磁致伸缩-压电混合激励Janus 换能器的结构特征参量与纵振频率之间的关系进行了研究，通过将磁致伸缩-压电混合激励模式应用于Janus 换能器，证明了磁致伸缩-压电混合激励Janus 换能器具有两种纵振动模态，并进一步研究了其结构特征参量对工作模态频率的影响。经过有限元仿真计算，归纳总结了12个结构特征参量对主要工作模态频率的影响规律，所得结果为如何通过调节两种工作模态的频率间隔实现有效模态耦合并拓宽工作频带提供了一定依据。

由于超磁致伸缩材料Terfenol-D 具有应变量大、弹性模量低、能量密度大等特点，与压电陶瓷组成混合激励时，需要考虑二者之间的能量分配问题，否则压电振子的作用会被超磁致伸缩振子大大弱化甚至取代。因此，研究如何调整二者之间的能量分配、刚度匹配、驱动设计等，充分发挥磁致伸缩-压电混合激励的优势，在宽带工作这一优势基础上，进一步提升磁致伸缩-压电混合激励换能器的发射性能，也是今后研究工作中的一个重要方向。