T型三通水管路噪声特性数值研究∗

2022-05-16林鸿洲王献忠

应用声学 2022年2期

关键词：充液三通声压级

李宁陈林林鸿洲王献忠叶曦

(1 高性能船舶技术教育部重点实验室(武汉理工大学)武汉 430063)

(2 武汉理工大学船海与能源动力工程学院武汉 430063)

(3 中国船舶及海洋工程设计研究院上海 200011)

0 引言

船舶运行产生的振动噪声中，机械噪声占据着重要的位置。当主(辅)机等大型设备的机械噪声得到有效控制后，此时管路系统噪声对船舶总噪声的贡献便显得尤为突出[1]。船舶上大多数机械设备都通过各种油、水管路与船体结构相连，这给管路噪声的控制增添了难度；同时管路振动还会导致设备疲劳甚至断裂损坏[2−3]。一直以来，国内外学者们充分关注充液管路振动及流噪声的研究，但对水管路附件的流激振动噪声特性研究较少。目前，对充液管路振动及噪声特性的主要研究方法有实验方法以及数值仿真。Pittard 等[4]对完全发展的湍流管路进行振动实验，结果表明管道振动的加速度与流量之间存在一定的关系。Etim[5]研究管路内部流体流动对管道固有频率的影响，并将理论结果与实验结果进行比较。国内柯兵[6]对管路弯头的流致振动影响因素进行实验分析。宋佳朋[7]对通海管路管口辐射噪声实验研究。吴石等[8]采用小室测量方法测量充液管路流噪声，给出了流噪声的测量结果的影响因素。Zhang等[9]对弯管出口的噪声进行实验研究，发现弯头的振动特性及FW-H 声类比理论计算流噪声中的缺陷导致的数值仿真结果会略高于实验值。目前由于流噪声的测量还存在较多问题，对充液管路的实验研究主要集中在管路振动上，故基于大涡模拟(Large eddy simulation,LES)与Lighthill 声类比理论相结合的混合计算法得到广泛采用。Tan 等[10]采用LES 联合特征分裂(Characteristic-based split scheme,CBS)法研究圆形截面90◦弯管湍流流场。Zhang 等[11]以混合计算法[12]研究导流叶片对弯头的降噪效果。赵威等[13]对变截面管道流噪声进行计算。张咏鸥等[14]基于计算流体力学(Computational Fluid Dynamics, CFD)联合边界元(Boundary element method,BEM)的方法计算类阀空腔模型的流噪声，并证明利用该方法计算流噪声的可靠性。Mori 等[15]采用该方法对T 型截面管道在风机激励下的噪声特性进行分析。魏志[16]、方超等[17−18]发现管路附件的流激振动噪声远小于流噪声。

本文以文献[10]中的T 型三通管路为研究对象，进一步研究其振动噪声特性，计算T型三通管路的模态，开展厚度、流速对T 型三通管管口的噪声影响分析，获得流噪声和流激振动噪声的内在关系，为水管路附件的降噪设计提供了技术参考。

1 基本理论

1.1 LES模型

LES 模型在满足流体连续性方程、动量方程基本方程的基础上，对湍流变量进行滤波，得到滤波函数。经滤波后，得到的连续方程和动量方程分别为

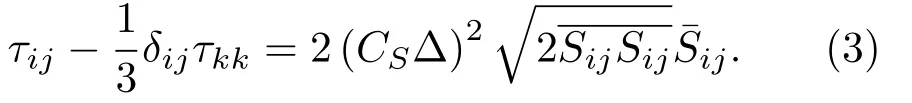
将式(3)代入式(2)后，可通过LES 模型获取完整流场信息。LES 模型是一种解决大尺度波动运动的方法，并且采用亚格子应力模式对小尺度湍流运动进行模拟。考虑到直接数值模拟(Direct numerical simulation, DNS)会消耗大量的计算时间，本文利用LES 模型模拟湍流流动对充液管路的流动问题进行计算分析。

1.2 Lighthill声类比

通过对源于N-S 方程的连续性方程及动量方程进行简化，获取Lighthill基本方程：

式(4)中，Tij为Lighthill 应力张量，其中Tij=ρuiuj −τij+δij(p −c20ρ)。Lighthill 声学类比理论将流场与声场联系起来，基于前期获取的流场信息求解声场。

1.3 声-固耦合方程

为了求解声-固耦合模型，必须同时求解与声场和结构相关的方程。通过考虑结构与声场的相互影响，声固耦合方程为

其中，Mf、Cf和Kf分别为流体等效质量、阻尼和刚度矩阵，Ms、Cs和Ks分别为结构质量、阻尼和刚度矩阵，U和P分别为结构位移矢量和声压矢量，Fs为结构载荷力向量。

2 数值仿真方法

2.1 模型构建

本文以文献[10]中的T 型三通管为研究对象，其截面为边长D= 100 mm 的正方形，如图1 所示。计算模型进流段与去流段的长度均为10D，原点设置在T 型管进出流的交界处。假定T 型三通管为钢质方形管，其密度ρ= 7850 kg/m3，泊松比为µ= 0.3，弹性模量为E= 2.06×1011Pa，结构阻尼因子η= 0.01。其入口处的流动被假定为已经完全发展的湍流，其流体介质为水，水中声速为c=1500 m/s。

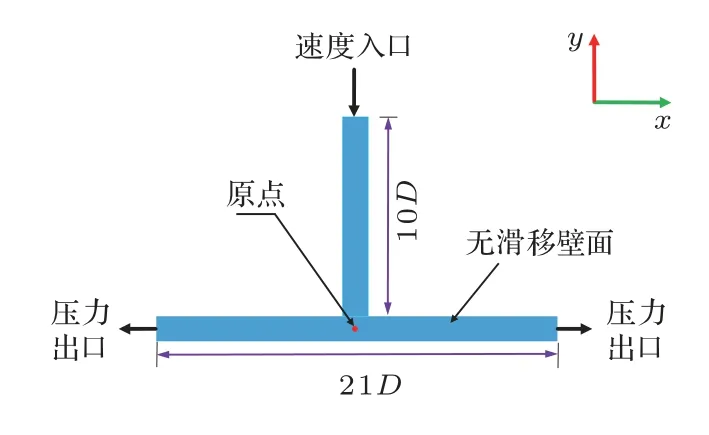
图1 T 型三通管几何模型图Fig.1 Geometric model of T-shaped tee pipe

2.2 湍流流场仿真

如图1 所示，T 型三通管计算模型的计算域由出入口、固体壁面组成，定常流速的速度入口边界条件应用于管路入口，零压力出口的压力出口边界条件应用于管路出口，无滑移的壁面边界条件应用于管壁，其中速度边界以及压力边界均基于湍流强度及水力直径(Intensity and hydraulic diameter,IHD)方法进行湍流设定。采用六面体结构化网格对其流体域进行网格划分，并考虑到流向突变处湍流强度变化，对该区域的局部网格加密处理，如图2所示。由于涉及到边界层计算的精度问题，经过网格无关性验证，发现流体域网格模型第一层网格质心至壁面的距离设置为0.16 mm，网格增加率设置为1.1，六面体网格总数量达到28×104时，可满足计算精度要求，且所有流体网格质量均在0.8及以上。

图2 T 型三通管网格划分图Fig.2 Meshing diagram of T-shaped pipe

基于雷诺时均法的realizablek-ε湍流模型，开展流速为2 m/s、4 m/s、6 m/s、8 m/s、10 m/s、12 m/s 时T 型三通管定常流动流场数值模拟，以定常的计算结果作为非定常计算的初始流场，基于LES 模型对T 型三通管瞬态流场进行数值计算。由于瞬态流场的计算步长需与声场的计算频率相结合，对一个时间序列做快速傅里叶变换后，可分析结果的最高频率为0.5∆t−1。由于本文声场分析频率范围取为10～1000 Hz，故设置时间步长为2×10−5s，可满足计算要求。

通过残差分析以及对T 型三通管出口质量流等指标的监测，发现当迭代500步后，瞬态流场基本趋于稳定状态，此时打开FW-H 声类比模型，对壁面的脉动压力声源进行提取，作为后期声场计算的初始数据。

3 数值计算结果

3.1 模态分析

基于有限元(Finite element method,FEM)法，计算充液T 型三通管前四阶声学模态。从图3 中可知，高声压区被低声压区所分割，形成特殊的“节线”。随着声学模态阶数的增加，固有频率值基本成倍数增长，节线数目也开始增多，节线的产生主要是因为驻波的形成，使该处的声压值达到最小值。相对比充气管路，充液管路阻抗与水介质阻抗相当，必须考虑水介质对管路声振特性的耦合影响。

图3 前四阶声学模态Fig.3 First four acoustic modes

基于边界元(Boundary element method,BEM)法，对不同厚度下的T 型三通管进行结构模态与耦合模态计算，低阶固有频率对比结果如图4 所示。图4 中第一列的5 条曲线所代表的是结构干模态的固有频率，第二列的5 条曲线所代表的是耦合湿模态的固有频率。从图中可知，随着管壁厚度的增大，结构干模态和湿模态的固有频率均逐渐增大。考虑计及声固耦合作用，湿模态固有频率值出现明显的减小，这是由于考虑了重密度的声介质，相当于增加了管路附连水质量，导致固有频率往低频移动，说明在充液T型三通管路中，声介质对结构模态有着较大的影响。

图4 固有频率对比图Fig.4 Natural frequency contrast diagram

3.2 流噪声分析

基于混合计算法，运用声学计算软件对不同流速下的充液T 型三通管路进行流噪声计算，其声压级频谱图如图5 所示。为了更方便分析，其1/3倍频程声压级频谱图如图6 所示。由图5 和图6 可知，T型充液管路管口流噪声呈现随频率增大其声压值逐渐较小的趋势，流噪声能量主要集中在低频段。由于管内介质在截面形状突变处及流速方向变化处产生湍流，并伴随着大量的旋涡，进而导致流噪声的产生。根据涡声理论，管内流速等量增加，但旋涡产生并没有表现出线性的增长速率。此外，不同流速下的声压级频谱曲线在360 Hz 及720 Hz 处都出现了峰值，这与声学模态的前两阶固有频率相近。随着流速增大，其声压级频谱图中的峰值频率保持不变，说明流速并不是影响流噪声频谱曲线峰值频率特性的主要因素。图5 中的红色圆圈位置代表的是管路声学特性影响流噪声的位置，说明管路的声学特性决定着流噪声的峰值频率。

图5 流噪声声压级频谱图Fig.5 Spectrum diagram of sound pressure level of flow noise

图6 流噪声1/3 倍频程声压级频谱图Fig.6 Spectrum diagram of 1/3 octave sound pressure level of flow noise

3.3 流激噪声分析

管路噪声不仅有脉动压力直接辐射所产生的流噪声，还包括脉动压力作为激励所产生的流激噪声。运用声学计算软件，基于声-固耦合法对不同流速下的充液T 型三通管路进行流激噪声计算，其计算结果如图7、图8 所示。由于流激振动涉及到结构属性，此次计算以管壁4 mm 为例。由图7 可知，与流噪声相比，流激噪声主要集中在中频段，声压级大小呈现出“先增大，后减小”的趋势，这与流噪声的频谱特性存在差异。流激噪声峰值除了出现在声学模态处，还出现在众多的耦合模态处。图7 中红色圆圈位置代表管路声学特性影响流激噪声的位置，天蓝色代表的是结构振动特性对流激噪声影响的位置，说明管路的流激噪声不仅与管路声学特性有关，也与结构的振动特性相关。

图7 流激噪声声压级频谱图Fig.7 Spectrum diagram of flow-excited noise pressure level

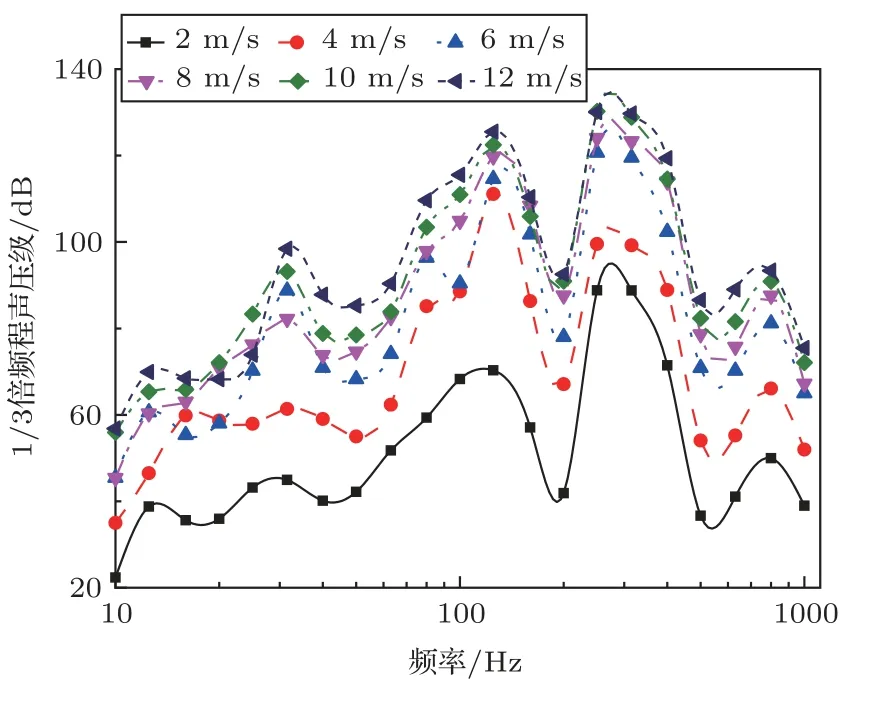
图8 流激噪声1/3 倍频程声压级频谱图Fig.8 Spectrum diagram of 1/3 octave sound pressure level of flow-excited noise

从图9可知，随着管壁厚度的改变，其模态发生变化，导致各厚度下的流激噪声的峰值频率出现得较为混乱。360 Hz 和720 Hz 处流激噪声不受厚度因素控制，均受到管路声学特性的影响而出现峰值。高壁厚管在某些频段可以有效地抑制流激噪声，但是在某些峰值频率处的噪声值也会出现高于低壁厚管的情况。

图9 4 m/s 流速下各厚度流激噪声对比图Fig.9 Comparison of flow-excited noise at the velocity of 4 m/s with different thickness

3.4 流噪声与流激噪声对比

将不同流速下三通管的流噪声和流激噪声进行对比。如图10 所示，流噪声能量集中在低频段，而流激噪声的能量主要集中在中频段，所以在低频(10～100 Hz)内，流噪声的幅值远大于流激噪声。在100～400 Hz 频段，流激噪声出现了较多的峰值点，此频段内更多的耦合模态被激发，导致流激噪声的幅值超过流噪声。在400～1000 Hz频段，流噪声的幅值大于流激噪声，且在声模态处，两者均存在着峰值。随着流速的增大，流噪声与流激噪声的幅值都增大，但流噪声的增量大于流激噪声的增量，这是由于流噪声更依赖于湍流的漩涡发声。

图10 流噪声与流激噪声对比图Fig.10 Comparison of flow noise and flow-excited noise

将不同厚度下三通管的流噪声和流激噪声进行对比。如图11所示，壁厚度为1 mm时，流激噪声在中低频(720 Hz之前)，其声压级幅值大于流噪声；在高频(720～1000 Hz)，流噪声声压级幅值超越流激噪声。在2 mm 壁厚时，在低频(10～100 Hz)时，流噪声与流激噪声幅值基本一致；但在中频，流激噪声的幅值在耦合模态固有频率处出现了峰值，导致流激噪声的声压级幅值大于流噪声；同样，在高频出现了与1 mm 壁厚的情况，即流噪声的幅值大于流激噪声。壁厚达到3 mm 以后，中低频情况类似，但在高频处流噪声的幅值大于流激噪声的趋势越来越明显。