一种基于特征点提取的扬声器异常声检测方法∗

宋华建 穆瑞林 周子奇

(1 天津科技大学机械工程学院 天津 300222)

(2 天津市轻工与食品工程机械装备集成设计与在线监控重点实验室 天津 300222)

0 引言

扬声器异常声检测是扬声器出厂前必须进行的重要流程。传统的异常声检测采用专业声音检听员以人耳检测为主，由于检听员存在易疲劳、主观性强、长时间工作损害听觉系统等问题，传统检测方法已很难满足高精度、大批量快速检测的需求[1]。近年来大量学者对扬声器异常声检测方法进行研究，Brunet等[2]应用短时傅里叶变换分析扬声器响应信号的时频图，并对合格扬声器与故障扬声器时频图做频谱差异性分析；Wang 等[3]将扬声器响应信号短时傅里叶变换时频图进行区域划分，并用高阶频率均值大小反映扬声器的异常声差异程度；Temme 等[4]基于人耳感知模型对扬声器异常声检测进行探究；李宏斌等[5]提出基于短时傅里叶变换的扬声器异常声检测方法，并构建分割矩阵，通过与黄金样本对应矩阵的距离判断扬声器是否存在异常声故障；张平等[6]提出声频质量感知评价(Perceptual evaluation of audio quality, PEAQ)算法在扬声器异常声检测中的应用，将人耳听觉模型巧妙地应用于检测系统的构建，并在实验室条件下对该方法的可行性进行了验证；祝仰宽等[7]在扬声器异常声故障检测方法研究中提出时频图各阶能量均值在检测中的应用，并将待测扬声器各阶谐波带能量均值与标准能量差值做比较得出结论；周静雷等[8]提出VMD-Hilbert 变换在扬声器异常声检测中的应用，对比得出其变换所得时频矩阵与标准矩阵的差异更大；周晓东等[9]探究了窗函数在异常声检测中的应用，并针对不同窗函数特性做了对照分析；郭庆等[10]提出基于心里模型和支持向量机的扬声器异常声检测方法，通过对检测系统及相关参数的优化，得到了较好的检测效果并可实现部分异常声故障的分类。

上述检测方法中，未充分考虑整体检测系统数据处理量及检测效率，对系统运算量要求较大。且基于短时傅里叶变换的检测方法在检测模型构建过程中存在有效特征不确定性，高次谐波均值法及谐波带内能量均值法均在对大量数据进行平均化处理的基础上进行，使有效特征被平均化处理。本文基于改进尺度不变特征转换(Scale-invariant feature transform, SIFT)算法提取特征点，以小样本统计学原理构建有限数量特征点模板，可有效降低数据处理量；对特征区域的归类，还可实现扬声器故障分类。

1 检测信号的提取及分割

扬声器异常声可能由多种问题产生；在本研究中针对普通扬声器的异常声样本与合格样本进行区分。根据扬声器特性以及检测需求，设计对数回扫信号激励扬声器发声；经传声器声电转换后由采集卡采集，截取信号有效数据做短时傅里叶变换得到如图1所示时频图，具体方法见文献[5]。

图1 扬声器时频图Fig.1 Time-frequency spectrum of loudspeaker

为进一步分析，本研究对上述时频图进行分割处理。基本过程如下：提取50 个合格扬声器经短时傅里叶变换所得矩阵Ma(a= 1,2,··· ,50)的各列最大值所在位置，即：max(Ma(i,j)),(i=1,2,3,···)，记录对应点纵坐标j值，确定各列极大值点Aa(i,j)位置，并在该点上下各取一点Aa(i,j+1)及Aa(i,j −1)，将所有Aa点填入矩阵Ma的同型零矩阵内得到矩阵Na，以式(1)求取基波带矩阵，并将矩阵内大于0 的元素均替换为1，构建基波带模板矩阵。

式(1)中，NJ为基波带模板矩阵，Na为单个扬声器基波带矩阵，a为合格扬声器编号。

以基波带矩阵NJ内赋值点A做如下位置变换A(i,b×j−1)，A(i,b×j)，A(i,b×j+1)，b=2,3,4,···得到单谐波带提取模板矩阵Nb，将N1至N7相叠加并做平滑处理得到谐波带模板矩阵NX，其时频图如图2(a)所示；将七阶以上部分作为高次谐波域模板矩阵NG，其时频图如图2(b)所示。

图2 特征分割模板Fig.2 Segmentation template of feature points

2 特征点提取及模型建立

2.1 算法实现

由Lowe[11]提出的SIFT 算法具有较好的鲁棒性，且相较于深度卷积神经网络可提取出较精确的特征点位置并进行特征匹配。

在本研究中，以合格扬声器及异常声扬声器二维时频图为待处理样本，应用尺度可变高斯函数(如式(2))[12]，与扬声器二维时频图进行卷积(如式(3))[11]，完成空间尺度变换。

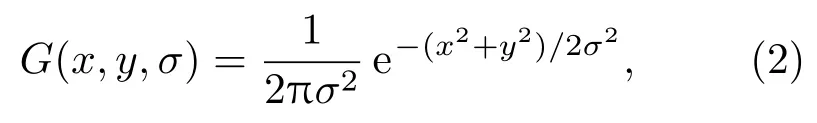
式(2)中，G(x,y,σ)为高斯卷积核，σ为高斯变换因子(本研究中取0.6)，x为像素点横坐标，y为像素点纵坐标。

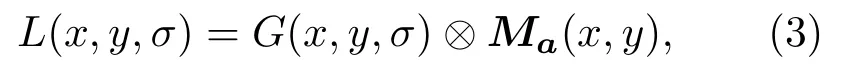
式(3)中，L(x,y,σ)为高斯尺度空间，Ma(x,y)为扬声器二维时频图矩阵。

为了进一步精确提取稳定的特征点，利用不同尺度的高斯核与扬声器二维时频图卷积生成高斯差分尺度空间：

式(4)中，D(x,y,σ)为高斯差分尺度空间，k为传递因子。

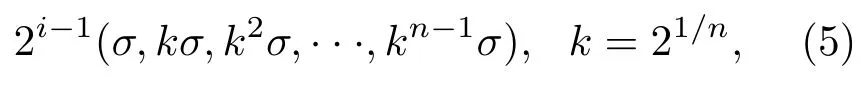
式(5)中，i为空间金字塔个数，n为金字塔层数。

利用式(5)的原则构建空间金字塔，由于本研究所涉及时频图大小、方向均有较强的一致性，故选空间金字塔数量i=5，层数n取3，构建空间金字塔。进一步提取极值点，以中间层采样点为中心构建3×3×3 的采样空间如图3 所示，将空间内的其余26点与采样点比较，如果采样点为极大值或极小值，则保留此采样点。

图3 采样空间[11]Fig.3 Sample space[11]

对尺度空间进行泰勒展开得式(6)，对其求导得式(7)，将其值置为0 则可求得对应x值，同理可得出y值，确定其位置信息。

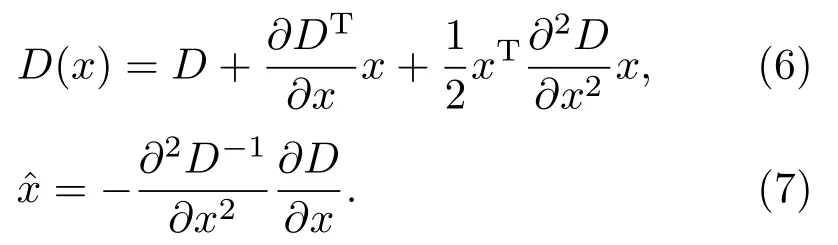
由于本研究中时频图不存在旋转问题，不考虑旋转方向对特征点提取的影响，直接进行特征点的匹配，并输出所提取出的总特征点位置，以及两时频图相匹配的特征点位置。

选取3 位专业声音检听员均认证合格的扬声器10 支，3 位专业声音检听员均认证存在异常声的扬声器20 支。应用上述方法分别提取每支合格扬声器特征点并填入矩阵Ma的同型零矩阵内，得到合格扬声器特征矩阵Pa(a取1,2,···,10)；并将每个合格扬声器分别与20 支异常声扬声器做特征点匹配，将所提取的匹配特征点填入矩阵Ma的同型零矩阵内，得到匹配特征矩阵Qa,k(k表示异常声扬声器编号，取1,2,···,20)，此矩阵反映出合格扬声器与异常声扬声器相关性较大特征点。将合格扬声器与异常声扬声器相关性较大的特征点从合格扬声器总特征点中剔除，得到合格扬声器特征点矩阵Za(即Za=Pa −Qa,k)。

2.2 特征点分析处理

将上文所述剔除相关性特征点的10 支合格扬声器特征点矩阵进行叠加处理，如式(8)所示，构建扬声器特征矩阵，其分布情况如图4所示。

图4 整体特征点分布情况Fig.4 The distribution of feature points on the time-frequency spectrum

式(8)中，Z为扬声器特征矩阵，Za为剔除相关性特征点的合格扬声器特征矩阵。

造成扬声器异常声的原因较多，其响应时频图特征存在差异性。为进一步减少中间状态样本数量，对特征矩阵进行谐波带域及高次谐波域划分，应用式(9)提取谐波带域特征点矩阵，并将该矩阵置于谐波带矩阵NX，其分布情况如图5(a)所示，其特征点主要集中于谐波带内，文献[6]即基于扬声器谐波带进行分析并得出检测结果，已经初步验证谐波带内有效信息较多。

图5 特征分布情况Fig.5 The distribution of feature points

式(9)中，Zx为谐波域特征点矩阵，NX为谐波带域模板矩阵。

应用式(10)提取其高次谐波特征点矩阵，并对高次谐波域做进一步分割；将其分割为左右共振区以及中间区域3部分，分布如图5(b)所示，特征点主要集中于共振区域。

式(10)中，Zg为高次谐波特征点矩阵，NG为高次谐波域模板矩阵。

2.3 检测模型建立

将上文所提取扬声器特征矩阵Z作为特征提取模板，对3 位专业声音检听员均认证合格的50 支扬声器进行特征提取，将所提取赋值特征点按其在矩阵中每列纵坐标从小到大的顺序进行排列，连接排列后特征点构建扬声器特征曲线；将50条合格扬声器特征曲线叠加，提取上下边界值得到如图6 所示合格扬声器特征曲线边界，并将其作为检测模型的检测域构建全特征点检测模块。若被测扬声器特征曲线超出检测域点数低于所设定最小阈值，如图7(a)所示，则判定该扬声器为合格产品；若超出检测域点数高于所设定最大阈值，如图7(b)所示，则判定该扬声器为异常声产品；否则判定为中间状态，需进一步处理。

图6 全检测域Fig.6 Complete detection area

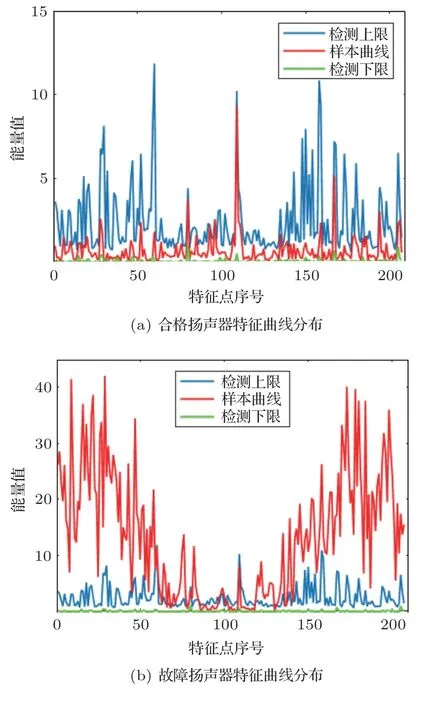
图7 全检测域特征曲线分布Fig.7 Feature curve distribution in the complete detection area

为进一步确定全特征点检测模块中结果为中间状态扬声器样本的合格性，应用全特征点检测模块的构建方法，依次对分割后的特征区域构建谐波带特征点检测模块、高次谐波左共振区特征点检测模块、高次谐波中间区域特征点检测模块以及高次谐波右共振区特征点检测模块。应用上述各模块依次对中间状态扬声器样本进行检测，其中任何模块判断该样本存在故障，即认定该扬声器存在异常声，经过多模块协同检测，可进一步提升检测系统检测精度。

本文将开胶(扬声器盆架与振膜的粘结不充分，导致发声时气压发生改变，造成扬声器异常声故障产生)、擦声圈(声圈与永磁场同心度误差较大，导致声圈往复运动时与场心柱发生擦碰，造成扬声器异常声故障产生)；小声(声圈的有效长度不足或永磁场强度较弱，导致系统额定阻抗增大，造成扬声器异常声故障产生)等扬声器时频特征点进行统计，对该类型故障扬声器专有特征点进行归类提取。选取上述3 种故障扬声器各10支，统计其专有特征点，用上文所述检测模型构建方法进行模型建立。图8(a)～(c)分别为开胶样本、擦声圈样本、小声样本在开胶故障专用检测模板中的分布情况，根据待测样本特征曲线在特征检测域的分布及超出检测域数量情况，确定扬声器故障原因。擦声圈及小声扬声器特征检测域也以此方法进行构建，不再赘述。

图8 开胶特征检测域Fig.8 Detection area of chip features

3 实验及结果分析

以图9 所示原理图搭建检测系统，采集所需数据并完成调试验证工作；在本实验系统中，每支待测扬声器样本仅需提取207 个特征点进行分析处理。先后对已知合格性的3 批某型号扬声器共676 支进行检测，扬声器样本属性如表1 所示，检测结果如表2所示。

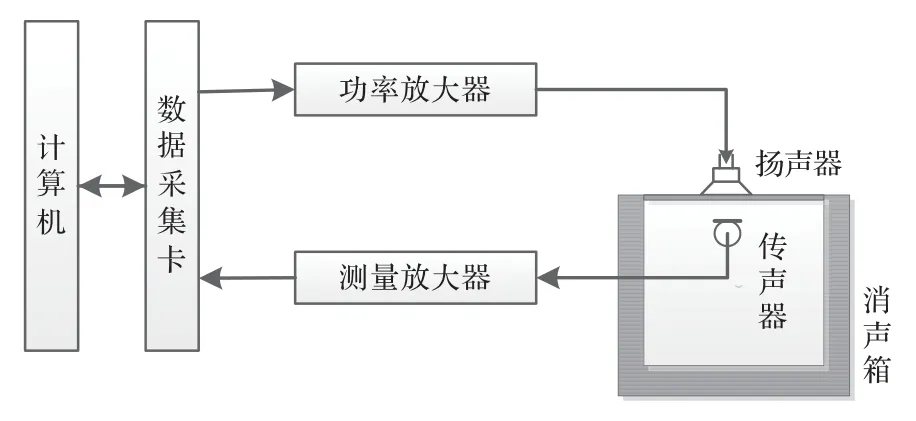
图9 实验检测原理图Fig.9 Schematic diagram of experimental measurement

表1 扬声器样本属性Table 1 Properties of loudspeakers

表2 检测结果Table 2 Detection result

表2 中合格样本误判：将合格扬声器判断为异常声产品；故障样本误判：将异常声扬声器判断为合格品；合格样本中间态：未判断出合格性的合格扬声器样本；故障样本中间态：未判断出合格性的异常声扬声器样本。

先后对某型号已知故障类型为开胶、擦声圈、小声以及未知故障类型扬声器各20 支进行分类检测，结果如表3所示。

由表1～2 可初步分析得出，对企业影响较大的异常声扬声器误判为合格品仅占0.15%，待进一步人工确定的中间态扬声器占比1.78%，有效检出率为97.63%，异常声检测效果明显。根据表3 检测结果可初步判定，本文所采用检测方法对扬声器异常声分类精度可达95%。

表3 分类检测结果Table 3 Classification detect result

结果分析：相较于文献[7]所述检测方法，检测449 支扬声器样本，中间态样本占182 支，有效检出率仅约60%；同样基于短时傅里叶变换所得时频图进行分析，本文所构建扬声器异常声检测模型对于异常声扬声器的有效检出率约97%，远高于文献[7]所述能量均值法；初步验证本文所述特征提取算法可降低短时傅里叶变换自身误差对检测系统的影响。对本实验中的误判扬声器样本进行了特征分析，发现其特征曲线仅有小部分特征点差异性较大，未达到系统设定检测阈值；其成因为检测模型构建过程中，对该类型异常声故障样本的特征提取较少，未能充分提取其异常声故障特征，造成检测过程中被误判为合格样本。文献[13]所述变分模态分解能量熵算法对于扬声器异常声故障的平均识别率为96.3%，而本文所述时频特征提取算法的识别率最高为95%，相较变分模态分解能量熵算法存在一定差距；其成因主要为基于短时傅里叶变换的时频分析法存在系统误差，本文所述特征提取算法虽进一步降低了其影响，但仍存在部分系统误差对检测系统识别精度的干扰。

4 结论

本文基于改进SIFT 算法对扬声器时频图提取特征点，分析处理后构建特征点法，并将其应用于扬声器异常声的检测。经过初步实验验证，可得出如下结论：

(1)特征点法可应用于扬声器异常声检测系统，并进行部分故障的分类。

(2)本系统在少量特征数据处理的情况下仍能获得预期检测效果。

(3)本文所述基于时频特征提取方法可在一定程度上降低短时傅里叶变换所产生系统误差对检测精度的影响。

本文所述方法仍需做大量验证实验，进一步确定本系统的检测精度及稳定性；本文所构建检测系统基于普通扬声器，对于低频扬声器的研究尚显不足，后续研究将进一步针对低频扬声器特征进行分析。