空调室外机钣金结构辐射噪声分析与优化

杜明龙 丛 辉 邓玉平 闫丽俊

(青岛海信日立空调系统有限公司 青岛 266510)

0 引言

空调室外机噪声大致分为结构噪声、电磁噪声、流体噪声，其中结构噪声包含摩擦噪声、碰撞噪声、共振辐射噪声，以低频周期性单峰值为主。低频噪声具有传播距离远、穿透性强的特点，极易从室外机透过墙体传递至室内，影响用户睡眠。针对低频共振噪声问题的声源定位与优化设计，振噪领域的学者做过大量研究，并形成相对成熟的理论与优化方法。刘林芽等[1]基于车辆-轨道耦合动力学模型，计算30 m简支槽型梁的振动响应，利用声传递向量法分析槽形梁结构各板件的低频噪声辐射贡献；张俊红等[2]采用折衷规划法和平均频率法相结合的方式对驾驶室整体刚度与四阶关键固有频率开展多目标形貌优化，使人耳处总声压级降低3 dB；李伟平等[3]对矿用自卸车驾驶室内部进行声振耦合分析与声学贡献量分析，针对声响贡献量最大的板件的四阶模态开展多目标形貌优化，有效地降低驾驶员右耳处的低频峰值。

参照多联机空调系统的国标GB/T 18837《多联式空调(热泵)机组》形成的企业标准，对某空调系统联机压缩机5280 r/min 运转时，距离机组1 m、(机组高度+1 m)/2 的高度位置处，176 Hz 频率下快速傅里叶变换(Fast Fourier transform, FFT)峰值为55.74 dB(A)，远大于基准值45 dB(A)，如图1所示。

图1 整机测点位置与400 Hz 以内频谱峰值Fig.1 Measured position of outdoor unit and spectrum of measured position within 400 Hz

本文基于两倍频振动发生原理，计算双转子压缩机吸排气过程中的转动力矩，施加在整机有限元模型中，计算室外机钣金框体的振动响应与钣金噪声辐射噪声的贡献量，确定两倍频噪声峰值高的主因，进而开展钣金压型的优化设计，降低整机的钣金共振辐射噪声峰值。

1 压缩机激励源确定

双转子制冷压缩机的激励力包含电磁力、气体力、液体力、机械力4 种，气缸周期性的完成吸气、压缩、排气和余隙膨胀4 个过程，产生压缩机旋转频率两倍的激振力矩[4]。气缸两倍频激振力矩引起压缩机本体以及连接吸排气管路的振动，吸排气管路振动传递至整机外围钣金，极易引起钣金共振，放大辐射出压缩机转速两倍频噪声。

根据双转子压缩机工作原理，计算气缸周期性的两倍频激振力矩。如图2 所示，AD与BC段圆弧压力相等，方向相反，相互抵消；AB段与CD段圆弧压力方向相反，大小不同，故单转子承受气体合力为[5]

图2 转子压缩机气缸力学原理图Fig.2 Dynamical schematic design of rotor compressor’s cylinder

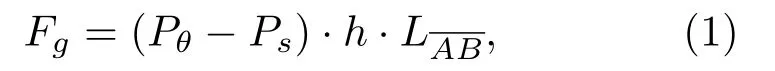
其中，Pθ为压缩机容积内压力，Ps为吸气压力，h为气缸高度，为AB长度；双转子压缩机的两个气缸相位相差180◦，双转子压缩冷媒的扭转力矩为

压缩机转动力矩随压缩机运转频率的变化曲线，如图3所示。

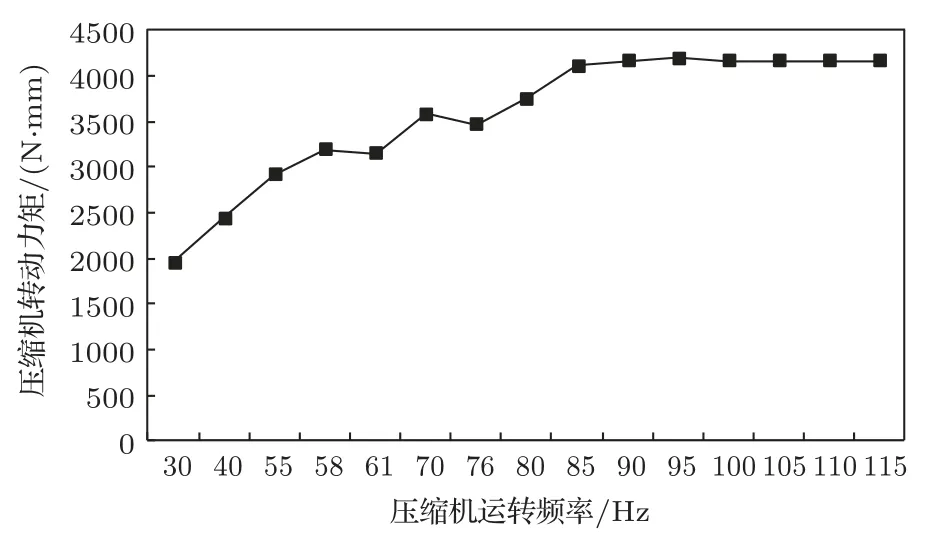
图3 压缩机转动力矩曲线Fig.3 Torque curve of compressor

2 钣金振动仿真

压缩机激振力通过铜管与底脚传递至空调室外机钣金，引起钣金共振并辐射噪声。获得压缩机两倍频扭矩后，施加在室外机空调系统整机有限元模型上，应用模态叠加法，进一步计算整机钣金的振动速度响应。

2.1 模态叠加法原理

空调整机铜管与钣金的结构阻尼小，任一点的响应均可表示为各阶模态响应的线性叠加，故采用模态叠加法计算外围钣金的频率响应。整机有限元模型假设为N个自由度系统，得到动力学公式为[6]

其中，[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{f}为激振力矩向量；{x}为位移响应向量。模态向量矩阵[Φ]求解后，系统节点的位移响应可以表示为[7]

应用特征向量间的正交性，式(3)转化为

其中，[Mp]、[Cp]、[Kp]称为模态质量矩阵、模态阻尼矩阵、模态刚度矩阵，均为对角阵。将式(11)与式(7)联立，求解出各节点在激振力矩{f}下的位移响应。

2.2 钣金模态测试与振动响应计算

应用LMS Test.lab 测试系统对整机框体开展模态测试，确定整机钣金框体在175.3 Hz 附近存在明显共振(如图4 所示)。建立整机有限元仿真模型，在压缩机本体气缸中心位置处施加绕压缩机本体中心轴的转动力矩，具体数值见图3。钣金结构阻尼设置为0.05，应用模态叠加法计算整机的振动频率响应发现：172 Hz下的振动位移响应最大(如图5所示)，振型与模态测试结果相符。通过模态测试与整机频响计算结果对比，明确整机压缩机5280 r/min运转时两倍频大主要是外围钣金框体共振引起的，且计算频率偏差约3 Hz，计算精度满足进一步开展各部件的声学贡献量分析的要求。

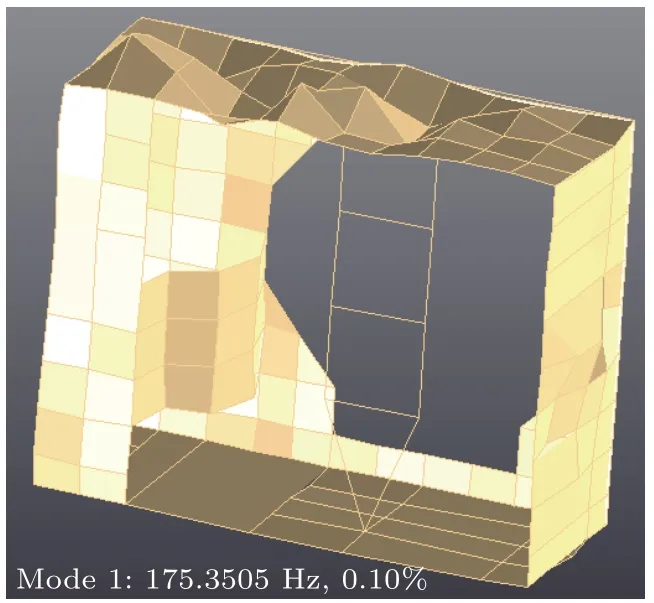
图4 整机175.3 Hz 下的模态振型Fig.4 Modal shape of outdoor unit at 175.3 Hz

图5 整机172 Hz 下的位移频率响应云图Fig.5 Displacement contour of outdoor unit at 172 Hz

3 钣金辐射噪声贡献量分析

基于整机频率响应计算结果，应用间接边界元法，开展噪声测点位置处噪声贡献量分析，确定两倍频噪声的传递路径，明确两倍频的发声位置，定位声源。

3.1 间接边界元理论

假设在无限声场中结构辐射噪声为小振幅波动且为线性，根据Neumann边界条件、Sommerfield辐射条件，可得Helmholtz边界计分方程[8−9]：

间接边界元的网格可以为非封闭且同时计算内声场与外声场，间接边界元的方程为

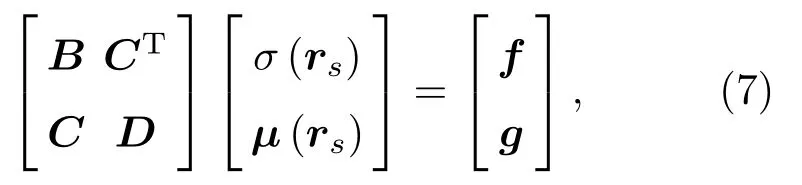
式(7)中，B、D为系数矩阵；C为耦合矩阵，f与g为激励向量。

求解出σ(rs)与µ(rs)并代入式(6)，可得到辐射声场中任意点的声压为

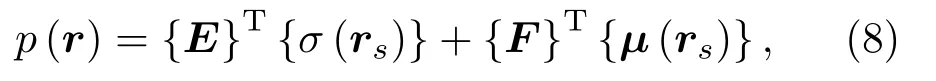
其中，{E}与{F}为系数向量。

3.2 声学传递向量理论(ATV)

声学传递法在线性声学假设的前提下，建立边界元网格与声场测点处的固有联系，仅与结构的几何形状、测点位置、声波频率和声介质有关。在辐射声源的频率范围内，测点位置处的声压可以表示为[1,10]

其中，r为测点位置位矢；υn(ω)为结构表面法向振速；ω为角频率；ATV(ω)为声传递向量，可表示为ATV(ω)=[C]T[A]−1[B]+[D]T，矩阵中各元素可以表示为

式(10)中，Sα、Sβ、Sγ与Si表示离散单元；rα、rβ、rγ与ri是单元位置位矢；G为自由格林函数；Ni为单元形函数；ρ为介质密度；δαβ为Kronecher符号。

3.3 钣金贡献量计算

钣金框体为跨度大的薄板结构，在振动激励下极易共振，放大辐射共振噪声，故需开展钣金框体不同位置对测点噪声的贡献量，确定172 Hz 异常噪声的发声部位，开展有针对性的局部优化设计，消除局部共振辐射噪声。将2.2 节的钣金框体频响计算结果，导入声学仿真软件中，钣金框体离散成6个单元组：前面板、中隔板、背板、上盖、底板、侧盖，如图6所示。

图6 钣金框体声学离散示意图Fig.6 Acoustic grids diagram of the metal shell

基于间接边界元法，计算每个单元组至测点位置处在172 Hz 频率下的声学贡献量：背板、中隔板、前面板的贡献量远大于侧盖、上盖、底板，如图7 所示。因此，整机172 Hz 异常峰值由背板、中隔板、前面板共振引起。

图7 间接边界元法声学贡献量计算结果Fig.7 Calculated result of acoustic contribution using the indirect boundary element

4 改善设计与验证

4.1 背板凸包形状优化设计

背板为薄板类结构件，采用全封闭设计，腹板结构表面辐射声功率与质点振动速度的关系[11]为

式(11)中：σ为声辐射效率；ρc为介质特性阻抗；S为背板振动表面积为背板振动速度均方值的平均值。由式(11)知，背板辐射噪声与表面振动速度强相关，故使用商用软件的形貌优化技术，使背板结构第一阶固有频率最大，防止背板在压缩机运转频率内共振，降低背板的振动速度，从而降低低频共振辐射噪声。

设计变量：

目标函数：

约束条件：

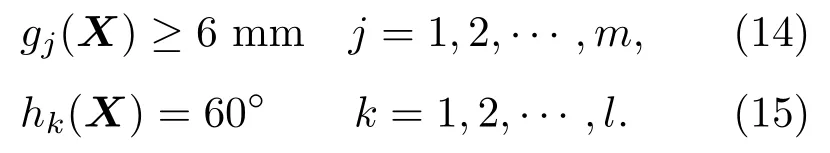
设计变量为节点沿背板设计区域单元法向扰动的形变量，形变量为直径为最小筋宽的圆形区域，0 ≤xi≤3 mm；目标函数为第一阶固有频率f1最大；g(X)为最小筋宽≥6 mm；h(X)为起筋角度为60◦。背板设计变量的位置见图8 蓝色区域，设计变量与约束条件数学模型的示意如图9所示。

图8 设计变量位置示意图Fig.8 Diagram of design variable’s position

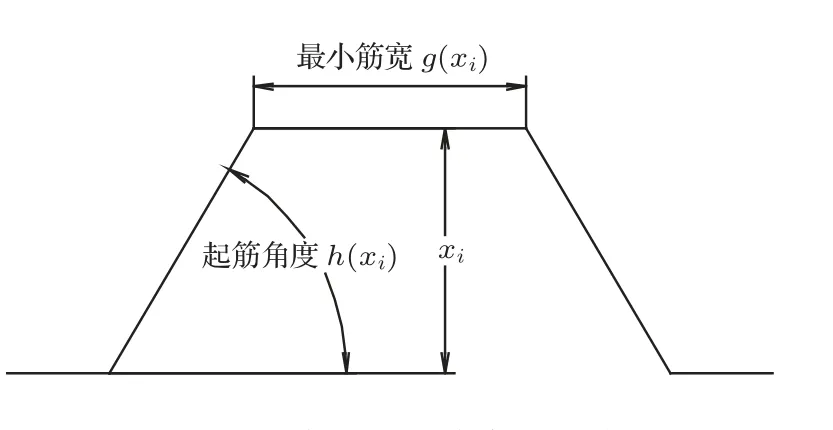
图9 设计变量与约束条件示意图Fig.9 Diagram of design variables and constraint conditions

由图10所示，背板经过11 次优化迭代后，第一阶固有频率收敛至201.5 Hz，远大于压缩机运转上限频率(最大转速：5400 r/min)的两倍频转动力矩振动频率180 Hz，可有效地改善背板共振问题。背板凸包形状的优化结果如图11(a)所示，在云图的红色与黄色区域内设计3 mm 高度的凸包，绘制三维模型，最终优化方案如图11(b)所示。

图10 固有频率优化收敛历程图Fig.10 Optimization convergence process

图11 背板形貌优化结果与三维模型Fig.11 Topography optimization result of natural frequency and 3D model of the back plate

4.2 前面板与中隔板改善措施

(1)针对前面板的局部共振问题，基于经验在前面板局部共振的4 个角落处，分别增加4 个凸包压型，压型高度为2 mm，压型位置与形状见图12，避免前面板4个角位置处局部共振。

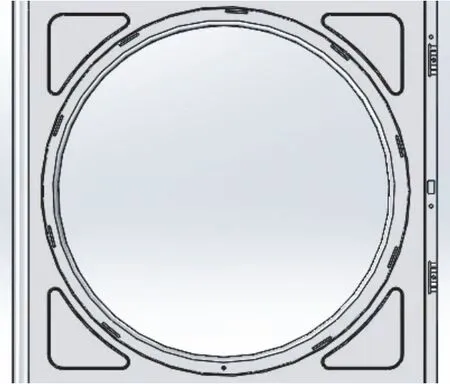
图12 前面板凸包压型示意图Fig.12 The beads diagram of the front panel

(2)中隔板的压型构造复杂，且安装冷媒循环系统元器件，故仅在中隔板的整个背部面贴附2 mm 阻尼材料溴代丁基橡胶，利用阻尼材料的黏弹性，降低中隔板直接向整机背部的辐射噪声。

4.3 整机噪声试验验证

应用背板、前面板、中隔板的改善措施，搭建实验样机，开展整机噪声实验验证，测试400 Hz 以内的频谱(如图13所示)发现：优化后整机异常两倍频明显改善，176 Hz频率下的噪声峰值从55.74 dB(A)降低至45.11 dB(A)，峰值减小10 dB(A)左右。

图13 钣金框体优化前后频谱对比图Fig.13 Spectrum comparison of before and after optimization of metal shell

5 结论

本文针对空调室外机在5280 r/min 转速下两倍频异常高的问题，建立双转子压缩机吸排气两倍频扭转力矩的计算模型，获得不同压缩机频率下两倍频的激振力矩；基于模态线性叠加法，建立室外机整机的有限元模型，施加两倍频扭转力矩，计算钣金框体的频率响应，经过整机钣金框体模态测试校核，确定整机两倍频高是钣金共振引起的；将钣金框体的频响结果导入声学仿真软件，应用间接边界元法计算框体各部位相对于测点的贡献量，确定背板与中隔板共振；基于形貌优化技术，优化背板的压型，同时中隔板共振局部位置贴附阻尼，使两倍频异常峰值从55.74 dB(A)降低至45.11 dB(A)，有效地改善钣金辐射的“嗡嗡”噪声。后续可在激励源提取、整机振动频率响应仿真、间接边界元仿真环节深入开展模型校核，提高计算工作的精度。