Nonlocal nonreciprocal optomechanical circulator

Ji-Hui Zheng(郑继会) Rui Peng(彭蕊) Jiong Cheng(程泂)Jing An(安静) and Wen-Zhao Zhang(张闻钊)

1School of Mathematical Sciences,Guizhou Normal University,Guiyang 550025,China

2School of Physical Science and Technology,Ningbo University,Ningbo 315211,China

3School of Physics,Dalian University of Technology,Dalian 116024,China

Keywords: optomechanics,nonlocality,nonreciprocity

1. Introduction

Nonreciprocal quantum state transmission has emerged as an indispensable tool for the important applications in quantum information processing such as optical diode,[1–3]noisefree sensing,[4]unidirectional amplifier,[5]and nonreciprocal phase shifter.[6]A nonreciprocal response can be generated by direct breaking of the time-reversal symmetry in the transmission. Many protocols have been proposed in both theoretical and experimental perspectives to achieve this propose.In the electromagnetic domain, special magnetic effects are explored and widely used for nonreciprocal response.[7–9]In the optical domain, directional transmission of light has been achieved with optical nonlinearities or dynamically modulated media.[10,11]In the atomic domain,nonreciprocal cyclic transition has been proposed in a multi-level atomic system or topological cold-atom systems.[12–14]Nonreciprocal effects have been exported in many typical quantum systems. Corresponding applications have been reported to realize quantum device based on the nonreciprocal response.

Hybrid quantum operations are usually used to optimize or implement multiple quantum processing. Recently,nonreciprocal transmission in optomechanical system has attracted more and more attention for its potential applications in hybrid quantum system and hybrid quantum network.[15–17]The optomechanical system was referred to as a natural bridge between photons and phonons.[18]Thus, the controlling and transmission between solid state and flying state are subsequently realized in such system. For example,nonreciprocal phonon transport based on arrays of optomechanical microtoroids,[19]nonreciprocal conversion between microwave and optical photons in electro-optomechanical systems[20]and unidirectional amplification in optical gain optomechanical systems.[5]Up to now, most of the studies are limited in the localized quantum effect to achieve nonreciprocal properties. Nonlocality, as a distinguishing feature of quantum mechanics from classical physics, remains unexplored when studying the quantum nonreciprocal effect in optomechanical systems. Therefore, it is necessary to find that if the nonlocal manipulation of nonreciprocal transmissions could be achieved in optomechanical systems.

Remote transmission or distribution of optical quantum state has been well studied in optical fiber and free space,[21]such as satellite-based entanglement distribution with longdistance,[22]and nonlocal quantum state transmission in optical fiber,[23]etc. The construction of quantum nonlocality based on this technology has been widely reported. Thus,it is possible for us to realize nonlocal interaction in optomechanical systems by utilizing the remote quantum technique. In this work, a scheme to achieve nonlocal nonreciprocal transmission is proposed in composite optomechanical systems. A nonlocal interaction is constructed between the remote optical and two mechanical modes. The time-reversal symmetry breaking is achieved through the nonlocal interaction of three bodies, so as to realize the nonlocal one-way quantum state transmission and control between optical and mechanical modes. This paper is organized as follows. In Section 2,we analyze the model and Hamiltonian according to the dynamic properties of the system. Using the linearization approximation and adiabatic elimination method, we obtain the nonlocal effective Hamiltonian, which is used to describe the long-range interaction between optical mode and two mechanical modes. We then study the optomechanical circulator behavior in Section 3. Eventually, discussions and conclusions are given in Section 4.

2. Model and Hamiltonian

As shown in Fig.1, the system consists of three parts: a composite optomechanical system,a empty cavity and a longrange lossless optical fiber (or free space). The long-range lossless optical fiber is used to transmit the output photons from cavity 1 to 2. The Hamiltonian of the system is written as

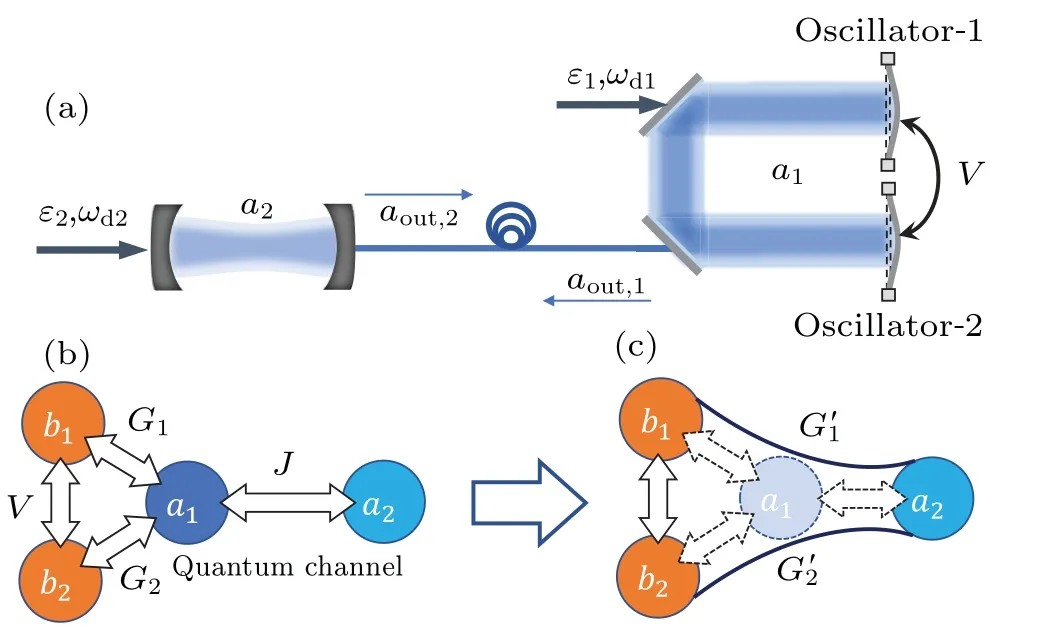
Fig. 1. (a) The schematic diagram of a nonreciprocal optomechanical circulator system. The monochromatic cavity field is coupled with two movable mirrors. Lossless fiber(or free space)is used to construct quantum channel between optomechanical cavity and empty cavity. (b)The interaction structure diagram of the system and the nonlocal interaction diagram we expected.

When this kind of resource is exhausted (when the correlation between photons disappears),we need to redistribute the nonlocal correlation photons. Thus,our protocol needs to have a correlation distribution process similar to entanglement distribution to maintain nonlocal and nonreciprocal transmission.

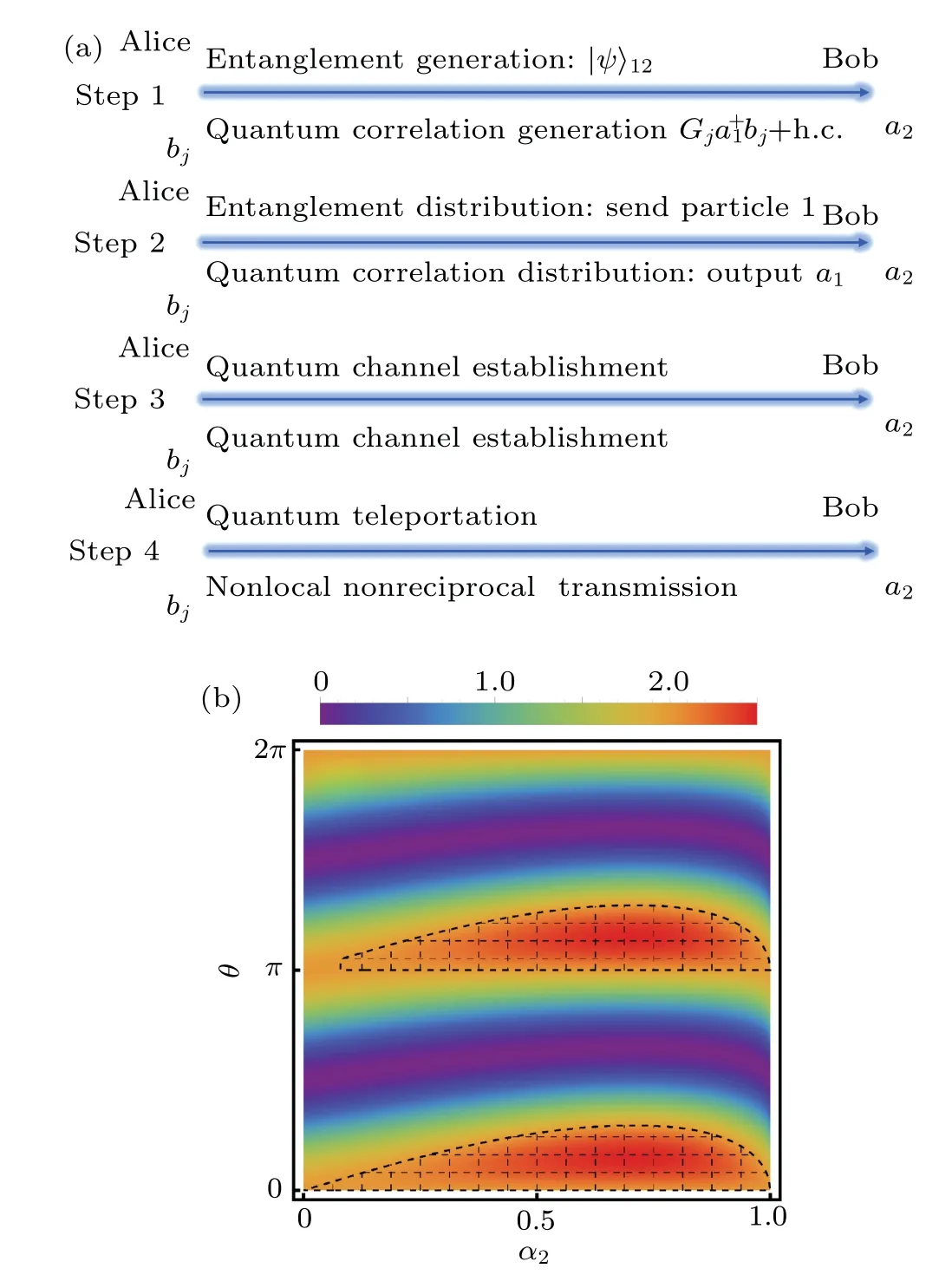
Fig. 2. (a) The step analogy between quantum teleportation and nonlocal nonreciprocal transmission, where the lower part of the line represents our protocol. (b)The average value of Bell-CHSH operator for continuous variable(CV)systems(|〈BCHSH〉|)as a function of angle θ and superposition coefficient α2. The black grid region represents the violation of Bell-CHSH inequality, that is, the parameters region with|〈BCHSH〉|＞2.

Under strong driving and weak coupling condition, the so called“linearized approximation”[18]is used to decompose the operator into average value and its fluctuation term, i.e.,ˆaj=αj+δˆaj,ˆbj=βj+δˆbj,whereαj ≡〈ˆaj〉is the mean values of ˆaj,andβj ≡〈ˆbj〉is the mean values of ˆbj,respectively.After choosing the suitable sideband withΔ′c1≈ωmj,the linearized Langevin equations of the system under the rotatingwave approximation are then governed by

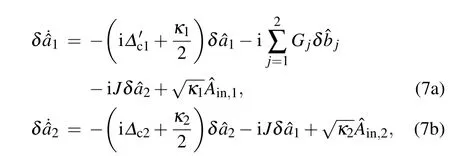
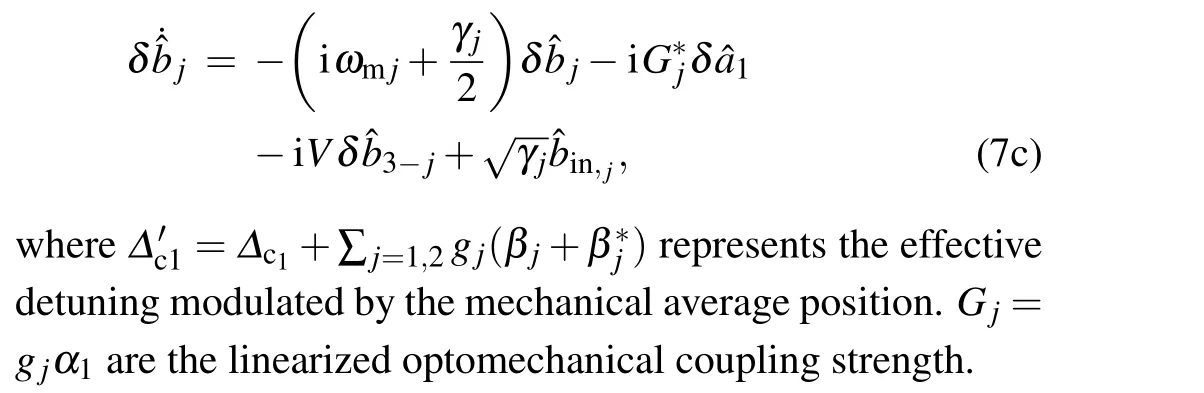
The interaction relationship diagram in the system is displayed in Fig. 1(b). We aim to eliminate the optical modeδˆa1, so as to realize the long-range interaction between optical modeδˆa2and mechanical modes, i.e., Fig. 1(c). Setting the strong dissipation of the optomechanical cavity, we can regard that the optical modela1is fast dissipative in the evolution of the system. Thus,the rapid dissipation modea1can be eliminated under the conditionκ1≫{γ1,γ2,κ2}. This method has been reported and confirmed in Refs.[25,26]. In this case,the nonlocal interaction between the optical modeδˆa2and the mechanical modes are obtained.This effective three-mode optomechanical system can be used as a three-port circulator[27]for one optical mode and two mechanical modes. The corresponding effective Langevin equations are (details are shown in Appendix A)

It is obvious that the effective parameters strongly depend on the above correction coefficient. Moreover, as long as we select the appropriate sideband,the amplified effective parameters can be obtained. In addition,under appropriate parameter conditions, we can write back the effective Hamiltonian according to the effective Langevin equations (see appendix A for details discussion). This effective dynamics or Hamiltonian can provide us with a powerful means to further confirm that our scheme is nonlocal,and the Bell-CHSH inequality for continuous variable systems is tested.[28,29]Under the sideband condition, the average value ofBCHSHon Fock state is expressed as(details see Appendix B)

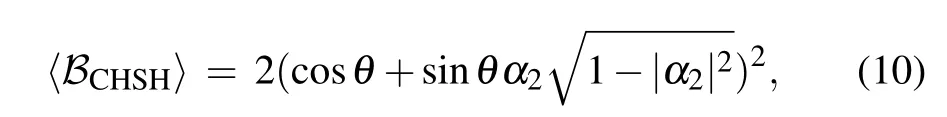
whereθa=θb=θdenotes the angles of unit vectors used to verify the inequality, andα2represents the superposition coefficients of the initial uncoupled states in the final state after evolution. WhenG′j=0,the coefficientα2=1,the maximum value of〈BCHSH〉is 2, which does not violate Bell-CHSH inequality, and the system embodies locality. The nonlocality of our system will be confirmed as long as the inequality|〈BCHSH〉|≤2 is violated. In black grid region in Fig.2(b),the results show that|〈BCHSH〉|＞2. The violation of the inequality here depends onG′jin Eq.(9),that is,the remote interaction strength mentioned in our previous analysis.

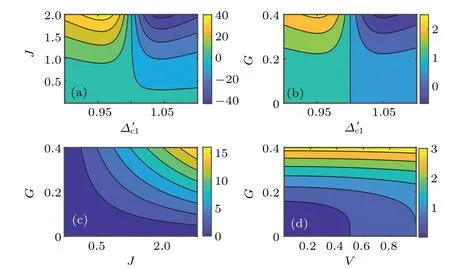
Fig. 3. The effective parameters Δeff, ωeff, G′j,Vj as a function of the original parameters J, Δ′c, G,V (units of ω-1m ). Other parameters are γ=10-3ωm,κ1=10κ2=ωm/10,Δc2=ωm and Δ′c1-Δc2=10-4ωm.

As shown in Fig. 3, the dependence of the effective parametersΔeff,ωeffj,G′jandVjon the original parameters are displayed in the sub-figures (a), (b), (c) and (d), respectively.For the convenience of discussion, we setωmj=ωm,γj=γand|Gj|=G. Figure 3(a)shows the effective detuning as the function ofΔcandJ. It is obvious that,Δeffcan be adjusted from-40ωmto 40ωmwith small original parameters change,i.e.,J/ωm∈[0,2]andΔ′c1/ωm∈[0.9,1.1]. Other effective parametersωeffj,G′jandVjcan also be adjusted in a large range with the small change of the original parameters{G,J,Δ′c1,V}.The corresponding results are shown in the sub-figures(b),(c)and(d),respectively.

According to the expression of Eq.(9),the effective dissipation coefficientκeffandγeffare modulated by the original parameters. Therefore, when we use the original parameters to enhance the coupling rate, the effect of dissipation should also be taken into account. The relationship between effective dissipation and coupling coefficient are shown in Fig. 4.The effective dissipation increases with the increase of coupling coefficientsJandG. In the following discussion, we will consider both the enhancement of effective coupling and the change of effective dissipation from the original parameters.

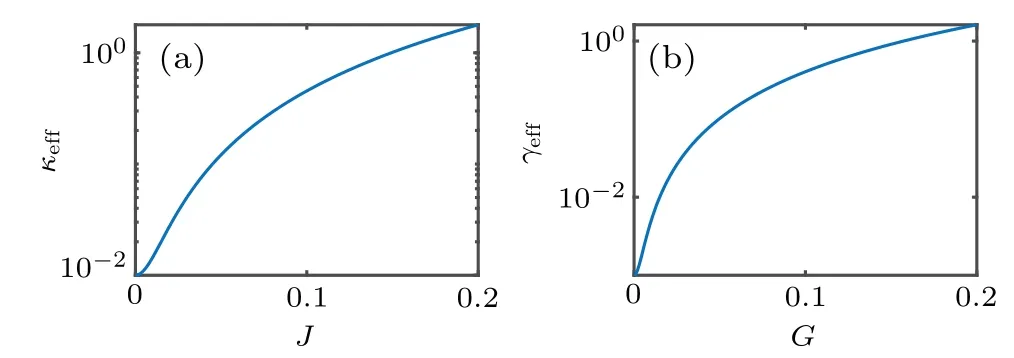
Fig. 4. The effective dissipation coefficient (a) κeff and (b) γeff as a function of the original parameters J,G. Other parameters are the same with Fig.3.

3. Nonlocal circulator

In this section, we mainly study how to realize the nonreciprocal transmission of photon-phonon in the three mode nonlocal optomechanical system. Perfect nonreciprocal transmission means that signals can be transmitted completely from one side of the system to the other while blocking reverse transmission. To achieve this nonreciprocal transmission, we characterize the input–output relations of such a device and shows the adjustability of the system.For simplicity,the above Heisenberg–Langevin Eq.(8)is written in compact form as

whereSvacdenotes the output spectrum contributing from the input vacuum field. Under rotating wave approximation,Svaccan be ignored. The corresponding scattering matrixTthen is expressed as

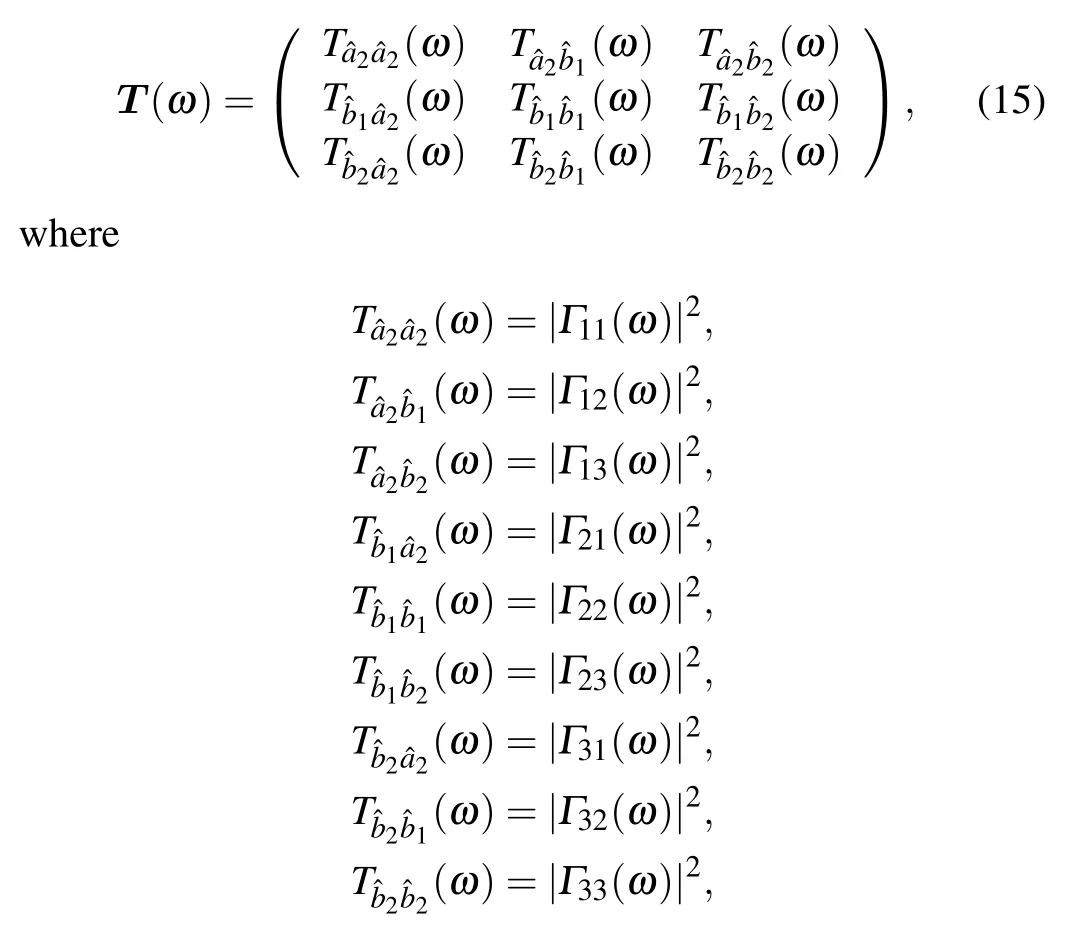
whileTx,ydenotes the transmission rate from modexto modey. In the aspect of experimental simulation,we generally pay more attention to the adjustable parameters in the experiment.We noticed that modesb1andb2are completely symmetric in the form of dynamics. Therefore,when considering the influence of parameters, we only need to pay attention to the parameters of one of the modes.

The effective coupling rateG′jandVjare complex, and without lose of generality,we can setG′j=Gj0exp(-iθj)andVj=V0exp[(-1)jiθ3]. The phases of the coupling rate plays an important role in nonreciprocal transmission,which can introduce a symmetry breaking of the system modes coupling and then to achieve nonreciprocal transmission. The corresponding effective of the phase factorθ1on the max value ofTˆa2ˆb1(ω)and min value ofTˆb1ˆa2(ω)is displayed in Fig.5.

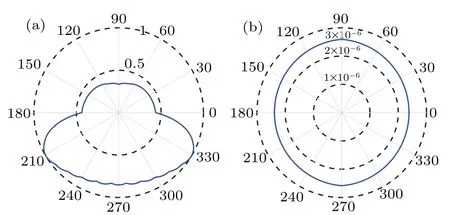
Fig. 5. The transmission rate Max[Tˆa2 ˆb1(ω)] and Min[Tˆb1 ˆa2(ω)] as a function of the phase factor θ1 (rad). Other parameters are the same with Fig.3.

As shown in Fig. 5(a), it is obvious that the phase factor has a significant influence on the maxmal transmission rateTˆa2ˆb1(ω). The maximum value of the transmission rate can reach 1 when the appropriate phase factor is selected. According to the figure,Max[Tˆa2ˆb1(ω)]=1 are reached around 210°and 330°. In Fig. 5(b), the influence of phase factor on minimal value ofTˆb1ˆa2(ω) can be ignored. For any value ofθ1,Min[Tˆb1ˆa2(ω)] is closed to zero, that is, phase has not affect on the block ofTˆb1ˆa2transmission. To achieve nonreciprocity,it is necessary to select appropriate parameters to achieveTˆa2ˆb1≈1 andTˆb1ˆa2≈0 at the sameω.

To further discuss the nonreciprocity effect in our protocol, we show the relationship of transmission rate Max[Tˆa2ˆb1(ω)]and adjustable parameters:θ1,θ3,G10andV0.The corresponding results are displayed in Fig. 6. As shown in Fig. 6(a), the maximum transmission rateθ1andθ3on Max[Tˆa2ˆb1(ω)] increases and decreases periodically with the increase ofθ1andθ3. When the values ofθ1andθ3meet the appropriate matching conditions,that is,the bright yellow region in the figure,the maximum transmission rate is close to 1.As shown in Fig.6(b), we investigate the influence ofθ1andG10on the maximum transmission rate.It is obvious that whenG10is large enough, no matter what the phase factor is, we have Max[Tˆa2ˆb1(ω)]=1. According to the effective Langevin Eq.(7a),G10represents the coupling strength between the optical mode ˆa2and the mechanical mode ˆb1,which directly determines the information transmission ability between this two modes. WhenG10≫{G20,V0},the coupling between ˆa2and ˆb1is dominant in the system, and under this condition, the system can be approximated as a two-body interaction system. The interaction of our system shows a symmetrical structure,thus the phase modulation effect is suppressed. Although the maximum transmission rateTˆa2ˆb1can be achieved,nonreciprocity effect will disappear. When the value ofG10is close to{G20,V0},the system is a three body circulator. Under this condition, the influence of phase factor is highlighted. There are obvious extremums ofθ1around 7/6πand 11/6π. As shown in Fig. 6(c), whenV0is large enough, no matter what the phase factor is,we have Min[Tˆa2ˆb1(ω)]≈0. This is due to the symmetry of the dominant coupling of ˆb1and ˆb2. WhenV0≫{G10,G20}, the coupling between ˆa2and ˆb1can be ignored. When the value ofV0is close to{G10,G20},under this condition, the influence of phase factor is highlighted. There are obvious extremums ofθ3around 7/6πand 11/6π. Therefore,choosing appropriate parameters can realize and control nonreciprocity. To realize the three body circulator,the chose of the coupling rateV0andGj0should be closed. And the phase of the coupling rate also needs to meet the matching conditions.

Fig.6. The transmission rate Max[Tˆa2 ˆb1(ω)]as a function of the coupling parameters θ1,θ3,G10 and V0. Other parameters are the same with Fig.3.

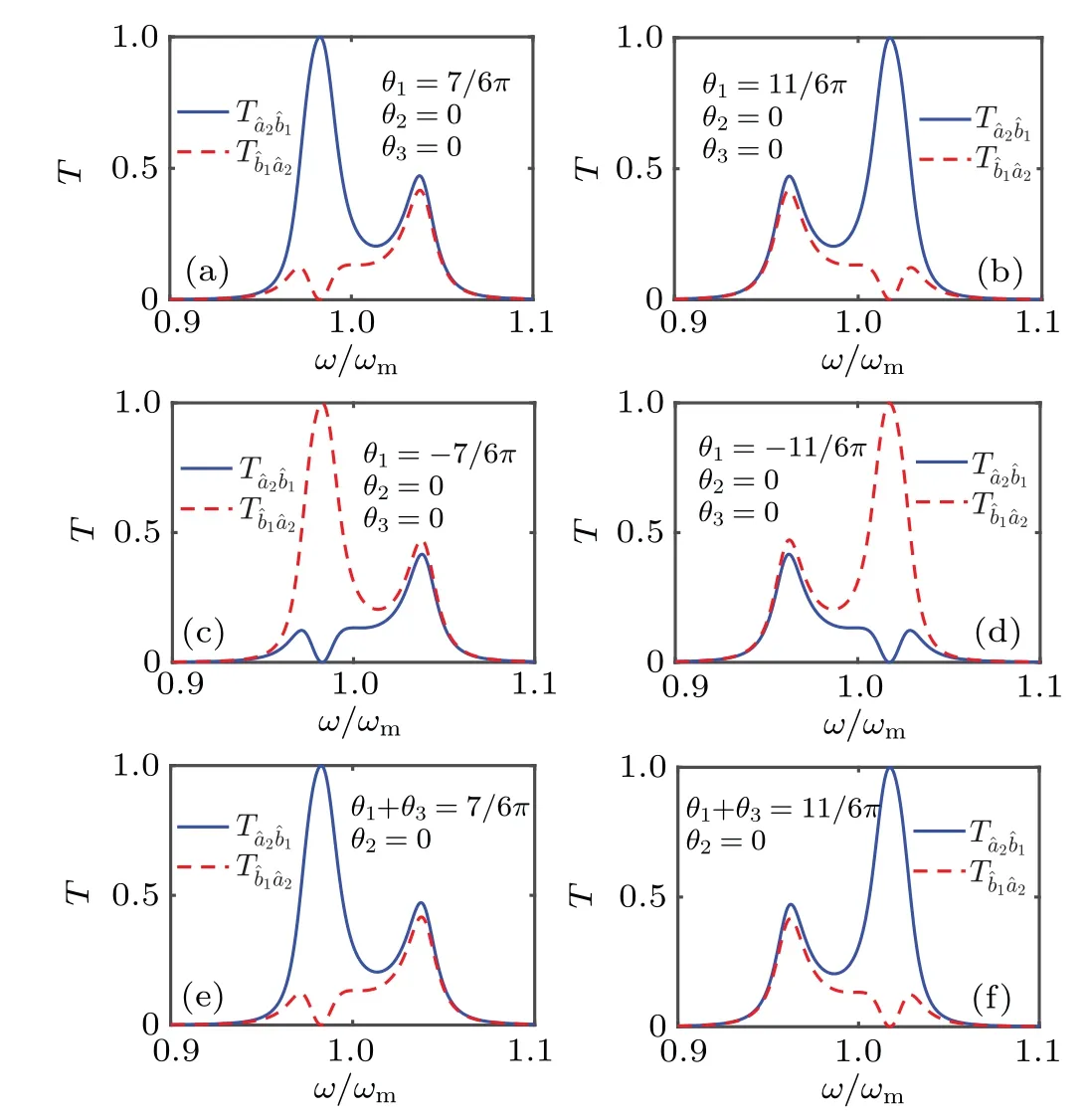
Fig. 7. The transmission spectrum with different phase factors. Other parameters are the same with Fig.3.

In stand three body circulator, the signal is transferred from one mode to another in either a counterclockwise(ˆa2→ˆb1→ˆb2→ˆa2)or clockwise direction,depending on the relative phase.[27]In our model, according to the conclusion in Fig.5,this relative phaseθ=7π/6 orθ=11π/6. As shown in Figs.7(a)–7(f),under the condition of phase matching,our system shows obvious nonreciprocity. This is consistent with the conclusions of our previous analysis.In Figs.7(e)and 7(f),we show that the selection of each phase can be arbitrary, as long as the phase accumulation on the circulator satisfies the condition. In the above process of nonreciprocal transmission,the transmission and reflection coefficient of the system itself is for the input signal. The input signal here includes both the signal that we want to transmit and the thermal noise. If the temperature of the environment is high, the proportion of information in the corresponding input signal will be low. In the transmission process of the system when the transmission coefficientT=1,the actual signal transmission coefficient will be greatly reduced due to the reduction of the signal ratio in noised input signal. Therefore, in order to improve the transmission rate of the signal, we need to lower the temperature.Conversely, ifT=0, the system will indiscriminately isolate both the signal and the input environment noise. The whole system is robust to temperature. This robustness is certainly not unlimited, because our calculation is based on the asymmetric property of the quantum correlation of the system, so this robustness is also built on the premise of not destroying the quantum property of the system.

4. Discussion and conclusions

A nonlocal three body interaction is constructed in hybrid optomechanical systems. Based on our nonlocal interaction system,we can build a nonlocal photon-phonon circulator and realize the quantum control of nonlocal optical mode to mechanical mode. As long as we let the accumulated phase reach a specific value, that is,θ=±7π/6 orθ=±11π/6, we can realize the nonlocal nonreciprocal transmission between the mechanical state and the optical state. In addition, the coupling coefficient between systems can be used to control or regulate the nonreciprocity of the system. For the effective coupling coefficientsV0andGj0, we can control the nonreciprocity by controlling the adjustable parameters,that is,the laser strengthεjdriving or detuningωdj. The corresponding relationship and controlling results are shown in Eq. (9) and Fig. 6, respectively. It is worth noting that, in the hypothesis of lossless fiber (or free space) in our scheme, we ignore the influence of environmental dissipation in the transmission process,and only consider the input noise of the optical cavity.If the dissipation of the transmission process is taken into account,it will inevitably introduce more noise,and one needs to add transmission noise to the expression for ˆAin. Fortunately,this noise is also similar to the input noise of optical cavity,which are uncorrelated noises,and the effect of the two noises on dynamical evolution is consistent.So we can combine them together,and the dissipation coefficient and noise are certainly greater than the lossless condition.

For the feasibility of our scheme,the optomechanical system of various frequency bands has been realized in experiments. The parameters used in our protocol can be easily implemented in typical micro-[31,32]or nano-[33,34]optomechanical systems withκ/ωm→0.1. Low loss remote optical transmission is realized in optical fiber or free space.[21,35,36]Therefore, our protocol provides an executable platform for the implementation of nonlocal and nonreciprocal phononphoton transmission or control, and eventually provides the basis for applications on quantum information processing or quantum networking.

Acknowledgments

We thank Rui-Jie Xiao and Yang Zhang for instructive discussions.

Project supported by the National Natural Science Foundation of China(Grant Nos.12061023,12074206,11704026,11704205,11704042,and 11847128)and K.C.Wong Magna Fund in Ningbo University,China.