Pressure-induced phase transitions in the ZrXY (X =Si,Ge,Sn;Y =S,Se,Te)family compounds

Qun Chen(陈群) Juefei Wu(吴珏霏) Tong Chen(陈统) Xiaomeng Wang(王晓梦) Chi Ding(丁弛)Tianheng Huang(黄天衡) Qing Lu(鲁清) and Jian Sun(孙建)

1National Laboratory of Solid State Microstructures,School of Physics and Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China

2Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100230,China

Keywords: high pressure, ZrXY (X = Si, Ge, Sn; Y = S, Se, Te) family, phase transition, superconducting temperature

1. Introduction

Topological semimetals (TSMs) with nontrivial band structures have been extensively studied due to their exotic properties, such as large magnetoresistance,[1—7]high charge carrier mobility,[1—7]and potential topological superconductivity.[8—11]Based on the degeneracy of the band crossing points and their distribution in the Brillouin zone, these TSMs can be classified as Dirac semimetals,[12—15]Weyl semimetals,[1,3,5,16—21]topological nodal-line semimetals,[22—29]etc. The band crossing points of Dirac semimetals are fourfold degenerate, while Weyl semimetals have doubly degenerated band crossing points.For topological nodal-line semimetals, the band crossing points create closed loops instead of separated points in the Brillouin zone. Among topological materials, ZrXY(X= Si, Ge, Sn;Y= S, Se, Te) has been studied intensively.[24,30—46]Materials of the ZrXYfamily usually host two types of Dirac states,i.e., the nodal-line state doubly protected by mirror and inversion symmetry and the two-dimensional (2D) Dirac state protected by nonsymmorphic symmetry. In addition,different members have diversified properties. For instance, ZrSiS has a large, anisotropic magnetoresistance, which can be as high as 1.4×105%at 2 K and 9 T.[47]

On the other hand, pressure plays an important role in the phase transition of matter. It provides an easy and clean way to force a structural transition of materials without contamination by impurities,[48—50]and provides an effective way of synthesizing new materials.[51]Pressure-driven structural phase transitions are often accompanied by variations in electronic structures,resulting in different physical properties. For instance,pressure has been successfully adopted to induce superconductivity in topological materials[10,52]and phase transitions with new topological properties.[53]ZrXYfamily members also have novel properties under high pressure. For instance, ZrSiS was found to have lattice distortion induced by inhomogeneous compression under nonuniform hydrostatic pressure,[40]and ZrSiTe was found to have a drastic change in the electronic band structure under pressure.[54]

However, the existing works on the ZrXYfamily have been performed at relatively low pressure. Here, we systematically studied the entire ZrXYfamily,includingX=Si,Ge,Sn andY= S, Se, Te, and extended the pressure range up to 200 GPa. We found several new phases and then studied their electronic and superconducting properties. For instance,ZrGeS undergoes an isosymmetric phase transition from the ambientP4/nmmstructure to a newP4/nmm-II phase. In addition, we also found a new phase called theP4/mmmphase.Remarkably, the phonon dispersion calculation results show that theP4/mmmphase of ZrGeSe and theP4/nmm-II phase of ZrGeS may be quenchable to ambient pressure. Interestingly, the estimated superconducting critical temperatures(Tc)ofP4/mmm-ZrGeSe andP4/nmm-II-ZrGeS are 8.1 K and 8.0 K at 0 GPa,respectively.

2. Computational method

We used the machine-learning and graph theory accelerated structure searching(Magus)code[55,56]combined withab initiocalculations to search for the stable structures of ZrXYat 50 GPa,100 GPa,150 GPa,200 GPa. The Magus code has demonstrated success in predicting the high-pressure structures of various systems.[50,51,57]We performed structure optimizations and calculations of enthalpy,mechanical properties,and electronic structures using the projector augmented wave(PAW)[58]method in the Viennaab initiosimulation package(VASP)[59]and the Perdew—Burke—Ernzerhof (PBE)[60]generalized gradient approximation(GGA)exchange—correlation density functional. Electronic localization functions (ELF)calculated by VASP were displayed by visualization for electronic structural analysis (VESTA).[61]Structures were relaxed with a high accuracy plane-wave basis energy cutoff of 400 eV. Thek-mesh spacing of Brillouin zone is 2π×0.025 °A-1. Phonon modes and frequencies of the structures were calculated by the finite displacement method implemented in the PHONOPY[62]code. The elastic constants were determined by the linear-response stress—strain method,as implemented in the VASP code, and the bulk and shear moduli were calculated based on Voigt averaging.[63]The Vickers hardness was computed by the model of Chenet al.[64]We applied a 2×2×2 supercell to calculate the force constants of all structures. Quantum Espresso (QE) code[65]was used to calculate the electron—phonon coupling constants andTcusing an energy cutoff of 120 Ry. The surface states were obtained by constructing the maximally localized Wannier functions[66]and using the surface Green function approach,[67]as implemented in the WANNIERTOOLS package.[68]We adopted 10×10×4 and 8×8×4k-point mesh for charge selfconsistent calculation, 20×20×8 and 16×16×8k-point mesh for electron—phonon coupling (EPC) linewidth integration, and 5×5×2 and 4×4×2q-point mesh for dynamical matrices ofP4/nmm-II andP4/mmmstructures,respectively.

3. High pressure structures

The most stable phase of all compounds in the ZrXYfamily at 0 GPa isP4/nmm, as shown in Fig. 1(a). TheP4/nmmphase of the ZrXYfamily shows a tetragonal structure formed by the stacking ofX—Zr—Y—Y—Zr layers.[69]

We then performed crystal structure searches for the ZrXYfamily at 50 GP,100 GP,150 GP,and 200 GP,and several new structures were found. The enthalpy difference of given structures is compared with theP4/nmmphase(ground state at 0 GPa). Combining the search results and enthalpy calculations,we successfully identified four new structures at given pressures. As shown in Fig.1,they are theCmcm(space group No. 63) structure, the so-calledP4/nmm-II structure(space group No. 129), theImm2structure (space group No. 44), and theP4/mmmstructure (space group No. 123).The enthalpy—pressure curves of ZrSiSe, ZrGeS,ZrSiSe, and ZrGeSe are shown in Fig. 2. We found that the enthalpy—pressure curves of ZrSiTe, ZrGeTe and ZrSnTe are similar to those of ZrSiSe. The enthalpy—pressure curves of ZrSiTe,Zr-GeTe,and ZrSnTe are attached in Fig.S1.

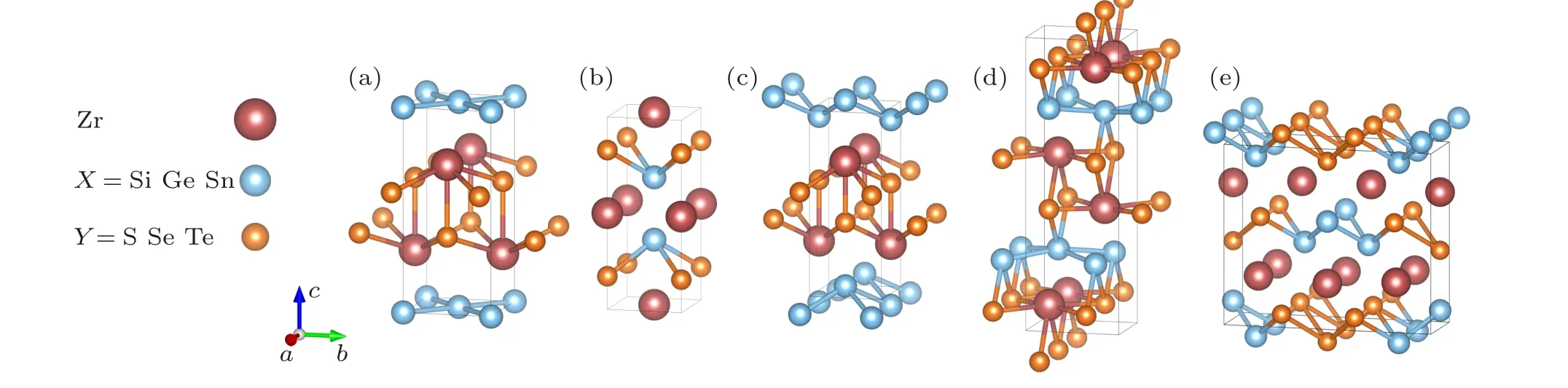
Fig.1. Crystal structures of the high-pressure phases of the ZrXY family: (a)P4/nmm structure,(b)P4/mmm structure,(c)P4/nmm-II structure,(d)Cmcm structure,(e)Imm2 structure.

It is found that (i) ZrX(X= Si, Ge)Se and ZrX(X=Si, Ge, Sn)Te have an identical final high-pressure phase, theP4/mmmphase. The critical pressures of these family members are 102 GPa, 110 GPa, 68 GPa, 62 GPa, and 31 GPa.Because the Zr atom has a relatively large atomic radius,theseXandYatoms tend to be distributed in the Zr layers once pressure is applied. Thus, theP4/mmmstructure is formed with such a type of arrangement:Xatoms andYatoms form a corrugated shape interspersed between two layers of Zr atoms. (ii) The ZrGeSe compound undergoes a series of structural phase transitions:P4/nmm →Imm2→P4/mmm.ThisP4/nmm →Imm2 phase transition occurred at 87 GPa.Remarkably, theImm2 phase has layers formed by puckered triangular chains ofXandYalternating with layers of square nets of Zr. Due to the difference in radius between the Ge and Se atoms, Zr atoms between Ge and Se slightly fluctuate along the Zr plane, which leads to a slightly sparse stack of atoms. (iii) ZrSiS and ZrGeS have an identical final highpressure phase,theCmcmphase. The transition pressures are 100 GPa and 123 GPa. Similar to theP4/nmmphase, thisCmcmphase has two Zr—Ylayers sandwiched between two layers of Si atoms, but its Zr—Ylayers have translated half a lattice along thea-direction accompanied by shortening of the bond length of the Zr atoms along theb-direction. (iv) As shown in Fig.2,ZrGeS undergoes a series of structural phase transitions:P4/nmm →P4/nmm-II→Cmcm. The transition pressures ofP4/nmm →P4/nmm-II are～82 GPa. The highpressureP4/nmm-II phase of ZrGeS shows a very similar pattern to the ambient phase,as shown in Fig.1.Both of them areP4/nmmsymmetry, but the Wyckoff position of the Ge atom is different, from 2csites to 2asites. With the application of pressure,the Ge atoms tend to slide from the middle of the Zr—S square to the vertex of the square. Thus,the Ge layer of theP4/nmm-II structure shifts one-half of the lattice along theaorbaxis, and the two Ge atoms finally form a zig-zag distorted layer. We thus call this new structureP4/nmm-II.For ZrGeS,theaandcaxes of the ambientP4/nmmstructure are 3.25 °A and 7.15 °A,respectively,while theaandcaxes of theP4/nmm-II structure are 3.07 °A and 7.78 °A, respectively. An isosymmetric phase transition is one such phase transition in which the two phases associated with the isosymmetric phase transition possess the same space group but with different Wyckoff sites. This kind of phase transition is always found in some amorphous systems (e.g., liquid—gas transition) or electronic transitions(metal—insulator, valence transitions).[70—72]All of these results prove that theP4/nmmtoP4/nmm-II phase transition is an example of an isosymmetric phase transition. The calculated lattice parameters of these new phases at a given pressure are listed in Table S1.

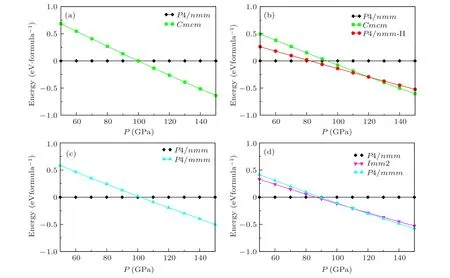
Fig.2. Calculated enthalpy—pressure relationship with respect to ground state. The enthalpy difference of(a)ZrSiS,(b)ZrGeS,(c)ZrSiSe,and(d)ZrGeSe.

4. Stability and mechanical properties

To determine the dynamic stability of these high-pressure phases of ZrXY, the phonon dispersion along the highsymmetry lines was calculated,as shown in Fig.S2.

For allP4/mmmphases, the high-pressure phases show no imaginary frequency modes, indicating that all of these phases are dynamically stable at high pressure. Among thoseP4/mmmphases, ZrGeSe and ZrSnTe have no imaginary frequency modes down to zero pressure; therefore, they might be quenched recoverable under ambient conditions. For theImm2phase of ZrGeSe,phonon dispersion after transition also shows that this is a mechanically stable phase. TheCmcmphases of ZrSiS and ZrGeS show no imaginary frequency modes at high pressure. For ZrGeS,theP4/nmm-II phase has no imaginary frequency at either high pressure or 0 GPa,indicating that this new phase is stable and may be quenchable to recover at 0 GPa.

As the symmetry remains unchanged during the isosymmetric phase transition, we want to compare the mechanical properties of ZrGeS before and after phase transformation.Through crystal symmetry analysis, we have six independent elastic constants, namely,C11,C12,C13,C33,C44, andC66as for these two tetragonal phases.[73]Within the Voigt—Reuss—Hill (VRH) approximation,[63]the macroscopic bulk moduli(B) and shear moduli (G) of a polycrystalline material can be estimated using the elastic constants of the single crystal mentioned in the preceding paragraph. Furthermore,Young’s modulus(Y)and Poisson’s ratio(ν)of the polycrystalline material can be written in terms ofBandGas are well above the limit of the elastic stability,i.e.,C11＞|C12|,2C32＜C33(C11+C12),andC44＞0. We can see that the hardness of theP4/nmm-II phase is 2.71 GPa at 0 Gpa, 1.64 GPa at 90 GPa,which is smaller than that of theP4/nmmphase. To understand the inner principle of this intriguing phenomenon,we calculated the ELF of ZrGeS at 90 GPa with theP4/nmmphase andP4/nmm-II phase.In Fig.3,we show some planes of ELF of the given unit cell while concealing some unnecessary atoms for simplicity and intuition. From the ELF,we can see that the electrons are well localized around the Zr and S atoms,showing good metallicity. However, the electron distribution in the Ge layer changes.In theP4/nmmandP4/nmm-II phases,the electrons between Ge atoms formed covalent bonds. Compared with theP4/nmmphase,the electron distribution density of theP4/nmm-II phase decreases with the prolongation of the bonds,resulting in the weakening of the bond strength. Additionally,the shortening of the Ge—S distance changes the electron distribution between the Ge and S atoms,leading to more metallic bonding. Combining the two aspects above,the softening of theP4/nmm-II phase along thea-axis after the phase transition is comprehensible with theP4/nmmphase.

Fig.3. ELF of ZrGeS at 90 GPa(a),(b)P4/nmm phase;(c),(d)P4/nmm-II phase.

wherek=G/Bis the ratio of the shear modulus to the bulk modulus.

All calculated elastic constants are presented in Table 1.They are positive and obey the Born criterion of mechanical stability.[63]Table 1 indicates that theCi jvalues of this system

Table 1. Calculated elastic constants (Cij), bulk modulus (BH), shear modulus (GH), and Young’s modulus (Y) in GPa as well as the Debye temperature(ΘD),Poisson’s ratio(ν)of ZrGeS-P4/nmm and ZrGeS-P4/nmm-II at 0 and 90 GPa.

5. Electronic properties

The electronic properties of the newly predicted ZrXYare also investigated by calculating their electronic density of states (DOS) and band structures. The results show that all of these newly founded structures are metallic. We show the electronic band structures and DOS of theP4/nmm-II phase of ZrGeS and theP4/mmmphase of ZrGeSe in Fig.4. The band structures and DOS of the remaining newly discovered phase are attached in Fig. S3. For theP4/nmm-II phase of ZrGeS,the DOS near the Fermi level mainly originates from the 4d orbital of Zr, while the contributions from the 4p orbital of Ge and S are quite small. TheP4/mmmstructures of all compounds exhibit similar band structures at high pressure. Likewise,the DOS near the Fermi level mainly originates from Zr atoms,while the contributions fromXandYatoms are small.The total DOS at the Fermi level is found to increase in both IV A and VI A groups as theXatoms move from Si to Ge andYatoms move from Se to Te. We also calculated the surface states of ZrGeS and ZrGeSe,and the results show strong metallic behavior. We showed the surface states of ZrGeS at 0 and 90 GPa in Fig.S5.

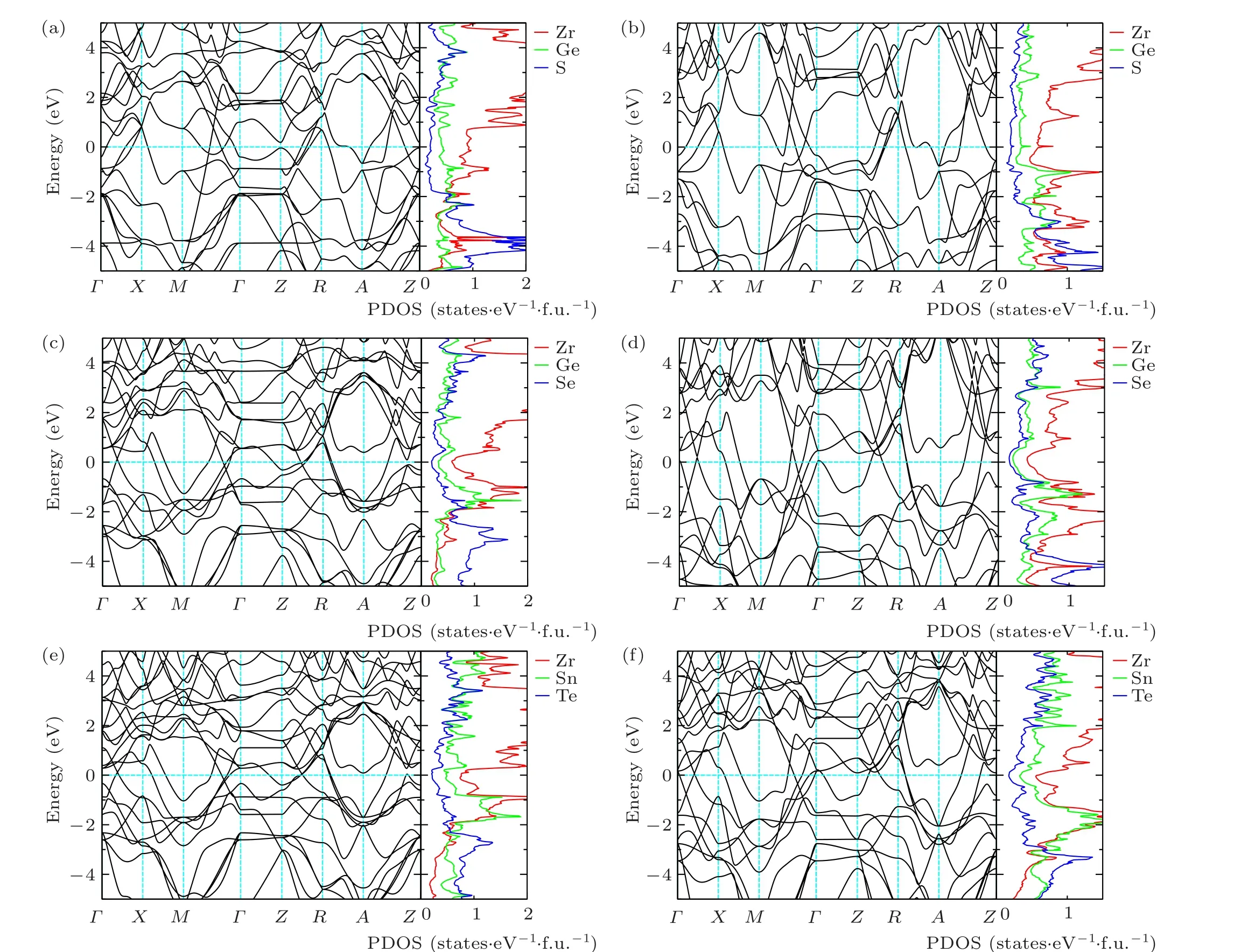
Fig.4. Calculated band structure. (a),(b)Band structures of the P4/nmm-II structure of ZrGeS at 0 GPa and 90 GPa. (c),(d)Band structures of the P4/mmm structure of ZrGeSe at 0 GPa and 120 GPa.

6. Superconductivity

Considering that the metallic high-pressureP4/nmm-II phase of ZrGeS and theP4/mmmphase of ZrGeSe remain stable at 0 GPa, we studied the superconducting properties of ZrGeS and ZrGeSe.

The superconducting critical temperature (Tc) is estimated using the modified Allen—Dynes McMillan equation[74,75]

The electron—phonon coupling constant(λ)can be evaluated using the relation

We showed theα2F(ω) and accumulated EPC strengthλ(ω)of these two structures at 0 GPa and transition pressure,respectively,for comparison. We also plotted the phonon dispersion and linewidth of the phonon spectrum.

Fig.5.Phonon spectra(left),phonon density of states projected onto selected atoms(middle),α2F(ω)and accumulated EPC strength λ(ω)(right).The size of the circles on the phonon dispersion is proportional to the EPC strength.(a)and(b)P4/nmm-II structures of ZrGeS at 0 GPa and 90 GPa.(c)and(d)P4/mmm structures of ZrGeSe at 0 GPa and 120 GPa.

For ZrGeS,the phonon DOS is separated into two regions at both pressures. The low-frequency modes(0—200 cm-1)at 0 GPa and (0—363 cm-1) at 90 GPa are associated with vibrations of heavy Zr and Ge atoms,while the high-frequency branches (220—330 cm-1) at 0 GPa and (380—525 cm-1) at 90 GPa mainly originate from S atoms. The high-frequency part of phonon DOS is slightly different at 0 GPa and 90 GPa.At 90 GPa, the high-frequency part contains a small portion of Zr atom vibrations, which cannot be neglected, while at 0 GPa, almost all high-frequency phonon DOSs arise from S atoms. This is understandable because at high pressure, the shorter in-plane bond of Zr and S gives the relatively larger phonon DOS of Zr. From the phonon dispersion, it can be seen that when the pressure drops,the phonon modes are softened without a significant change in shape. Meanwhile, the EPC strength contributed by the low frequency at 0 GPa is stronger than that at 90 GPa. From Figs. 5(a) and 5(b), we can tell that almost all of the phonon modes contribute toλat 0 GPa and 90 GPa. In contrast,high-frequency phonon modes at 0 GPa contribute approximately 20% to the totalλ, while at 90 GPa, high-frequency phonon modes contribute approximately 34% ofλ. Although high-frequency phonon modes contribute more at high pressure,theirTcdrops as all the spectra harden. Our theoretical analysis provides the estimation of EPCλ=0.75, logarithmic average frequencyωlog=197 K,andTc=8.10 K with a commonly used Coulomb repulsion coefficient ofμ*= 0.1 at 0 GPa. At high pressure, the phonon dispersion hardened,and combined with shrinkage of the phonon dispersion linewidth,Tcdecreased to 1.48 K at 90 GPa withλ=0.395,ωlog=380 K.

For ZrGeSe,our theoretical analysis provides the estimation ofλ=0.75,ωlog=197.6 K,Tc=8.04 K withμ*=0.1 at 0 GPa, while at 90 GPa,λ= 0.337,ωlog= 348.4 K,Tc=0.47 K. For phonon DOS, unlike ZrGeS, all the atoms are involved in the entire frequency range. This is consistent with the expectations of the relatively strong bonding of Zr,Ge, and Se atoms. From Figs. 5(c) and 5(d), we can clearly see that as the pressure drops,both the phonon dispersion and phonon DOS are greatly altered. The phonon DOS of ZrGeSe at 120 GPa in the high-frequency region at approximately 384 cm-1accounts for a relatively large portion of the total phonon DOS.As pressure drops,the phonon DOS of these high-frequency regions has mostly changed,except for two energy regions: one is approximately 220 cm-1of Se and the other is 204 cm-1of Zr and Ge. From the phonon dispersion,it can be seen that some modes of ZrGeSe are significantly softened,especially along theG—X—M—Gpath. The largest e—ph coupling values occur forX(0,0.5,0) andG(0,0,0), and these modes with maximal coupling are depicted in Fig.6. As shown in Fig.6(a),for high symmetry pointX,the vibrations are composed of(I)a relative motion mode of the Zr1 and two Ge atoms along thec-axis and(II)a mode where the two layers of Se atoms move in opposite directions along thea-axis.In Figs. 6(b)—6(d), we display three different modes for high symmetry pointG: Fig. 6(b), Zr1 and Zr2, Ge and Se atoms relatively vibrate along the(1,1/2,0)direction;Fig.6(c),Zr1 and Zr2, Ge and Se atoms relatively vibrate along theb-axis;Fig. 6(d), Zr1, Se and Ge atoms relatively vibrate along thec-axis. These modes shift from～200 cm-1at 90 GPa to～50 cm-1at 0 GPa. We can then distinguish three regions inα2F(ω) at 0 GPa: a low-energy region from 29 cm-1to 79 cm-1,an intermediate region from 79 cm-1to 196 cm-1,and a high-energy region from 196 cm-1to 234 cm-1. We found that the relative contributions of each region are considerably different. The low-energy modes contribute～19.5%of the totalλ, intermediate-energy modes contribute～73%ofλ,and high-energy modes contribute～7.5%ofλ.

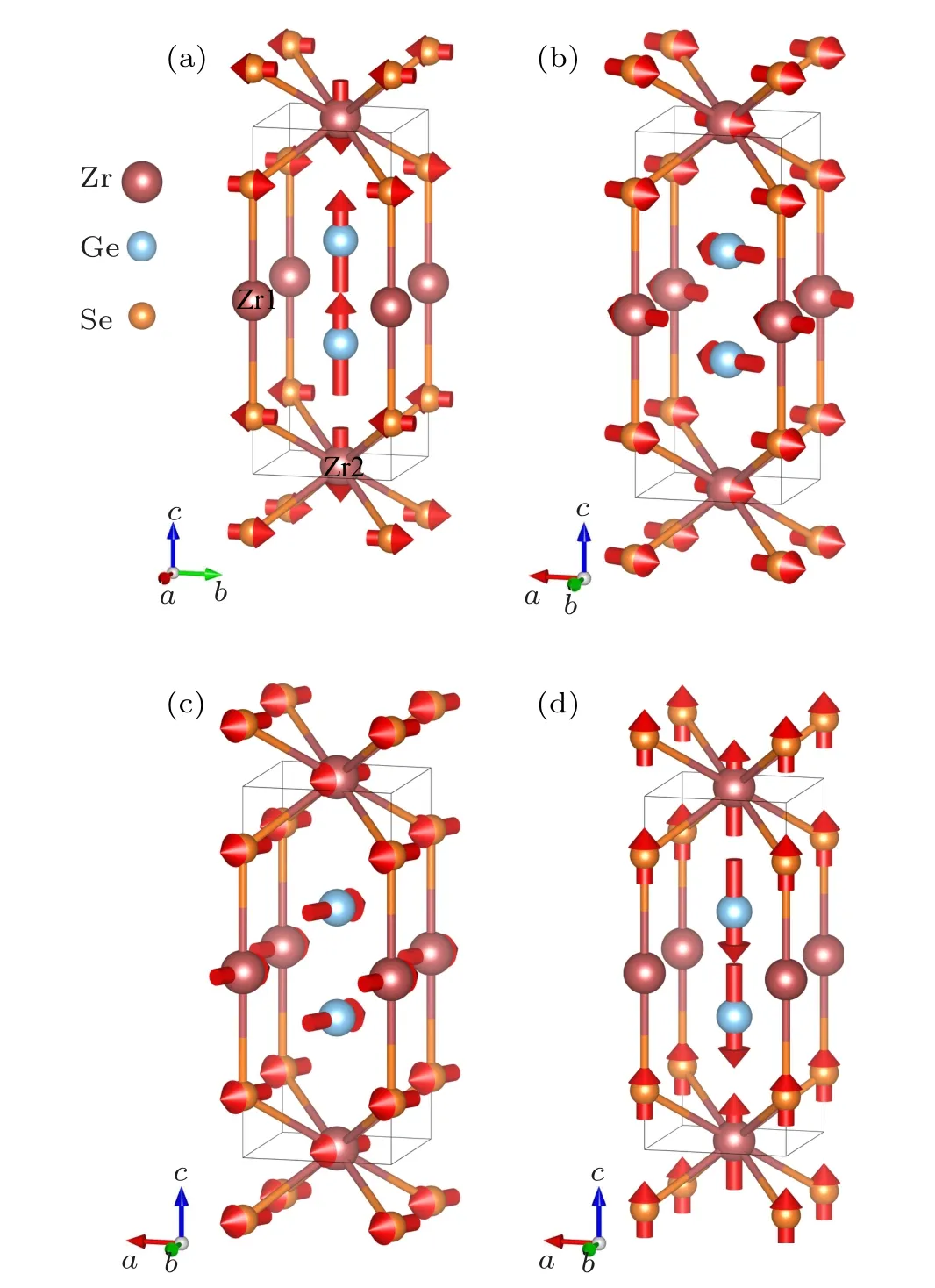
Fig.6. Vibration of the relative motion mode of(a)X and(b—(d)G.

7. Conclusion

We carried out crystal structure predictions of the ZrXYsystem under high pressure. Four new structures were found,namely,P4/nmm-II,Cmcm,Imm2, andP4/mmm. The calculation results of the formation energy, phonon spectra, and mechanical stability indicate that the high-pressure structures are stable. TheP4/nmm-II structure of ZrGeSe and theP4/mmmstructure of ZrGeSe have no imaginary frequencies at 0 GPa, which indicates that they may be quenchable to atmospheric pressure. TheP4/nmmstructure of ZrGeS undergoes an isosymmetric phase transition, and the hardness of the denser structure is less than that of the initial structure,which is somewhat anti-intuitive since the hardness usually increases with density. TheP4/nmm-II phase of ZrGeS and theP4/mmmphase of ZrGeSe are superconductors. TheTcof the two phases gradually increases with decreasing pressure,from 1.5 K at 90 GPa to 8.1 K at 0 GPa and 0.5 K at 90 GPa to 8.0 K at 0 GPa, respectively. Our study expands the understanding of ZrXYsystems under high-pressure conditions and provides theoretical guidance and support for high-pressure superconductivity in this family.

Acknowledgments

J.S. thanks the financial support from the National Natural Science Foundation of China (Grant Nos. 12125404,11974162, and 11834006) and the Fundamental Research Funds for the Central Universities, China. The calculations were carried out using supercomputers at the High Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures,the high-performance supercomputing center of Nanjing University.