Energy levels and transition data of 3p63d8 and 3p53d9 configurations in Fe-like ions(Z=57,60,62,64,65)

Bao-Ling Shi(施宝玲) Yi Qin(秦毅) Xiang-Fu Li(李向富) Bang-Lin Deng(邓邦林)Gang Jiang(蒋刚) and Xi-Long Dou(豆喜龙)

1Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China

2College of Electrical Engineering,Longdong University,Qingyang 745000,China

3College of Geophysics,Chengdu University of Technology,Chengdu 610059,China

Keywords: Fe-like ions,energy levels,wavelengths,transition rates

1. Introducti on

Atomic structure parameters have been considered as a promising approach to improve our understanding of the physical processes of astrophysical plasmas.[1—4]On the other hand,knowledge of emission lines generated by these high-Zelements is essential for the abundance of stars.[5]It is therefore a continuous focus of attention. Considerable attempts,including laser-produced plasmas, grazing-incidence spectrographs,electron-beam ion trap(EBIT),tokamak plasmas,etc.,have been devoted to excavating these atomic data and won considerable achievements.[6—11]However,the current atomic data are still insufficient in explanation of the existing results.

Among these highly charged ions, of particular interest are Fe-like ions. Its wavelengths and transition rates are useful for studying the abundance of stars.[12,13]Experimentally the spectrum of Fe-like ions is primarily produced by laserproduced plasmas. Its emission lines, in general, range from x-ray to extreme ultraviolet(EUV)spectral regions.[14]These emission spectrums have profound implications not only for spectral diagnosis in inertial confinement fusion experiments,but also for analyzing the abundance of galaxy clusters and the geometry of star flares.[15]These applications stimulated extensive researches on atomic structure parameters for Felike ions. Ekberget al.[16,17]investigated the landscape of energy levels and wavelengths of the 3p63d8—3p53d9E1 transitions configurations for Fe-like ions(44≤Z ≤70)using laserproduced plasmas and grazing-incidence spectrographs. The measured wavelengths are significant for the determination of quantum electrodynamics effects in highly charged ions.Ralchenkoet al.[18]and Radtkeet al.[19]identified E1 and magnetic dipole (M1) emission lines of Fe-like W ion using the Berlin EBIT. Their results indicated that some of the M1 lines are extremely useful towards the diagnosis of temperature and density of hot fusion devices. Louzonet al.[20]proposed the x-ray spectrum,in wavelengths ranging from 8 °A to 10 °A, and identified resonance transitions 3d—4f, 3d—5f, 3p—4d, and 3d—4p of Fe-like Sm ion employing laser-produced plasmas. Such measured wavelengths play a major role in testing the most advanced theories of relativistic atomic structure. The L-shell emission lines from Fe-like Au53+ion are reported by Brownet al.[21]Its strong 3d5/2→2p3/2emission lines can be used for diagnosing charge state distribution in high energy density plasmas, for instance, those identified in the laser inlet hole of a hot cavity radiation source.With the aid of these experimental data, theoretical calculations not only enrich the family of HCIs,but also provide key insights into the identification of measured lines and explanation of the existing results. Guoet al.[5]predicted the energy levels, transition probabilities, and wavelengths of 3d8ground configurations in Fe-like Hf,Ta,W,and Au ions using the second-order relativistic many-body perturbation theory(RMBPT)and the parallel RCI methods. Taking advantage of the reliable Flexible Atomic Code(FAC)and MCDHF as well as multi-configuration Dirac—Fock(MCDF)methods,the theoretical group has filled a gap in excitation energies,oscillator strengths,wavelengths,line strengths,radiative lifetimes,transition rates of electric quadrupole(E2),and M1 transitions of the 3s23p63d8ground configurations for Fe-like ions(Z=72—83).[22—24]

Despite intensive experimental and theoretical efforts,there is still a lack of complete and unambiguous atomic data of lanthanide elements. The atomic data of lanthanide elements were expected in many high-tech fields, including lighting, optoelectronic applications, atomic clocks, and so on.[25]These absent lines of lanthanide elements in different ionization stages contribute crucially to detecting the growth of peculiar stars in astrophysics.[26]Moreover, lanthanides were used for studying the ejected materials of neutron star mergers, especially for addressing nucleosynthesis and star formation.[27]Of particular interest are some emission lines of La and Sm ions found in the spectra of solar flares and corona.[28]In addition,it should be stressed that integrated radiation data of highly charged Gd and Tb elements are needed for the next generation of EUV lithography as the origin of light sources.[29]Unfortunately, little has been decided about the available atomic data of lanthanide elements,in particular Fe-like ions(Z=57,60,62,64,65),needed for laboratory and astrophysical plasmas modeling and diagnosing.

In this paper,we established a consistent set of energy levels,wavelengths,transition rates,oscillator strengths,and line strengths for the lowest 21 states of 3p63d8—3p53d9E1 transitions configurations in Fe-like ions (Z=57,60,62,64,65)using the MCDHF method. The correlation effects of VV and CV electrons were systematically considered. Meanwhile,we employed Breit interaction and QED corrections to treat accurately atomic state wave functions. Our results are in excellent agreement with the previous observations, indicating that our theoretical calculations are reliable. Moreover, we predicted some new transition data, offering actionable insights for future experiments. The layout of this paper is as follows: In Section 2, we introduce the theoretical methods and calculational details. In Section 3,we present the results and discussions of our calculated atomic parameters. We make a summary in Section 4.

2. Methods

2.1. MCDHF theory

In this paper, all of our calculations are carried out on basis of the MCDHF[30—32]approach, as implemented in GRASP2018 general relativistic atomic structure code.Some significant details have been extensively discussed elsewhere,[33—38]in which the Dirac—Coulomb Hamiltonian can be expressed as

wherePis the parity,JandMbeing, respectively, the total angular quantum number and the magnetic quantum number.NCSFsis the number of CSFs andcidenotes the configuration mixing coefficients for the statei.γirepresents other appropriate labeling of the configuration state functioni, e.g.,coupling scheme and orbital occupancy. The calculations on many levels are performed in the so-called extended optimal level (EOL) scheme. Under the relativistic self-consistent field (RSCF) procedure,[39]both the radial parts of the Dirac orbitals and expansion coefficientsciare optimized to selfconsistency.[39]In calculations based on the subsequent RCI,the Breit interaction

where Δx=Ex(experiment)/Ex(theory),x=fs presents the fine structure of a given spectral term.

2.2. Transition parameters

whereAlandAvare transition rates in length and velocity forms,respectively.

2.3. Calculational procedure

For Fe-like ions, in our calculations, 1s22s22p63s2is treated as the core electrons. The even and odd parities belonging to 3p63d8and 3p53d9configurations were calculated separately. CSFs are obtained by the active set approach,[49]by allowing single and double(SD)excitations from then=3 shells of reference configurations to active set of orbitals withn ≤7,l ≤4, in which only one electron substitutions are allowed from the 3s core-shell. No substitutions are allowed from then=1,2 shells,which is defined as an inactive closed core. VV and CV electron correlation effects are generally considered in this way. Taking into account the lists of CSFs increase very rapidly with the expanding active set of orbitals,we only retain the CSFs that directly interact with it in the reference configurations.[22—40]To check the convergence of computed parameters,active orbitals are enlarged step by step in a systematic way. The optimization is also layer by layer.At each stage, the newly added orbitals are optimized, while the previous ones are fixed. After that, Breit interaction in the low-frequency limit and QED corrections(e.g.,self-energy and vacuum polarization)are included in the RCI calculations.

3. Results and discussion

3.1. Energy levels

We begin by monitoring the convergence of our MCDHF calculations. For Fe-like Sm36+ion,the resulting energies of the lowest 21 states belonging to the 3p63d8and 3p53d9configurations with respect to increasing active set of orbitals are concluded in Table 1. Obviously, from Table 1 we can find the energy differences between adjacentnare decreased gradually upon increasing active set of orbitalsn. For these energy levels, the mean relative differences are around 0.36%,0.22%, 0.01%, and 0.01% for calculations based on the expansion fromn=3 and expansions obtained from SD excitations to active setsn=4, 5, 6, and 7. The calculated energy levels of all states atn=7 active orbital are almost the same as those of all states atn=6 active orbital. The maximum difference betweenn=7 andn=6 calculations is even less than 132 cm-1.Such facts indicate the energy levels have converged when the active set of orbitalsnis increased to 7. Subsequently, the same computational scheme then proceeded to monitor the convergence of other Fe-like ions(Z=57,60,64,65). Similar to Fe-like Sm36+ion,we concluded that these selected ions possess identical trends of variation in energy upon increasing active set of orbitals. Excitation energies were predicted to converge successfully with active set of orbitalsnincreased to 7. Atn=7,the identified maximum differences are 152 cm-1,138 cm-1,127 cm-1,and 77 cm-1for Fe-like ions(Z=57,60,64,65)relative ton=6 calculations,respectively.The computed energy levels withn=7 are presented in Table S1 of supporting information for all Fe-like ions(Z=57,60,62,64,65).

For comparison, the experimental values by Ekberget al.[16]using laser-produced plasmas and the energy differences between theoretical and experimental results are summarized together in Table S1 of supporting information. From the inspection of Table S1, it should be pointed out that our simulated energy levels, aside from four levels (3p63d83P0,3p53d93P0, 3p53d93F2, and 3p53d91P1), agree fairly well with experimental results for Fe-like Sm36+ion,with the difference less than 1000 cm-1. The energy level of 3p53d93F2state is determined to be 3769876 cm-1,which deviates from experimental value(3771340 cm-1)up to 1464 cm-1,the reason behind this is that the CV correlation effect arising from subshell 2p is not included in our calculation. Prior literature has found that these facts have a significant impact on energy levels.[50,51]Herein, since the limitation of available computational resources, the electron correlation effects are not fully considered. In fact, the atomic parameters of Felike Sm36+ion have been investigated by Ivanovaet al.[52]by means of the relativistic perturbation theory method of the zero-approximation model.For reference,their computed data together with energy differences compared to available data reported by Ekberget al.[16]are summarized in Table S1 of supporting information. It is apparent that most of the energy levels deviate from the experimental values significantly.For example, we note that the energy levels of 3p63d83P0,3p53d93P0,3p53d93P2,3p53d91F3,and 3p53d93F2states are reported to be 162800 cm-1,2829200 cm-1,3634600 cm-1,3695800 cm-1, 3763600 cm-1, respectively. These results are far away from experimental values up to 6210 cm-1,6290 cm-1, 7630 cm-1, 8790 cm-1, and 7740 cm-1. Compared with the relativistic perturbation theory method of the zero-approximation model, we concluded that MCDHF calculations with the inclusion of electron correlation effects and higher-order corrections are more suitable to investigate atomic parameters of Fe-like ions. Subsequently,we proceed to investigate energy levels of other Fe-like ions(Z=57, 60,64,65)using MCDHF method,the obtained results are listed in Table S1 of supporting information. Meanwhile,in the last column of Table S1,we list the estimated uncertaintyδEfsbetween the present energy levels and experiment values. Our results for energy levels of these Fe-like ions are in good agreement with observed ones by Ekberget al.[16]The relative deviations are within 0.1%except for a few states,of which the largest relative difference is about 0.8% for the 3p63d83P0state. We expect that the current results can be used as a reference for other calculations of Fe-like sequence ions.

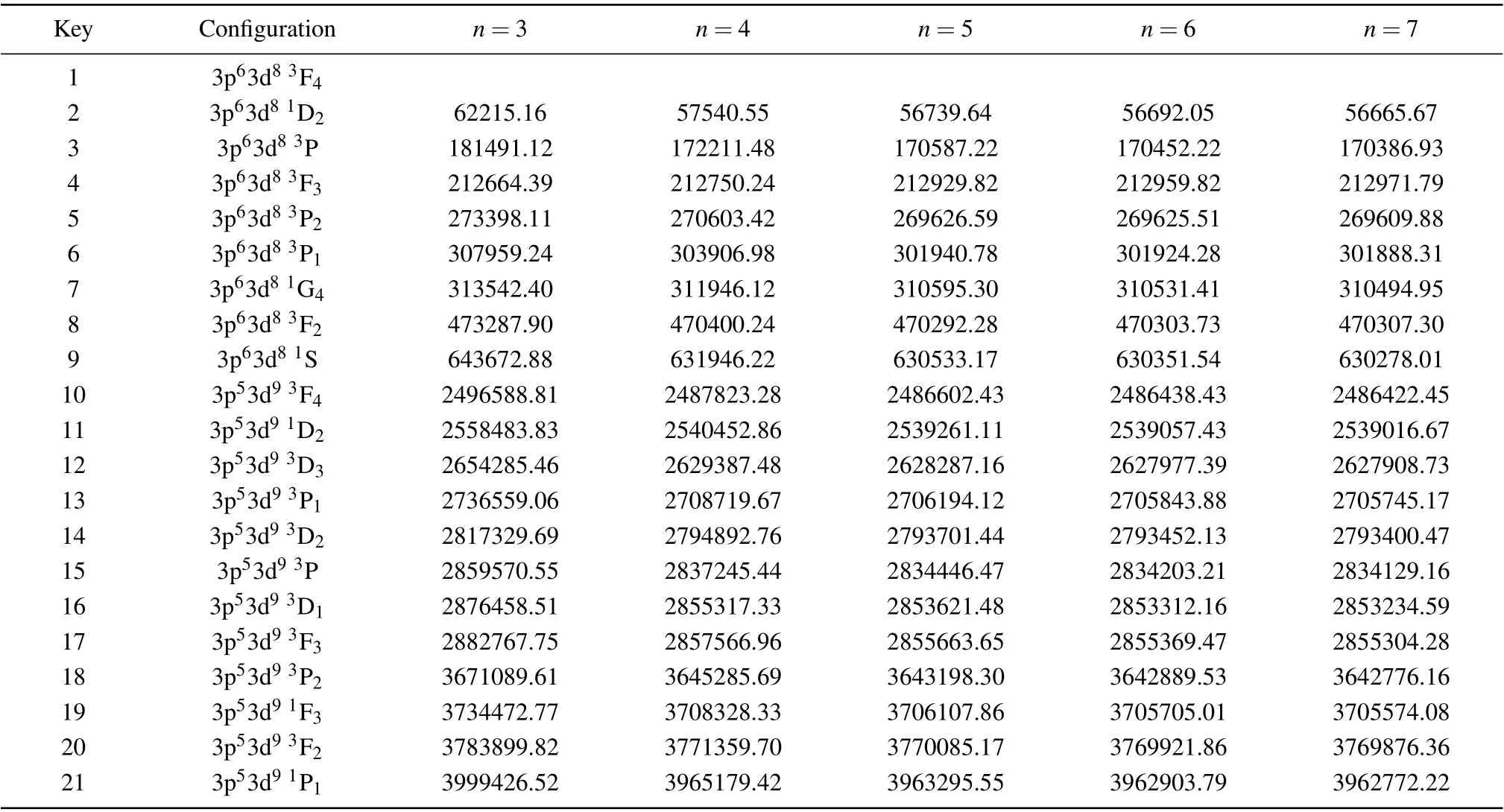
Table 1. Energy levels(all in unit cm-1)for the lowest 21 states in Fe-like Sm36+ ion as a function of increasing active sets of orbitals.

Figure 1 shows the contribution of Breit interaction and QED corrections to the excitation energies for the lowest 21 states of 3p63d8and 3p53d9configurations in Fe-like Sm36+ion. As displayed in Fig. 1, the total (Breit and QED) corrections reduce excitation energies by about 0.16%—2.09%and narrow the gap between the theoretical values and experimental observations, especially for the 3p53d93F2state,in which the energy is significantly decreased by around 30000 cm-1. By contrast, the 3p63d81D2and 3p63d83P0states have somewhat higher energies than Coulomb energies by about 3000 cm-1and 5000 cm-1, respectively. And the accuracy of energies improved by about 5.48% and 3.20%.Overall, the improved agreement between the theoretical and experimental results suggests it is highly necessary to incorporate Breit and QED corrections for RCI calculations of the highly charged heavy ions.[53]Subsequently, we identify respectively the influence of Breit interaction and QED corrections on energy levels. The Breit correction reduce all energy levels (relative to Coulomb energies) of the 3p63d8and 3p53d9configurations by about 0.29%—2.21% (Fig. 1), with two exceptions: 3p63d81D2and 3p63d83P0, respectively,in which the energies are higher than Coulomb energies by around 5.50% and 3.19% (Fig. 1). It should be stressed that the QED corrections have little effect on energy levels, the contribution to the energy levels appears in the range of around 0.01%—0.18%. We,therefore,concluded that Breit interaction is the dominant contribution to energy in the higher-order corrections.

Figures 2 and 3 present the effects of Breit interaction and QED corrections on energy levels of 3p63d8and 3p53d9configurations along the sequence, respectively. In Fig. 2, note that there are identical variation tendencies for levels 4 and 5,levels 7 and 9, levels 10 to 13, levels 14 to 17, thus we only present levels 2 to 4,levels 6 to 8,level 10,level 14,levels 18 to 21. It is shown from Fig. 2 that the contribution of Breit interaction is improved for each level considered with the nuclear charge Z increasing. The reason behind this is that the attraction between the nucleus and the extranuclear electrons is positively correlated with the nuclear chargeZ. It is well known that Breit interaction is the embodiment of the interaction between electrons,[54]the Breit interaction thus enhance accordingly. Figure 3 shows the effect of the QED corrections on energy levels with respect to Z. Similarly, we only show levels 2 to 4,level 8,level 10,level 14,levels 18 and 20.Notably,these levels have the consistent tends for levels 4—7,levels 8 and 9, levels 10—13, levels 14—17, levels 18 and 19,levels 20 and 21,thus the latter is ruled out here. From Fig.3 we found that the contribution of QED effects, as expected,increase with the increase ofZfor a majority of the levels,this is because the QED corrections are proportional toZ4. While for levels 3 and 20, the increasingZleads to a reduction of the QED contribution,which is consistent with the conclusion summarized by Malyshevet al.[55]and Huet al.[56]

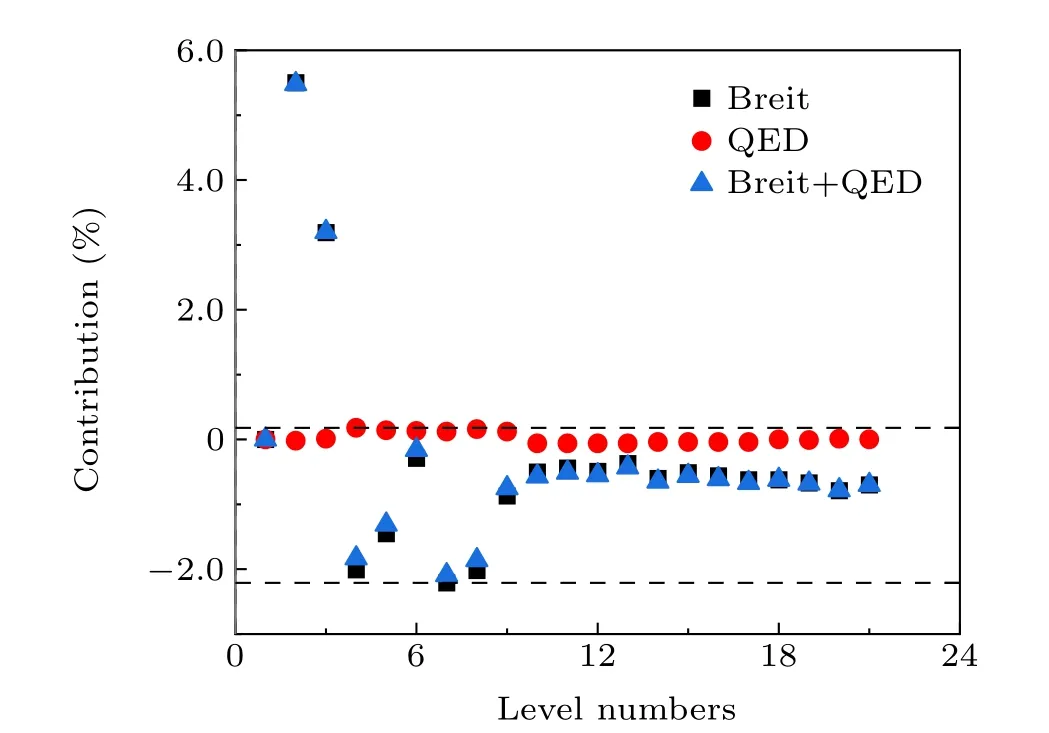
Fig.1. Corrections of Breit and QED effects to the MCDHF energies for the lowest 21 states of 3p63d8 and 3p53d9 configurations in Fe-like Sm36+ ion,all energies are relative to the ground state.

Fig.2. Contribution from Breit interaction to the energy levels of 3p63d8 and 3p53d9 configurations for Fe-like ion as a function of nuclear charge Z.

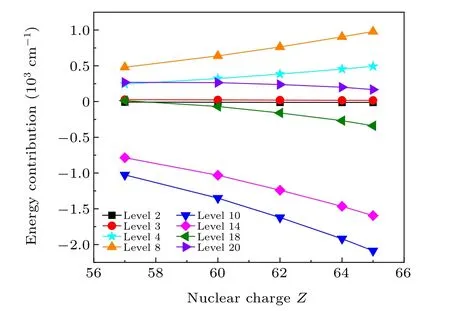
Fig. 3. Contribution from QED corrections to the energy levels of 3p63d8 and 3p53d9 configurations for Fe-like ion as a function of nuclear charge Z.

3.2. Transition parameters

Having decided the energy levels of all Fe-like ions(Z=57, 60, 62, 64, 65), we further investigated the wavelengthsλ, transition ratesA, weighted oscillator strengthsg f, line strengthsS,and uncertainty estimators dTof 3p63d8—3p53d9E1 transitions configurations using MCDHF method. The resulting data are listed in Tables S2—S6 of supporting information. The E1 transition rates are given in both velocity (v)and length (l) forms. Our MCDHF transition rates in velocity forms(Av)and length forms(Al)show good agreement for strong transitions. Such results can be used as an indicator to verify the reliability of our calculations.[57]It should be noted that, however, there are substantial discrepancies betweenAvandAlfor some weak transitions, this may be attributed to a small imbalance arising from correlation effects that alter the transition rates significantly in one of the gauges.[58]The other transition parameters, including weighted oscillator strengthsg fand line strengthsS, are presented with the length form,there is a widespread consensus which is generally thought to be more accurate than the velocity form.[59,60]

In Table 2, we have compared the E1 transitions wavelengths of Fe-like La31+,Nd34+,Sm36+,and Gd38+ions with the available experimental values. Interestingly, it is apparent from Table 2 that our E1 transitions wavelengths are overall consistent with the available experimental values reported by Ekberget al.[16]again validating our calculation scheme.As shown in Table 2, for Fe-like Sm36+ion, in most cases,our MCDHF wavelengths are shorter than the observations.Comparing our calculated and experimental values, the striking difference has been predicted to occur in the 3p63d81G4→3p53d91F3transition level,whose value is-0.017 °A(relative difference of 0.058%), which is quite satisfactory. Regarding Fe-like La31+, Nd34+, and Gd38+ions, the greatest deviation between our MCDHF values and experimental ones is found to be 0.041 °A,and the relative deviation of about 0.13%.Thus, we can conclude with confidence that our computed wavelengths are highly accurate,which is enough to determine ground state correlation effects and quantum electrodynamics effects in highly charged ions.

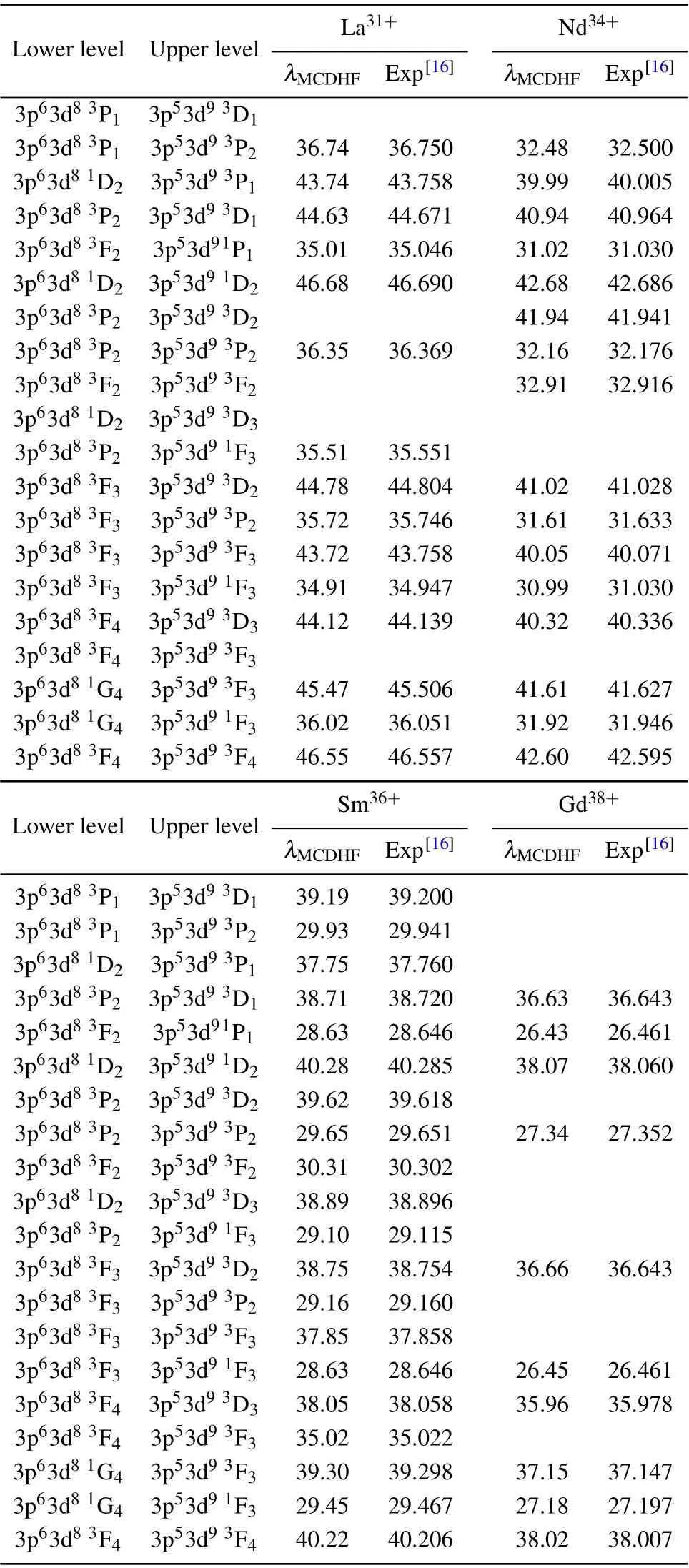
Table 2. Comparison of wavelengths(in unit °A)for E1 transitions with the experimental values in Fe-like La31+,Nd34+,Sm36+,and Gd38+ ions.

Finally,we estimate uncertainty dTon the transition rateA(in unit s-1) for Fe-like Sm36+ion. It is widely accepted for evaluating the quality of E1 transition rates. The smaller the uncertainty dT, the higher quality of E1 transition rates.As shown in Fig. 4, the uncertainty dTagrees within 10%for most of the strong transitions. Moreover, for the strong lines observed from 3p63d83P1→3p53d93D1together with 3p63d83P2→3p53d93D2transitions, the uncertainty dTis well below 0.1%. In contrast to these stronger transitions,the uncertainty dTis relatively larger for the small amounts of weaker transitions. This situation is reasonable and has a precedent, where the authors found that some weaker transitions are composed of two-electron or intercombination lines transitions, the transition rates for this kind of transition are difficult to compute accurately.[61,62]

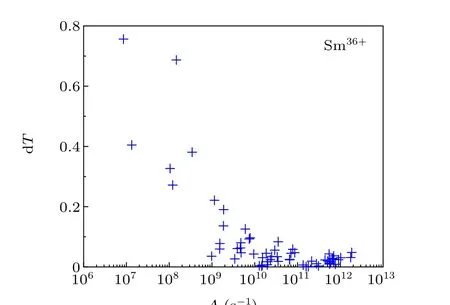
Fig.4. The uncertainty estimators dT for transition rates A(in unit s-1)of E1 transitions in Fe-like Sm36+ ion.

4. Conclusions

Using the MCDHF method, we have performed a comprehensive investigation on the energy levels among the lowest 21 states of the 3p63d8and 3p53d9configurations in Fe-like ions(Z=57,60,62,64,65). Our results of energy levels are in good agreement with available experimental measurements.The relative differences agree with within 0.1%for a majority of the energy levels. Our detailed discussion suggests that it is highly necessary to consider electron correlation effects and higher-order corrections in calculations of the highly charged heavy ions. For transition data, we have reported the transition wavelengths. Compared with the experimental data, the overall deviation is well below 0.041 °A.The uncertainty dTof transition rateA(in unit s-1)agree to within 10%for most of the strong E1 transitions. Overall, our calculations indicated that the MCDHF method with the inclusion of more electron correlation effects and higher-order corrections is more accurate than the relativistic perturbation theory approach towards identifying atomic data of Fe-like ions. Additionally,we have obtained a new set of transition parameters, namely, wavelengths,transition rates,weighted oscillator strengths,and line strengths for E1 transitions. These results would benefit lines identification, modeling of astrophysical and laboratory plasmas.

Acknowledgment

The authors express sincere appreciation to professor J¨onsson P for providing the GRASP2018 program for free.