Maximum entropy mobility spectrum analysis for the type-I Weyl semimetal TaAs

Wen-Chong Li(李文充) Ling-Xiao Zhao(赵凌霄) Hai-Jun Zhao(赵海军)Gen-Fu Chen(陈根富) and Zhi-Xiang Shi(施智祥)

1School of Physics and Key Laboratory of MEMS of the Ministry of Education,Southeast University,Nanjing 211189,China

2Beijing National Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

Keywords: Weyl semimetal,mobility spectrum analysis,magnetoresistance,electrical transportation

1. Introduction

Studying new quantum materials such as topological insulators, Dirac materials and Weyl semimetals (WSMs) is of great importance in condensed matter physics because of their abundant physical properties and application potentials.[1–5]For WSMs,according to whether the Weyl cone is tilted,they can be divided into two categories: type-I and type-II.Recent first-principles calculations predicted a family of nonmagnetic WSM including TaAs,TaP,NbAs,and NbP.[6–11]Large magnetoresistance(MR)and low field Shubnikov–de Haas(SdH)oscillation were predicted.[8]These unique electronic structures and peculiar physical properties suggest that the WSM shows interesting physics and has potential future applications.

First-principles calculation predicted that TaAs is a type-I WSM with data-like W1 pockets and dot-like W2 pockets.[7]Ultrahigh mobility (μe≈18 m2·V-1·s-1at 10 K) and extremely large positive MR (80000% at 1.8 K in a field of 9 T)were discovered.[7]Surprisingly,negative MR is observed when the magnetic field is parallel to the current. Moreover,unlike ordinary metals or semiconductors,the SdH oscillations can be observed at a very low field. Detailed analysis indicates that there are two types of carrier in TaAs,in agreement with first-principles calculations.[6–8]However, how to quantitatively analyze the conducting behaviors of different types of fermions and how to study their evolution with temperature and magnetic field are still open questions,which may give answers to many interesting experimental observations including unsaturated MR and low field SdH oscillation.

Mobility spectrum analysis (MSA)[12–16]is a useful tool for extracting carrier information from experimentally measured longitudinal and transverse electric transport curves. It has previously been used for Ba(FeAs)2and FeSe superconductors[17,18]and type-II Weyl semimetals Td-MoTe2.[19]Recently, maximum entropy mobility spectrum analysis(MEMSA)has been used forβ-PtBi2.[20]Compared with other methods, MEMSA has higher resolution, and can perfectly fit the MR and Hall resistance data. In this paper,we use MEMSA to analyze the experimentally measured MR and Hall resistance of TaAs, from which mobility spectrum(MS)is obtained. MSA successfully distinguishes between the conductivity contributions of two different Weyl fermions (W1 and W2) at all experimentally measured temperatures. Our results give important clues for understanding the large and non-saturating MR in a TaAs single crystal.

2. Method

Within MS theory, the conductivity tensor is given by[14–18,20]

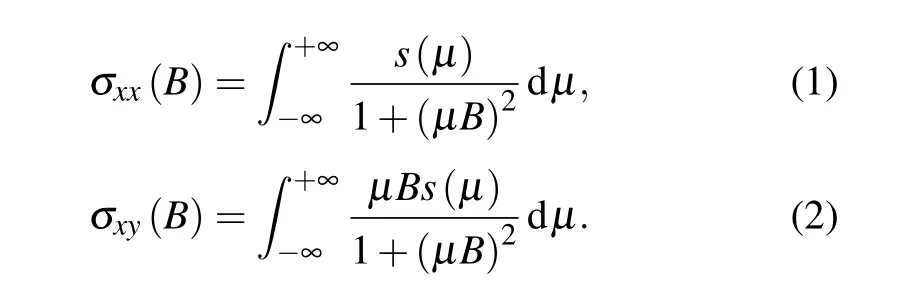
Here,s(μ)=eμdn/duis the mobility spectrum,n(μ)is the density for carriers with mobilityμ. Equations(1)and(2)can be solved numerically using MEMSA. Details of the method can be found in Refs.[15,20].

3. Results and discussion

3.1. Mobility spectrum of TaAs

The MS of TaAs for temperaturesT=1.8 K,10 K,40 K,80 K, 100 K, and 120 K are shown in Figs. 1(a)–1(f), respectively. The corresponding fitting curves to experimentally measured magnetic conductivityσxx(B)/σxx(0)and Hall conductivityσxy(B)/σxx(0) are shown in Figs. 2(a) and 2(b). It is clear that MS nicely fits the experimental data, benefitting from the MEMSA method.

We now compare our MS results with reported firstprinciples calculations. According to Ref.[7],the band structure of TaAs contains a data-like Weyl pocket (W1) 21 meV below the Fermi surface, and a dot-like Weyl pocket (W2)about 2 meV above the Fermi surface. Therefore, the dominant carrier is the electron for W1, and is the hole for W2.At low temperatures (T ＜40 K), our MS also contains two dominant pockets: one electron pocket and one hole pocket(see Figs. 1(a)–1(c)). Therefore, we mark the big electron peak witheW1,and the big hole peak withhW2. Holes for W1 and electrons for W2,in principle,can be thermally activated.There are two small peaks on our MS at low temperatureT,which grow big after increasingT. Therefore,they very likely originate from W1 and W2(we mark them withhW1andeW2,respectively). Other carriers coming from ordinary pockets should have mobilities that are smaller than that of the best normal metal conductors(e.g.,μ ≈0.6 m2·V-1·s-1for silver at 5 K[21]). No such peak with small mobilities is observed in our MS curves,indicating that conductivity contributions from ordinary pockets are too small to be detected by transport measurement.

The MS is sensitive to temperature. In general, with increasing temperatureT, the number of peaks remains unchanged forT ＞120 K (see Figs. 1(a)–1(f)). However, peak positions(corresponding to mobilities)as well as heights(corresponding to charge densities),greatly vary with temperature.For peak positions, as shown in Figs. 1(a)–1(f), almost all peaks move toward the low mobility direction(i.e.,mobilities decrease)as temperature increases. However, the mobility ofeW1decreases faster than that ofhW2.

As a result,gradually,the mobility ofhW2approaches that ofeW1,and the MS becomes symmetric. For peak heights,the peaks ofeW1andhW2decrease with increasing temperature,whereas those ofeW2andhW1increase. At high temperatures(T ＞40 K),the height of all four peaks is equal.

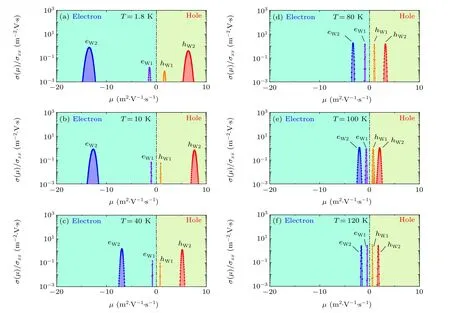
Fig.1. The MS of TaAs displayed in semi-logarithmic scale for temperature of(a)1.8 K,(b)10 K,(c)40 K,(d)80 K,(e)100 K,and(f)120 K.

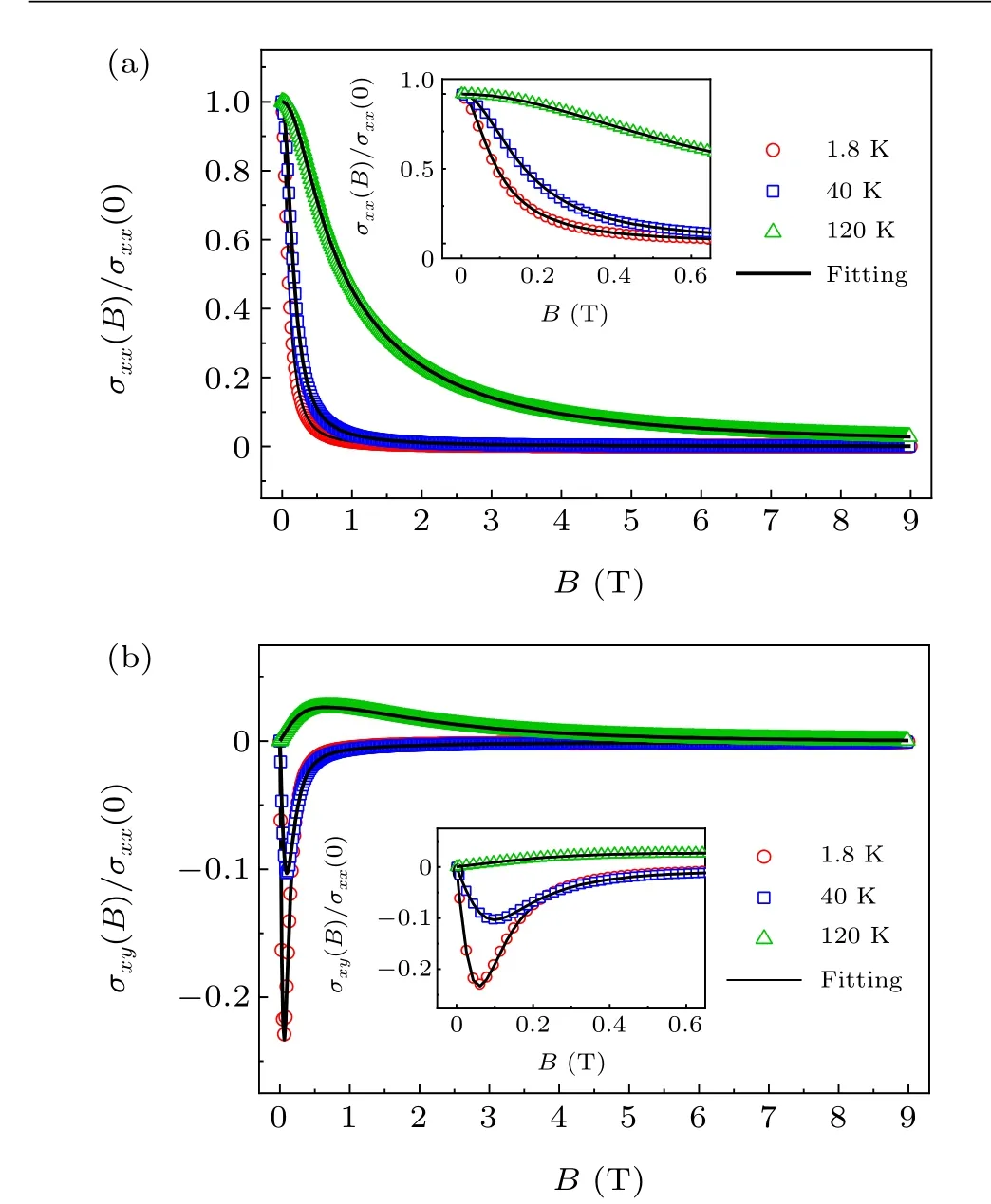
Fig.2. Normalized experimental magnetic conductivity(a)σxx(B)/σxx(0)and(b)Hall conductivity σxy(B)/σxx(0)at 1.8 K,10 K,40 K,80 K,100 K,and 120 K(dots),and its MEMSA fitting(solid lines).

3.2. Temperature dependence of mobility,carrier density,and conductivity contributions

To further explore the temperature dependence of MS,we calculate the mobilities, carrier densities, and conductivity contributions from MS and present them in Figs.3(a)–3(c).

The mobilities for each type of carriers are calculated by taking the peak values. At the lowest temperatureT=1.8 K, for W1 fermions,eW1has a very high mobility(μeW1= 13.44 m2·V-1·s-1), which is close to the mobilities of Dirac fermions in Dirac materials such as graphene(μ=20 m2·V-1·s-1), and is slightly smaller than the value estimated by SdH oscillation (μ= 18 m2·V-1·s-1).[7]The mobility ofhW1is lower (μhW1=1.64 m2·V-1·s-1), but it is still much larger than the mobility of carriers in silver, and is close to Dirac-like fermions in PtBi2.[20]For W2 fermions,the mobility ofhW2μhW2=6.39 m2·V-1·s-1, which is about half ofμeW1, whereas that ofeW2,μeW2=1.36 m2·V-1·s-1,which is comparable toμhW1. When changing the temperature, as shown in Fig. 3(a), low mobility fermions, i.e.,μeW2andμhW1, are almost temperature independent. For high mobility fermions,i.e.,μeW1andμhW2,on the contrary,in general,the mobility decreases significantly with increasing temperature, except thatμhW2increases slightly atT=10 K.The decrease of mobilities for W2 is probably due to increased thermal scattering.μeW1decreases faster thanμhW2forT ＜80 K,butμeW1≈μhW2forT ＞80 K, which is consistent with the symmetric MS shown in Figs.1(d)–1(f).

In Fig. 3(b), we show carrier densities as a function of temperature. Carrier densities for mobilityμ ∈[a,b] can be calculated by

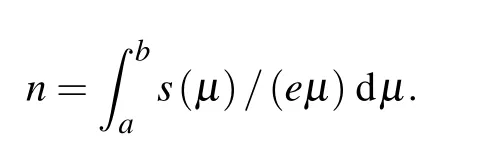
By takingaandbto be the lower and upper boundary of a specific peak,this integral gives its carrier density. ForT ＜40 K,the carrier densities of big peaks,i.e.,neW1foreW1andnhW2forhW2, are almost independent of temperature, and their values are 2 orders less than many other reported large magnetoresistance topological materials,such as pyrite PtBi2,[20]WTe2[22]and LaSb,[23]but are similar to Cr3As2.[24]The charge densities for the two small peaks(neW2foreW2andnhW1forhW1)are 1 order smaller.

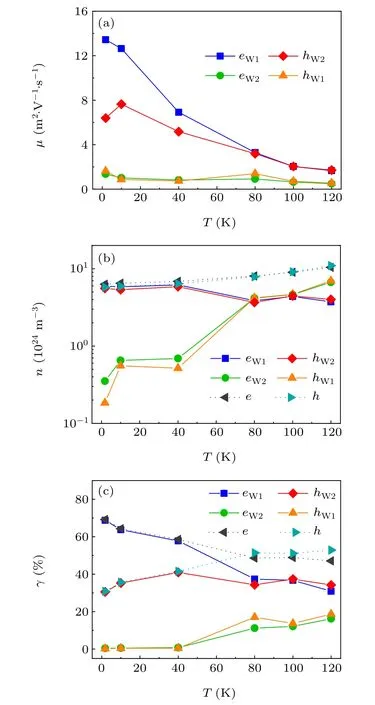
Fig.3. (a)The temperature dependence of mobilities μ,(b)carrier densities n,(c)RCC at zero field γ.

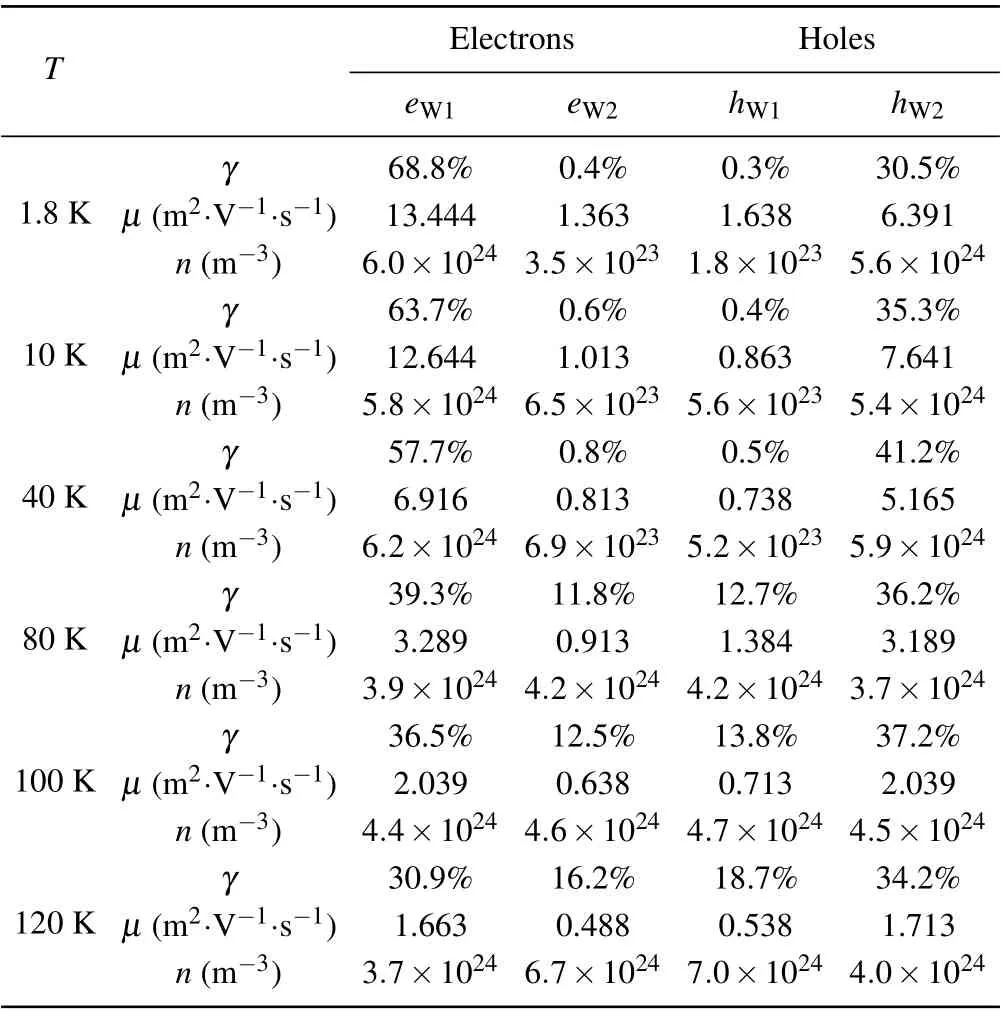
Table 1. Summery of carrier information: contribution to the conductivity γ,average mobility μ,and change concentration n.

3.3. Field dependence of the conductivity contribution

To analyze the ultra-high MR of TaAs, we calculate the field dependence ofσxxfor each peak by substitutings(μ)of each peak back to Eq. (1). ForμB ≫1,σxx∝(μB)-2≈0.Therefore, the initially dominated high mobility carriers will be localized after increasing field,while the localization of the low mobility carriers is weak. As a result, low mobility carriers become dominant. This behavior leads to a crossover of the conductivity contribution as a function of field for different bands. If an initially hole-dominated conductivity becomes electron-dominated at a high field(vice versa),the Hall conductivity sign changes. For complex MS,the sign change can even appear more than once. If ultra-high mobility carriers dominate the conductivity(e.g.,our TaAs sample at low temperature), even a very low field is capable of localizing the conducting carriers, thus, greatly decreasing conductivity, causing a field-induced conductor to insulator transition(CIT),[25–28]and generating extremely large MR.

For TaAs, the conductivities of each type of carriers as a function of field are shown in Fig. 4. AtT=1.8 K, the ultra-high mobility ofeW1causes a very fast localization. As shown in Fig.4(a),the crossover of the conductivity contribution ofeW1, andhW2appears at a field as low asB=0.12 T(see the intersection ofσxxforeW2andhW2). This illustrates that the dominant carrier is the electron-like W1 fermion whenB ＞0.12 T,but it is the hole-like W2 fermion whenB ＞0.12 T.Therefore,the Hall conductivity sign changes. For a high field limit,σxx(B)≈[σxx(0)μ-2]B-2=KB-2, whereKis a parameter that determines dominant carriers at high field. Therefore, due to the extremely lowσxx(0) of thermal-activated fermions, theirKvalue is always smaller than that of the preexisting fermionseW1andhW2. Therefore, the thermalactivated fermions always have a lower contribution to the conductor for various fields.

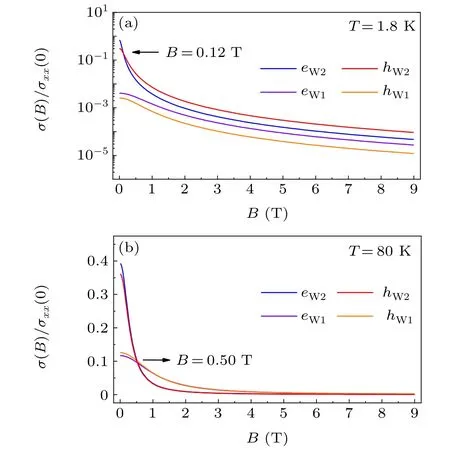
Fig.4. (a)The conductivity contributions vary with the magnetic field for T =1.8 K(a),and T =80 K(b),respectively.

At 80 K, as was discussed previously, the mobility and density of the electron equals that of the hole for both W1 and W2. Therefore, theσxx(B) of the electron always overlaps with the hole(see Fig.4(b)),so we cannot easily identify the dominant carrier between the electron-like and hole-like carriers. However, compared with the low temperature case,the conductivity for thermal-activated fermions is greatly enhanced. Due to their low mobilities, theirKvalues become larger than those of preexisting fermions. Therefore,an intersection ofσxx(B)for thermal-activated fermions and preexisting fermions appears (atB=0.5 T), indicating that the preexisting fermion-dominated conductivity becomes thermalactivated-fermion dominant whenB ＞0.5 T.

4. Conclusion

In summary,we use MEMSA to study the carrier properties of the type-I Weyl semimetal TaAs by fitting the experimentally measured longitudinal and transverse electric transport curves. At low temperature, we discovered four peaks:two big peaks and two small peaks(each containing one electron peak and one hole peak). Upon increasing the temperature, the two small peaks grow, showing that they are thermal-activated fermions. By comparing with reported firstprinciples results,the following peaks are identified: big electron peak and the small hole peak correspond to Weyl-I and the other two correspond to Weyl-II.Further quantitative calculation of mobility,carrier density,and RCC for varying temperatures shows that at low temperatures, the two dominant peaks have very high mobilities,which decrease with increasing temperature, whereas the carrier densities are insensitive to temperature change untilT ＞40 K. However, the carrier densities of the two small peaks quickly increase with temperature,indicating that they are thermal-activated fermions. The increased carrier density also increases their RCC.Our results explain the Hall sign change phenomenon,and shows the origin of non-saturating magnetoresistance.

Acknowledgment

Project supported by the National Natural Science Foundation of China (Grant Nos. 11674054, U1932217, and 11704067).