New Approach to Calculate the Unavailability of Identical Spares in Cold Spare Configuration

NYAN Win-aung, WEI Hai-jun(魏海军),2*, LIU Ting(柳 霆)

1 Marine Engineering College, Dalian Maritime University, Dalian 116026, China 2 Marcent Marine College, Shanghai Maritime University, Shanghai 200315, China

New Approach to Calculate the Unavailability of Identical Spares in Cold Spare Configuration

NYAN Win-aung1, WEI Hai-jun(魏海军)1,2*, LIU Ting(柳 霆)1

1MarineEngineeringCollege,DalianMaritimeUniversity,Dalian116026,China2MarcentMarineCollege,ShanghaiMaritimeUniversity,Shanghai200315,China

Cold spare is the most common configuration amongst the three types of configuration for systems used on board and for power generation systems. A new approach to calculate the unavailability of systems composed of identical spares in cold spare configuration was proposed in this study. Instead of using the spare gate of dynamic fault tree(DFT) and the Markov analysis, AND gate of static fault tree used for calculating the unavailability of cold spare systems was proposed in this paper. By using this approach, unavailability of identical cold spare systems composed of non-repairable spare components can be calculated exactly and systems composed of both repairable and nonreparable identical spare components can be estimated without building large Markov state diagram.

coldspare;sparegate;ANDgate;failurepercentage(FP);faulttreeanalysis;Markovanalysis

Introduction

Based on the dormancy factor of spares, spares can be classified as hot, cold, and warm spares. Calculation of the reliability properties of hot spares is the simplest and its calculation is the same as AND gate of static fault tree calculation. The dynamic fault tree (DFT) method of analysis such as an analytical method (Markov analysis) is required to deal with the cold and warm spares. Researchers provided different methods to solve cold and warm spares. Besides the applying of Markov analysis[1-2]to solve DFT, Monte Carlo simulation[3], analytical approach[4], Bayesian network approach[5], conditional probability approach[6], numerical simulation approach[7]， and other approaches which applied logic gates[8-9]are proposed by researchers to solve dynamic gates of fault tree including spare gate. Among the three types of spare configuration, identical cold spares are commonly met in systems applied on board such as the ship propulsion system and the electric power generation system. Spares in these systems are well maintained and fully monitored and powered up only on demand. In this study, exact and approximate methods to calculate the unavailability of identical cold spares with exponential failure distribution (constant failure rate) are discussed in detail with their limitation.

1 Relation between AND Gate and Spare Gate

Unavailability of using two identical components in an AND gate can be generally calculated by using Eq. (1)[10].

Q=(1-exp(-λtPF))2,

(1)

whereQis unavailability;λis the failure rate;tis time; andPFis failure percentage, which is egual to 100%.

Failure percentage (PF) in AND gate is 100% and the result of AND gate is the same as the result of hot spares in spare gate calculation of DFT. If the spare types are cold spare, their unavailability cannot be calculated by using Eq. (1). Generally analytical method (Markov analysis) is used to solve cold spare gates. The unavailability of cold spares is less than hot spare and the trend of changing unavailability of two identical cold and hot spares with failure rate 0.001 per hour can be seen in Fig.1.

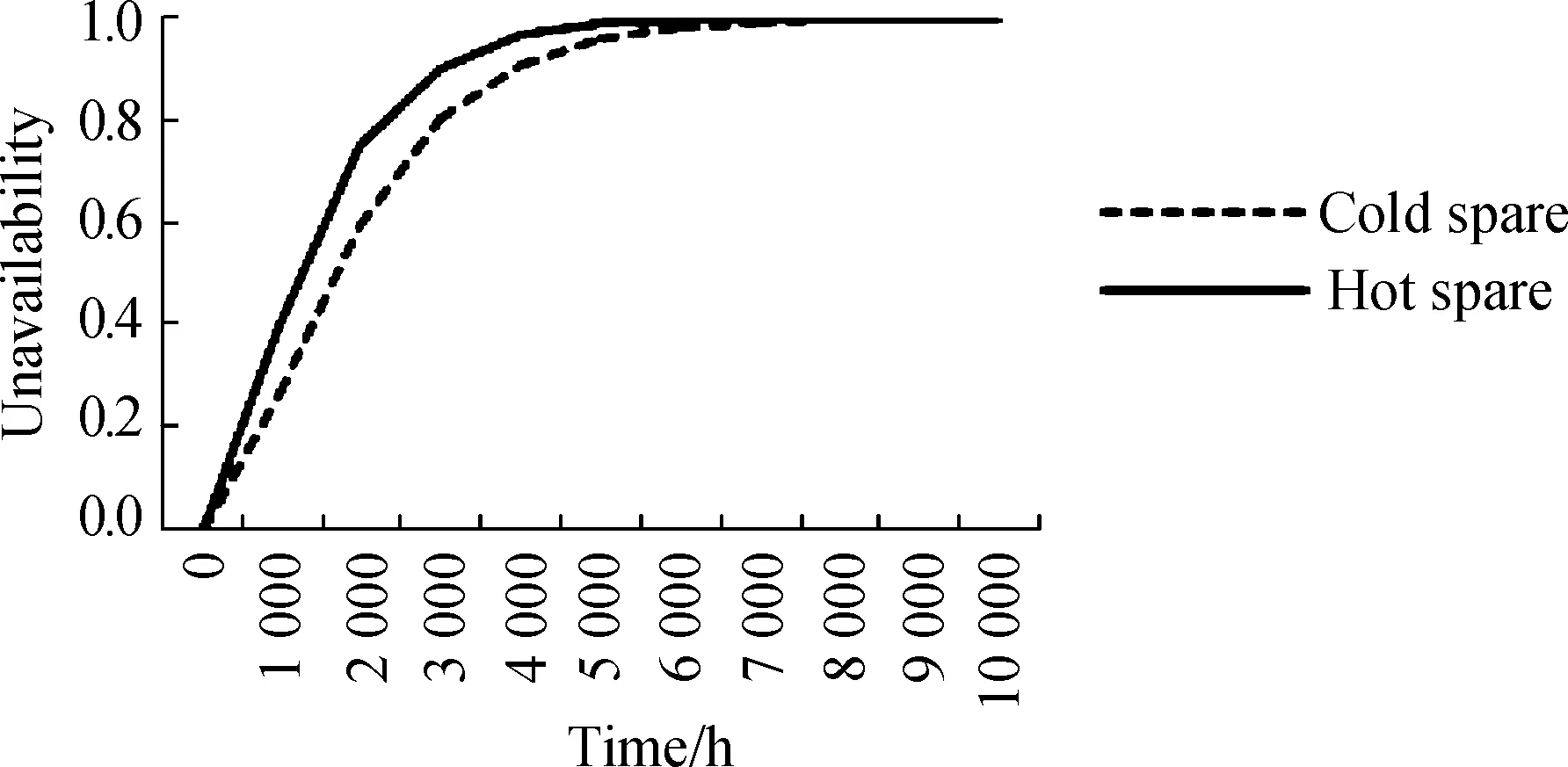
Fig.1 Unavailability of two identical components in cold and hot spare configuration

Markov diagrams for solving two identical components in cold and hot spares are shown in Fig.2. Markov analysis method is used to calculate the unavailability of cold and hot spares and their unavailability can be computed by using Eqs. (2) and (3). Both diagrams have three states. Hot spare transfers from one state to another by two transitions and cold spare by only one transition. All transitions have the same failure rate. The idea present in this calculation is to calculate the cold spare by using hot spare model and then change to simple AND gate calculation. Unavailability of hot spares can be calculated by using Eq. (1) which can avoid the high cost of calculation especially for the higher number of spares.

Q(t)=(1-e-λt)2，

(2)

Q(t)=1-(e-λt(λt+1)).

(3)

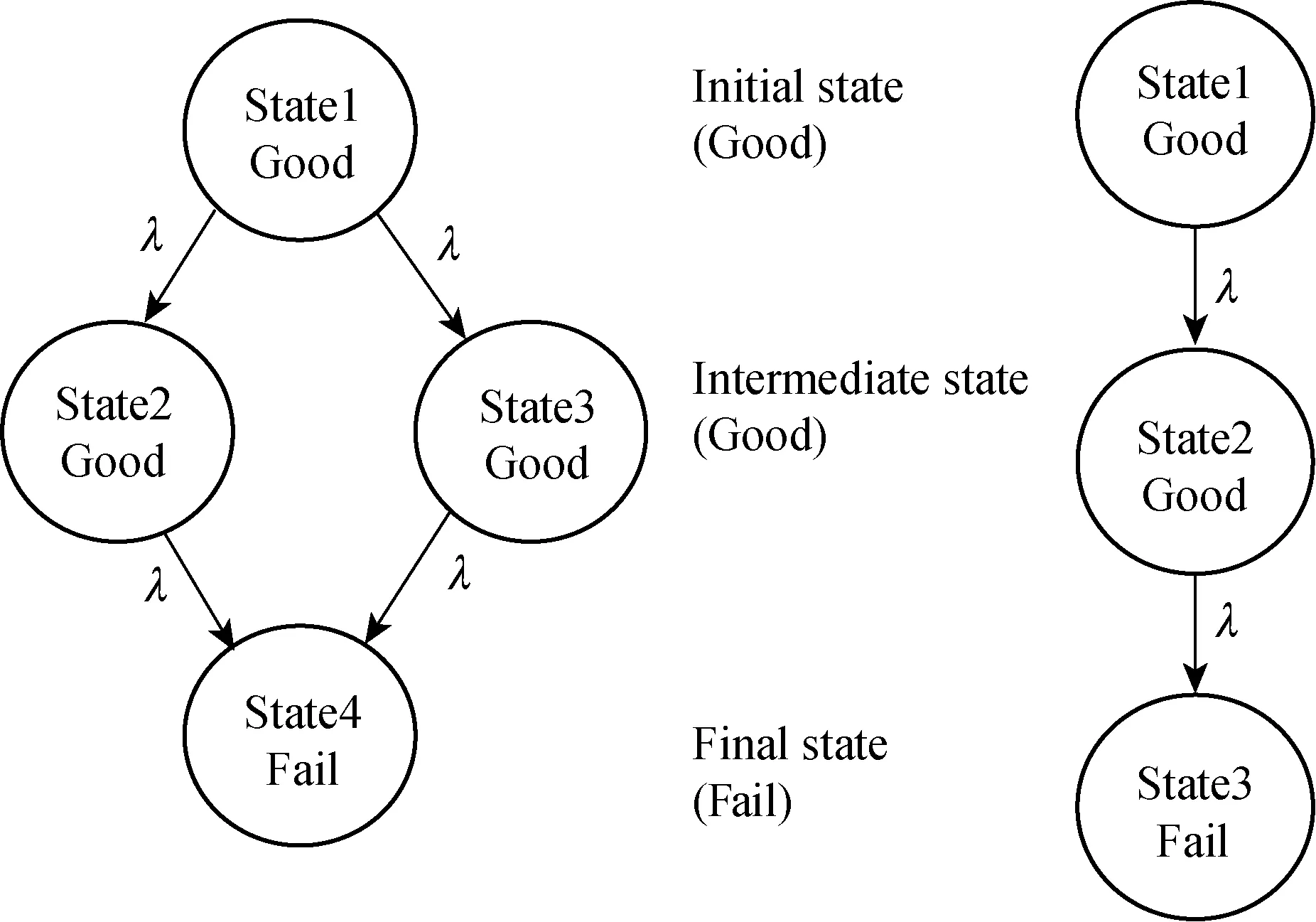
Fig.2 Markov diagram of two identical components in hot spare and cold spare

One transition in cold spare is attempted to replace by two transitions of hot spare by changing the failure rate by multiplying a factor calledPFas shown in Fig.3. Equation for calculating thePFfactor of two identical spares can be derived by using Eqs. (3) and (4)[10-11]. Unavailability of two identical components in cold spare configuration can be calculated by Eq. (4) and thePFrequired to use in Eq. (4) can be calculated by Eq. (6).

Fig.3 Markov diagrams of two identical components in cold spare

Equation for unavailability of cold spare configuration

Q(t)=(1-e-λPFt)2,

(4)

Q(t)=(1-(e-λPFt))2=1-(e-λt(λt+1)),

(5)

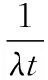
(6)

As an example, a system is composed with two identical components with failure rate of 0.001 and operation time of 1 000 h in cold spare configuration. Unavailability of the system can be calculated by using Markov analysis and the idea proposed in the above paragraph. Equation (3) is used to calculate the unavailability of the system for Markov analysis method and Eq. (4) is used for the proposed method. The factor of failure percentagePFused in Eq. (4) can be calculated by using Eq.(6) and the summery of the result can be seen as follows: unavailability of the system calculated by using Markov analysis is 0.264 241, failure percentage of the components used in the system is 72.163 7%, and unavailability of the system calculated by proposed method is 0.264 241.

The exact answer of unavailability can be obtained only at the time of 1 000 h because thePFis changed with time and failure rate. But it was found that error percentage of the unavailability between these two methods for other operation times are very small. Comparison of the results of the proposed method and Markov method is shown in Fig.4.

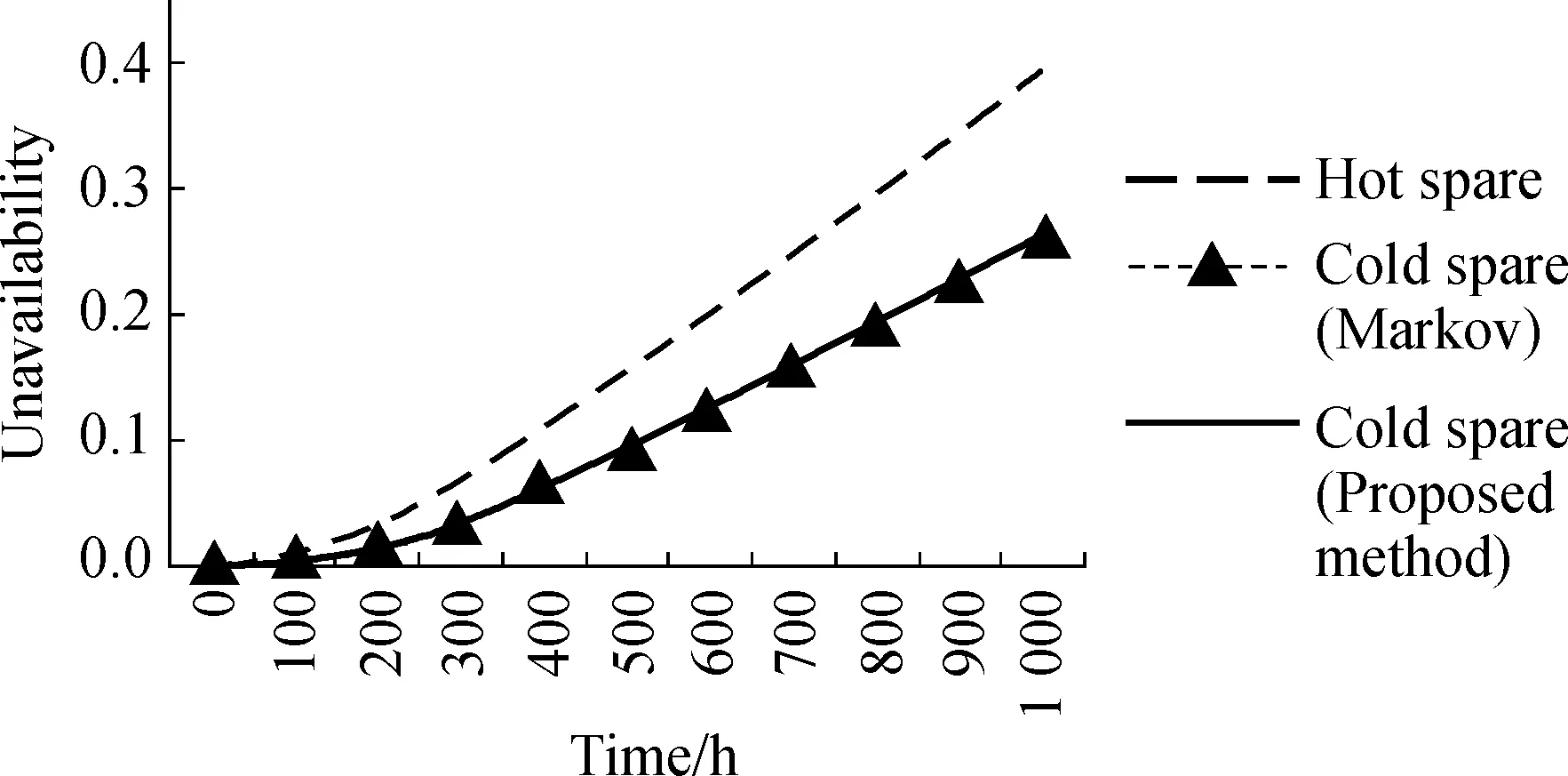
Fig.4 Comparison of the results of the proposed method and Markov analysis method

2 Calculation for the PF of More than Two Identical Components in Cold Spares

Calculation of thePFof more than two identical components in cold spares is undertaken as follows. Firstly the general formula for calculating the unavailability of “1+n” number of identical components in cold spares is derived from the Markov state diagram as shown in Fig.5 and equalized with the general form of Eq. (4) to calculate thePFof identical components in cold spare configuration. Derivation for the general formula for calculatingPFcan be seen as follows.

Fig.5 Markov diagram of “1+n” identical cold spares with failure rate λ

The general formula for unavailability of a component with different number of cold spare components can be driven out as follows

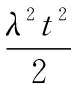
that is

(7)

whereiis the number of spare components.

The general formula for calculating the unavailability of “j” identical components using AND gate instead of using Markov analysis method can be shown by Eq. (8).

Qj(t)=(1-e-λPFt)j.

(8)

By applying Eqs. (7) and (8)PFof “j” identical components can be derived as follows:

(9)

whereiis the number of spare components,jis the number of identical components, andj=i+1.

PFfor different number of identical non-repairable components in cold spare configuration can be found by using Eq. (9). Unavailability of cold spare system can be computed by applying the outcomePFin Eq. (8). By using these two equations Markov state diagrams and differential equations are not necessary in the calculation of identical non-repairable components in cold spare configuration.

2.1 Limitation of general formula forPFcalculation

For extreme cases such ascomponents with very low failure rate and back up with more than one spares (for exampleλ=0.000 001 h-1, number of spares is 2), thePFfor calculating the unavailability of the system for a short operating time (for example,t=10 h), cannot be calculated by using the general formula. In a real world situation that kind of extreme case is rarely encountered and can be said to be nearly a zero percent possibility. Another extreme case is the opposite of the previous example. The use of the general formula is also inappropriate in the instance of a high failure rate and long operation time (for exampleλ=0.01 h-1,t=10 000 h). Both kinds of extreme cases are hardly ever encountered in the reliability analysis of systems.

2.2 Nature ofPFand its approximation

Two identical components in cold spare configuration with constant failure rate range from 0.01 to 0.000 001 per hour and operation time range of 10 to 10 000 000 h are used. Failure percentages for two identical components in cold spare configuration for different failure rate and operation time are calculated by using Eq. (9). Failure percentages used to calculate the unavailability of two identical components in cold spare configuration are shown in Fig.6. From the figure the higher the failure rate the failure percentage for calculating the unavailability of the system is nearly constant for long operation time. This fact can be more clearly understood by checking Table 1. From the table, the approximate values of the upper bound of the failure percentages of respective failure rate which are highlighted can be obtained.

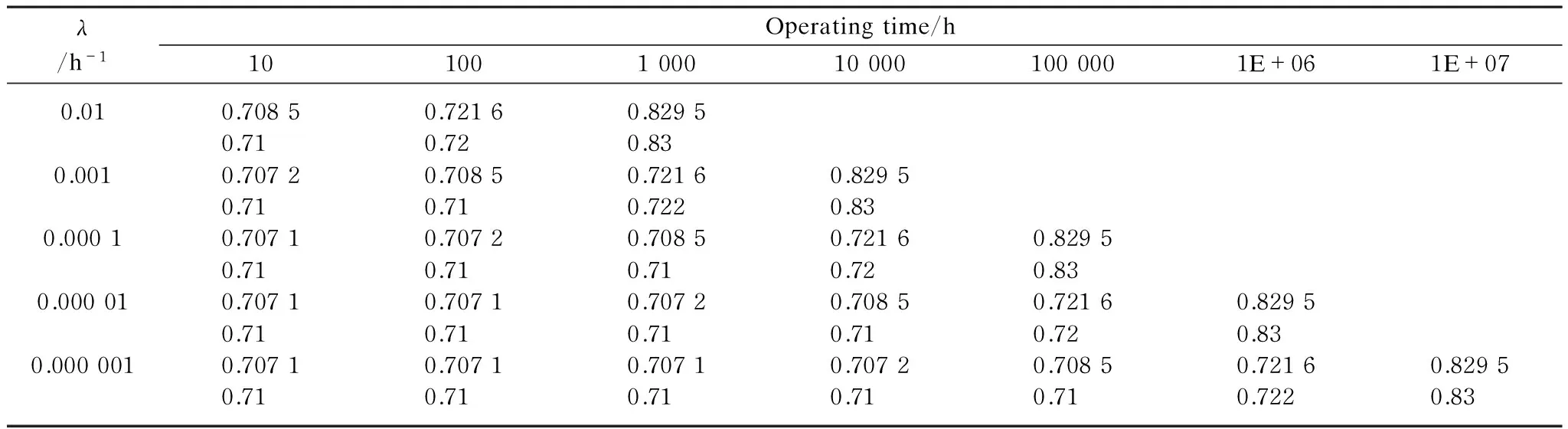
Table 1 Failure percentage of two identical components in cold spare configuration

By using the exact failure percentage obtained from Eq. (9) or the approximated value (upper bound value), unavailability of cold spare system with non-repairable identical components can be calculated or estimated by using conventional AND gate. But in real world situation spare is not only limited to a single component like a motor or a controller, it can be a sub system or the whole system, for example reduction gear system of ship propulsion system as shown in Fig.7. Systems are composed with more than one basic component, and these components can be both repairable and non-repairable. To calculate the unavailability of such a system, nature of cold spare configuration of repairable components needs to be considered. While failure rates of non-repairable components in a system can be combined and it can be calculated as a single non repairable component, failure rate of repairable components cannot be combined and need to be calculated individually for spare system calculation. The following section described the basic idea of approximating the unavailability of repairable component in cold spare configuration.

Fig.6 Failure percentage for different failure rate of two identical components in cold spare configuration

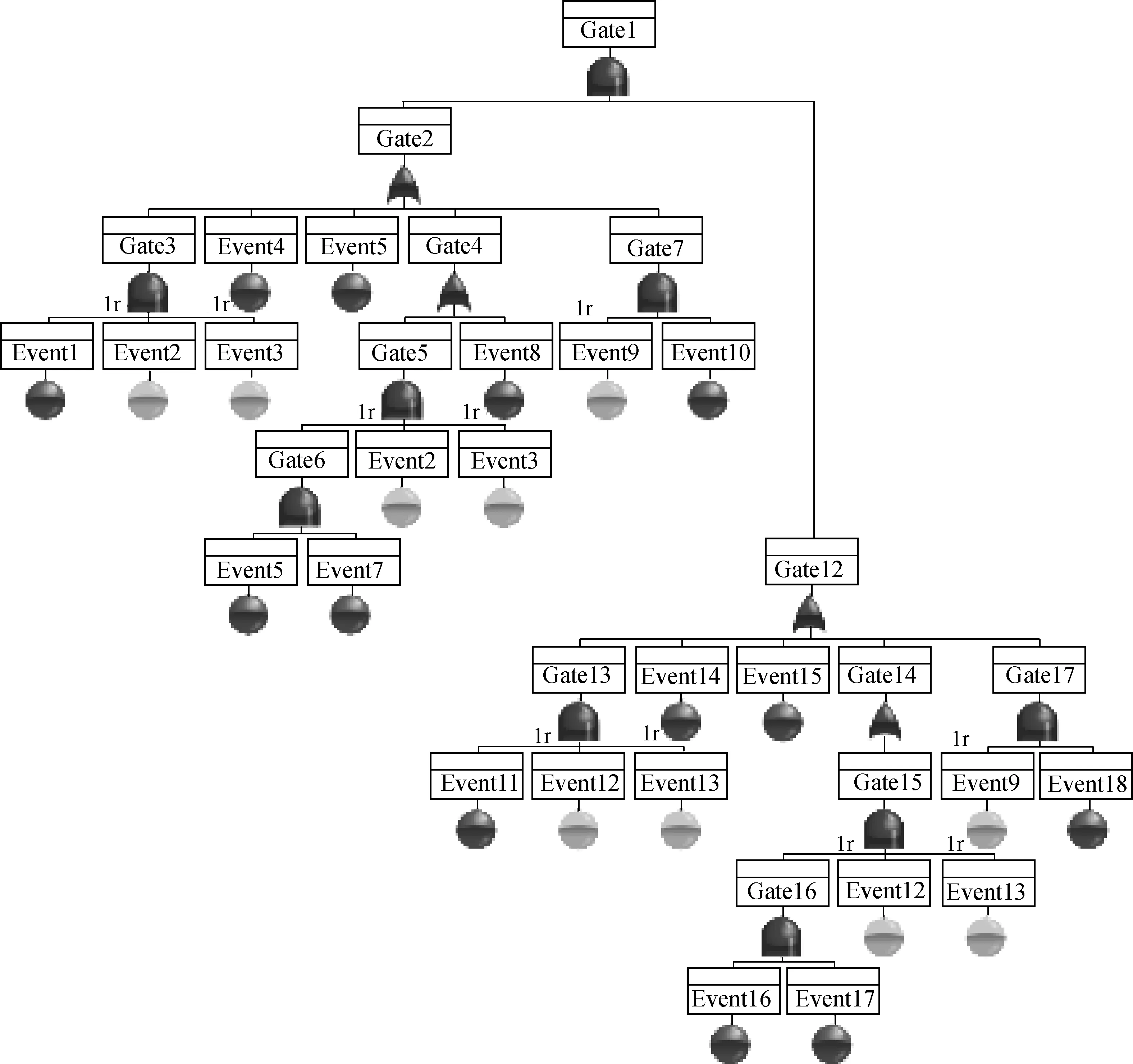
Fig.7 Fault tree diagram to compute the unavailability of two sets of reduction gear and propeller system in cold spare configuration by using proposed method

3 Criteria for Approximating of the Unavailability of Repairable Components in Cold Spare Configuration

Repairable components are high availability components in process especially with low failure rate and high repair rates. Basically there are four conditions of repairable components which depend on their failure rate and repair rates, and example of the respective failure rates and repair rates of the four different types of two identical repairable components are shown in Table 2. Markov analysis can be used to calculate the unavailability of two identical repairable components in cold spare configuration. For the two identical components in hot spare configuration both Markov analysis and AND gate function of reliability software can be used. The unavailability of two identical repairable spares in cold and hot spare configurations can be assumed to be the same in their steady state if the ratio of repair rate to failure rate is more than 100. In the real world situation this ratio is normally above 100 except for some extreme cases. Before reaching steady state there is a difference between two results and after reaching the steady state the difference is in negligible amount, as shown in Fig.8. In

the case of repair rate to failure rate ratio is above 100, after reaching the steady state the difference between the unavailability result of cold spare and hot spare configuration is about 1 percent of the unavailability value of the result of cold spare configuration. The higher the ratio of repair rate to failure rate is lesser error percentage between results. This error can be negligible in comparison with unavailability of other non-repairable components in systems.

RepairrateRRFailurerateλLowHighLowHighλ=0.0001λ=0.01RR=0.001RR=0.001Unavailabilityofthesystemincoldspareconfigurationis0.009Unavailabilityofthesystemincoldspareconfigurationis0.8264Unavailabilityofthesysteminhotspareconfigurationis0.00826Unavailabilityofthesysteminhotspareconfigurationis0.9λ=0.0001λ=0.01RR=0.01RR=0.01Unavailabilityofthesystemincoldspareconfigurationis9.9e-5Unavailabilityofthesystemincoldspareconfigurationis0.33Unavailabilityofthesysteminhotspareconfigurationis9.8e-5Unavailabilityofthesysteminhotspareconfigurationis0.25

By using this proposed method, unavailability of cold spare configuration of systems which are composed of non-repairable components can be calculated exactly and systems which are composed with both non-repairable and repairable components can be estimated except in a few extreme cases. The main idea of application of the proposed modified fault tree method can be observed in Fig.9, whereRNis non-repairable,Ris repairable,λis failure rate,PFis failure percentage, andRRis repair rate.

As a case study, the unavailability of the two sets of reduction gear and propeller system of USNS supply is computed by using proposed method and conventional Markov analysis method and compared results to validate the approach for use in real world system[12-13].

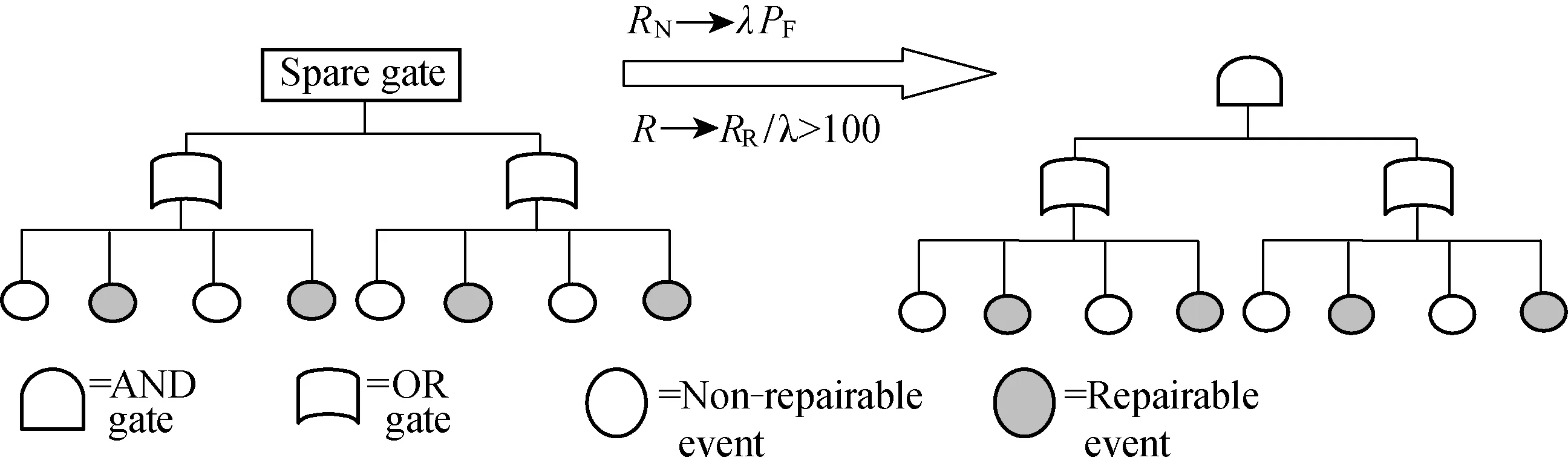
Fig.9 Proposed idea of transforming from spare gate to AND gate

4 Case Study of the Computing the Unavailability of Two Sets of Reduction Gear and Propeller System in Cold Spare Configuration

The reduction gear and propeller systems are one of the important parts of the marine propulsion system. There are two sets of reduction gear and propeller systems in the propulsion system of USNS supply. The main task of the reduction gear system is to reduce the high revolution of gas turbine and transmits it to fix propeller through shaft. The fault tree diagram of a reduction gear and propeller set drawn by using Relex software can be seen in Fig.10 and failure and repair data are shown in Table 3.

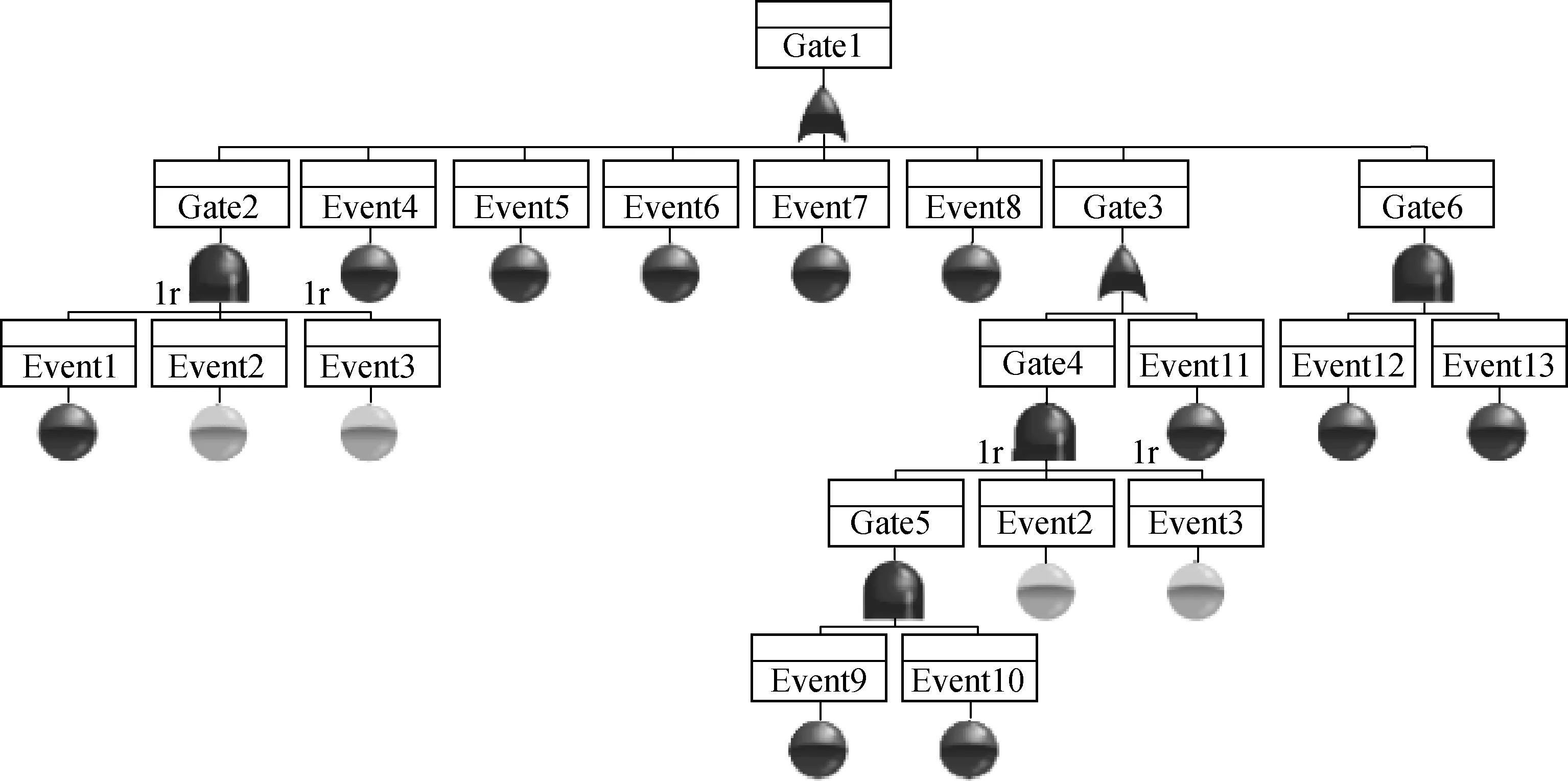
Fig.10 Fault tree diagram of reduction gear and propeller system

EventNo.Descriptionλ/(10-6·h-1)Repairtime/h1Reductiongearlubeoilservicepumpattached129.575.92Reductiongearmotordrivestandbylubeoilpump(repeated)270.2733Reductiongearmotordrivenemergencylubeoilpump(repeated)270.2734Mainreductiongear(reversing)48.0713.35Mainreductiongear(reversing)(non-repairable)5Non-repairable6Bearing/seal(non-repairable)4.348Non-repairable7Shafting(non-repairable)4.348Non-repairable8Fixedpitchpropeller(non-repairable)5Non-repairable9FRANCO-TOSImotordrivenemergencylubeoilpump270.27310FRANCO-TOSImotordrivestandbylubeoilpump270.27311RCClubeoilcooler11.111312Maincontrolconsole(repeated)34.4831713LocalshaftcontrolUnit11001

First conventional Markov analysis is used to calculate the unavailability of cold spare configuration of two sets of reduction gear and propeller systems for the operation time of 3 000 h. Markov diagram for the cold spare configuration of the reduction gear systems is shown in Fig.11. Detail descriptions of the states are described in Table 4. It has 71 states and needs to use 71 differential equations to solve the problem. Matlab program is used to calculate the unavailability of the cold spare configuration[14]. Deriving 71 equations from the Markov diagram is time consuming work and error prone during the construction of the equations. Matlab ODE 45 function is used to solve these differential equations and the unavailability of the cold spare configuration of the system is calculated by using Eq. (10) and the results calculated by using Markov analysis methods are shown in Table 5.

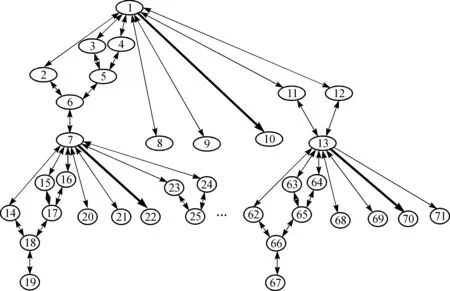
Fig.11 Markov diagram of the two sets of reduction gear and propeller system in cold spare configuration

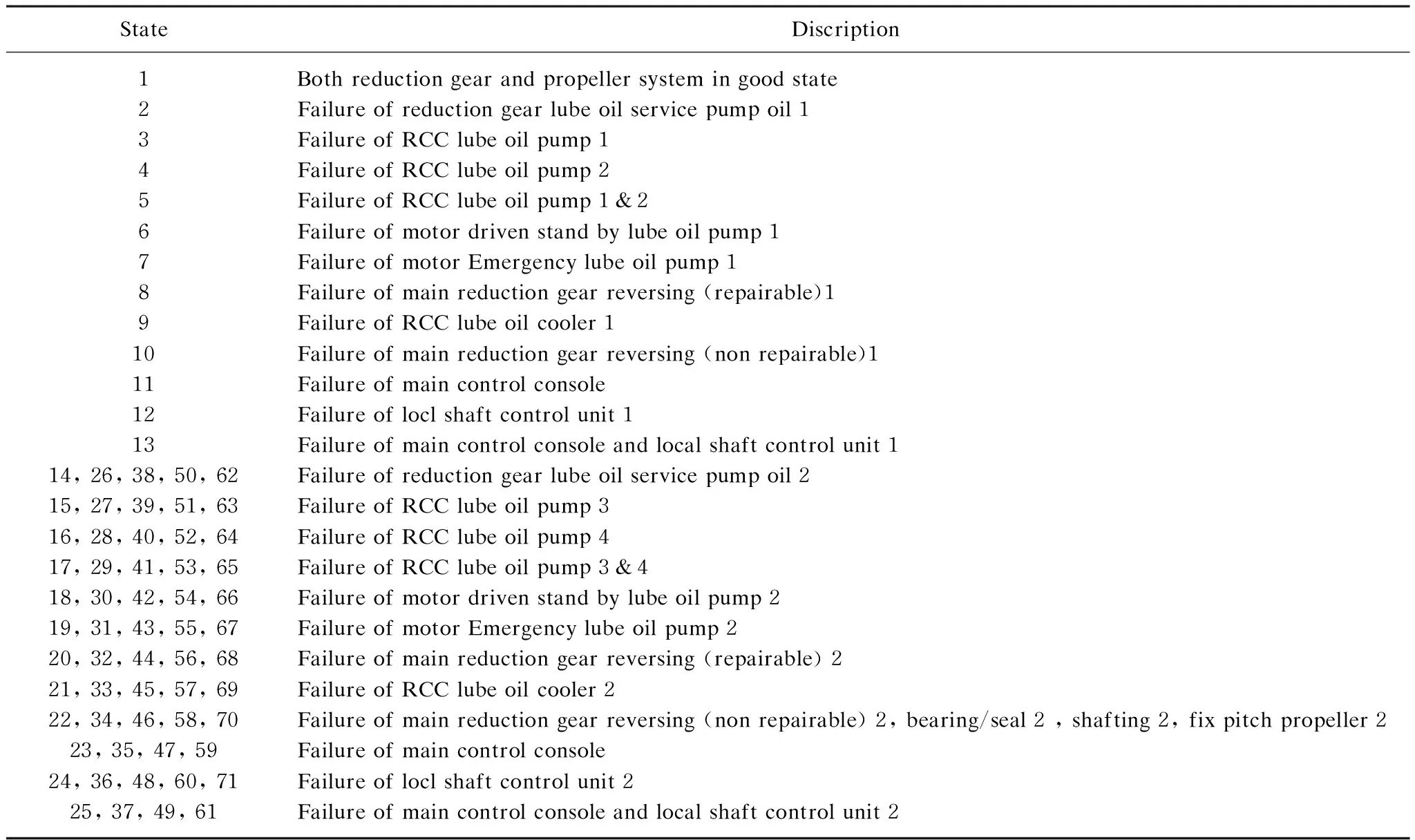
StateDiscription1Bothreductiongearandpropellersystemingoodstate2Failureofreductiongearlubeoilservicepumpoil13FailureofRCClubeoilpump14FailureofRCClubeoilpump25FailureofRCClubeoilpump1&26Failureofmotordrivenstandbylubeoilpump17FailureofmotorEmergencylubeoilpump18Failureofmainreductiongearreversing(repairable)19FailureofRCClubeoilcooler110Failureofmainreductiongearreversing(nonrepairable)111Failureofmaincontrolconsole12Failureofloclshaftcontrolunit113Failureofmaincontrolconsoleandlocalshaftcontrolunit114,26,38,50,62Failureofreductiongearlubeoilservicepumpoil215,27,39,51,63FailureofRCClubeoilpump316,28,40,52,64FailureofRCClubeoilpump417,29,41,53,65FailureofRCClubeoilpump3&418,30,42,54,66Failureofmotordrivenstandbylubeoilpump219,31,43,55,67FailureofmotorEmergencylubeoilpump220,32,44,56,68Failureofmainreductiongearreversing(repairable)221,33,45,57,69FailureofRCClubeoilcooler222,34,46,58,70Failureofmainreductiongearreversing(nonrepairable)2,bearing/seal2,shafting2,fixpitchpropeller223,35,47,59Failureofmaincontrolconsole24,36,48,60,71Failureofloclshaftcontrolunit225,37,49,61Failureofmaincontrolconsoleandlocalshaftcontrolunit2

Q(t)= 1-[p1(t)+p2(t)+…+p18(t)+p23(t)+p24(t)+p26(t)+…+p30(t)+p35(t)+

p36(t)+p38(t)+…+p42(t)+p47(t)+p48(t)+p50(t)+…+p54(t)+

p59(t)+p60(t)+p62(t)+…+p66(t)].

(10)

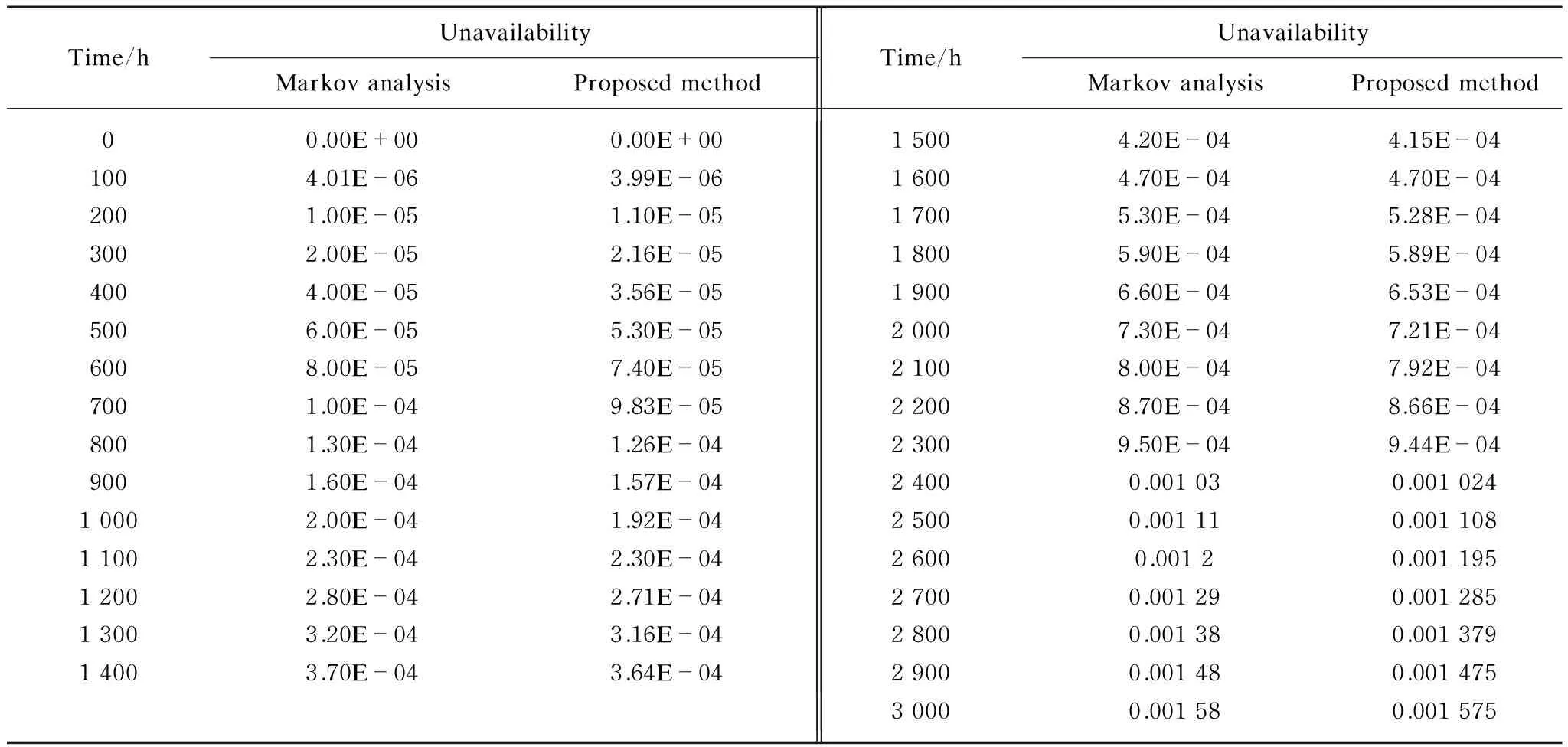
Table 5 Unavailability of the cold spare configuration of two sets of reduction gear and propeller system calculated by Markov analysis method and proposed method of modified fault tree

Secondly, the unavailability of two sets of reduction gear and propeller system in the cold spare configuration is calculated by the proposed method. Generally fault tree software such as Relex, Isograph, and Item[15-17]is used to compute large fault tree to avoid time consumption and mistakes. Software has limitations in using dynamic gates. Relex fault tree is used in this case study. Because of the limitations of spare gate of Relex fault tree, the cold spare configuration of reduction gear and propeller system cannot be computed directly.

In this case study, the proposed approach is used together with Relex fault tree to calculate the unavailability of the reduction gear systems in cold spare configuration. By applying the proposed method, unavailability of identical components or systems in cold spare configuration can be calculated by using AND gate of Relex fault tree software. Building large states of Markov diagram and solving high number of differential equations can be avoided by using the proposed method. The total failure rate of non-repairable components, main reduction gear reversing, bearing/seal, shafting, fix pitch propeller, can be computed by combining with the failure rate of these components and the total failure rate is 1.869 565E-5 per 106hour. The failure percentage of the combined failure rate of non-repairable components is calculated by using Eq. (9). In this case study failure percentage of 70.97% is used for the operation time of 3 000 h and that failure percentage is also used as an upper bond value for approximating for the unavailability for the operation time of 0 to 3 000 h. Fault tree diagram for this calculation is shown in Fig.7. As shown in Fig.7, AND top gate is used for calculating the unavailability of two sets of reduction gear and propeller system in cold spare configuration. The results are described in Table 5 and comparison between the results of Markov analysis and proposed modified fault tree method can be observed in Fig.12. To better understand about the effect of hot spare and cold spare configurations and clarify the result of the proposed method, the unavailability of the two sets of reduction gear and propeller system in hot spare configuration was computed by using Relex is also described in Fig.12.

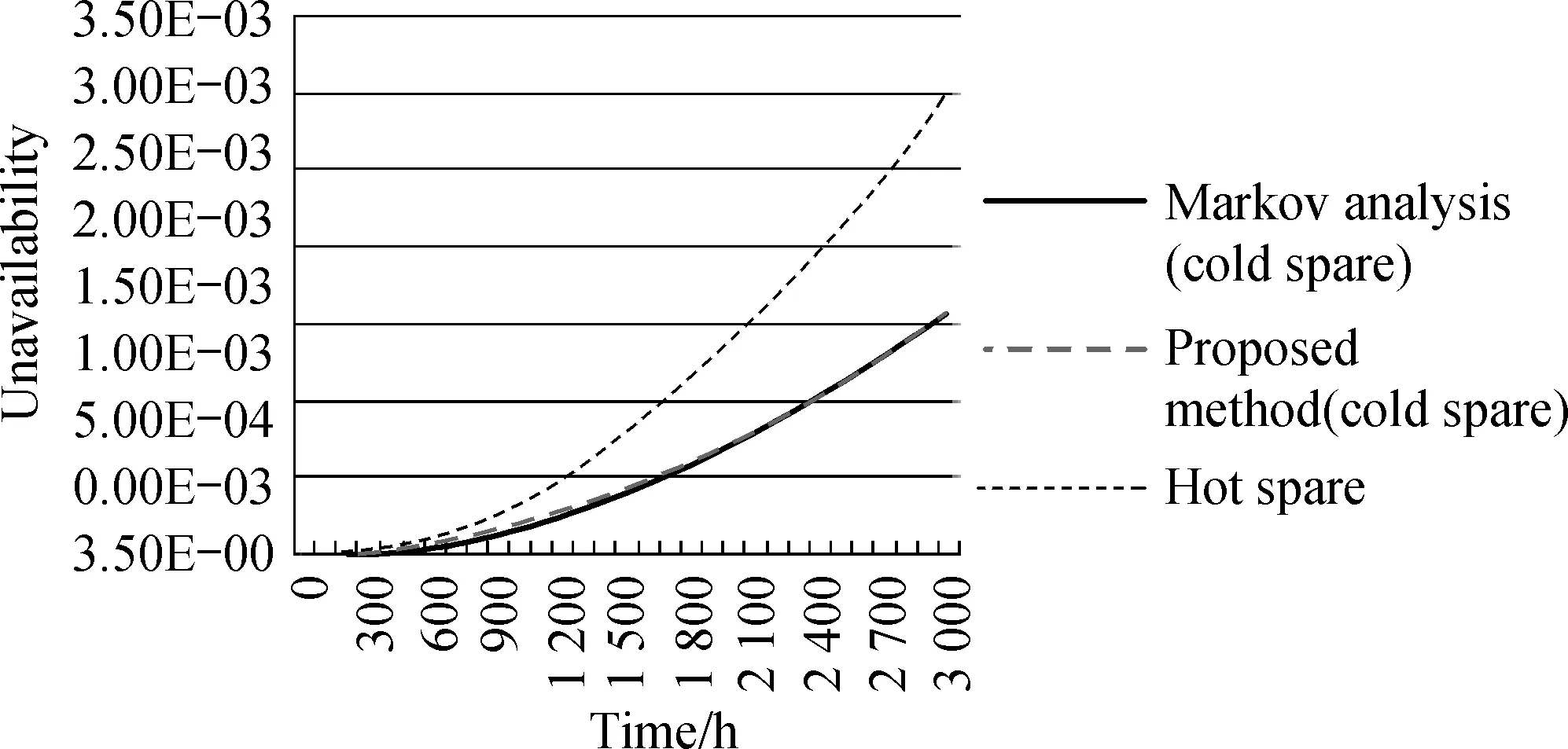
Fig.12 Comparison of the unavailability of two sets of reduction gear and propeller system in cold spare configuration, calculated by Markov analysis method and proposed method

From the results of Table 5, the error between the proposed method and Markov analysis method at the operation time of 3 000 h is less than 0.5% of the result obtained from Markov analysis. Therefore the proposed method is confirmed and validated in estimating of the unavailability of identical cold spares of real world systems.

5 Conclusions

In this paper a new approach is proposed to compute the unavailability of non-repairable identical cold spares without using the Markov analysis. An important criterion of repair rate to failure rate ratio is also proposed to estimate the unavailability of repairable components in cold spares by using AND gate. By applying the factor of failure percentage and criterion of repair rate to failure rate ratio of the proposed method, unavailability of systems composed of nonrepairable components and repairable components in cold spare configuration can be estimated by using fault tree AND gate. The main advantage of the proposed modified fault tree method is to reduce the cost of calculation and it’s capability to combine fault tree software to overcome the limitations of software in computing of unavailability of identical systems in cold spare configuration of real world system.

[1] Xing L, Amari S. Handbook of Performability Engineering [M]. New York: Springer-Verlag, 2008: 595-617.

[2] Gulati R, Dugan J B. A Modular Approach for Analyzing Static and Dynamic Fault Trees[C]. Proceedings of Annual Reliability and Maintainability Symposium, USA, 1997: 57-63.

[3] Chiacchio F.An Open-Source Application to Model and Solve Dynamic Fault Tree of Real Industrial Systems [C]. Proceedings of 5th International Conference on Software, Knowledge Information, Industrial Management and Applications (SKIMA), Italy, 2011: 1-8.

[4] Merle G, Roussel J M, Lesage J J. Analytical Calculation of Failure Probabilities in Dynamic Fault Trees Including Spare Gates [C]. Proceedings of European Safety and Reliability Conference, Rhodes, Greece, 2010: 794-801

[5] Dugan B.A New Bayesian Network Approach to Solve Dynamic Fault Trees [C]. Proceedings of Reliability and Maintainability symposium, Hilton Mark Plaza Alexandria, VA, USA, 2005: 451-456.

[6] Amari S, Dill G, Howald E. A New Approach to Solve Dynamic Fault Trees [C]. Proceedings of the Annual Reliability and Maintainability Symposium, Tampa, FL, USA, 2003: 374-379.

[7] Liang XF, Yi H, Zhang YF,etal. A Numerical Simulation Approach for Reliability Analysis of Fault-Tolerant Repairable System [C]. Proceedings of 8th International Conference on Reliability, Maintainability and Safety, Chengdu, China, 2009: 191-196.

[8] Aliee H, Zarandi H R. A Fast and Accurate Fault Tree Analysis Based on Stochastic Logic Implemented on Field-Programmable Gate Arrays [J].IEEETransactionsonReliability, 2013, 62(1): 13-22.

[9] Cheshmikhani E, Zarandi H R, Aliee H. Accelerating Accurate Fault Tree Analysis Using HW/SW Co-design[J].ReliabilityandMaintainabilitySymposium(RAMS), 2014, 1(6): 27-30.

[10] Ebeling C E.An Introduction to Reliability and Maintainability Engineering [M]. New York: McGraw-Hill Education, 1997.

[11] Willium J S. Probability, Markov Chain, Queues and Simulation [M]. New Jersy : Princeton University Press, 2009.

[12] Young R B. Reliability Transform Method, MSc. Dissertation [D]. Virginia:Virginia Polytechnic Institute and State University, 2003: 171-179.

[13] USNS Supply[EB/OL]. [2014-05-10]. http://en.wikipedia.org/wiki/USNS_Supply_%28T-AOE-6%29.

[14] Atkinson K, Han W, Stewart D. Numerical Solution of Ordinary Differential Equations [M]. New Jersey: John Wiley & Sons, Inc., 2009.

[15] Relex[EB/OL]. [2014-05-10]. http://www.ptc.com/products/windchill/quality.

[16] Isograph[EB/OL]. (2013)[2014-05-08]. http://www.isograph-software.com/.

[17] Item[EB/OL]. (2013)[2014-05-08].http://www.itemsoft.com/.

Foundation item: National High-Technology Research and Development Program of China (863 Program)(No. 2013AA040203)

1672-5220(2014)06-0863-07

Received date: 2014-08-08

*Correspondence should be addressed to WEI Hai-jun, E-mail: hxl@dlmu.edu.cn

CLC number: TH122 Document code: A