抑制低频横向振动的电动振动台参数优化

2022-05-16左曙光吴旭东冯朝阳

振动与冲击 2022年9期

左曙光，潘健，吴旭东，冯朝阳

(同济大学汽车学院，上海 201804)

车辆的整车、关键总成与零部件在路面载荷等激励下的可靠性与耐久性测试是实现产业化前的重要步骤[1-2]，电动振动台可用于模拟汽车零部件的真实载荷环境，具有波形好和控制方便等诸多优点，应用十分广泛[3-4]。本文研究的单轴电动振动台垂向为主振方向，但电动振动台台面上预先设计的螺栓孔位置固定且数量有限，安装形状和质量分布不规则的被测件时无法保证其完全没有偏心，通过前期试验发现，当振动台安装了某向偏心距为0.7 m、质量为83.14 kg的被测件模拟300 kg发动机存在19.4 cm偏心距的测试场景时，动圈驱动电流频率为115 Hz，取附加台面中心点位置垂向加速度幅值为1g的工况，计算得到该工况下的横向振动比已经超过了100%，横向加速度输出已经大于垂向加速度输出，完全不能满足使用要求。

孟繁莹[5]提出了某型电动振动台的横向振动问题，发现在频率为420 Hz、950 Hz、1 500 Hz及1 980 Hz时横向振动比较大，但并未研究如何解决这一问题。从电磁学原理及振动力学角度分析，当被测件存在偏载时:①导致动圈在工作气隙中发生偏心和倾斜，此时会受到额外的横向电磁力激励;②当被测件质量较大时会使电动振动台运动系统的整体质心发生明显的横向偏移，此时动圈受到的垂向电磁力会由于质心偏移而产生一个翻转力矩，当系统工作在横向的平移及翻转模态[6-7]等频率处时，在这两方面的激励下，便会产生较为剧烈的横向振动。由于仅通过夹具设计来减小安装被测件的偏心量会增加夹具设计难度，为了从根本上解决横向振动问题，对电动振动台进行优化设计是一种可行的思路，而优化设计又可以从电磁结构与参数优化以及系统模态规划两方面进行。

(1)电磁优化:国内外学者目前针对电动振动台及工作原理相似的电磁作动器进行电磁优化主要目标为提高垂向激振力。Paulitsch等[8]设计了一种轻量级的电磁激振器，应用电磁有限元分析及磁路参数优化，获得了一定输入功率下能满足3 N激振力需求的电磁激振器；Bueren等[9]提出了一种线性电磁激振器的设计与优化方法，通过磁路参数优化提高了激振器输出电磁力，获取了更好的使用性能；Botezan等[10]对永磁激振器进行了设计，应用有限元法分析磁场中的磁通密度在台体部分的分布，并对磁场进行优化，提高了激振力；Yang等[11]设计了一种新型电磁激振器结构，有效提高了气隙磁场磁通密度，提高了电磁激振力；Lee等[12]通过数值模拟法分析了直流电磁泵的电磁力分布规律及主要结构参数对电磁力的影响，最终对其几何与电学参数进行优化设计并提高了电磁阀的使用性能。可见，在电磁优化方面，目前学者们均只考虑了主振方向的性能，对于是否可以通过电磁优化抑制电动振动台横向振动目前尚无分析和研究。

(2)模态规划:目前主要优化目标为提高振动台一阶轴向伸缩模态等的模态频率，从而拓宽振动台的工作频带，改善工作性能。李红强[13]以提高动圈一阶轴向模态频率为目标，通过Nastran软件对动圈模型进行了结构动力学及参数灵敏度分析，最终通过优化获得了更优的动力学性能；程鑫[14]对三轴液压角振动台进行了无负载和带负载两种情况下框架结构的动力学性能分析，获得相应的模态共振频率，通过对框架结构的优化显著提高了外框的1阶自振频率；唐波等[15]对角振动台采用粒子群优化算法进行优化，优化目标为提高振动台运动系统的一阶扭振频率并减小转动惯量；Zhou等[16-18]通过对振动台支撑弹簧进行刚度和阻尼优化，选取合适的动圈骨架形状，最终扩大了振动台的工作频率范围，同时抑制了低频区域存在的共振峰；汪超等[19]及仝宁可等[20]也进行了相应优化研究来提高振动台的1阶模态频率。可见目前针对电动振动台横向振动的模态规划研究较少，但是，部分学者通过阻尼优化实现了对振动峰值的抑制，这一点可在电动振动台横向振动模态规划方面进行借鉴。

为了从优化设计角度解决电动振动台存在的低频横向振动问题，本文首先建立了能够反映横向振动的电动振动台机电耦合模型，并分析横向振动的激励来源与机理，提出了横向振动优化途径与入手点；其次，分析了电动振动台空气弹簧和钢片弹簧的主要参数对横向振动的影响规律；最后，提出了面向车用工况路面激励频段的电动振动台横向振动优化评价指标，基于带精英策略的快速非支配排序遗传算法(NSGA-II算法)，选取主要参数进行了电动振动台参数优化，并分析了优化效果。

1 反映横向振动的电动振动台机电耦合建模

为深入研究电动振动台的横向振动问题并进行参数优化，首先应建立能够综合反映电动振动台横向和垂向振动特性的机电耦合模型。

1.1 电动振动台机械结构

本文研究的电动振动台包括台体及运动系统两部分，其机械结构及运动系统如图1所示。电动振动台台体部分提供了驱动线圈运动的气隙空间和励磁磁场，其两侧各有2个空气弹簧支撑在刚性支架上；运动系统包括驱动线圈、筋板、台面和附加台面等，驱动线圈为铜制且为漆包线来保证绝缘性，其和镁铝合金筋板通过环氧树脂一体铸成，而附加台面通过24个螺栓与台面刚性连接。运动系统与台体有两处柔性连接:①筋板中心处的空气弹簧，支撑运动系统垂向运动，此处还有垂直导向杆，可以提高运动系统的横向运动刚度；②台面与台体之间间隔90°布置的4组径向钢片弹簧，用于抑制运动系统上部的横向运动和扭转运动；此外，附加台面的角点处则由4个空气弹簧支撑在刚性支架上。

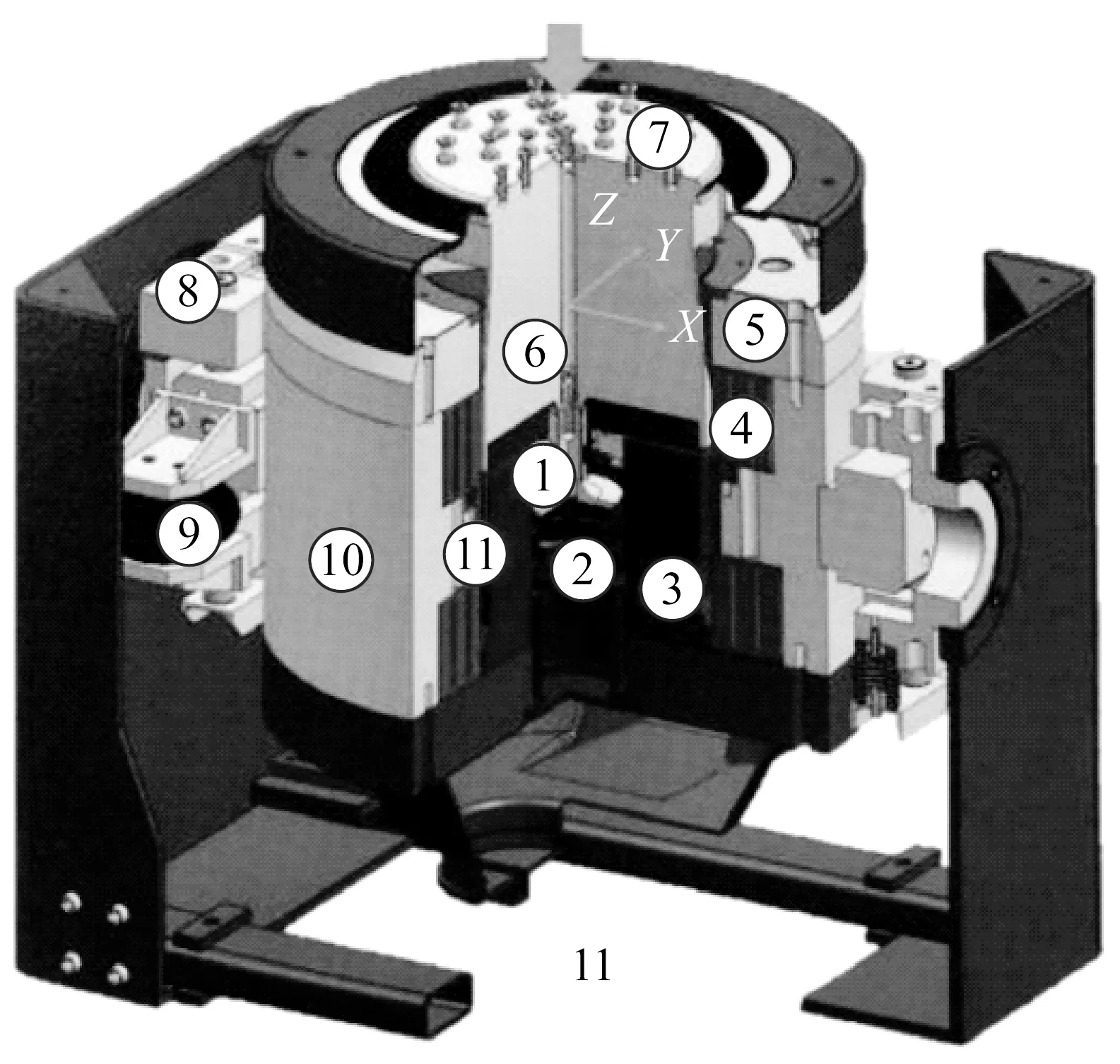
1.中心导杆;2.空气弹簧;3.中心磁极;4.励磁线圈;5.磁槽盖;6.筋板;7.台面;8.限位杆;9.台体空气弹簧;10.外磁环体;11.驱动线圈。

1.2 电动振动台机电耦合建模

本文电动振动台附加台面及坐标系设定如图2所示，机电耦合建模针对图2中电动振动台存在沿x方向偏载被测件的情况进行，图中x1位置被测件偏载距离为0.7 m，被测件质量为83.14 kg。前期研究发现电动振动台的横向振动主要由运动系统的翻转模态和横向平移模态贡献，因此考虑电动振动台系统如下4个自由度：运动系统沿x轴方向的平移运动x、运动系统沿z轴方向的平移运动z、运动系统绕y轴方向的翻转运动θy以及台体沿z轴方向的平移运动zb，台体质量较大，且有刚性限位杆约束其横向运动，因此仅考虑其垂向自由度。

图2 附加台面被测件示意图

对于该型电动振动台，前期研究已经发现[21]，电动振动台动圈径向等效电磁力对横向振动的贡献几乎可以忽略，横向振动的主要激励来源为动圈垂向等效电磁力引起的翻转力矩。因此，为了方便进行后续电动振动台优化研究，忽略动圈径向等效电磁力及动力学模型中影响较小的非线性项，建立如式(1)所示的电动振动台机电耦合模型，附加台面中心点横向和垂向加速度输出如式(2)所示，模型主要参数如表1所示。

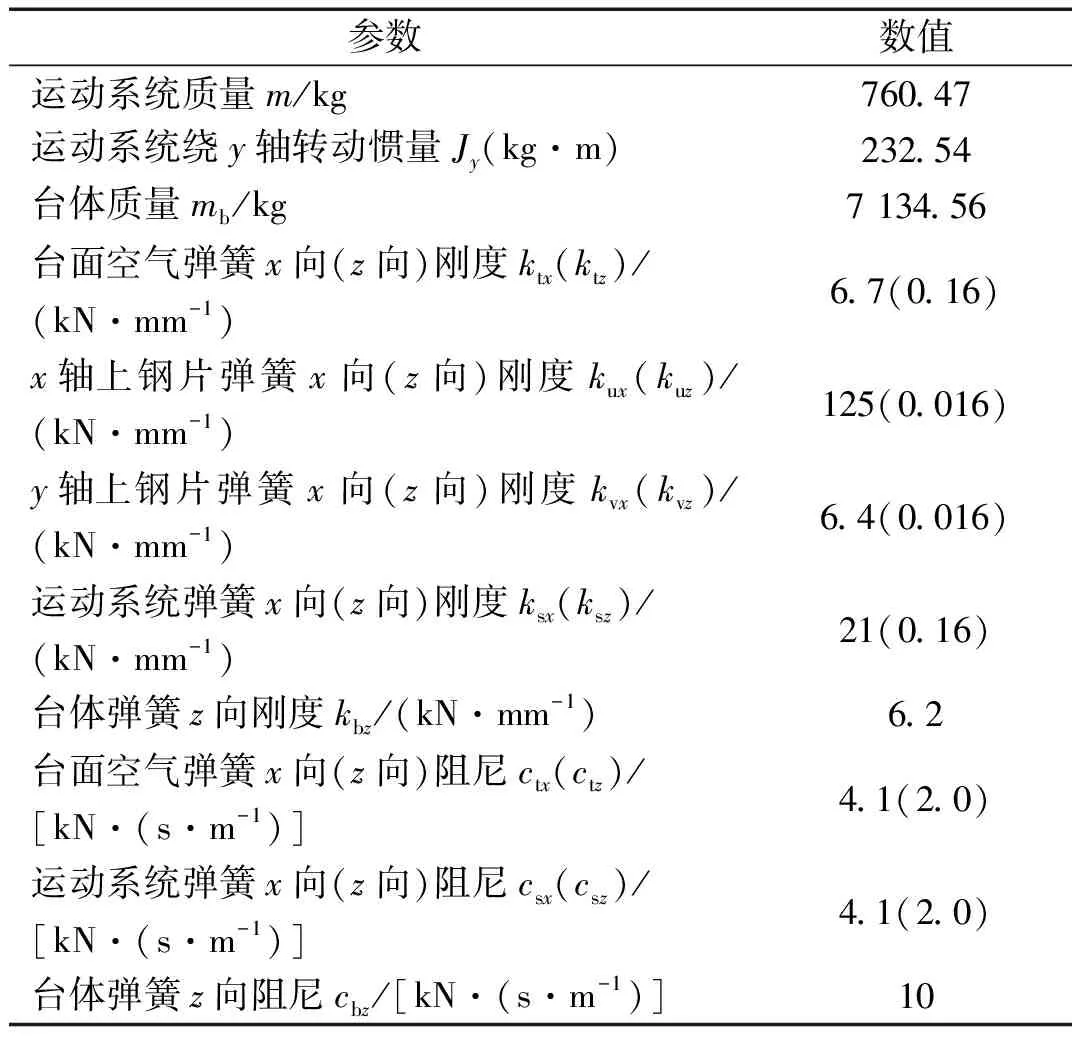
表1 模型主要参数

[4ktxΔzt-2(kux+kvx)Δzuv-ksxΔzs]θy-

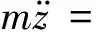
2kvz+ksz)zb+(4ktz+2kuz+2kvz+ksz)Δx0θy-

ksxΔzs]x+(4ktz+2kuz+2kvz+ksz)Δx0z-

2kvz+ksz+4kbz)zb-(2kuz+2kvz+ksz)Δx0θy+

(1)

(2)

式中：Δzt为运动系统质心与台面空气弹簧的z向距离；Δzuv为运动系统质心与钢片弹簧的z向距离；Δzs为运动系统质心与其支撑弹簧的z向距离；Δzg为运动系统质心与台面上表面的z向距离；Δx0为运动系统质心与系统中心的x向距离；Δxt为台面空气弹簧与系统中心的x向距离；Δxu为x轴上钢片弹簧与系统中心的x向距离；FI为与动圈驱动电流成正比的垂向等效电磁力。

1.3 电动振动台频响特性分析及模型验证

基于该机电耦合模型，以电动振动台附加台面中心点x向及z向加速度为输出，进行系统频响特性分析，并与试验结果对比，结果如图3所示。

由图3可知，本文建立的电动振动台四自由度机电耦合模型可以反映试验中电动振动台系统的横向及垂向输出特性，此外，该电动振动台x向加速度输出频响在20 Hz及113.5 Hz存在明显的共振现象，通过进行系统模态试验分析，z向频响函数中的共振峰对应电动振动台运动系统的z向平移模态，x向频响函数中20 Hz及113.5 Hz频率分别对应电动振动台运动系统的绕y轴翻转模态频率及x向平移模态频率，由于横向共振而导致了在这两个频率点处产生剧烈的横向振动。

(a)z向

进一步分析电动振动台的横向振动参数优化思路，从横向振动激励源角度，由于横向振动的激励源为动圈垂向等效电磁力引起的翻转力矩，减小电动振动台动圈的垂向等效电磁力会同时影响到电动振动台的垂向输出特性，整体来说并不会减小电动振动台的横向振动比；由于电动振动台在偏载工况下的横向振动主要由模态共振导致，为了在不对现有结构及尺寸进行较大改动的情况下抑制其横向振动，对空气弹簧等连接弹簧的刚度及阻尼参数进行优化来抑制模态共振是一种可行的方法。

2 参数影响规律分析

弹簧的刚度和阻尼等参数对系统模态频率和模态阻尼比等有直接影响，通过合理的参数选择与设计可以保证电动振动台整体性能。本节分析了电动振动台系统主要连接弹簧的参数对系统固有特性及横向振动的影响，为参数优化提供参考。

对于电动振动台的横向振动而言，影响参数有附加台面支撑空气弹簧的垂向/横向刚度及阻尼、钢片弹簧的垂向/横向刚度、运动系统支撑弹簧处的等效垂向/横向刚度及阻尼，由于运动系统支撑弹簧处的等效垂向/横向刚度及阻尼受到中心导杆接触情况的影响，其实际参数较难按照优化参数获得，故本文主要考虑附加台面支撑空气弹簧的垂向/横向刚度及阻尼以及钢片弹簧的垂向/横向刚度的影响。

2.1 附加台面空气弹簧刚度影响规律

为明确附加台面支撑空气弹簧的垂向/横向刚度ktz/ktx对附加台面加速度输出的影响，在不同参数取值时分别对系统进行扫频，得到系统频响特性受影响较大的频段内随两个参数变化的结果，分别如图4及图5所示。

(a)z向

由图4可知，ktz主要影响z向平移模态频率及阻尼比，模态频率随ktz增加而增加，阻尼比随ktz增加而减小，该参数对绕y轴翻转模态频率及阻尼比有一定影响，因此ktz会影响z向平移模态及绕y轴翻转模态频率处的传递函数幅值，且对二者影响趋势相同；由图5可知，ktx主要影响绕y轴翻转模态及x向平移模态的频率及阻尼比，模态频率随ktx增加而增加，阻尼比随ktx增加而减小，因此ktx会影响绕y轴翻转模态及x向平移模态频率处的传递函数幅值，减小ktx有利于降低横向振动比。

(a)z向

2.2 附加台面空气弹簧阻尼影响规律

对于附加台面支撑空气弹簧的垂向/横向阻尼ctz/ctx，系统频响特性受影响较大的频段内随两个参数变化的结果,分别如图6及图7所示。

(a)z向

由图6可知，ctz主要影响z向平移模态、绕y轴翻转模态及x向平移模态的阻尼比，阻尼比随ctz增加而增加，对模态频率影响较小，因此ctz会影响z向平移模态、绕y轴翻转模态和x向平移模态频率处的传递函数幅值，增加ctz有利于降低横向振动比；由图7可知，ctx主要影响绕y轴翻转模态和x向平移模态的阻尼比，阻尼比随ctx增加而增加，因此ctx会影响绕y轴翻转模态和x向平移模态频率处的传递函数幅值，增加ctx有利于降低横向振动比。

(a)z向

2.3 钢片弹簧刚度影响规律

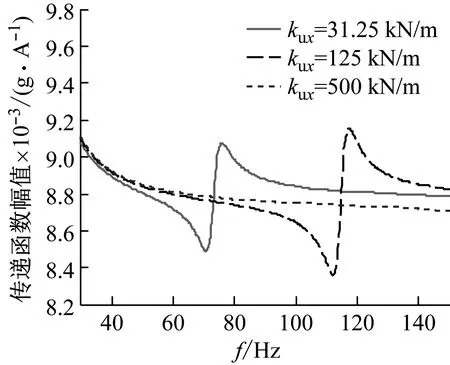
系统频响特性受影响较大的频段内随钢片弹簧的垂向/横向刚度kuz/kux变化的结果,如图8及图9所示。

由图8可知，kuz主要影响z向平移模态及绕y轴翻转模态频率和阻尼比，但对传递函数幅值影响微弱，因此对横向振动比影响也较小；由图9可知，kux主要影响绕y轴翻转模态及x向平移模态的频率及阻尼比，且对x向平移模态影响更为显著，模态频率随kux增加而增加，阻尼比随kux增加而减小，因此kux会影响x向平移模态频率处的传递函数幅值，减小kux有利于降低共振峰值处的横向振动比，而在x向平移模态共振频率接近目标频带上限且刚度参数允许时，通过增加kux来避免在目标频带内发生该阶模态共振可以更好地抑制横向振动比。

(a)z向

3 连接弹簧参数优化设计

3.1 电动振动台横向振动优化评价指标

目前，对于电动振动台的横向振动，标准中多使用定频横向振动比进行评价与测试。但是，为了利用电动振动台进行路面激励工况下车辆关键零部件的可靠性与疲劳测试，主要目标为减小路谱覆盖频段的整体横向振动量级，从而保证测试的准确性。因此，对于这一情景下的横向振动，本文综合考虑横向振动传递函数中的共振峰值及2～120 Hz整体传递函数幅值量级，确定了适用于本问题的优化评价指标，指标δ1表示运动系统沿x轴横向平移及绕y轴翻转的模态共振频率处x向与z向振动传递函数峰值相对比值，表达式如式(3)所示；指标δ2为x向与z向振动传递函数幅值之比在2～120 Hz频率内的积分，用于表征全频段内的横向振动量级，表达式如式(4)所示。

(3)

式中：Hxx及Hxθ分别为沿x轴横向平移及绕y轴翻转的模态共振频率处x向振动传函幅值；Hzx及Hzθ分别为沿x轴横向平移及绕y轴翻转的模态共振频率处z向振动传函幅值。

(4)

式中,Hx(f)及Hz(f)分别为频域x向及z向传函幅值。

3.2 电动振动台连接弹簧参数优化

基于参数影响分析，对电动振动台横向振动比影响较大的参数有ktx、ctx、ctz及kux，针对本文研究的电动振动台系统，上述4个参数为本节选取的优化变量，为了不过于影响原系统的特性，各变量优化范围如表2所示，为初始值的一半到初始值的3倍。参考《弹簧手册》[22]，对于ktx及kux，帘线材料的纵向弹性模量对空气弹簧的径向刚度有显著影响，且对垂向刚度影响较小，而材料杨氏模量与横截面积对钢片弹簧轴向刚度有显著影响，通过改变材料特性及形状尺寸可以得到期望的刚度值；对于ctx及ctz，通过阻尼孔等的设计可以得到期望的空气弹簧轴向及径向阻尼值。

表2 优化变量取值范围

本节采用NSGA(Non-dominated sorting genetic algorithm)-II算法进行参数优化[23]，由于NSGA算法运用了非支配分类程序，可以使多目标简化为单个的适应度函数，故具有较高的优化效率，并可以用于解决任意优化目标数目的参数优化问题。在NSGA算法的基础上，NSGA-II算法进一步通过定义拥挤距离指标来估计某个点附近解的密度，以此来取代适应度共享，具有计算复杂度低及效率高的优势，算法的鲁棒性较好[24]，其流程框图如图10所示。