超声电机摩擦材料局部剥落故障特征提取方法

安国庆，张群虎，安 琪，韩晓慧，李 争，薛智宏

(河北科技大学 电气工程学院，石家庄 050018)

行波型超声电机具有保持转矩大、无电磁干扰、响应快的特点，被广泛应用于航空航天、医疗器械、光学仪器、智能机器人和军事装备等领域[1-2]。该电机利用压电材料的逆压电效应，在弹性体表面激发共振，通过定转子之间的摩擦作用驱动旋转。然而，摩擦材料材质配比、粘结层胶质含水量和均匀度、粘结层气泡混入等因素常会导致摩擦材料局部剥落现象。摩擦材料的剥落边缘与定子金属弹性体的持续高强度摩擦，将加速缺损面积的扩增。由于摩擦材料缺损形成的转子接触表面金属材料外露，改变了定转子接触面摩擦状态，摩擦力的不稳定性进而加剧电机转速的波动性[3]。此外，摩擦材料扩增过程中，电机机械谐振频率的偏移将导致定子振动幅值的衰减，进而引发超声电机输出空载转速和最大转矩性能指标的下降，并加速电机性能退化乃至失效[4]。

以TRUM-60-P型号超声电机为例，其空载转速及最大转矩性能指标随摩擦材料缺损宽度的变化情况如图1和图2所示。现有必要研究一种“非侵入式”的摩擦材料故障特征提取方法，实时对其退化状态进行监测，防患于未然。

图1 摩擦材料不同缺损宽度下的空载转速

图2 摩擦材料不同缺损宽度下的最大扭矩

电机定子预留的“孤极”区域可利用正压电效应产生孤极电压信号，常作为反馈用于监测电机的振动情况[5]。摩擦材料故障对电机振动产生的影响，也将引起孤极电压信号的变化。基于以上分析，本文将孤极电压作为信号分析对象，从中提取能够表征摩擦材料剥落程度的故障特征。超声电机作为特种电机，其运行环境存在的振动背景噪声，以及变频驱动器的谐波噪声常间接耦合至孤极电压信号[6]。尤其在摩擦材料故障初期，故障特征提取较困难，为此有必要对孤极电压信号进行降噪预处理。

行波型超声电机最早由Sashida于1983年提出，赵淳生等[7]完成国内首台该类电机研制。由于该类电机发展时间不长，国内外基于孤极电压信号的摩擦材料故障特征提取方法相关文献较少。考虑到孤极电压信号与压电式加速度传感器监测的振动信号产生机理的一致性，基于振动信号分析的旋转机械故障诊断方法对本研究具有较大的参考意义。现行主流方法包括小波分析法、EMD(empircal mode decomposition)法、LMD(local mean decomposition)法等。然而，小波分析法存在基函数和阈值选取困难的问题，EMD法存在模态混叠的问题，LMD法在降噪的过程中存在信号突变和端点效应问题[8-10]。文献[11]提出了局部特征尺度分解(local characteristic-scale decomposition, LCD)算法，并详细阐述了该方法在解决端点效性和缩短分解时间等方面的优势；文献[12-13]分别将LCD法成功应用在滚动轴承故障诊断的降噪预处理和液压泵性能的退化状态识别；文献[14]证明LCD法能有效实现齿轮箱混合故障盲源分离；文献[15]将LCD法成功应用在转子碰摩故障特征提取。为提高损伤检测的灵敏度和可靠性，近年来Teager能量算子受到了国内外学者广泛关注。文献[16-17]利用Teager能量算子对微弱故障信息的放大作用提高了对轴承退化状态识别的灵敏度；文献[18]将Teager能量算子和小波变换相结合提高了层压复合材料损伤监测的可靠性。对于超声电机而言，随摩擦材料局部剥落程度加剧，定子振动存在削波效应，其故障特征分量所处频率及其幅值都会发生变化[19]。而Teager能量算子在跟踪非线性故障信息方面表现出较大优势[20]。

基于以上分析，本文拟借鉴LCD分解与Teager能量算子在旋转机械故障信息提取方面的优势，在超声电机摩擦材料故障诊断这一新的应用领域进行有益尝试。首先通过LCD和相关分析的方法实现孤极电压信号的降噪预处理，其次通过Teager能量算子跟踪故障分量频率与幅值信息，最后提出摩擦材料局部剥落故障特征的计算方法。

1 基于LCD和自相关分析的孤极电压信号重构

1.1 孤极电压信号的LCD预处理

由于超声电机负载、转速、预压力等因素也会影响孤极电压信号的幅值，为此首先对信号进行归一化预处理。设孤极电压信号原始序列为x(t)(t=1,2,…,N)，则归一化处理后的孤极电压信号表示为

(1)

利用LCD方法将归一化的孤极电压信号分解成任意两个相互独立的内禀尺度分量(intrinsic scale component，ISC)，具体步骤如下。

步骤1确定xN(t)时间序列的极值点Mj(j=1,2,…,S)，并记每个极值点对应的时间为tj(j=1,2,…,S)。取任意两个相邻的极大(小)值点(tj,Mj)和(tj+2,Mj+2)构建极值关于时间的函数

(2)

并计算

(3)

由于lj的值仅有2～(M-1)个，需要对两个端点的值l1和ls进行估计。对时间序列延拓，得到两端的极值点(t0,M0)和(tS+1,MS+1)，再根据式(3)计算l1和ls的值，采用3次样条函数拟合所有lj(j=1,2,…,S)，即可得到均值曲线Bl1(t)。

步骤2从原信号中将均值曲线分离，即

h1(t)=xN(t)-Bl1(t)

(4)

h1(t)作为原始序列，重复上述步骤，直到h1j(t)为一个ISC分量，并记CIS,1=h1j(t)。

步骤3将CIS,1从原始数据中分离，即

μ1(t)=xN(t)-CIS,1

(5)

式中，μ1(t)为剩余信号。

步骤4将μ1(t)看作原始信号，重复步骤2～步骤5n-1次，直到剩余信号为一单调信号或小于阈值的常数，则各分量与原始信号之间满足

(6)

LCD对信号的分解可呈现信号能量在不同尺度上的分布，分解出的各层信号中仍含有噪声成分，因此需对分解得到的各层信号进一步区分和重构。

1.2 基于自相关分析的ISC重构

设对归一化的孤极电压信号进行LCD处理后得到了k个ISC分量，现对每个分量进行自相关分析，所得自相关系数序列可表示为[21]

(7)

式中,τ为时移。

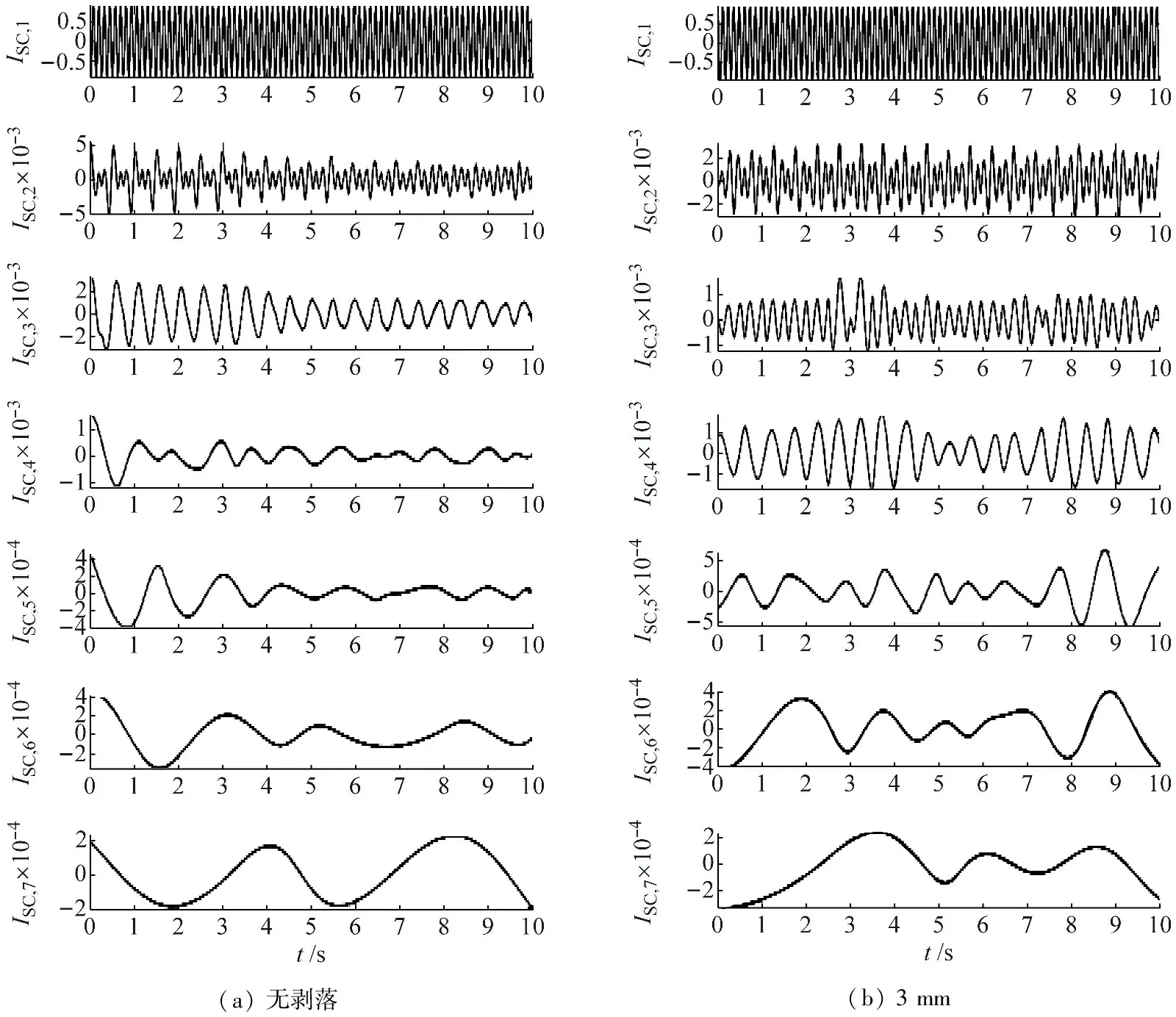
若某ISC分量自相关系数序列中，Rk(τ>0)明显小于Rk(0)，则认定该分量以噪声为主，否则可作为有用故障信息分量给予保留。本文首先令某ISC分量的自相关系数序列中Rmax_a=Rk(0)，若Rmax_a=0则将该分量直接剔除，若Rmax_a≠0则搜索下一个相邻极大值点并记为Rmax_b；其次，将Rmax_a/2作为阈值对Rmax_b进行比较，若Rmax_b

2 基于Teager能量算子的故障特征提取

Teager能量算子可跟踪信号中故障信息的幅值和频率的变化，有利于在频谱分析中凸显故障频率分量。对于重构后的连续信号g(t)，其Teager能量算子定义如下[22]

(8)

文献[23]证明经Teager能量算子处理后的结果与瞬时能量仅相差一个常数，但对振幅和瞬时频率呈平方变化的放大，有利于对摩擦材料剥落导致的相对较弱故障信息进行跟踪分析。随着行波型超声电机摩擦材料局部剥落面积扩增，一方面其旋转速度将会逐渐下降，孤极电压信号包络的“削波”现象将愈发明显；另一方面，受摩擦材料剥落影响而引发的低频段故障信息分量幅值将增大。基于以上分析，首先将Teager能量算子处理后的信号ψ[g(t)]转换至频域；其次在低频段进行搜索，并锁定该范围内最大幅值分量，记其幅值为Afault，对应频率为Ffault；最后，将故障特征定义为

(9)

由式(9)可知，特征值将与故障分量频率成反比，与其幅值成正比。

3 试验分析

3.1 试验数据采集

为检验本文所提故障特征提取方法的有效性，摩擦材料局部剥落故障下的孤极电压信号样本由行波型超声电机试验平台采集完成，如图3所示。

图3 行波型超声电机试验平台

被测行波型超声电机型号为TRUM-60-P，堵转转矩为 0.6 N·m, 空载转速为 100 r/min。驱动器驱动频率为40.8 kHz，与其同频的孤极电压信号由TiePieengineering公司的HandyscopeHS4型数据采集卡采样保存。采集卡采样频率设为500 kHz，每组样本采样时间为0.5 s。以3 mm为单位间隔，通过人为设置不同摩擦材料局部剥落宽度(0～30 mm)，共在预置的11种退化状态下进行了孤极电压信号样本采集(当摩擦材料剥落宽度为30 mm时，电机无法连续平稳旋转，处于失效状态)。受篇幅限制，其中0，3 mm，18 mm，30 mm剥落状态的摩擦材料样本情况，如图4所示。

不同剥落状态对应空载转速变化情况见图1。图1中当剥落宽度≤6 mm时，空载转速指标退化速降在10%以内，不易察觉。因此，若提取的故障特征既能定量反映缺损宽度，又能敏锐表征摩擦材料小面积脱落情况对早期故障进行预警，将有较大的工程应用意义。

以图4中样本为例，采样的孤极电压时域信号如图5所示。

图4 摩擦层剥落故障样本

由图5可知，不同摩擦材料剥落宽度下孤极电压时域信号波形发生了明显变化，即故障对电机定子整体振动情况产生了直接影响。相同采样时间对应的不同样本，波形包络“削波”现象明显，即可从频谱分析中进一步提取表征退化程度的故障特征。

3.2 基于LCD-Teager的故障特征提取

以图5中的孤极电压信号样本为例，对归一化后的信号进行LCD预处理，分别共得到7个ISC分量，如图6所示。

图5 摩擦材料局部剥落故障下孤极电压时域信号

图6 孤极电压信号ISC分量

将各ISC分量进行自相关运算，自相关系数序列中统计的极点信息,如表1所示。

表1 ISC分量自相关系数序列中统计的极点信息

根据1.2节所述ISC分量重构原则，表中CIS,1～CIS,3分量满足Rmax_b>Rmax_a/2的要求，归为“重构分量”，而CIS,4～CIS,7分量由于Rmax_b

将图7中的重构信号进行频谱分析，结果如图8所示。

图7 LCD-Teager预处理后的孤极电压时域信号

图8 LCD-Teager预处理后的孤极电压频谱

本文对试验过程中采集的11组不同局部剥落宽度的孤极电压信号分别进行LCD-Teager信号预处理。预处理后信号频谱中故障分量的信息统计,如表2所示。表2中根据式(9)计算得到了不同剥落宽度下的故障特征值。

由表2可知，随摩擦材料缺损宽度增加，频谱故障信息分量幅值逐渐增大，分量对应的频谱位置逐渐减小左移。故障特征值随摩擦材料局部剥落宽度的变化趋势,分别如图9所示。

表2 LCD-Teager预处理后信号的故障分量信息统计

由图9可知，基于LCD-Teager的故障特征从正常到失效的过程中故障特征近似呈线性趋势递增，且在剥落初期(根据图1中缺损宽度小于等于6 mm，空载转速指标退化速降在10%以内作为参考)表现出了良好的故障表征能力。

为对比LCD-Teager方法在故障特征提取过程中所起的作用，原始采样数据对应的故障特征计算结果,如图10所示。

由图9和图10对比可知，原始信号的计算结果虽整体呈上升趋势，但波动较剧烈，且在摩擦材料剥落宽度18 mm以内无法表征剥落实际程度。

图9 基于LCD-Teager的故障特征变化趋势

图10 未经预处理的原始信号故障特征

3.3 故障特征抗噪性能分析

为验证故障特征在噪声环境下的适用性，在原始孤极电压信号样本的基础上仿真叠加了信噪比等级为0的高斯白噪声信号，并与其他现行主流去噪方法的计算结果进行了对比，结果如图11所示。图11中用于对比的方法包括小波分解、EMD分解、LMD分解3类，并参照分解后所得分量的自相关分析重构原则，经Teager能量算子处理后，由式(9)计算出对应的故障特征值。

由图11中各方法对比可知，在噪声背景下，Wavelet-Teager方法对应的故障特征，当剥落宽度大于12 mm时波动较大；EMD-Teager方法对应的故障特征在摩擦材料局部面积剥落扩增过程中，整体都呈现较为剧烈的波动趋势；LMD-Teager在摩擦材料故障初期波动明显，当剥落宽度大于15 mm时呈现了良好的上升趋势。本文所提出的基于LCD-Teager的故障特征，较图7中的计算结果而言，由于受到噪声干扰，出现了数值整体向下偏置的情况。然而，其在变化趋势上仍具备近似线性的故障表征能力，较其他传统方法表现出更好的背景噪声适用性。

4 结 论

(1)行波型超声电机摩擦材料出现局部剥落故障后会导致定子振动发生变化，孤极电压信号低频段频谱成分的变化可有效反映故障信息。

(2)ISC的自相关分析重构的方法可有效滤除背景噪声，Teager能量算子具备放大行波型超声电机摩擦材料局部剥落故障信息的能力，所提出的基于LCD-Teager的故障特征提取方法可有效表征摩擦材料局部剥落的扩增趋势，对早期故障有效，且具备一定背景噪声适用性。

(3)本文所提出的方法适用于行波型超声电机恒转矩负载运行情况，然而对于电机非平稳运行下故障特征的优化仍具有较大研究空间。围绕该故障特征的相关工作，未来还可向摩擦材料退化状态识别以有效剩余寿命预测方向进一步拓展。