基于VMD和DBN的非线性结构模型参数识别

2022-05-16王佐才丁雅杰袁子青

振动与冲击 2022年9期

莫叶，王佐才,2，丁雅杰，袁子青

(1.合肥工业大学土木与水利工程学院，合肥 230009；2.安徽省土木工程防灾减灾工程技术研究中心，合肥 230009)

随着工程辅助计算技术和理论的发展，结构模型修正的研究取得了许多重要进展[1-5]。然而，非线性普遍存在于在役的工程结构中，例如，材料的非线性、几何的非线性以及环境对结构的非线性影响等。此时，结构通常表现出复杂的非线性动力学行为。采用线性模型模拟，难以获得正确的结果。因此，有必要开发一种高精度的非线性结构模型修正方法。研究结构的非线性模型修正，不仅对工程结构的安全运营监测与评估领域有重要的意义，也推动着结构模型修正理论的进一步发展。

非线性结构模型参数识别可归结为一个非线性优化问题，它通常面临求解过程复杂、容易陷入局部最优解等困难。而神经网络通过学习结构振动响应特征量与非线性模型参数之间的关系，可直接估计出非线性模型参数。这使得神经网络在非线性结构模型参数识别的领域逐渐显示出广泛的应用潜力。例如，Xie[12]等开发了一种基于神经网络的Bouc-Wen滞回系统的识别方法。Hasancebi等[13]利用一个3层的神经网络对T型梁桥的有限元模型进行修正，识别出相应的线性和非线性模型参数。由于这些神经网络简单的结构和较低的学习效率，使得它们并未广泛应用于非线性模型参数识别的领域。

针对非线性结构模型参数识别中寻优过程复杂的问题，本文提出了一种基于基于变分模态分解(variational mode decomposition, VMD)和深度置信网络(deep belief network, DBN)的非线性结构模型参数识别方法。与现有的方法不同，本文方法将非线性结构模型参数识别转化为正问题进行求解。利用Dragomiretskiy等[14]提出的VMD这一自适应信号分解算法与希尔伯特变换(Hilbert transform, HT)提取非线性结构振动响应主分量的瞬时参数。并将DBN这一深度神经网络引入非线性结构模型参数识别中，利用其泛化能力拟合非线性模型参数与主成分分析后的瞬时参数之间的复杂映射关系。避免了求解复杂的非线性逆问题，提高了非线性模型参数识别的计算效率和精度，具有良好的抗噪性。通过地震荷载激励下的两个不同非线性类型的双自由度模型和一个复杂非线性框架的数值算例，验证了本文方法的有效性和抗噪性。最后，通过一个简谐激励下的高压输电结构振动台试验进一步验证了该方法的有效性。数值和试验结果表明，该方法能够较高精度地识别非线性结构模型参数，且具有良好的噪声鲁棒性与较高的计算效率。

1 非线性结构的瞬时参数识别

1.1 VMD原理

VMD算法是一种自适应的非递归模态分解法。该算法利用交替方向乘子法算法依次迭代求得约束变分模型的最优解，从而获得K个中心频率为ωk的本征模函数(intrinsic mode function，IMF)。VMD的分解过程可总结为：

(1)

(2)

(3)

步骤4给定ε>0，当满足式(4)时，则停止迭代。否则，重复步骤2～步骤4。

(4)

由上述过程可知，VMD算法中要预先确定参数K和α。当α取默认值2 000时，一般满足大多数工程需求。参数K的选取已有多种方法，本文根据信号的傅里叶谱进行选取[15]。

1.2 基于VMD的非线性结构瞬时参数识别

对于一个n自由度非线性结构，其受迫振动的微分方程可以写为

(5)

式中，M(t),C(t),K(t)分别为时变质量阵、阻尼阵和刚度阵。

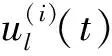
(6)

对VMD分解出的IMF进行HT，其解析信号可表示为

Zi(t)=ui(t)+jH[ui(t)]=Ai(t)ejφi(t)

(7)

(8)

φi(t)=arctan(H[ui(t)]/ui(t))

(9)

从而定义瞬时频率为

(10)

强荷载作用下，HT确定的非线性结构瞬时频率包括一个慢变频率分量和一个快变频率分量。构造合适的低通滤波器可得到瞬时频率的慢变成分fsl(t)。其中，fsl(t)近似为结构的固有频率[16]。由于Ai(t)和fsl(t)分别反映了非线性结构振动响应随时间变化的幅值和相位信息，可用于非线性结构模型参数的识别。

2 基于VMD和DBN的非线性结构模型参数识别

2.1 DBN原理

DBN是一种概率生成模型，通过将数据从输入映射到输出，它可以表示任意形状的函数。

2.1.1 限制玻尔兹曼机模型

限制玻尔兹曼机(restricted Boltzmann machines, RBM)是一种广义随机神经网络，它为内部分布未知的数据提供学习模型。RBM由两层神经元组成:一层为可视层由可视元组成，用于训练样本的输入；另一层为隐藏层由隐藏元组成，作为特征检测器[17]。RBM模型的基本结构,如图1所示。

定义可视层向量v={v1,v2,v3,…,vm}∈(0,1)；隐藏层向量h={h1,h2,…,hn}∈(0,1)；权重矩阵w；可视元的阈值a，隐藏元的阈值b。RBM是基于能量的模型，因此所有可视元和隐藏元的联合状态能量函数E(v,h)可表示为

(11)

式中：m为可视元数；n为隐藏元数。v与h之间的联合概率分布可描述为

(12)

(13)

当可视层向量v的状态已知，则隐藏层h的第j个单元的条件概率可表示为

(14)

同理，可视层向量v的第i个单元的条件概率为

(15)

式中：sig(x)=1/(1+e-x)为激活函数。

假定参数ψ={ai,bj,wij}，ψ为第i个可视元的状态。RBM的训练是一种无监督的学习过程，其目的是求得参数ψ，以拟合训练数据中输入与期望输出之间的关系。可通过最大化样本的对数函数获得参数ai,bj和wij的最优解

(16)

式中，L为训练样本的总数，l∈(0,L)。本文采用对比度散度快速学习算法求解上述优化问题，获得参数ψ的最优解。

2.1.2 DBN的结构与训练

完整的DBN结构是通过RBM的堆叠以及在其顶部添加BP(back propagation)神经网络所组成的，每层的神经元数由实际问题决定。

DBN的训练可概括为两个步骤：无监督的预训练和有监督的微调。首先，RBM网络的每一层都经过独立、无监督的训练，以确保尽可能多地保留训练数据的特征信息。无监督训练完成后，将在DBN的顶层建立BP神经网络，利用BP算法进一步优化之前的初始权重。DBN的训练过程如图2所示。

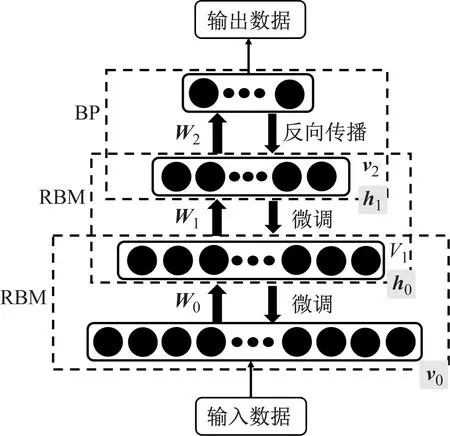
图2 DBN的训练过程

2.2 基于VMD-DBN的非线性结构模型参数识别的步骤

利用DBN描述非线性模型参数θ={θ1,θ2,…,θi}与振动响应的瞬时参数y={A(t),fsl(t)}之间的关系

θ=f(y)

(17)

通过训练，DBN可求得非线性映射函数f。将实测振动响应的瞬时参数输入训练好的DBN中，可识别出修正后的非线性模型参数。

基于VMD-DBN的非线性结构模型参数识别方法可分以下5个步骤。

步骤1非线性结构振动响应特征量的选取：将VMD和HT提取振动响应主分量的A(t)和fsl(t)为振动响应的特征量；

步骤2待识别参数的选取：选择非线性模型常参数作为待识别参数；

步骤3样本数据的生成：需要选取具有代表性的待识别参数样本点。故本文采用均匀设计法生成一定数量的待识别参数组，计算对应的振动响应，再利用VMD和HT提取振动响应的特征量；

步骤4DBN的训练：为加快DBN的收敛速度，对提取的瞬时参数进行主成分分析后再输入DBN，将待修正参数作为期望输出，对DBN进行训练；

步骤5非线性模型参数的识别：将主成分分析后的实测振动响应的瞬时参数输入训练好的DBN，其输出即为修正后的非线性模型参数。

2.3 非线性模型参数识别的精度评价指标

将识别出的非线性模型参数带入非线性模型中，通过定义Eacc,Ef,Eamp这3个指标来评价本文方法的识别精度。其中，Eacc,Ef,Eamp分别为实际结构与修正后模型之间的加速度相对误差、瞬时频率慢变成分相对误差与瞬时幅值相对误差，可写为

(18)

(19)

(20)

式中:下标u和t分别为修正后的非线性模型与实际结构。

3 数值算例

3.1 双线性节点模型的参数识别

本算例对2维双自由度非线性结构进行分析，如图3所示。用elastic Beam-Column element定义柱单元，底部的非线性节点模型用于模拟结构的非线性行为。通过使用带有两个双线性钢材料模型的弹簧单元模拟非线性节点模型。双线性钢材料模型的滞回特性由F,E,b这3个参数决定，分别代表初始屈服强度、杨氏模量和刚度比。这两个双线性材料模型分别在弹簧元件的剪切和扭转方向上定义。非线性模型参数的理论值分别设置为：Fs0=20 kPa,Es0=2.5 MPa,bs0=0.3,Ft0=2.0 kPa,Et0=2.0 MPa,bt0=0.5。基底激励采用Northridge地震波，如图4所示。利用OpenSees[18]计算顶层的加速度，假定为实测响应，如图5所示。为模拟实际测量中噪声的影响，向实测响应中加入5%的高斯白噪声。其中:Pnoise=5%×Psignal;Pnoise为高斯白噪声的功率；Psignal为无噪声情况下的模拟加速度响应的功率；5%即为噪声与加速度响应信号的功率比。

图3 二层非线性节点模型

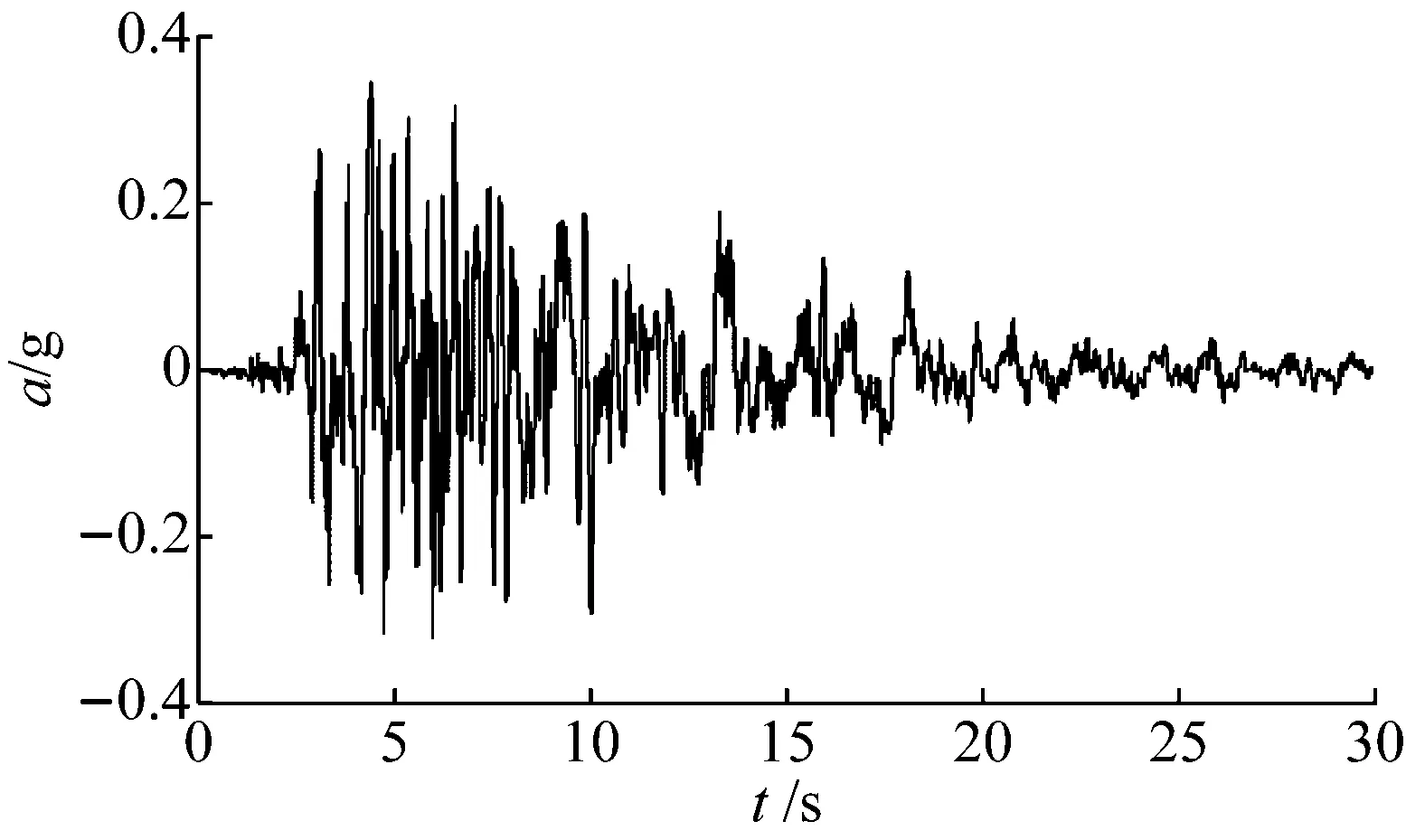
图4 Northridge地震波

图5 顶层加速度

与加速度相比，提取的瞬时幅值和瞬时频率随时间缓慢变化。因此，不需要选择所有被测点。本算例分别选取加速度响应瞬时幅值和瞬时频率的慢变成分的30个局部峰值点作为提取的瞬时特征参数。利用VMD和HT提取出顶层加速度响应主分量的瞬时幅值A(t)和瞬时频率的慢变成分fsl(t)，如图6所示。

(a)瞬时幅值

为避免参数不同量级可能导致的数值困难，将待识别参数定义为非线性模型参数的无量纲比例因子。即，θ1=Fs/Fs0,θ2=Es/Es0,θ3=bs/bs0,θ4=Ft/Ft0,θ5=Et/Et0,θ6=bt/bt0。使每个参数在原参数±20%内波动，即这6个比例因子的上下界分别定义为：[0.8,0.8,0.8,0.8,0.8,0.8]和[1.2,1.2,1.2,1.2,1.2,1.2]。采用均匀设计法生成80组待修正参数的样本点，利用VMD和HT提取相应的顶层加速度的瞬时特征参数。为简化DBN的结构，加快其收敛速度，预先对输入的A(t)和fsl(t)进行主成分分析。然后，将生成的训练数据输入DBN，进行训练。最后，将主成分分析后的实测响应瞬时参数输入训练好的DBN中，直接估计待识别模型参数。本算例中，采用具有两层RBM的DBN结构。其中，RBM的神经元数分别取10和12；顶层BP网络的神经元数目取6；学习率为0.01，期望误差为0.000 1。

经计算，待识别参数的修正结果为：θu1=1.01,θu2=1.06,θu3=1.00,θu4=0.994,θu5=0.995和θu6=1.01。误差指标分别为：Eacc=0.61%,Eamp=0.40%与Ef=0.004%。将待识别参数的修正结果带入非线性模型，计算顶层加速度响应与其主分量的瞬时参数，并与实测结果进行对比，如图7所示。表明本文所提出的非线性结构模型参数识别方法不仅精度高，修正后的模型还可以反映实际结构的非线性动力特征。

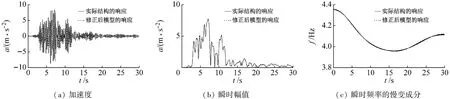
图7 修正后的非线性模型与实际结构的振动响应对比

3.2 Bouc-Wen模型的滞回参数识别

为研究本文所提出的方法对不同非线性类型模型的适用性，建立结构形式与3.1节算例类似的模型，改用Bouc-Wen材料本构模型来定义底层柱的材料。通过合理地选择Bouc-Wen模型的滞回参数，可以模拟结构在地震荷载作用下的非线性动力响应。本节对Bouc-Wen模型的6个滞回参数：α,β,γ,δv,δη和n进行识别。其中：α为线性与非线性刚度之比；β，γ为滞回环形状的基本控制参数；n为屈服的尖锐程度参数；δv为强度退化因子；δη为刚度退化因子。其初始值分别设置为：α0=0.3,β0=200,γ0=200,δv0=0.3,δη0=1.50,n0=1.5。为研究本文方法在Bouc-Wen模型滞回参数识别中的抗噪性，对模拟的加速度中加入5%高斯白噪声。

参数识别的过程与3.1节类似，经计算，Bouc-Wen模型滞回参数的识别结果为：α=0.296,β=200,γ=195.2,δv=0.156,δη=1.48,n=1.52。误差指标分别为：Eacc=5.3%,Eamp=2.7%与Ef=0.096%。上述结果说明本文提出的方法可以高精度地识别Bouc-Wen模型的滞回参数，且仍具有良好的抗噪性。

为进一步有效证明本文方法在非线性结构模型参数识别方面的优越性，分别对比了基于DBN、VMD和DBN、VMD和BP神经网络这3种算法的识别精度与计算效率，结算结果如表1所示。其中，基于DBN的识别算法直接利用DBN拟合非线性结构模型振动响应与非线性结构模型参数之间的关系。

表1 不同算法的识别误差指标与计算时间对比

由表1可知，本文方法的识别精度高于基于VMD与BP神经网络的识别方法；相较于直接利用DBN进行非线性结构模型参数识别，本文方法在保证较高的识别精度同时，缩短了计算时间，提高了计算效率。因此，本文方法利用VMD与HT提取振动响应主分量的瞬时参数作为输入，降低了DBN的输入维度，使计算效率得到较大提升。而且，DBN克服了BP神经网络随机初始化权值矩阵与易陷入局部最优值的缺陷，从而有效保证了识别的精度。

3.3 复杂框架的非线性模型参数识别

对一个二维的3层3跨的钢框架模型SAC-LA3[19]的非线性模型参数进行识别，其结构形式如图8所示。采用基于刚度法的梁柱单元定义所有的梁和柱。使用一个改进的GMP非线性材料本构模型来定义结构的材料，其滞回特性主要由3个参数fy、E和b决定，分别表示初始屈服强度、杨氏模量和刚度比。除了这些参数，还有3个辅助参数R0、cR1和cR2控制从材料从弹性阶段过渡到塑性阶段，本算例中假定这3个辅助参数为已知常数。因此，共有6个参数：fBeam，y，EBeam，bBeam，fCol,y，ECol，bCol作为该有限元模型的未知非线性模型参数。其中，fBeam,y，EBeam，bBeam是钢梁的材料参数，fCol,y，ECol，bCol定义了钢柱的非线性行为。这6个滞回模型参数的理论值分别设置为：fBeam,y=345 MPa，EBeam=200 GPa，bBeam=0.16，fCol,y=250 MPa，ECol=200 GPa，bCol=0.08。选用与3.1节算例相同的外部激励。3个加速度计S1,S2和S3，用来记录框架模型在地震激励下的加速度响应(见图8)。其中，S3记录的顶层加速度响应作为实测的响应,用于非线性结构模型参数识别。

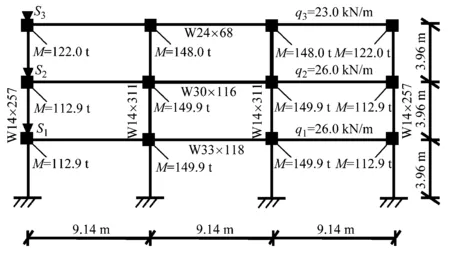
图8 3层3跨非线性框架模型

定义待识别参数为：θ1=fBeam,y/fBeam,y0,θ2=EBeam/EBeam,0,θ3=bBeam/bBeam,0,θ4=fCol,y/fCol,y0,θ5=ECol/ECol,0,θ6=bCol/bCol,0。非线性模型参数分别在原参数的±25%内波动，故待识别参数θi(i=1,2,…,6)的上下界定义为：[0.75,0.75,0.75,0.75,0.75,0.75,0.75]和[1.25,1.25,1.25,1.25,1.25,1.25,1.25]。利用均匀设计法生成60组待修正参数的样本点，按照2.2节中的步骤识别该框架模型的非线性参数。为进一步研究本文方法的抗噪性能，在实测的加速度响应中加入5%高斯白噪声。经计算，待识别参数的修正结果为：θu,1=1.02,θu,2=1.00,θu,3=1.00,θu,4=1.03,θu,5=0.988和θu,6=0.992。识别误差指标为：Eacc=2.9%,Eamp=2.0%与Ef=0.05%。

对比5%高斯白噪声影响下，修正后的模型与实际结构的顶层加速度响应、及其主分量的瞬时参数，如图9所示。由图9可知，修正后模型的响应与实际结构的响应比较吻合。在5%高斯白噪声的影响下，Eacc、Eamp和Ef均小于3%，说明该方法具有良好的抗噪性，适用于复杂框架模型的非线性参数识别。

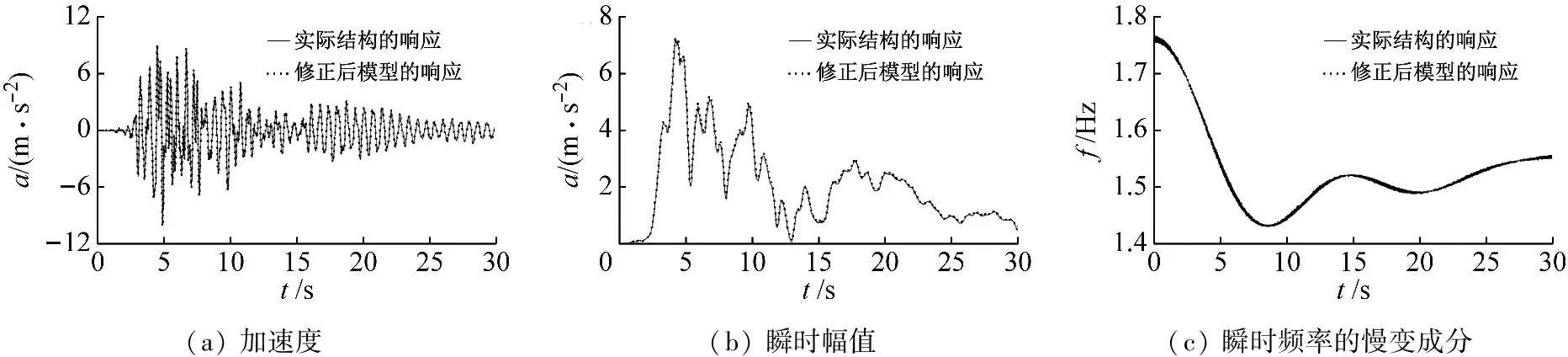
图9 修正后模型与实际结构的响应对比

4 试验验证

为进一步验证论文所提方法的有效性，高压输电结构进行振动台试验，如图10(a)所示。试验装置由3根陶瓷柱和1根工字钢组成，用螺栓固定在振动台上。上部搭建的木桁架用作试验结构的横向支撑。3个加速度计用于记录结构振动响应，如图10(b)所示。其中，振动台底部的加速度计3用于记录输入的外部激励，其加速度记录如图11所示。加速度计2测得的响应用于非线性结构模型参数识别，如图12所示。在试验过程中，当输入的外部荷载超过一定强度时，结构的右侧柱底部支座发生破坏，使结构产生了非线性。详细的试验设置可参考文献[20]。

图11 外部简谐激励

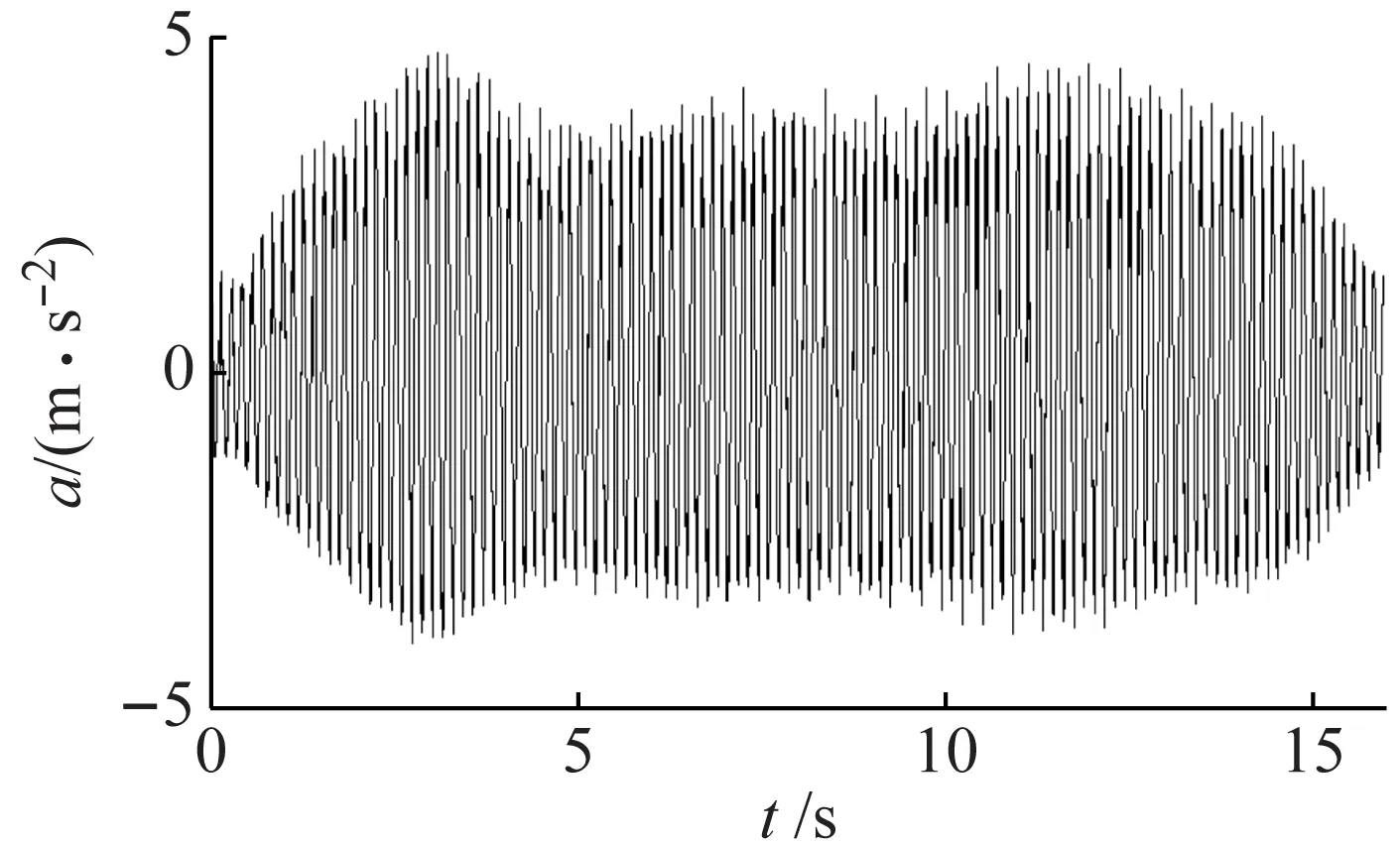
图12 加速度计2测量的加速度响应

试验结构的破坏类型主要为底部支撑的剪切破坏。考虑到右侧支撑的断裂以及其他两个支撑损伤可能导致试验结构的非线性，建立了非线性模型如图13所示。其中，3个底部支撑被定义为与3.1节类似的非线性节点模型。线性弹性梁单元用于模拟3个陶瓷柱和梁，此外，采用4个线性弹簧单元近似模拟上部梁柱的连接特性。

图13 试验结构的非线性模型

由于每个非线性节点模型的非线性特征由6个双线性钢材料模型参数决定，总共选取18个材料参数的比例因子作为待识别参数。基于试验结构与双线性钢材料的特性，定义了3种非线性节点模型的初始值，如表2所示。

表2 非线性结构模型参数的初始值

每个材料参数在原参数±30%内波动。基于均匀设计法生成60组样本，利用本文所提出的方法对非线性模型参数进行识别，识别结果如表3所示。将识别后的参数带入非线性模型，可获得修正后的模型。对比修正后的模型与实际结构的加速度响应及其主分量的瞬时参数,如图14所示。

表3 非线性结构模型参数的识别结果

图14 修正后的非线性模型与实际结构的振动响应对比

由图14可知，基于本文方法修正后的非线性模型响应与实测的响应总体上一致，修正后模型响应的误差在可接受的范围内。经计算，定义的识别误差指标分别为：Eacc=9.6%,Eamp=6.1%与Ef=1.9%。3个误差指标在试验中的应用略大于在数值模拟中的计算结果，基于识别的非线性结构模型计算的振动响应与实测结果基本吻合。