含压电分流阻尼的声学黑洞梁振动特性研究

万志威，朱 翔,3，李天匀,3，李 敬

(1.华中科技大学 船舶与海洋工程学院，武汉 430074；2.船舶与海洋水动力湖北省重点实验室，武汉 430074；3.高新船舶与深海开发装备协同创新中心，上海 200240)

声学黑洞结构具有无附加质量、控制频带宽和可设计性强等特点，在减振降噪方面提供了新的技术。在梁结构中，梁的厚度按照幂函数形式变小，梁中这种楔形结构称作声学黑洞结构[1]。当弯曲波传播到此结构中时，弯曲波的波速会随着板厚度的减小而逐渐减小。在理想的情况下，波速会减小到零，波无法进行传播。在楔形结构敷设阻尼层，可以将传播到楔形结构中心的能量大幅吸收，即弯曲波“陷入”了声学黑洞结构中[2]。Mironov[3]揭示了弯曲波无法在楔形结构中传播的机理。Krylov[4]通过几何声学方法分析了楔形结构局部振动，敷设阻尼层可以有效的降低反射系数[5],声学黑洞在截止频率以上才能实现聚波效应[6]。黄薇等[7]从时域上研究了弯曲波在声学黑洞结构中聚集的现象。Tang等[8]通过半解析法分析了含一维声学黑洞结构的梁振动特性。Deng等[9-10]通过半解析法分析了内嵌多个圆形声学黑洞结构和内嵌环形声学黑洞结构的平板振动特性。半解析法将附加阻尼作为能量的一部分，可以考虑阻尼层与声学黑洞结构的全耦合；且可以通过弹簧来模拟实际上不同的边界条件。

粘贴有阻尼层的声学黑洞结构能有效的聚波和抑振，但由于声学黑洞存在截止频率，在截止频率以下效果不佳[11]。近年来，由压电片外接分流电路组成的分流阻尼，能够通过分流电路产生电磁振荡，与被控结构发生共振，引入局域共振机制，也得到较多关注。

Hagood等[12]分析了通过压电片外接分流电路来耗散机械能。Behrens等[13]通过理论和试验分析了在简支板上连接负电容电路对振动的影响。李宁等[14]通过传递函数法得到了电器元件最优参数表达式。陈良[15]基于长波近似假设将分流阻尼的作用等效为一个附加的具有等效杨氏模量的材料。Wang等[16]在柔性各向同性梁中，采用分流阻尼周期阵列实现可调谐的低频局部共振带隙。压电分流阻尼通过引入局域共振机制，可以通过小尺寸控制大波长弹性波传播，在低频振动控制方面具有显著优势，而这一方面是声学黑洞存在短板[17]。因此，若能将压电分流阻尼与声学黑洞进行结合，发挥两种技术的优势，则能够实现宽频抑振降噪特性。

关于声学黑洞和分流阻尼单独的研究已经很丰富，但将两者结合起来考虑的研究较少。Beck等[18]通过有限元法分析了外接负电容分流阻尼的声学黑洞梁振动特性。Ji等[19]通过有限元法和试验研究了基于复合声学黑洞梁振动的能量收集性能。Zhao等[20]通过有限元法探讨了含有压电片的声学黑洞结构用于能量收集，通过试验[21]研究了含有压电片的声学黑洞在薄板中动态结构剪裁的性能，最后对电路电阻值优化达最大化聚能效果，并进一步通过有限元法和试验研究了含有压电片的声学黑洞结构在振动领域衰减[22-23]。Li等[24]通过有限元法分析了一种宽频有源黑洞装置。以上研究都是基于有限元法以及试验验证，不便于从机理上阐释分流电路参数变化对结构振动的影响。

结合声学黑洞和分流阻尼的优点，本文采用半解析法研究了一种声学黑洞梁和压电分流阻尼的声学黑洞压电复合结构。首先通过半解析法求解了声学黑洞梁的振动特性，并与有限元结果吻合较好，验证了半解析法的有效性。引入分流阻尼，通过等效介质法将分流阻尼等效为具有等效杨氏模量的附加材料，分析了含分流阻尼的声学黑洞梁振动特性，并通过调整电阻电感值对结构第一阶共振峰值进行抑振。分析了电阻电感值对局域共振的影响，从理论上给出了确定局域共振频率近似方法。为声学黑洞结构的低频振动控制提供了新思路。

1 理论部分

1.1 哈密顿原理

一个带有声学黑洞的欧拉梁，如图1所示。梁由厚度按照幂函数变化的声学黑洞部分h(x)=εxm,x∈[x0,xb1]，厚度均匀的主体部分hb,x∈[xb1,xb2]和阻尼层部分hd(x),x∈[xd0,xd1]构成。厚度变化的一端为自由端，厚度均匀的一端由平动弹簧k和旋转弹簧q连接以模拟弹性边界。通过调节k和q的大小可以实现不同的边界条件的模拟。在梁xf处施加一点激励f(t)。

图1 含有声学黑洞的欧拉梁

基于欧拉梁理论，梁的位移场可以表示为

(1)

式中，{u,w}为在梁或者阻尼层上某一点沿x和y方向的位移。将位移函数w(x,t)表示成一系列型函数与广义坐标之积的形式

(2)

通过哈密顿原理，可得到如下的拉格朗日方程[25]

(3)

式中，L为拉格朗日函数

L=Ek-Ep+W

(4)

式中：Ek为系统的动能;Ep为系统的势能;W为外力对系统做功。对于欧拉梁，它们可以表示为

(5)

(6)

W=f(t)·w(xf,t)

(7)

将式(2)和式(4)～式(7)代入式(3)可得方程组的矩阵形式

(8)

式中：M为质量矩阵;K为刚度矩阵;a(t)和f(t)分别是由响应和激励力组成的向量。

a(t)=Aeiωt

(9)

f(t)=Feiωt

(10)

因此，式(8)可以化为

(K-ω2M)A=F

(11)

对于自由振动，向量F为零，因此式(11)可以写为

(K-ω2M)A=0

(12)

由此可以得到系统的固有频率ω和对应的振型A。

1.2 墨西哥帽状小波函数

在半解析模型中，最为关键的是需要寻找一个合适的型函数来表达位移场。尽管在现有对非均匀结构的研究中，多采用幂函数或者多项式作为形函数[26-27]，但是因在厚度减小处型函数会逐渐衰减而对于声学黑洞结构而言难以适用，且存在随位置急剧变化的“奇异”现象。墨西哥帽状小波函数(Mexican hat wavelet，MHW)可以描述几何中的重要信息[28]，适于描述在声学黑洞尖端急剧变化的波群。

因此，本文选取MHW作为型函数，它的表达式为

(13)

通过对自变量进行缩放和平移，可以将式(13)定义的函数扩展为一系列MHW的子函数

(14)

1.2.1 确定缩放因子

当梁的范围为[0,1]时，要使小波函数有效宽度恰好能覆盖梁的整个长度，则有：2×5/2j=1，即2j=10。为了构建一系列的小波函数，必须保证每个小波的有效半径都要落到梁的范围内。可以取更大的j，于是有

j≥ceil(log210)=4

(15)

式中，ceil(x)为最小的整数，ceil(x)≥x。

1.2.2 确定平移因子

要让有效宽度[-5/2j+k/2j,5/2j+k/2j]至少有部分落在[0,1]内。同时为了避免矩阵的奇异性，可以将k的范围[29]取为

(16)

式中，floor(x)为最大的整数，floor(x)≤x。

例如，当x0=1 cm，xb2=10 cm时，将梁的长度进行单位化后，取j=4，则k∈[-2,18]，此时MHW的子函数的分布如图2所示。

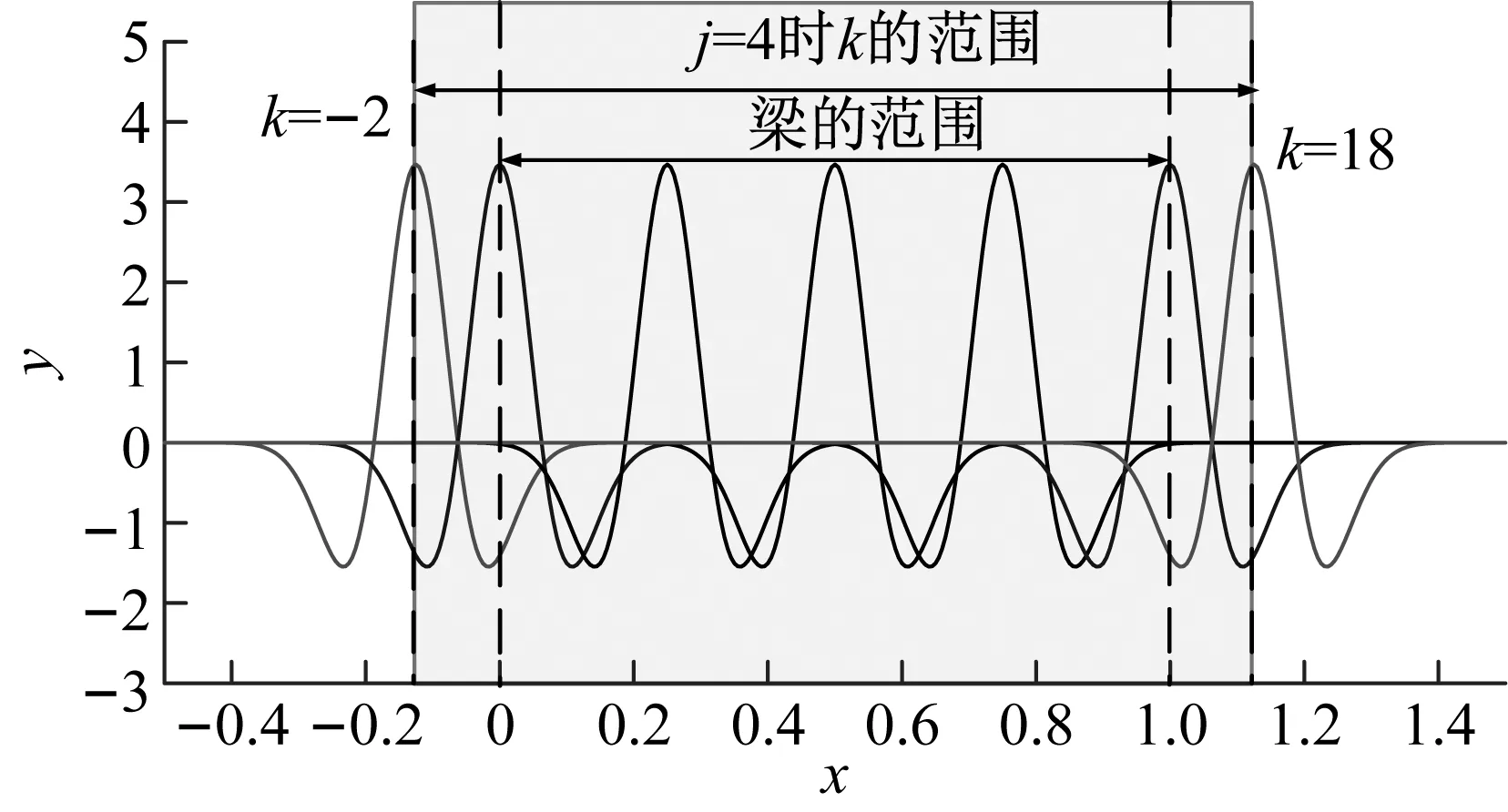
图2 墨西哥帽状小波函数缩放和平移后的分布

2 模型验证

考虑含有声学黑洞的欧拉梁(见图1)。对于边界条件，梁一端处于自由状态，另一端处于固支状态，取平动弹簧k值为1×1010N/m，旋转弹簧q的值为1×106N·m/rad。考虑梁的左端x=1 cm处存在加工精度造成的截断。在COMSOL5.4中建立对应的有限元模型，并进行模态分析。梁的尺寸参数和材料属性如表1所示。

表1 梁的尺寸参数和材料属性

采用本文提出的半解析法计算了含有对称声学黑洞的欧拉梁的固有频率，并提取了前5阶振型，将共振频率和对应的振型与有限元方法进行对比，分别如表 2、图 3所示。两种方法前5阶固有频率最大误差不超过1.0%，且前5阶振型图非常吻合。

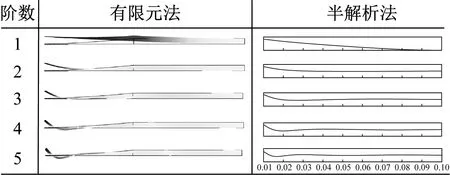
图3 有限元法与半解析法前五阶振型图

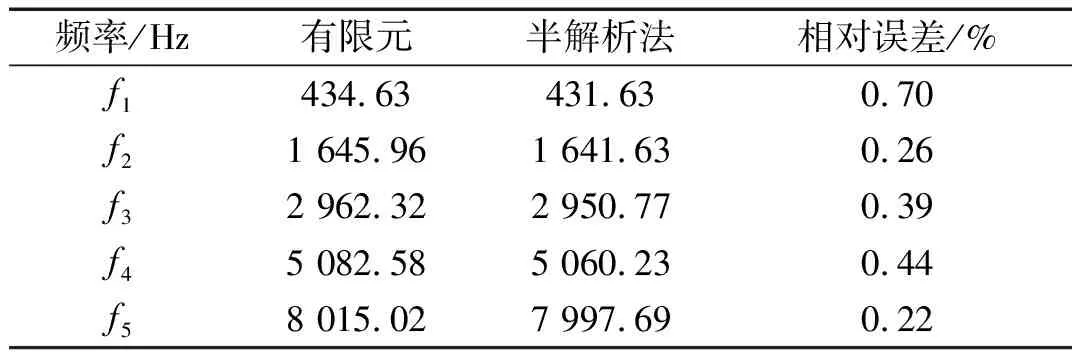
表2 有限元与半解析法共振频率比较

在xf=8 cm处施加F=F0eiωt，幅值F0=1 N的激励力。研究10～5 000 Hz内输出点xout=6 cm处位移幅值随频率变化关系。分别用有限元法和半解析法得到的振动加速度级随频率变化曲线，如图4所示。从图4可知，两条曲线在所计算频率段内十分吻合。因此当选取墨西哥帽状小波作为型函数，设置合适的缩放因子和平移因子时，本文提出的半解析法可有效的模拟梁的横向自由振动和强迫振动，验证了半解析法的有效性。

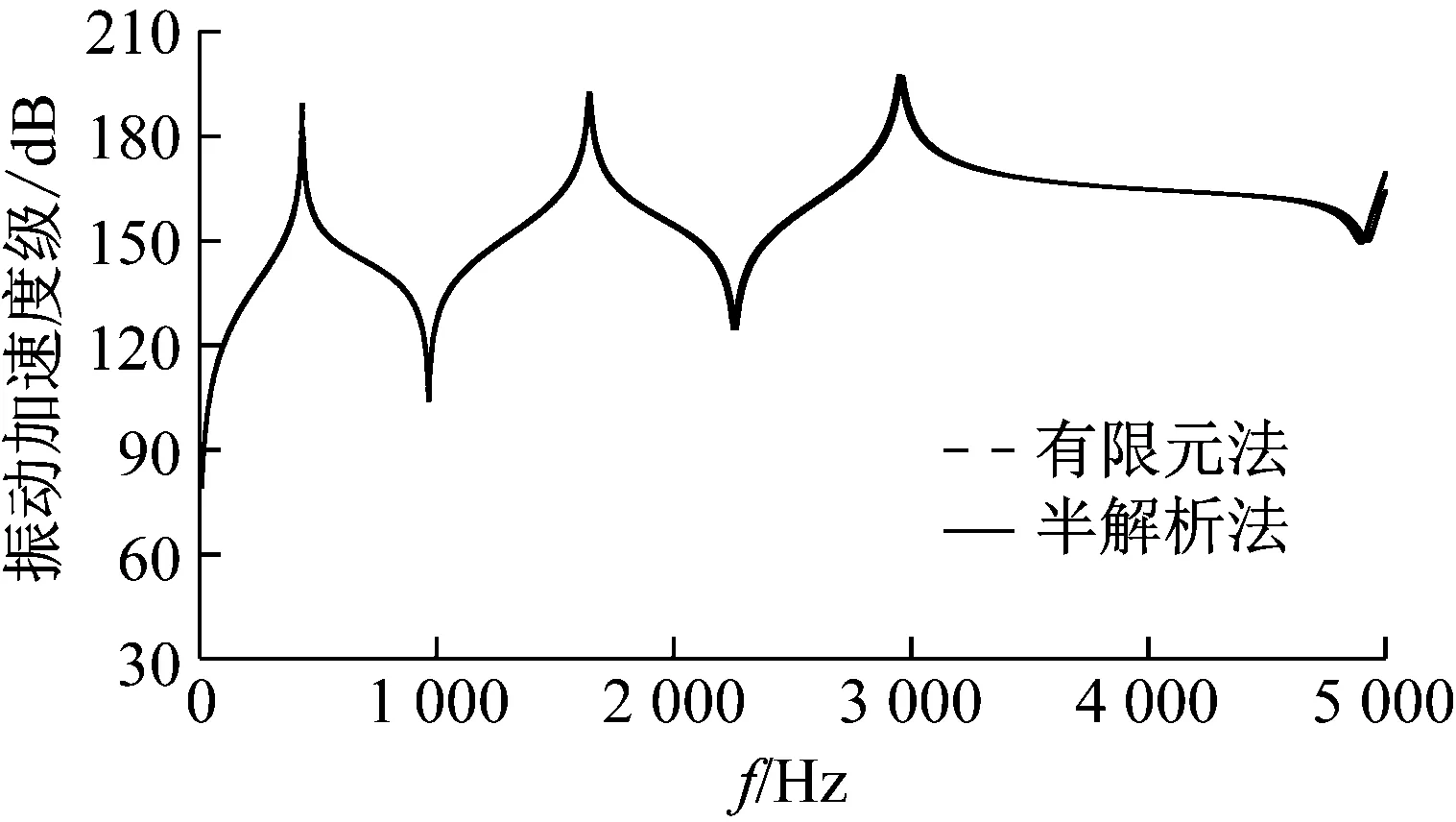
图4 有限元法与半解析法谐响应分析结果

3 含有分流阻尼的声学黑洞梁振动特性分析

含有分流阻尼的声学黑洞梁由基体梁、压电片和分流电路三部分组成，如图5所示。利用等效介质法，将分流阻尼等效为一个均质材料，分析含有分流阻尼的声学黑洞梁振动特性。

图5 含有分流阻尼的声学黑洞梁

3.1 等效介质法

压电晶体在弹性限度范围内，应变和电位移可以由应力和电场两方面产生。因此以应力张量T和电场强度张量E为自变量，应变张量S和电位移张量D为因变量，得到压电方程为[30]

(17)

式中：sE为恒电场弹性柔顺常数矩阵；εT为恒应力介电常数矩阵；dT为压电应变常数矩阵d的转置。

压电片仅受x轴方向的约束，即T1≠0，T2=T3=T4=T5=T6=0。本文所采用的压电片，其极化表面垂直于z轴，即仅考虑z轴方向的电场作用，即E1=E2=0，E3≠0。根据这些条件，压电方程可以化简为

(18)

式中：sE,11为短路弹性柔顺系数;εT,33为恒应力介电常数;d31为压电应变常数。

根据亚波长近似假设，电位移D3在面积为A3的电极上几乎不变，那么电极上的电荷Q可以写为

Q=∬A3D3ds=D3A3

(19)

因此根据基尔霍夫电流定理和戴维南等效电路，分流电路中的电流可以表示成

(20)

式中:s为拉普拉斯常数;hp为压电片厚度;Z为分流电路的复阻抗。

将式(19)和式(20)代入式(18)可得

(21)

式中,Cp为压电片恒应变电容

(22)

从式(21)可知，外接分流电路的压电片在整体结构中表现为一个均质材料[31]，其密度为压电材料密度，杨氏模量为等效杨氏模量Em

(23)

式(23)表明等效弹性模量会随着分流电路的阻抗变化，因此可以通过改变分流电路的阻抗来调整材料属性从而调整局域共振频率。

选取PZT-5H压电陶瓷作为压电片材料，相应的参数值如表3所示。在理论上，压电陶瓷的尺寸大小和位置与普通阻尼材料保持一致。

表3 PZT-5H压电陶瓷参数

3.2 分流电路参数

通过压电材料本构方程和分支电路方程，可以得到系统的广义传递函数，由传递函数表达式可知，对被控结构，由压电元件和分支电路组成的子系统类似于一个调谐质量阻尼器。通过观察包含谐振分流压电材料(resonant shunt piegoelectric，RSP)的系统与包含质量阻尼器(proof mass damper,PMD)的系统之间的相似性，可以解决分支电路参数优化问题。通过类似于PMD分析中传递函数优化方法，可以得到电感L和电阻R最佳值，采用LR串联电路时如图6所示。此时电感电阻的最佳取值为

图6 LR串联电路

(24)

(25)

机电耦合系数K31为反映压电材料的机械能与电能之间相互耦合关系的物理量，对于压电效应，从电边界条件的频率改变得到广义的机电耦合常数[32]。

(26)

式中:ωD,n为分支电路为开路时的模态频率;ωE,n为分支电路为短路时的模态频率。

3.3 数值分析

声学黑洞尺寸与阻尼材料等参数与表1相同。对敷设阻尼层的声学黑洞梁、连接分流阻尼电路(LR串联)的声学黑洞梁和不含阻尼层的声学黑洞梁进行谐响应分析。通过式(24)～式(26)，可算出取第一阶模态频率时，最佳电阻值为794.36 Ω，最佳电感值为4.68 H。在xf=8 cm施加单位激励力，输出点xout=6 cm处振动加速度级随频率变化关系如图7所示。粘贴有阻尼层的模型，因为阻尼材料自身损失因子的作用，降低了共振处的峰值。带有分流电路的模型此时并未表现出优异吸能减振的作用。

(a)

与普通阻尼层相比，分流电路可通过改变杨氏模量来改变等效的刚度。因此下面针对低频处的第一阶共振频率对应的峰值，探讨改变电阻R和电感L的值，使第一阶共振频率处的峰值削减。

3.3.1 分流电路中电感作用

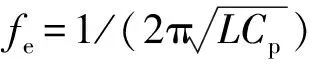
保持电阻值R=50 Ω一定，尝试着调整电感值。电感值减小时，局部共振频率向高频移动。当电感值L=5.35 H时，与电感值L=4.68 H相比，峰值处衰减了4.14 dB，如图8所示。从图8可知，这是因为当局部共振频率与结构共振频率接近时，两个共振峰相互影响，结构振动能量分摊在两个共振峰处，因此结构振动最大响应会下降；仅通过调整电感值使局域共振与结构共振发生耦合可以使振动最大峰值产生衰减。

图8 改变电感值对输出点振动加速度级的影响(R=50 Ω，L=5.29 H，L=5.35 H，L=5.41 H,L=4.68 H)

3.3.2 分流电路中电阻作用

保持电感值L=5.35 H一定，电阻在电路中作为耗能元件，电阻过小会使局域共振处的振动变得剧烈，类似于结构振动的欠阻尼情况，如图9所示。从图9可知，电阻较小，耗能较慢，以致电感和电容之间进行往复的能量交换。增大电阻值会使分流电路局域共振产生的振荡效应消失。为抑制振动峰值为最低水平，电阻取值不宜太大。随着阻尼参数的增大，两个不同的系统模态合并成一个单一的模态，当阻尼参数趋于无穷大时，这两个不同的系统模态会合并成一个单模态，并收敛到具有开路压电元件的系统响应。

图9 改变电阻值对输出点振动加速度级的影响(L=5.35 H，R=10 Ω，R=50 Ω，R=100 Ω，R=1 000 Ω，开路R=∞)

3.3.3 局域共振频率

图10 电阻值为100 Ω电感值为5.35 H时等效杨氏模量实部

3.3.4 分流阻尼结构特性

结合以上关于电阻和电感的讨论，选择电阻值为100 Ω，电感值为5.35 H，将阻抗值优化后的分流电路接入声学黑洞梁。带有分流阻尼电路的声学黑洞梁、粘贴有阻尼层的声学黑洞梁与无阻尼层的声学黑洞梁第一阶共振峰值，如图11所示。普通阻尼层对振动峰值消减作用有限，且无法对指定频率处的振动进行抑制。分流阻尼能通过调整电感值调谐到机械系统的一个模态附近，能连接电阻抑制局部振荡,从而大大提高可达到的模态阻尼比，其效果类似于经典的质量阻尼器或共振减振器。

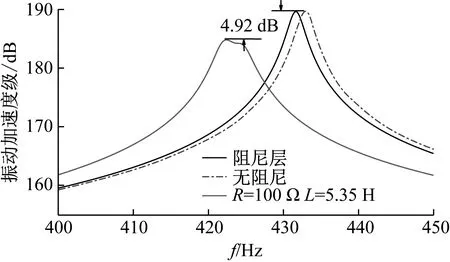
图11 3种模型第一阶共振峰值

质量阻尼器是一个点阻抗，因此只吸收可用的动能。分流压电阻尼在使用中为多端口阻抗，其耗散来自于两个系统节点的相对运动。当基体受到外界激励会产生振动，从而产生形变获得机械能。而压电片由于其正压电效应，受到变形时会在其表面产生电荷，将振动的机械能转换为电能。电能在分流电路中一部分可以被电阻元件转换成热量耗散掉，另一部分由于电感元件和压电片固有电容的相互作用而产生电磁谐振，形成局域振子。因此，分流压电阻尼可以被认为是耗散结构应变能。对于基体结构不同变形处，连接分流阻尼耗散能量的能力也存在差异。这种差异可以反映实际分流阻尼的最佳位置。

在本模型中，通过调整电感电阻值，可以对指定频率处的振动进行衰减，与含阻尼层声学黑洞梁相比，在第一阶振动加速度级峰值可以衰减4.92 dB，具有良好的抑制共振峰的效果。分流阻尼与声学黑洞结合后，在整体结构中表现为粘贴了一层均质材料，其等效杨氏模量既与外接电路的阻抗有关也与频率有关。当调整电感值使杨氏模量在某一频率处发生突变时，结构就会在此频率附近处产生局域共振，当基体结构共振与局域共振发生耦合时，结构振动能量分摊在两个共振峰处，因此结构振动最大响应会下降，而适当的阻值又会有效的抑制振荡，两者结合作用从而可以使结构振动在指定频率处进行有效衰减。

4 结 论

本文通过哈密顿原理，选用墨西哥帽状小波作为型函数，采用能量法对含有声学黑洞的悬臂梁自由振动和受迫振动进行求解，与有限元法结果吻合较好，验证了半解析法的可靠性。将传统阻尼层替换为分流阻尼，通过等效参数法求出了分流阻尼结构的等效弹性模量，讨论了分流电路参数对结构振动特性的影响，得出以下结论：

(1)通过调整电感值使局域共振与结构共振发生耦合使振动响应峰值产生衰减，另一方面适当的阻尼可以使振荡效应消失，电阻值增加到无穷大时结构振动收敛到具有开路压电元件的系统响应。本文通过调整电感电阻值，可以对指定频率处的振动进行衰减，与无阻尼层声学黑洞梁相比，第一阶共振峰处振动加速度级衰减4.92 dB。

(2)可以通过压电片等效弹性模量实部突变对应频率确定局域共振频率。

目前，大量研究表明声学黑洞在截止频率以上能实现聚波能力。本文将声学黑洞和压电分流阻尼结合，改善了声学黑洞在低频振动控制方面的缺陷，为声学黑洞结构的低频振动控制提供了新的思路。后续可以进一步开展不同电路形式的分析以及优化参数实现振动综合控制。