基于随机重构图结构的图神经网络分类算法

刘颖颖,叶海良,杨 冰,曹飞龙

(中国计量大学 理学院,浙江 杭州 310018)

图是基本的数据结构,在实际生活中这些数据来自社交媒体、交通、语言学和化学[1-3]等领域。图神经网络(Graph Neural Networks, GNN)[4]架构广泛应用于节点分类[5-7]、图分类[8-9]、链接预测[10-11]等任务中,它通过对这些图结构数据执行邻居聚合,实现特征提取。

经典的图卷积网络(Graph Convolutional Networks, GCNs)[12]及其变体在消息传递机制中的关键步骤是特征聚合,即节点从拓扑邻居中聚合信息。然而,最近的研究揭示了特征聚合过程中的一些问题。Li等[11]研究发现,图神经网络对在节点特征执行聚合的过程中,破坏了原始特征空间的节点相似性,这意味着节点在其邻居节点中获得信息量受限。为了解决此问题,Wei等人[13]通过实验证明了k-近邻(k-nearest neighbor,kNN)图结构[14]可以作为原始图结构信息的补充,在特征聚合过程中捕获比原始邻接矩阵更多的相似信息。

另外,大多数GCNs的特征传播过程有特定的传播规则,这种确定性传播[12,15]往往使节点对其邻域有很大的依赖性,使节点在更新的过程中很轻易地被数据潜在的噪声所误导。一些研究通过转换节点信息[15-17]或重构图结构[18-19]等方法来解决这一问题。Feng等[15]通过设计的随机传播将局部节点信息传递到其邻域,不足的是该模型随机删除部分节点信息从而损失了完整节点信息。GraphSAGE[16]通过训练一组聚合器函数聚合局部邻域的特征来生成每个节点的单个嵌入,不足的是并没有继续通过转换节点邻域探索重构的图结构。Du等[19]将图神经网络拓展到局部特征以提取任意图结构数据,但该方法通过控制滤波器接受域来控制局部特征输入,导致了网络模型在整个输入图中过于关注相邻的图结构局部视角。

此外,已有研究[20-22]发现使用跨层的跳跃连接来加强浅层信息,可以加强浅层特征在架构中的表达能力和指导效率。Chen等[23]利用恒等映射和初始残差连接的组合扩充了模型的层数,保证了当模型叠加更多层时模型的浅层信息仍然可以被补充。Li等[24]利用残差连接[25]和扩张卷积[26]的结合,通过加强浅层信息的指导解决了模型梯度消失的问题。以上模型存在的问题是提取的浅层节点与深层更新节点没有做信息变换,因此并没有真正增加模型输入的多样性。

为解决上述问题,本文设计了基于随机重构图结构的图神经网络分类算法。原始图结构中自适应地融合kNN图结构,可以有效保持同类节点相似性。通过随机节点特征转换节点邻域信息,使重构图上的节点特征在传播过程中具有随机性,解决了节点对邻域依赖性高的问题。此外,模型对初始信息进行多支提取,额外的消息传递可以帮助图神经网络更好地吸收和嵌入浅层特征信息。

总之,基于随机重构图结构的图神经网络分类算法是重构图结构和随机特征结合的方法,整体框架上加入多支浅层特征,使模型更有效地完成节点分类任务。首先,原始图结构根据随机特征所得到的分数向量自适应地与kNN图结构信息融合,得到随机重构图。进一步,模型中加入基于层数自适应的多支浅层信息提取块,使模型随着层数的加深将更多浅层信息补充到图结构中。最后,提出的方法使用分类损失和自监督损失联合优化来学习模型参数。模型在半监督和全监督节点分类任务上取得较高精度,在数据集上的实验结果验证了所提模型的正确性和有效性。

1 基于随机重构图结构的图神经网络分类算法

1.1 前期准备

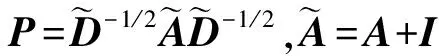
图相似度量学习:为了捕获特征空间中节点的图结构信息,基于节点特征矩阵构造kNN图,定义Ak为kNN图的邻接矩阵,Dk为kNN图的度矩阵。本文采用余弦相似性方法用两个节点的向量夹角的余弦值度量节点之间的差异。给定的节点对xi,xj,计算其余弦相似度为

(1)

根据相似度得分为每个节点选择k个最相似节点,建立节点之间的相关性,从而构造出kNN图结构。

1.2 整体网络框架

本文设计了基于随机重构图结构的图神经网络分类算法来保持同类节点相似性,并解决聚合过程中对节点对邻域依赖性高的问题,模型的概述如图1。首先,对原始图同时执行kNN构造k近邻图,以及随机特征变换得到随机特征,并根据权重值增强随机特征中保留的节点信息。其次,通过自适应特征融合和自适应自环学习完成图结构重构,从而自适应地调整节点特征之间的信息,完成节点特征的更新。最后,加入提取的多支浅层信息,通过对参数的控制实现当层数加深时补充更多的浅层信息。

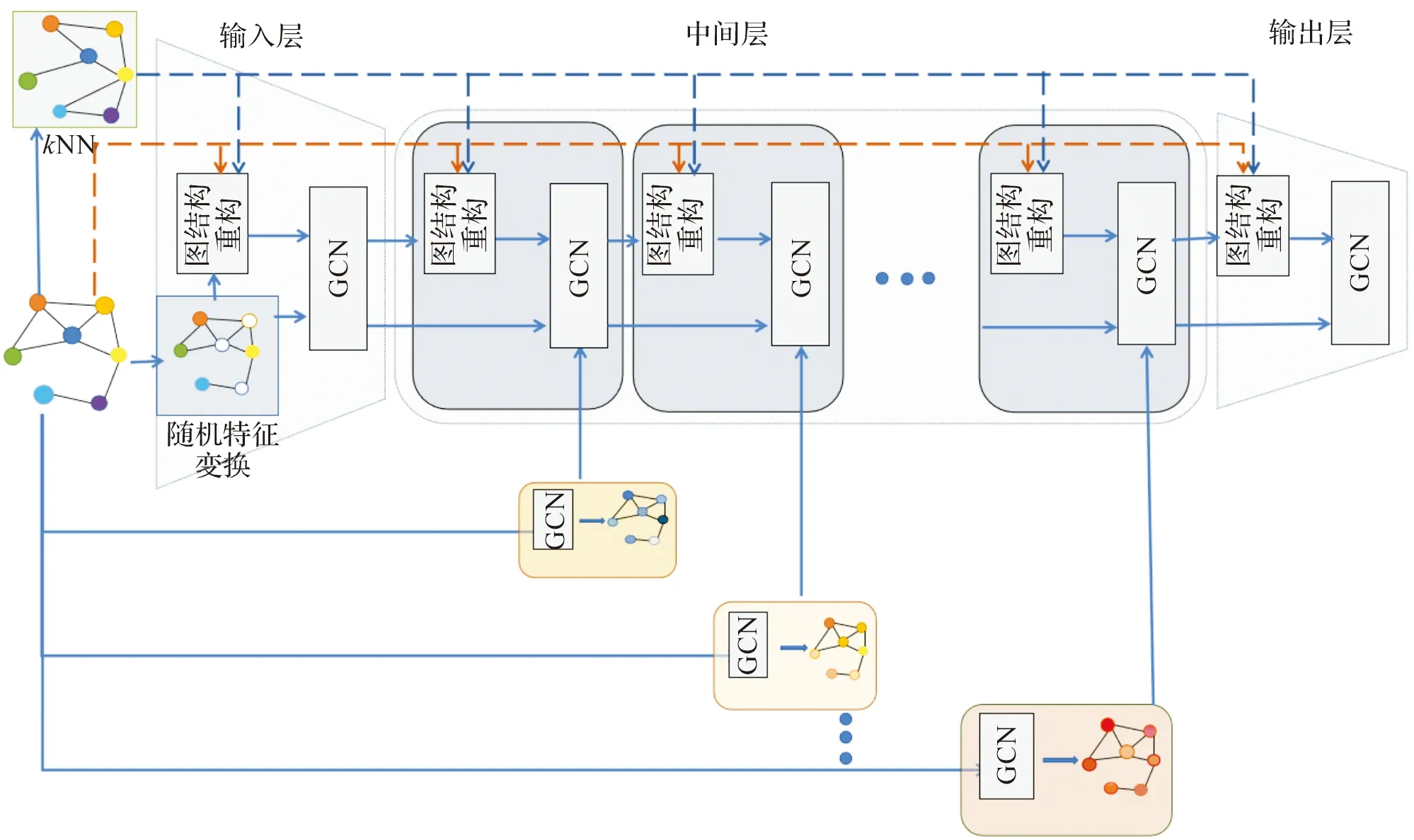
图1 基于随机重构图结构的图神经网络分类算法框架Figure 1 Framework for classification algorithm of graph neural network based on random reconstructed graph structure

多支浅层信息提取块:随着网络深度的增加,节点特征将逐渐收敛到相同的值,从而导致节点难以区分。为了提高节点分类性能,在模型中加入提取的多支浅层信息,其节点信息由参数α(l)控制,参数α(l)随着分支的数量递增,通过补充更多的浅层信息。在中间层中多支浅层信息的第l支特征定义为

(2)

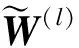
(3)

随机特征变换:随机特征变换转换了邻域节点信息,它控制着在聚合过程中特征与重构图结构的随机传播,随机特征变换如图2所示。随机特征变换有两个步骤。首先,节点特征与丢弃矩阵相乘,对节点信息进行部分丢弃;其中,丢弃矩

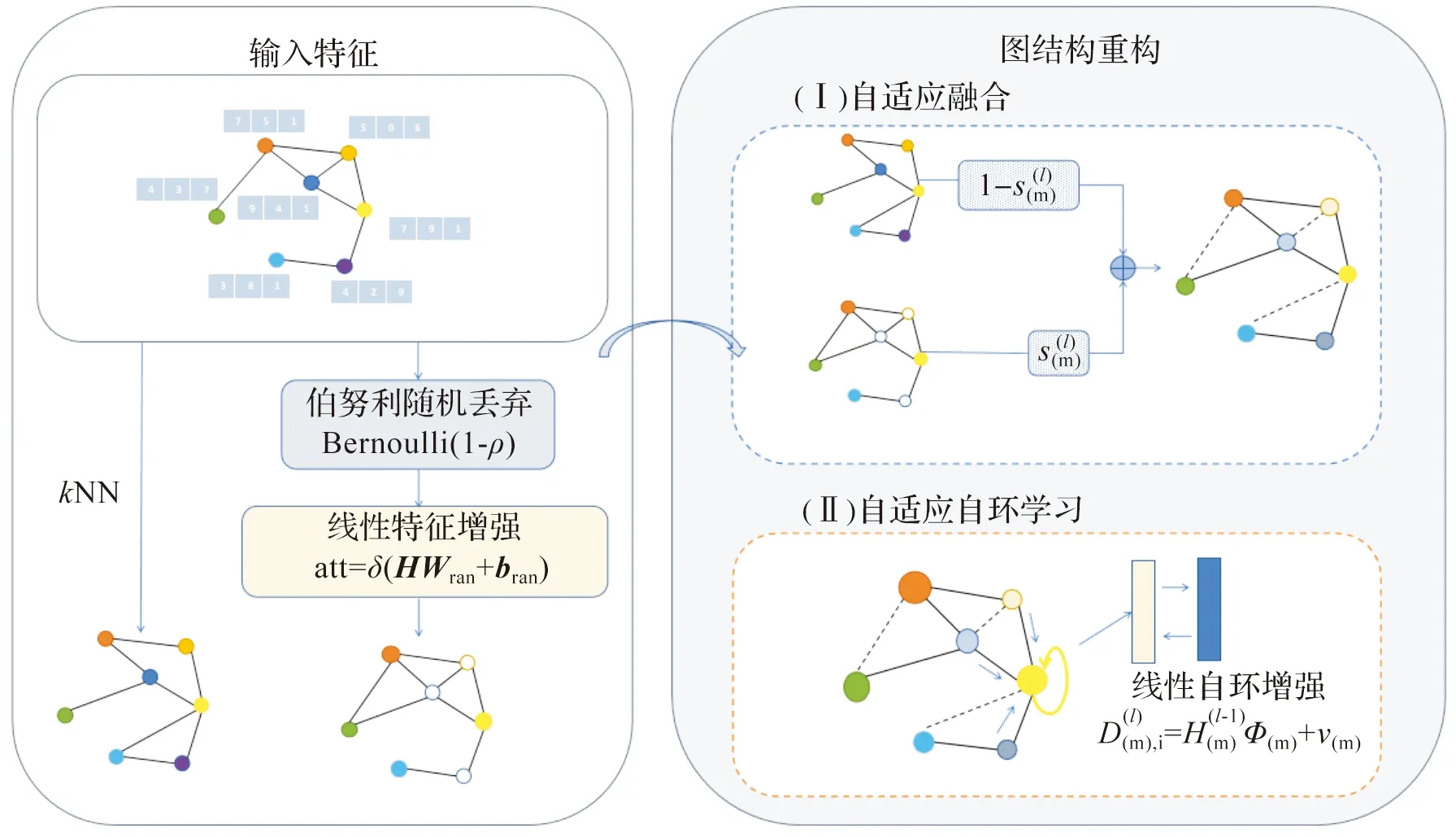
图2 输入层中随机图结构重构图Figure 2 Random graph structure reconstruction graph in the input layer

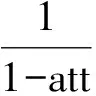
经过变换得到的随机特征为

(4)

式(4)中,θ=diag(k1,k2,…,kn)为丢弃矩阵,特别地,ki符合伯努利分布,即ki=Bernoulli(1-ρ),ρ为丢弃因子控制着初始特征的向量置零比例。att为根据初始特征计算的每个节点的权重系数,其表达式为

att=δ(HWran+bran)。

(5)

随机图结构重构:本文设计一种自适应融合机制,在图结构和节点特征融合时嵌入分数向量权重系数。原始图结构中融合kNN图可以加强节点之间的相关性,解决在传统特征聚合过程中节点相似性破坏的问题。在获得随机特征和kNN图之后,第k层的融合传播矩阵为

(6)

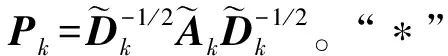
(7)

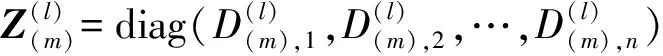
(8)

式(8)中,Φ(m)为自环权重矩阵,v(m)为自环偏置。重构图的传播矩阵为

(9)

(10)

1.3 损失函数

在文中的半监督和全监督任务中,为有效的保持节点的相似性,在其损失函数上设计一个分类损失和自监督学习损失的组合。

分类损失:针对节点分类任务对样本标签进行软化处理以获取更光滑的损失函数:

(11)

自监督学习损失:采用自监督学习策略[25],从给定的节点对的获取伪标签,预测节点之间的特征相似性,有效地保持特征和结构的相似性。其损失函数为

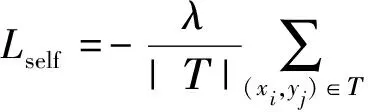
(12)

因此,该框架最终完整的损失函数为

L=Lclass+Lself。

(13)

2 实验及结果分析

2.1 数据集

本文的实验使用三个引文网络数据集:Cora、Citeseer和Pubmed。表1统计了实验中三个基准数据集的组成。

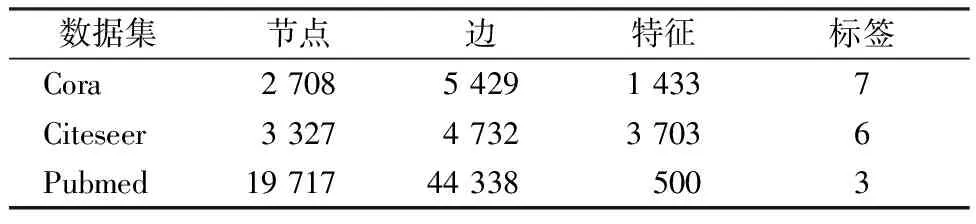
表1 实验中使用的数据集的统计数据Table 1 Statistics of datasets used in experiments

Cora是由机器学习相关论文组成的数据集。它有2708个样本点,每个样本点都有1433个特征。样本点表示科学论文,这些科学论文分为以下七个类别:1)基于案例;2)遗传算法;3)神经网络;4)概率法;5)强化学习;6)规则学习;7)理论。每个样本点都与其他样本点存在联系,因此样本点组成了一个连通的图。

Citeseer是一个关于论文之间引用或被引用的数据集,由3 327篇论文的图表组成。论文分为六类:代理、人工智能、数据库、信息检索、机器语言和HCI人机交互。数据集有两种文件:.content文件和.cites文件。

Pubmed是由19 717篇与糖尿病相关论文组成的数据集。Pubmed中的每篇论文都由TF-IDF加权词向量表示。TF-IDF表示评估其中一份文件的重要程度。

2.2 实验设置

实验以Python3.7作为实验环境进行网络的搭建和训练。实验以精度(Accuracy, A)作为节点分类的性能评估指标。本文对基准数据集进行半监督训练和全监督训练,对每个数据集里的文件进行训练、验证和测试。实验学习率为0.02,L2正则化系数设置为5e-4,线性层的丢弃率为0.8,隐藏层的神经元数量为128。本模型采用自适应学习率优化算法(Adaptive moment estimation,Adam)[28]训练网络。多支浅层信息的放大系数α取值范围为[1,5],随机特征的丢弃因子ρ取值范围为[0.1,1],自环的系数μ取值范围为[0.000 1,0.1],损失系数λ取值范围为[0.001,100]。本文给定取值范围验证集精度,为不同数据集和模型深度调整参数。

2.3 对比方法

为评估本文模型节点分类任务的成效,我们选取了具有代表性的基准图神经网络模型进行精度比较。首先,我们列出图卷积模型:GCNs[12]、图注意力网络(Graph Attention Networks,GAT)[10]、近似个性化传播(Approximate Personalized Popagation of Nural Pedictions, APPNP)[29]、GCNII[23]、跳跃知识网络(Jumping Knowledge Networks, JKNet)[30]。另外,在半监督任务中还增加比较了近几年的先进模型:自回归滑动图神经网络(Graph neural networks with convolutional arma filters, ARAM)[31]、节点相似性图卷积网络(Similarity Preserving Graph Convolutional Networks, SimP-GCN)[13]。最后,在全监督任务中还增加比较了近几年的先进模型:残差网络(Residual Network, ResNet)[21]、节点分类图正则神经网络(Neural Graph Learning-NodeNet, NodeNet)[32]、几何图卷积网络(Geometric Graph Convolutional Networks, Geom-GCN)[33]、边蒸馏(Link Distillation , LinkDist)[34]、和随机点对的对比蒸馏(Contrastive Training With Negative Links , CoLinkDist)[34]。本文采用4层的模型,为了公平起见,所有实验的默认网络层数均设置为4层,并且对三个数据集以同样的比例划分,进行相同的训练和测试。

2.4 实验结果

为全面的评价模型对节点分类任务的有效性,我们分别在Cora、Citeseer和Pubmed数据集做了半监督实验和全监督实验。

半监督实验如表2。对于三个基准数据集,我们将每个类的节点随机分割为60%的训练集、20%的验证集、20%测试集。SimP-GCN和GCNII模型都是半监督节点分类任务中实现先进性能的方法。从结果上看,GCNII和ARMA在卷积方式上的改进,使节点的更新学习方式更加高效。SimP-GCN加入kNN图结构信息保持了特征相似性,持续的提高了节点分类精度。本文模型在重构图结构的基础上使节点特征随机性传播,解决了节点对邻域依赖性高的问题,优化了特征聚合过程,使精度进一步提高。

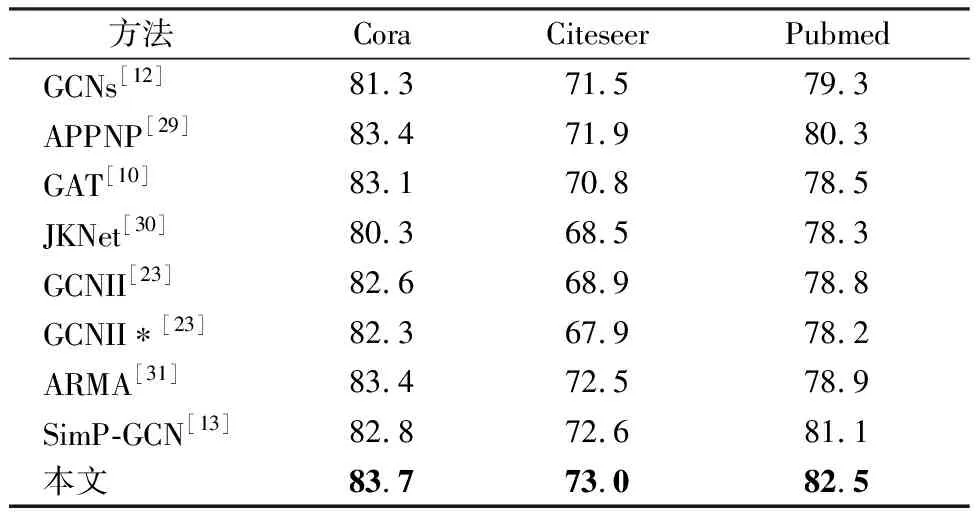
表2 半监督节点分类精度结果汇总

所提出方法在三个数据集上的全监督实验结果如表3。GCNII、JKNet、ResGCN为深层模型,其方法着力于解决过平滑问题,成功加深模型层数从而提高节点分类精度。本文模型在全监督节点分类的数据结果表明,当模型的层数为浅层时已表现出优越性,特别是其结果已优于其他模型在深层模型的结果。随机图结构在特征聚合过程中有效的保持了节点相似度,网络架构增加多支浅层提取,在特征更新时补充浅层信息,进一步了提升节点分类性能。

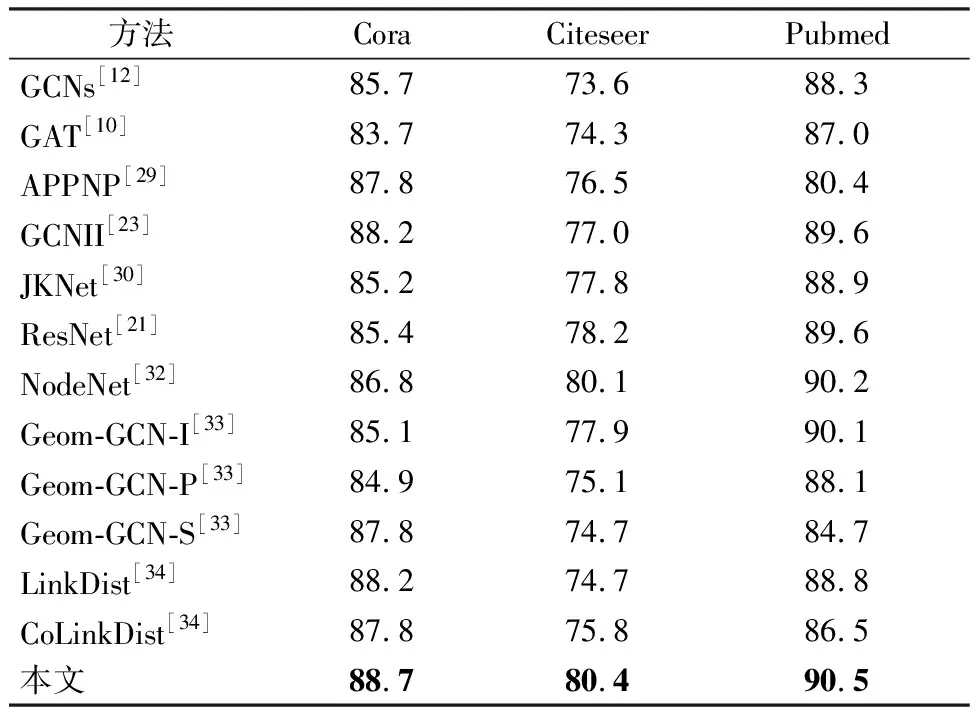
表3 全监督节点分类精度结果汇总

2.5 深度扩展模型

为了验证多支浅层信息对增加模型深度的作用,我们对模型深度进行了拓展,并对比了单支主干模型与添加多支浅层信息的模型在半监督实验上的节点分类性能。在Cora、Citeseer和Pubmed数据集进行2、4、8、16、32、64、128层的深层拓展实验。

根据图3实验结果表明,单支主干模型在层数超过4层时,精度发生明显的下降。其原因随着网络层数加深GCN遭受过平滑的问题。节点的特征将趋于收敛到相同的值,节点的区分度下降,后续的节点分类任务的性能降低。添加多支浅层信息的模型突破了4层以上的网络层数,精度在网络层数逐渐增加时仍然保持稳定的精度。本文模型通过通过多支浅层特征提取在进行特征更新时补充浅层信息,层与层之间的跳跃连接为模型梯度传播增加了额外的路径,对缓解过平滑问题起到了一定作用。

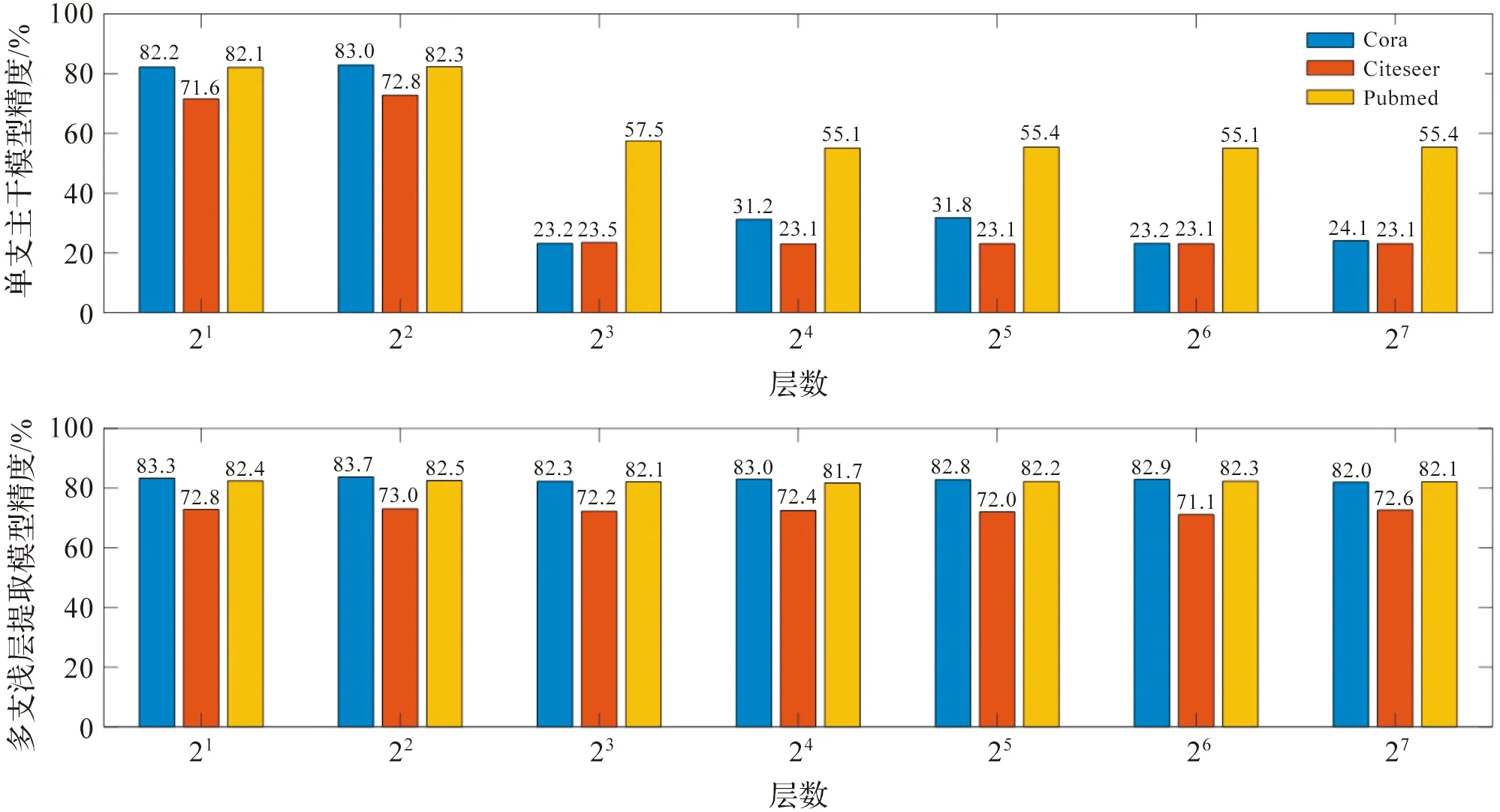
图3 不同深度的分类精度结果汇总Figure 3 Summary of classifification accuracy results with various depths

2.6 超参数讨论

本小节讨论了几个超参数取不同值时对节点分类的影响效果,结果如图4所示。我们研究了损失系数λ、自环系数μ、随机特征丢弃因子系数ρ、多支浅层信息的放大系数α这四个超参数取不同值时,对节点分类性能的影响。实验先选用初始化的模型参数,进一步逐一变换参数,以获得每个参数单独的影响效果。

图4 超参数实验节点分类精度结果汇总Figure 4 Summary of classifification accuracy results with hyperparameter experiment

损失系数调整了分类损失和自监督学习损失的贡献度。在Cora、Citeseer数据集上分类损失占主导作用,在Pubmed数据集上增加自监督学习损失的比例使结果精度进一步突破,因此损失系数λ在Cora、Citeseer、Pubmed三个数据集上分别选择为0.01,10,100。随机特征丢弃因子其变化程度评估模型的鲁棒性,在一定范围内对层传递的特征进行干扰时,节点分类精度没有明显的下降趋势,因此随机特征丢弃因子系数ρ在Cora、Citeseer、Pubmed三个数据集上分别选择为0.2,0.3,0.2。自环系数可以为单个节点调整不同的信息,因此自环系数μ在Cora、Citeseer、Pubmed三个数据集上分别选择为0.1,0.1,0.001。多支浅层信息的放大系数调节了每层加入浅层信息的比例,不同的系数对精度的影响说明浅层信息对模型的指导意义,因此多支浅层信息的放大系数α在Cora、Citeseer、Pubmed三个数据集上分别选择为3,2,2。

2.7 消融分析

本节讨论了模型中不同模块对实验性能的影响,构建了8组自身消融对比实验。我们在实验设置相同的条件下,对Cora、Citeseer、Pubmed数据集在原模型的基础上进行对比实验。实验结果如表4,表中“-”表示模型中不增加该模块,“√”表示模型中使用该模块。特别地,H表示直接输入初始特征,Hran表示对初始特征做丢弃和增强操作,融合机制表示将kNN和输入特征自适应融合。

表4 消融实验节点分类精度结果汇总Table 4 Summary of classifification accuracy results with ablation experiment

模型A结果精度不能优于模型B结果精度,这验证了学习图结构和节点信息都是必不可少的;模型C、模型D与模型E分别验证了随机特征中丢弃和增强的作用,通过结果表明单独使用其中一个模块并不如两者结合使用,验证了增强局部节点信息对协调图结构数据的重要性。模型F在kNN图结构信息和原始图结构融合过程加入自适应优化操作。它进一步支持了简单地结合结构和特征是不够的,验证了重构图结构融合过程的重要性;模型G为模型中每一层的图结构补充了多样性的浅层信息,并缓解网络加深过程中过平滑问题的发生;最后,模型H加入自监督损失函数,自监督学习策略可以捕获复杂特征的相似关系。

2.8 算法时间复杂度分析

在相同的实验条件下,在Cora、Citeseer、Pubmed 3个数据集上对比了本文模型与GCN每轮的实验时间,通过表5中的实验结果分析模型的算法时间复杂度。本文模型对节点进行相似度计算得到kNN图结构,并通过随机特征变换丢弃部分节点特征。这些操作虽然增加了模型的训练时间,但本文模型的精度得到了一定的提升。

表5 对比实验时间结果汇总Table 5 Comparison of experimental time results summary s

3 结 语

本文提出了基于随机重构图结构的图神经网络分类算法,以解决大多数GCNs在特征传播过程中出现相似性被破坏和节点过于依赖邻域的问题。首先,输入图根据随机特征得到的分数向量对原始图和kNN图两种图结构自适应地构造出随机图结构。然后,通过增加多支浅层信息提取单元优化网络架构,在特征更新时补充浅层信息。最后,在分类损失的基础上加入了自监督学习损失,更好地保持节点对的相似性,使节点分类任务的性能得到进一步提升。

本文在多个数据集的节点分类任务上分别做了半监督和全监督实验,实验结果均有0.9%～2.3%的提升。在未来,我们将有机会探索可变形的卷积层,构建每一层不同k值的kNN图结构,进一步挖掘图结构在图神经网络的潜力。