一种求解相关随机变量联合累积分布函数的方法

杨 永，李海滨

(内蒙古工业大学 理学院，内蒙古自治区 呼和浩特 010051)

联合概率累积分布函数是概率论中重要的概念，在工程结构可靠性分析中有着广泛应用.实际应用中，根据已有的一维函数模型，如正态分布、对数正态分布、极值Ι型分布、指数分布、威布尔分布等，能够容易得到边缘累积分布函数，对具有独立性的数据，联合累积分布函数可以通过边缘累积分布函数的直接相乘得到.但在工程中，所测得的数据往往存在相关性，如岩土工程抗剪强度参数中的黏聚力和内摩擦角、基桩荷载—位移双曲线等.为了能更好的进行可靠性分析，必须考虑数据间的相关性.

目前，为了计算方便，针对具有相关性的二维数据往往采用二维分布模型的方法，如二维正态分布[1]、二维对数正态分布[2]、二维指数分布[3]等.虽然这些二维分布模型能够考虑到数据间的相关性，但是必须满足边缘分布具有相同的分布类型，如二维正态分布要求其边缘分布均满足正态分布.但在实际工程中，数据往往不是同类型分布，因此二维分布模型的适用范围受到了极大的限制.对于这些非同类型分布，Nataf于1962年提出了Nataf分布模型[4]，有效地解决了一些相关非正态变量的联合概率分布问题，但是基于Nataf模型构造的二维联合累积分布函数依旧隐含着变量间的相关模型是Gaussian结构，因此还是很难解决工程问题中复杂边缘累积分布函数的问题.另外一种常用的构造方法是基于Pearson以及Spearman相关系数构造出联合累积分布函数，但是其只能描述数据间的线性相关关系，很难处理一些具有明显非线性特征的问题.针对现有构造联合累积分布函数存在的问题，寻找一种适用范围广、计算简便的新方法是一个亟需解决的问题.

1959年，Sklar指出，任意一个多维联合累积分布函数都可以分解为对应的边缘累积分布函数和一个Copula函数[4].Copula理论的提出为联合累积分布函数的构造提供了一个全新的途径，由于分开构造边缘累积分布函数和Copula函数，因此可以构造出任意边缘累积分布函数和任意相关结构的联合累积分布函数，而且对不同相关结构的数据，有多种Copula函数可以选择，如Gaussian Copula、t-Copula、Frank Copula等.由于Copula函数的优良性质，其在金融、水文、岩土等多个领域得到了广泛应用[5].而阿基米德Copula函数是所有Copula函数中最常用的一类函数，具有形式简单、对称性、可结合性等优点，而且只要找到“生成元”就可以构造出这一类函数.

目前已经有许多构造阿基米德Copula函数的方法，如Markov方法[6]、Laplace变换[7-8]等，但这些方法均有一定的局限性[9]，因此一些学者对阿基米德Copula生成元的复合构造进行了研究[10].在此基础上，文中提出了一种多参数Copula构造形式，并利用经验分布函数，通过采用正交距离回归算法进行曲线拟合的方法，对由此函数构造的联合累积分布函数进行拟合，从而实现了对联合累积分布函数的求解.

首先介绍了最常用的阿基米德Copula函数及其构造具有相关性的二维随机变量联合累积分布函数的方法，然后提出一种多参数Copula函数的构造方法以及对其构造的联合累积分布函数进行拟合和参数估计，最后利用算例对其有效性做出验证.

1 基于Copula理论的联合概率分布函数构造方法

Copula函数是对多元随机变量相关结构的一种刻画，可以理解成多元随机变量的联合累积分布函数和边缘累积分布函数之间联系的纽带[9].

1.1 Copula函数的定义

Copula理论最早由Sklar于1959年提出.Sklar指出，任意一个多维联合累积分布函数都可以分解为相应的边缘累积分布函数和一个Copula函数，该Copula函数确定了变量间的相关性，包括相关系数的大小和相关结构的类型.对于n维情形,根据Sklar定理，可将变量x1,x2,…,xn的联合累积分布函数F(x1,x2,…,xn)表示为：

F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn),θ)=C(u1,u2,…un;θ),

(1)

式中，ui=Fi(xi)为变量xi的边缘累积分布函数，同下文i=1，2，…,n；C(u1,u2,…un;θ)为Copula函数；θ为Copula函数的相关参数.

常用阿基米德Copula函数的具体形式为:

(2)

(3)

(4)

1.2 Copula函数的相关参数θ

Copula函数中的相关参数θ表征了变量间的相关性的大小，由于描述的是变量总体间的相关性，因此，需要借助极大似然理论来求出相关参数.用于对Copula函数进行参数估计的方法主要有最大似然估计法(ML估计)，分布估计(IMF估计)和半参数估计(CML估计)等[11-12].将采用半参数估计法也叫伪最大似然估计法进行参数估计，该方法通过采用样本数据各个变量的经验分布函数来分别取代其边缘累积分布函数，以此得出Copula函数的相关参数θ.以具有边缘分布F1(x1)和F2(x2)的二维联合累积分布函数为例：

由(1)得样本(x1i,x2i)，i=1,2,…，n的似然函数为:

(5)

其对数似然函数为:

(6)

对于(6)中的边缘累积分布函数值，采用经验分布函数值Femp代替，然后根据最大似然估计方法，求解出对数似然函数的最大值点，即可估计出相关参数θ.

(7)

1.3 Copula函数模型的拟合优度检验

判定选用的函数模型是否能够较好的描述变量之间的关系，需要对Copula函数进行拟合优度检验，理论上，统计学常用的变量分布假设检验方法均适用于Copula函数检验，如皮尔逊拟合优度χ2检验、Kolmigrov检验、正态W检验等[13].

文中采用Kolmigrov-Smimov(K-S)来检验Copula联合累积分布函数模型，用离差平方和准则(OLS)、赤池信息准则(AIC)对Copula联合累积分布函数模型进行优选.

以二维为例，K-S检验统计量D、离差平方和准则(OLS)、赤池信息准则(AIC)定义如下：

1) K-S检验统计量D

(8)

其中，Ci是样本数据xi=(x1i,x2i)的理论联合累积分布函数值；mi是二维数据样本数据中满足条件x1≤x1i,x2≤x2i的个数；n为样本数据量.

2) 离差平方和准则(OLS)

(9)

其中，

Femp(x1i,x2i)=p(x1≤x1i,x2≤x2i)，i=[1,n].

Femp(x1i,x2i)为经验分布函数值，C(u1i,u2i)为理论联合累积分布函数值.

3) 赤池信息准则(AIC)

(10)

AIC=nln(MSE)+2k,

其中，Femp(x1i,x2i)为经验分布函数值，C(u1i,u2i)为理论联合累积分布函数值，k为模型参数的个数.

2 一种乘积生成元构造的多参数Copula

不同的Copula函数用于描述具有不同相关特性的相关变量，在Copula函数中，阿基米德Copula函数是现在最常用也是最重要的一类Copula，由Genest和Mackey于1986年所提出，其函数表达式为：

C(u1,u2,…,un;θ)=φ-1(φ(u1)+φ(u2)+…+φ(un)),

(11)

式中φ(·)是阿基米德Copula的生成元，为满足固定边值的单调递减凸函数.

根据生成元不同，阿基米德函数可以分为多种不同的形式，本文选取其中最常用的Gumbel Copula函数、Clayton Copula函数、Frank Copula函数等3种函数，其生成元和函数具体形式如表1.

表1 阿基米德Copula函数及其生成元

2.1 一种多参数Copula函数的构造

由上文可知，在阿基米德Copula函数中只有一个相关参数θ.由相关理论可知，生成元的乘积仍为生成元.以二维函数为例，将上述表1中的3种生成元两两相乘得到3种新的乘积生成元列于表2.在表2中给出了各乘积生成元所对应的隐式Copula函数，其中θ1、θ2为待定的相关参数.与已有的阿基米德Copula函数相比，新构造的Copula函数相关参数增加到2个，但由于选用了双参数表示样本的整体相关性，所以函数为不容易显性化的隐函数，因此需要一种求解相关参数的新方法.

表2 乘积生成元及其隐式Copula函数

2.2 相关参数θ1、θ2的确定方法

曲线拟合是采用连续曲线去近似地刻画一些离散点的函数关系，是处理数据常用的方法之一.主要包括三方面的内容，一是确定需要拟合的数据样本点，二是选择合适的函数模型，三是选取算法确定函数模型中的未知参数.在2.1节中，已经给出了边缘累积分布函数与联合累积分布函数之间含有未知参数的函数模型，因此，只要确定拟合数据以及算法就可以确定相关参数θ1、θ2.

2.2.1 拟合数据

在统计学中，经验分布函数是对已有样本累积分布函数的一种估计，根据Glivenko-Cantelli定理，随着样本数的增加，经验分布逐步收敛于真实累积分布值，因此采用边缘分布的经验分布函数作为边缘累积分布函数.而对各个样本点处的联合累积分布函数值，同样可由联合经验分布函数代替.以前者为自变量，后者为因变量，即可构成拟合样本.以n组二维数据样本(x1,x2)为例：

边缘累积分布函数

(12)

其中，

{x11,x12,…，x1n}*表示集合{x11,x12,…，x1n}中不大于x1i的个数,

{x21,x22,…，x2n}*表示集合{x21,x22,…，x2n}中不大于x2i的个数.

联合累积分布函数：

(13)

其中，{(x11,x21),(x12,x22),…，(x1n,x2n)}*表示集合{(x11,x21),(x12,x22),…，(x1n,x2n)}中x1≤x1i且x2≤x2i数据点的个数.

2.2.2 正交距离曲线拟合

由于采用了经验分布函数，为考虑边缘经验分布函数代边缘累积分布函数所带来的误差，即自变量误差，所以文中算法选取正交最小二乘法.正交最小二乘算法又称正交距离曲线拟合，其与普通最小二乘的区别是考虑了函数拟合过程中自变量的误差，以正交距离的残差平方和极小为准则进行曲线拟合，使拟合结果从整体上达到拟合最佳[14].

正交距离回归(ODR)算法[15]通过在迭代过程调整拟合参数使变量残差的平方和最小.ODR中的残差不是观察值与变量的预测值之间的差异，而是从数据到拟合曲线的正交距离.拟合准则如下：

(14)

其中，f(xi+δxi,yi+δyi,β)=0i=1,……，n,wxi和wyi为自变量与因变量的权重系数，δxi、δyi为自变量xi和因变量yi的残差，β是拟合参数.

3 数值算例

算例1

随机生成100组数据点作为样本.其中，随机变量x1为正态分布，均值μ1=8，标准差σ1=2，随机变量x2也为正态分布，均值μ2=12，标准差σ2=3，相关系数ρ=0.8.确定随机变量x1，x2的联合累积分布函数.

1) 选取Clayton Copula，Frank Copula，Gumbel Copula函数构造变量x1,x2的联合累积分布函数，可以写成

F(x1,x2)=C(u1,u2;θ).

(15)

2) 通过样本数据，采取半参数估计法(CML估计)确定参数θ，求得参数θ值如表3所示.

表3 参数θ值

3)由式(3)可以得到x1,x2的联合累积分布函数为：

在此基础上，利用文中所提的构造多参数Copula函数方法确定联合累积分布函数.

同样利用上述得出的100组数据点，由2.2.1确定拟合样本，选用OriginLab软件中非线性曲线拟合，算法选择正交距离算法，设置算法权重系数均为0.5，参数初始值设为1，迭代一次得到相关参数θ1、θ2如表4所示.

表4 参数θ1、θ2的值

由表4可以得到x1,x2的联合累积分布函数为：

结果对比

选取显著性指标α=0.05，对上述6种函数进行K-S拟合检验，并利用OLS准则、AIC准则进行函数优选.结果对比如表5.

表5 结果对比

由表可知，文中所构造的3个函数均通过显著性水平检验，拟合效果也优于常用的3类阿基米德Copula函数.其中，③的准则计算值最小，所以③为最优联合累积分布函数.其表达式如前所示:

由于边缘分布为正态分布，为验证已有样本外数据的准确性，所以采用二维正态分布模型计算所得的理论值与上述6种函数计算结果做对比.随机生成一组数据，将二维正态分布函数理论值与上述6种函数所计算的值绘制成散点图，如图1.

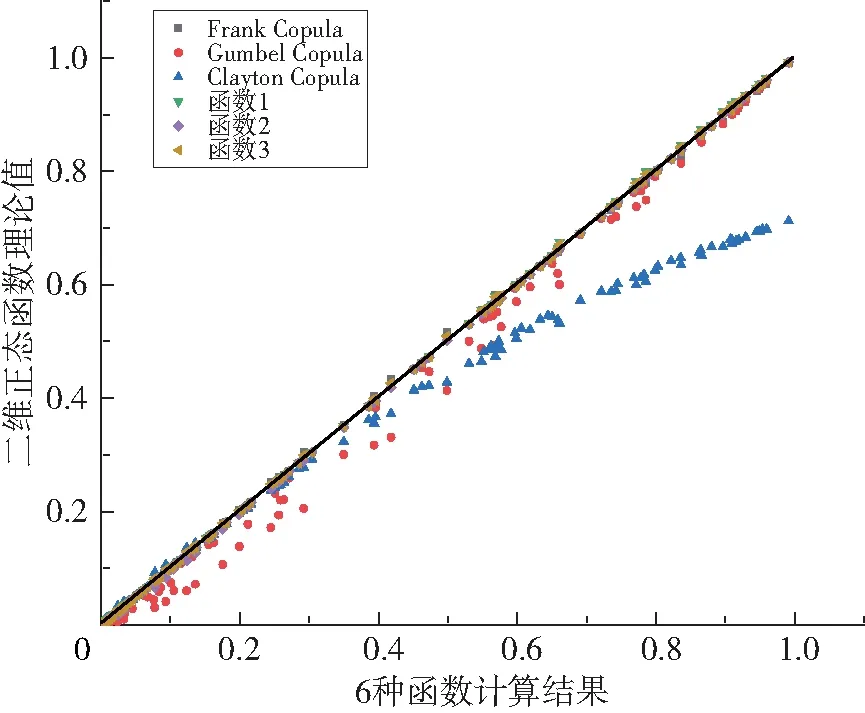
图1 二维正态分布理论值与6种函数结果对比图

图1所示，文中构造的函数①、②、③所绘制的散点均匀地分布在45°对角线附近，说明所构造的函数模型是合理的，也能更直观的看出其优于传统的阿基米德Copula函数.

算例2

现有沙颍河流域河南段干流下游周口水文站水文干旱特征变量统计结果，如表6.试根据表中数据构建水文干旱特征变量的二维联合分布模型.

根据表中数据，选取Frank Copula，Clayton Copula，Gumbel Copula以及所构造的3种函数①、②、③.其中，使用Kolmigrov-Smimov(K-S)来检验各联合累积分布函数模型，运用离差平方和准则(OLS)、赤池信息准则(AIC)对Copula联合累积分布函数模型进行优选.结果见表7.

表6 周口水文站水文干旱特征变量

续表6

表7 K-S检验结果

由表7可知，在显著性指标α=0.01的情况下，本文构造的联合累积分布函数①、②、③在D-S、D-P、S-P 3种情况下均通过了K-S检验，并且在OLS准则、AIC准则下均优于传统阿基米德Copula函数.

4 结语

Copula函数理论为构建相关性随机变量的联合累积分布函数提供了一种全新的途径，在已有理论的基础上，通过乘积生成元构造出了一种新的隐式Copula函数，实现了优于传统阿基米德Copula方法的拟合效果.针对隐函数中参数求解困难的问题，给出了一种基于经验分布函数和ODR拟合算法相结合的求解未知参数方法，从而实现了对联合累积分布函数的构建.最后，通过算例验证了本文所提方法的有效性，在K-S检验以及OLS准则、AIC准则中的表现优于传统阿基米德Copula函数，实现了对传统阿基米德Copula函数拟合精度的提高，由于是直接利用样本的经验分布函数，因此函数有更大的适用性，并且能随着样本数量的提高而自动改良函数的精度.