不同种植年限压砂地土壤水分吸渗特征与水力学参数

阮晓晗，白一茹，王幼奇，高小龙，钟艳霞

(1 宁夏大学 a 地理科学与规划学院，b 生态环境学院，宁夏 银川 750021；2 西北土地退化与生态恢复国家重点实验室培育基地，宁夏 银川 750021；3 西北退化生态系统恢复与重建教育部重点实验室，宁夏 银川 750021)

压砂地是西北干旱半干旱地区充分利用有限水资源、有效提高作物生产效率的独特旱作农业模式之一[1]。随着种植年限的增加，压砂地土石介质结构及砾石配比和含量等均发生了改变[2-3]，土壤增渗保墒功能逐渐退化[4]，甚至出现了土壤干燥化现象[5]。土壤水分是制约干旱半干旱地区农业发展的重要因子，土壤水力学参数是研究土体水分入渗过程、评价水分有效性、确定土壤持水能力等的基础指标[6-7]，对明确土壤水分运动过程、提高水分利用效率等有重要作用。土壤水力学参数主要包括土壤水分特征曲线、土壤饱和导水率、非饱和扩散率、土壤扩散率和比水容重等[8]，其不仅受土壤质地、水分、体积质量和孔隙等本身物理化学性质的影响，还受土壤的砾石量、粒径、厚度、植被类型和种植年限等外在因素的影响[9-10]。探究不同种植年限压砂地土壤水分吸渗特征及其水力学参数，对压砂地恢复产能、缓解干燥化现象及提升区域生态功能具有重要意义。

一般而言，土壤水分运动的饱和通量可以用渗透率或饱和导水率等参数来表征，但是实际上旱作农业模式下田间土壤水分长时间都处于非饱和状态[11]。土壤非饱和通量对于农业生产有重要实际意义，但难以直接检测，而饱和通量相对容易检测，因此在土壤水力学参数研究中推求非饱和通量成为研究的热点。当前土壤水力学参数的测算方法通常分为直接法和间接法。直接法一般包括野外测定法、实验室测定法[12]，其中野外测定法能够客观地反映土体渗透性的实际情况，但该方法存在操作复杂、工作量大、试验周期长、费用高等缺点；相比而言，实验室测定法较为便捷，但无法准确模拟现场条件，难以获取精确结果。由于土壤质地和环境条件的不同，其水分渗透特征会有所差异，异质性明显，因此通过土壤水动力学模型间接地研究和描述不同区域的不同土壤水分运移特征及水力学参数已引起许多学者关注。Shao等[13]、Wang等[14]分别基于一维水平土柱吸渗试验推求土壤Van Genuchten和Brooks-Corey模型参数，并取得了较好效果。Yang等[15]在一维水平土柱吸渗试验中发现，砾石含量和粒度对水力参数有显著影响，参数与岩石碎块含量呈线性关系。王幼奇等[16]利用一维垂直和水平吸渗试验研究了生物炭对黑垆土土壤水分运移特征的影响，发现土壤中添加生物炭会显著影响土壤水力学参数。单鱼洋等[17]通过一维水平土柱吸渗试验发现，不同矿化度微咸水入渗过程中，土壤水分运动参数发生了改变。综上可知，一维水平吸渗试验可以较精确地推求土壤水力学参数，且具有广泛的适用性。目前，针对压砂地土壤水分吸渗特征及非饱和扩散率等非饱和通量的研究较为缺乏，因此有必要对不同种植年限压砂地土壤的水分运动特征进行研究并推求其水力学参数，以明晰不同种植年限压砂地的水力学特征。

本研究采用室内模拟方法进行一维水平土柱吸渗试验，模拟不同种植年限(2，5，10，20，30和40 a)压砂地土壤吸渗过程，获取湿润锋深度和累积入渗量，用Philip和Green-Ampt入渗模型计算参数，并采用Brooks-Corey模型进一步推求不同种植年限压砂地进气吸力和水分扩散率等水力学参数,以及水分特征曲线和非饱和扩散率曲线，以期明确不同种植年限压砂地土壤水力学特征，为水资源的合理利用提供理论依据。

1 材料与方法

1.1 研究区概况

研究区位于宁夏回族自治区中卫市兴仁镇(105°22′E，36°76′N)，地处宁夏中部干旱带，属干旱半干旱气候，海拔1 680 m左右，年平均温度13.4 ℃，日照时数2 990 h/年，年平均降水量240～260 mm，年蒸发量3 200 mm左右，无霜期172 d左右。光热资源十分丰富，昼夜温差大，是硒砂瓜主产区。土壤类型为灰钙土，土壤砂粒、粉粒和黏粒平均含量分别为27.19%，62.52%和10.26%，属粉壤土；土壤有机质、全氮、全磷和全钾平均含量分别为6.53，0.51，0.59和17.94 g/kg。覆盖砾石来自香山风化碎石，覆盖厚度为15～25 cm。

1.2 试验材料

2020年10月，在研究区内根据不同种植年限压砂地实际分布面积及比例，在不同种植年限(2，5，10，20，30和40 a)压砂地分别均匀选取样点，共计100个样点。在各样点随机选取长×宽为100 cm×100 cm小区，采集小区砾石覆盖层(0～25 cm)全部砂石，将其风干后用孔径分别为50，31.5，25，16，10，5和2 mm筛子逐层过筛，对不同粒径的砾石称质量。将覆盖砾石去除杂质和土壤后，清洗、晾干备用。去除各样点表层覆盖砾石后，采集0～60 cm土层土壤，清除杂质后自然风干，研磨后过孔径2 mm筛备用。不同种植年限压砂地土壤基本物理性质如表1所示。

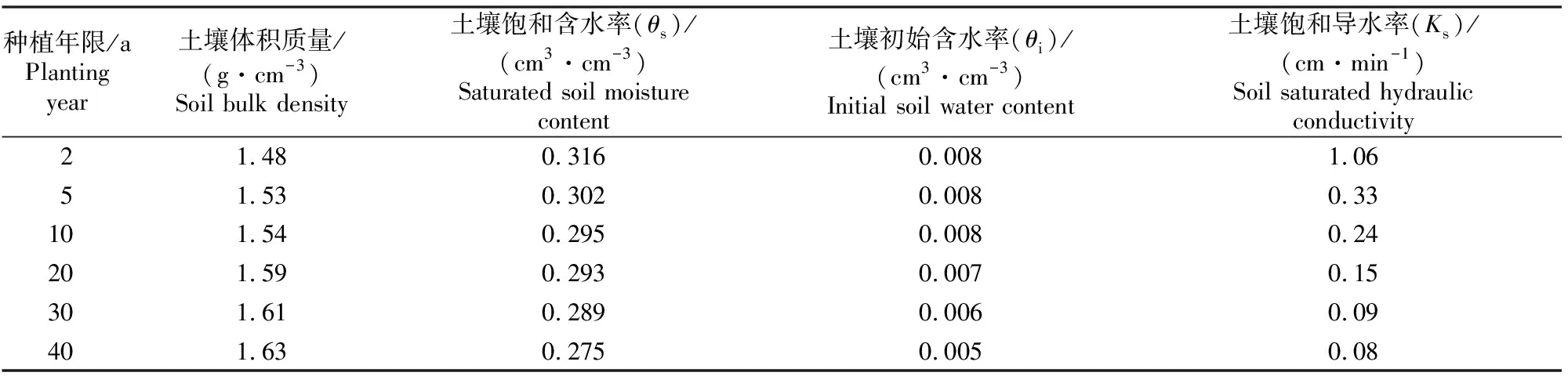
表1 研究区不同种植年限压砂地土壤基本物理性质 Table 1 Basic soil physical properties of gravel-sand mulched fields with different planting years

1.3 试验方法

试验于2020年10月在宁夏大学环境科学与工程实验室进行，采用室内模拟方法进行一维水平土柱吸渗试验，模拟不同种植年限(2，5，10，20，30和40 a)压砂地土壤水分吸渗过程。一维水平土柱吸渗装置(图1)由供水装置和水平土柱组成，供水装置选用与水平土柱同等规格(内径10 cm，高50 cm)的马氏瓶作为容器，在吸渗过程中时刻保持供水状态。水平土柱前端是一长3 cm的储水室，储水室上下分别设有外径为1 cm的通气孔和排水口，前端设有进水管用以连通马氏瓶，后端是一水平距离为50 cm的开口有机玻璃柱，储水室与水平土柱之间用均匀布有2 mm小孔的法兰连接。填装土柱时按照表2中不同种植年限压砂地砾石覆盖层砾石粒径配比填装砾石覆盖层，分层(5 cm一层)填装15 cm。然后按照当地不同种植年限压砂地实际测得的土壤体积质量(表1)填装土层，分层(5 cm一层)填装30 cm，土层与土层之间进行打毛处理。砾石覆盖层与土层深度共计45 cm。试验开始前，调节马氏瓶与水平柱相对高度,使马氏瓶出水口与储水室最上面持平，同时关闭进水口阀门。试验开始后，先打开进水口阀门，通过马氏瓶向储水室迅速注水，等储水室充满水后迅速关闭储水室阀门，记录马氏瓶水位的初始刻度，吸渗过程中分时间段读取不同时刻马氏瓶水位刻度及湿润锋刻度，在前5 min内每隔10 s记录1次，5～8 min每30 s记录1次，8～15 min每1 min记录1次，15～30 min每5 min记录1次，30～60 min每10 min记录1次，60～240 min每30 min记录1次，之后每隔60 min记录1次，当湿润锋运移到45 cm时停止供水，试验结束。以马氏瓶水位变化计算土壤累积入渗量及入渗速率，以湿润锋刻度变化表示湿润锋深度。

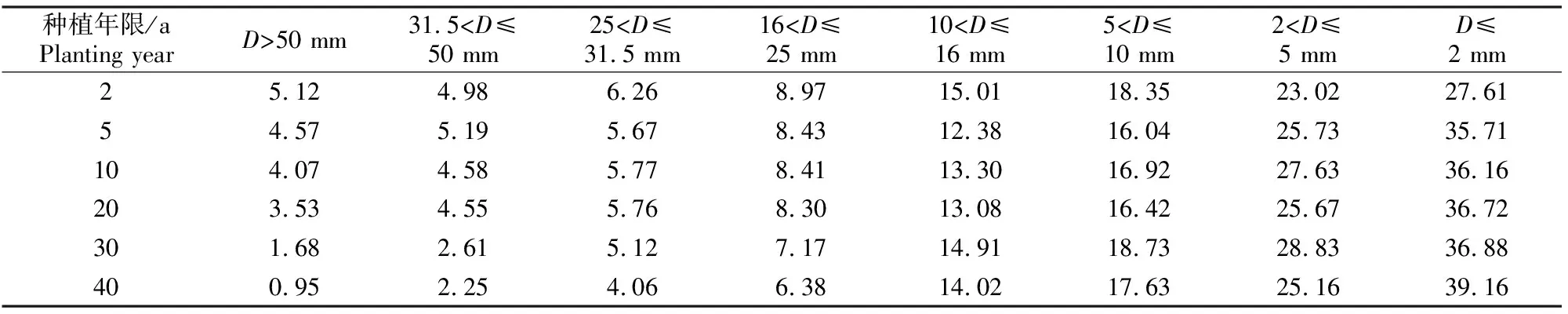
表2 研究区不同种植年限压砂地砾石粒径(D)配比

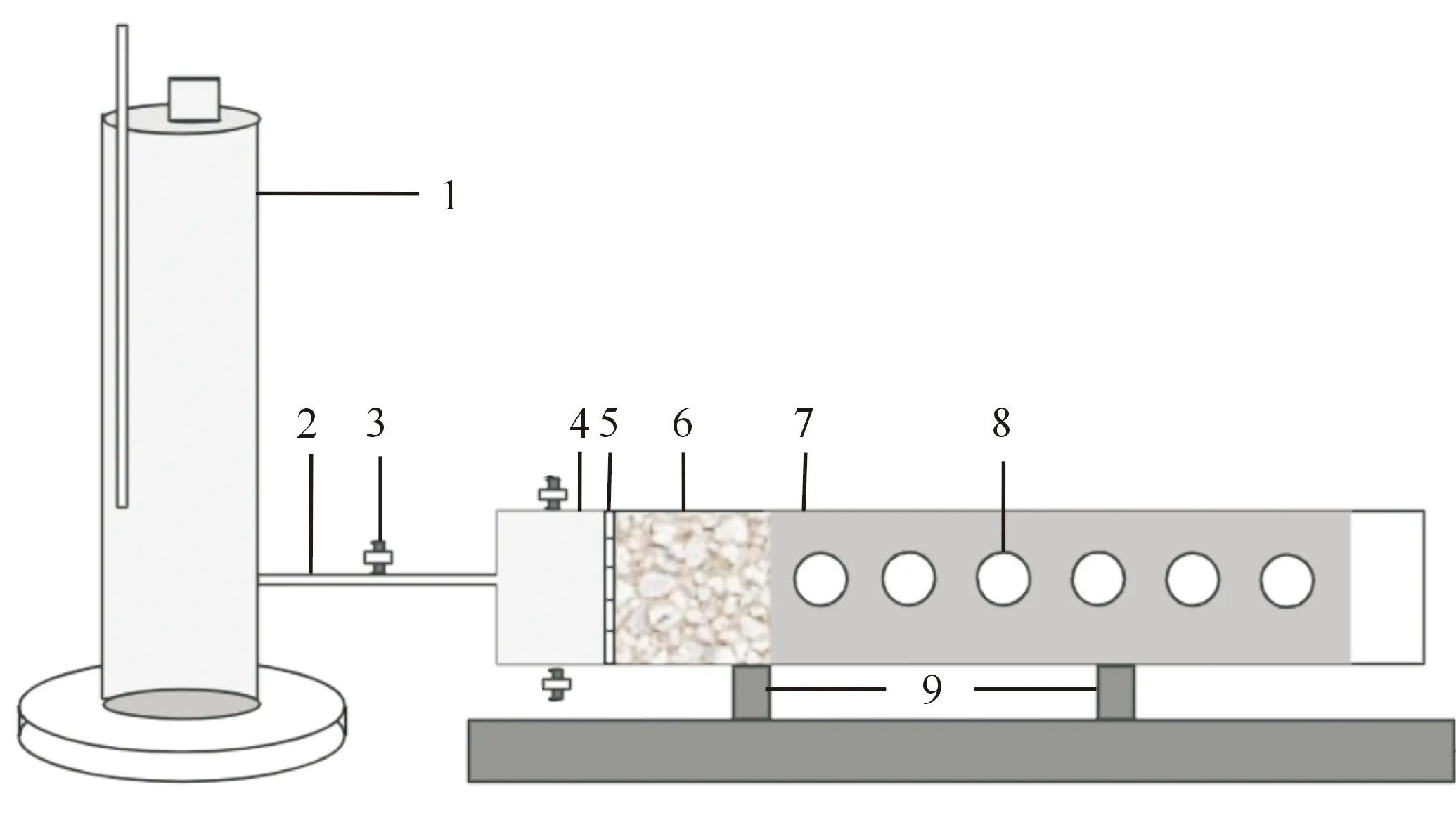
1.马氏瓶；2.进水口；3.阀门；4.储水室；5.法兰；6.砾石层；7.土层；8.取土孔；9.水平支架1.Mariotte bottle；2.；3.Valve；4.Water storage chamber；5.Flange；6.Gravel layer；7.Soil layer；8.Sampling hole；9.Horizontal support图1 一维水平土柱吸渗试验装置Fig.1 One-dimensional horizontal soil column absorption device

1.4 土壤水分吸渗模型参数

分别采用Philip模型[18]和Green-Ampt模型[19]来拟合不同种植年限压砂地土壤水分的吸渗特征。

Philip模型为：

I=St0.5。

(1)

式中：I为累积入渗量，cm；S为吸渗率，cm/min0.5；t为吸渗时间，min。

Green-Ampt模型为：

(2)

式中：i为吸渗速率，cm/min；Ks为土壤饱和导水率，cm/min；Zf为湿润锋深度，cm；Sf为湿润锋面吸力，cm；H0为土柱表面积水深度，cm。

由于土柱吸渗试验是在一维水平条件下进行的，因此忽略重力势能的影响，式(2)可以简化为：

(3)

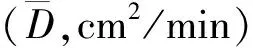
(4)

式中：θs为土壤饱和含水率，cm3/cm3；θi为土壤初始含水率，cm3/cm3。

1.5 土壤水力学参数模型

Brooks-Corey模型反映了土壤含水率、水吸力、饱和导水率及非饱和导水率之间的关系，可拟合土壤水分特征曲线和水力学参数，其表达式如下：

(5)

(6)

式中：Se为土壤有效饱和度；θ为土壤含水率，cm3/cm3；θr为土壤滞留含水率，当土壤初始含水率较低时，认为滞留含水率与初始含水率相等，cm3/cm3；hd为进气吸力，cm；h为土壤水吸力，cm；n为形状系数；K(h)为非饱和导水率，cm/min；m为经验参数，m=3n+2。

参考文献[14]，根据一维水平吸渗试验推求Brooks-Corey模型参数，计算公式如下：

(7)

(8)

(9)

式中：a为参数，当土壤初始含水率很小时，近似为1；A1、A2为参数，可以由一维水平土柱吸渗试验中的累积入渗量(I)、吸渗速率(i)和湿润锋深度(Zf)拟合获得。

A1=Zf/I，

(10)

A2=Zfi。

(11)

参考文献[21]，利用Brooks-Corey模型与一维水平吸渗控制方程来推求土壤水分饱和扩散率和非饱和扩散率，计算公式如下：

(12)

(13)

(14)

式中：Ds为土壤饱和扩散率，cm2/min；L为参数；D为土壤非饱和扩散率,cm2/min。

2 结果与分析

2.1 不同种植年限压砂地土壤水分的吸渗特征

根据一维水平土柱吸渗试验获取不同种植年限压砂地土壤水分累积入渗量及湿润锋深度随吸渗时间的变化，结果见图2。图2显示，相同吸渗时间下，随着种植年限的增加，湿润锋深度、累积入渗量均呈减小趋势，表明土壤水分入渗能力明显降低。各种植年限土壤的水分累积入渗量均随着吸渗时间的延长而增加，但不同吸渗时间下累积入渗量的增幅有差异，其中在初始吸渗阶段(0～60 min)累积入渗量增幅均较大，进入稳渗阶段(60 min以后)后增幅均较小。试验结束时，与种植2 a的压砂地相比，种植5，10，20，30和40 a压砂地土壤水分累积入渗量分别减小了4.36%，5.82%，7.04%，8.88%和12.48%。可知累积入渗量与吸渗时间呈正相关，与种植年限呈负相关。

图2显示，随着吸渗时间的延长，各种植年限土壤湿润锋深度均呈增加的趋势。在吸渗初始阶段，各种植年限压砂地土壤湿润锋深度差异不大，之后随着吸渗时间的继续延长，土壤湿润锋深度差异增大。试验结束时，与种植2 a的压砂地相比，种植5，10，20，30和40 a压砂地土壤湿润锋深度达到最大(45 cm)时所需的时间分别增加了37.50%，87.50%，106.25%，125.00%和137.50%。

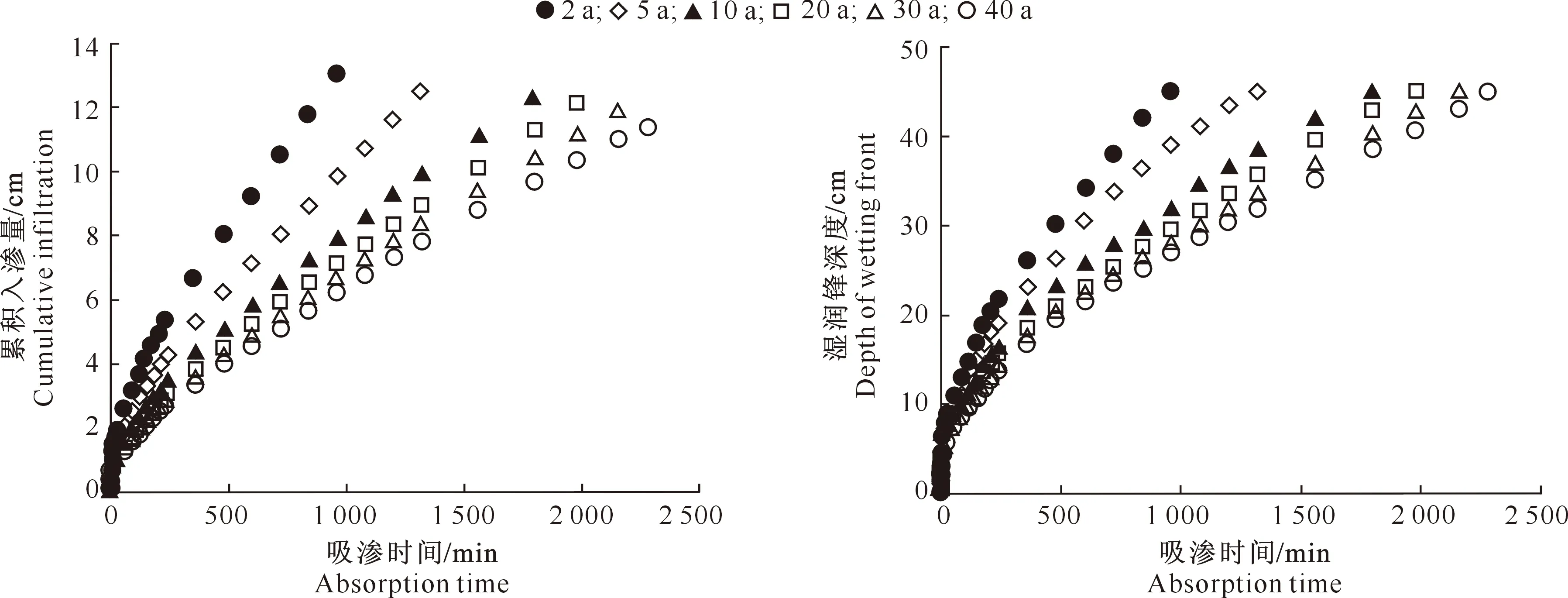
图2 不同种植年限压砂地土壤水分累积入渗量和湿润锋深度随吸渗时间的变化Fig.2 Variation of cumulative infiltration and depth of wetting front with absorption time of gravel-sand mulched fields with different planting years

2.2 基于Philip和Green-Ampt模型的不同种植年限压砂地土壤水分吸渗参数

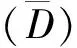
表3 基于Philip和Green-Ampt模型的不同种植年限压砂地土壤水分吸渗参数Table 3 Soil moisture absorption parameters of gravel-sand mulched fields with different planting years based on Philip and Green-Ampt model

2.3 基于Brooks-Corey模型的不同种植年限压砂地土壤水力学参数

采用Brooks-Corey模型获取不同种植年限压砂地的土壤水力学参数，结果见表4。由表4可知，A1、A2随种植年限的增加总体上均呈减小趋势，表明随着种植年限的增加，土壤湿润锋运移至相同深度时，累积入渗量逐渐减小，且吸渗速率逐渐减慢。由表4还可知，与种植2 a压砂地相比，种植5，10，20，30和40 a压砂地土壤水分的hd分别减小了1.22%，42.81%，46.37%，55.94%和64.97%，Ds分别减小了27.83%，68.54%，85.40%，90.57%和93.15%。随着种植年限的增加，hd、n和Ds均呈减小趋势，参数L无明显变化规律。

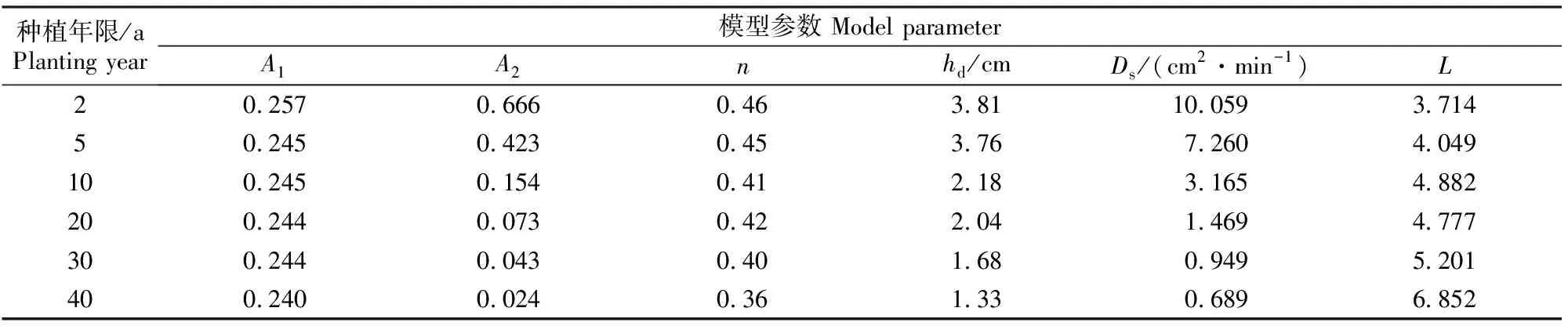
表4 基于Brooks-Corey模型的不同种植年限压砂地土壤水力学参数Table 4 Soil hydraulic parameters of gravel-sand mulched fields with different planting years based on Brooks-Corey model

2.4 种植年限对土壤水分特征曲线和非饱和扩散率的影响

土壤水吸力又称水势，是指土壤水的负压力，可表征土壤基质对水分的吸附能力[23]。非饱和扩散率是分析非饱和状态下土壤水分传导能力的重要参数之一，反映了在水平方向上土壤水分的运移轨迹以及含水量随时间的变化情况[8]。为了进一步明确不同种植年限对土壤水分特征曲线和非饱和扩散率的影响，将表4中的参数代入公式(5)和(14)中，可获得不同种植年限压砂地土壤水吸力(h)及土壤非饱和扩散率(D)与土壤含水率(θ)的关系。由图3可以看出，土壤水吸力随着含水率的增加而迅速降低，种植年限越长水分特征曲线降低越快，且在相同土壤含水率下，种植年限越大，土壤水吸力越小，土壤持水能力越差。此外，当h为1 000 cm时，不同种植年限压砂地土壤的含水率由大到小表现为2 a(0.034 cm3/cm3)>5 a(0.025 cm3/cm3)>10 a(0.024 cm3/cm3)>30 a(0.023 cm3/cm3)>20 a(0.022 cm3/cm3)>40 a(0.016 cm3/cm3)，可知在土壤水吸力相同的条件下，种植年限越大，土壤含水率越低。

由图4可以看出，D随着θ的增加而增大，且种植年限越小D增长越快；当θ为0.3 cm3/cm3时，与种植2 a压砂地相比，种植5，10，20，30和40 a压砂地的D分别减小了33.25%，67.45%，84.42%，89.06%和88.05%，可知在相同土壤含水率下，随着种植年限的增大，土壤非饱和扩散率整体呈减小趋势。

3 讨 论

土壤水分入渗特性是研究土壤水分有效性、确定灌溉定额和推广节水灌溉理论的重要依据之一[24]。本研究中，相同吸渗时间下，随着种植年限的增加，湿润锋深度、累积入渗量均呈减小趋势，表明土壤水分入渗能力明显降低。其原因主要是随着种植年限的增大，压砂地砾石覆盖层的土石混合配比发生了改变，粒径小于5 mm的砾石及细土比例增多，减小了土壤孔隙数量，导致水分在砂层和土壤中滞留的时间增加，从而使进入下层土壤的水分减少。此外，随着种植年限的增加，压砂地土壤体积质量逐渐增大，土壤变得紧密坚实，土石混合介质中孔隙数量逐渐减少，内部连通性变差，当土体湿润后膨胀会导致土体内部的孔隙进一步减小，土体中气体排出困难，从而使土壤水分吸渗受到了较大的气相阻力，吸渗过程变慢。李涛[25]等、张宏媛等[26]和李卓等[27]的研究均表明，土壤孔隙度减小、土壤体积质量增大能显著减慢土壤水分入渗过程，降低土壤水分入渗能力，这与本研究结果一致。

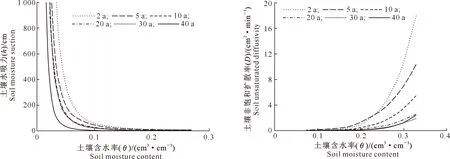
图3 不同种植年限压砂地土壤水吸力与含水率的关系Fig.3 Soil moisture characteristic curves of gravel-sand mulched fields with different planting years

土壤水力学参数对于灌溉调度、农田土水分运动过程以及田间或流域尺度的水平衡等研究非常重要[28]。本研究中，随着种植年限的增加，压砂地土壤θs、Ks、hd、Ds均呈减小趋势，即土壤导水、导气、持水能力和水分扩散能力变差。这是由于随着种植年限的增加，压砂地土壤压实程度增大，导致土壤结构变差；此外，在作物根系长期吸水的作用下，土壤干燥化程度加剧，从而出现了土壤体积质量变大、孔隙度变小、易板结的现象，使得土壤水分的扩散和传输受到了明显的阻滞。由本研究的土壤非饱和扩散率曲线可知，当土壤含水率较低时，土壤非饱和扩散率趋近于0，当土壤含水率增大到一定程度后其水分才开始扩散，并且土壤非饱和扩散率随着含水率的增大而明显增加。这主要是因为在土壤水分吸渗过程中，渗入土壤的水分首先被土壤颗粒表面吸持成为膜状水，当膜状水饱和后再进入土壤细小孔隙，然后才成为自由水继续扩散[20]。由本研究的土壤水分特征曲线可知，相同土壤含水率下，种植年限越长，土壤水吸力越弱，持水能力越差。这是由于种植年限越长，土壤体积质量越大、孔隙度越小，导致土壤结构及持水性能明显退化。José等[29]研究也发现，与免耕土壤相比，长期耕作土壤结构更加紧密，土壤持水性能更差，这与本研究结果一致。

本研究采用一维水平土柱吸渗试验，基于Brooks-Corey模型获取了不同种植年限压砂地土壤的水力学参数，该参数在一定程度上反映了不同种植年限压砂地土壤的水分运动状况。在将来的研究中，应结合一维水平土柱吸渗试验和Van Genuchten模型，获取更多具有物理意义的水力学参数，以便于明晰水分特征曲线变化机理。

4 结 论

1)在相同吸渗时间下，随着种植年限的增加，湿润锋深度、累积入渗量均呈减小趋势，可知种植年限的增加减缓了土壤水分吸渗过程，土壤水分入渗能力明显降低。

2)在Philip模型中，不同种植年限压砂地土壤水分吸渗过程中的吸渗率差异较大，表现为2 a(0.564 cm/min0.5)>5 a(0.412 cm/min0.5)>10 a(0.258 cm/min0.5)>20 a(0.178 cm/min0.5)>30 a(0.135 cm/min0.5)>40 a(0.097 cm/min0.5)。Green-Ampt模型中，土壤水分扩散率 随着种植年限的增加而减小。

3)Brooks-Corey模型中，种植年限对压砂地土壤水力学参数有明显影响。随着种植年限的增加，进气吸力和土壤饱和扩散率均呈减小趋势。在相同含水率条件下，随种植年限的增加，土壤水吸力和非饱和扩散率均减小，持水能力降低。