面向短时地铁客流量预测的混合深度学习模型

彭桐歆，韩 勇，王 程，张志浩

（1.中国海洋大学信息科学与工程学院，山东青岛 266100；2.青岛海洋科学与技术国家实验室区域海洋动力学与数值模拟功能实验室，山东青岛 266237；3.青岛市市北区党建引领基层治理推进中心，山东青岛 266000）

0 概述

随着传感器技术的飞速发展，记录人们日常行为的城市时空大数据如公交卡数据、出租车轨迹等越来越丰富。这些数据可以模拟和预测人类的活动模式，揭示人类社会活动及其运动规律，为构建智能交通系统（Intelligent Transportation System，ITS）提供可靠支持。通过分析地铁站的历史刷卡记录，对不同站点的短时客流量进行预测，不仅能方便出行者规划线路，而且能为管理部门调度车次提供依据，对促进智慧城市的建设具有重要的现实意义。

城市交通客流量预测的研究历程可归结为统计学方法、传统机器学习方法和深度学习方法3 个阶段。统计学方法包括差分整合移动平均自回归模型（Autoregressive Integrated Moving Average Model，ARIMA）［1］及其变体模型［2-3］、逻辑回归模型（Logistic Regression，LR）［4］、卡尔曼滤波［5］等。统计学方法能捕获时空序列中的线性特征，但对数据中的非线性特征却无法提取。因此，研究人员引入了传统机器学习方法，传统机器方法包括决策树、聚类、贝叶斯方法、支持向量机、最大期望算法、Adaboost、人工神经网络等。ZHANG 等［6］采用支持向量机（Support Vector Machine，SVM）对交通流量进行预测，LI等［7］融合季节性ARIMA和SVR 对地铁客流量进行预测，取得较好的结果。此外，还有不少研究人员在交通客流量预测上采用贝叶斯方法［8］、BP 神经网络［9］、随机森林［10］等方法，均取得了良好的结果。

然而在大数据时代，复杂且庞大的时空数据使建立特征工程的难度增加。相比统计学和传统机器学习方法，深度学习属于机器学习的一个分支，它利用深度神经网络来解决特征表达的过程。深度神经网络是一种相对特殊的神经网络，它包含较多的隐含人工神经网络层，可以学习复杂的非线性关系，以减小特征工程的复杂度。ZHAΟ 等［11］利用长短期记忆（Long Short-Term Memory，LSTM）网络进行交通流量预测。LI 等［12］提出基于残差LSTM 的交通流量预测方法，显式建模特征维度之间的依赖关系。ZHANG 等［13］利用结构相对简单的门控循环单元（Gated Recurrent Units，GRU）预测交通流。ZHANG等［14］将城市范围的时空流量序列表达为规则格网数据，以小时、天和周的周期提取历史观察值，并送入多层卷积神经网络（Conventional Neural Networks，CNN）进行建模。ZHAΟ 等［15］提出混合深度学习模型ResNet-CNN1D，对青岛市地铁客流量进行建模预测。

在现有的研究中，单纯使用循环神经网络（Recurrent Neural Networks，RNN）［16-17］只能捕获数据的时间特征，使用单一的CNN［18-19］只能捕获数据的空间特征，部分模型缺乏对流量数据时空特征的捕获，且忽视了历史周期片段对目标时刻的影响。此外，现有研究主要集中在如何将深度学习模型应用于短时交通流量预测，忽略了对模型的优化研究。交通流量典型的特征之一是交通峰值，现有模型对峰值的捕捉能力不够，极少关注天气、空气状况等多源外部信息。

为精准预测短时地铁客流量，本文构建一种混合深度学习模型ResGRUMetro，通过融合残差神经网络（Residual Neural Network，ResNet）提取交通流量的空间特征，运用GRU 提取流量的时间特征。该模型将近邻、日、周周期模式的时间片流量数据作为输入，利用混合深度学习模型挖掘数据的时空特征，使用加权平方误差（Weighed Square Error，WSE）对模型损失函数进行改进，加大对交通流量序列峰值处误差的惩罚，提高模型对交通流量中峰值的预测能力。此外，模型耦合天气、空气质量、节假日等外部因子，改进模型整体预测精度，得到目标时刻所有站点的客流量预测结果。

1 问题定义

本文拟解决的问题为利用混合深度学习模型对特定时间片的地铁客流量作精准预测。地铁客流量受历史时段客流量的影响，也受天气等外部因素的影响，该预测问题如图1 所示，可用公式表示为：

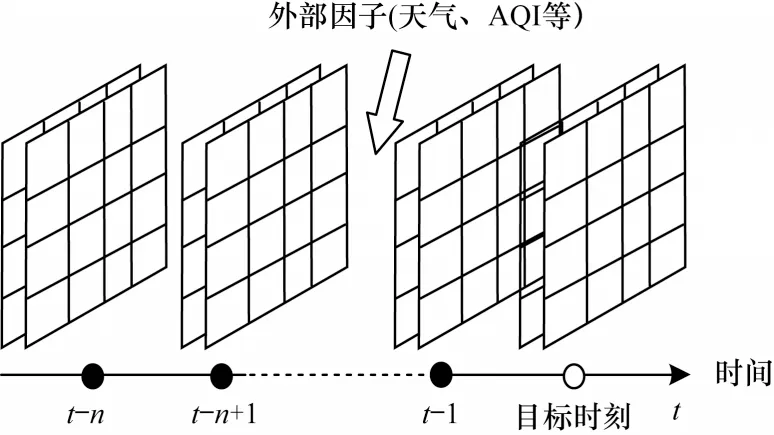
图1 预测问题定义Fig.1 Definition of the prediction problem

其中：Fprediction为预测问题；f为解决预测问题的混合深度学习模型；X为历史客流量输入；Ε为外部因子输入；W为可学习权重。

历史客流输入包括近邻、日周期和周周期模式的3 部分历史客流量数据，应用3 种不同周期的模式能够更好地研究地铁客流的周期性及周期时间片对目标时刻客流的影响，以达到更精准的预测。近邻模式表示最接近预测时刻的若干时间片数据，日周期和周周期模式与目标时刻处于相同时间片，但在日或周的周期循环中。如预测目标是周六上午7：00～7：10 的地铁网络中各站点的进出站客流量，那么近邻模式的输入就是最接近周六上午7：00 的若干时间片的客流量，日周期模式的输入是前N天每天上午7：00～7：10 的客流量，周周期模式的输入是前N周每周周六上午7：00～7：10 的客流量。3 种模式的输入可用式（2）表示：

其中：Xt表示第t个时间片的客流量数据，即目标时间片客流量；IC、ID和IW分别表示近邻、日周期和周周期模式的历史观测数据；IC、ID和IW中的时间片的数量分别是c、d和w；一天的时间片总数是n。

2 短时地铁客流预测模型

2.1 模型架构

地铁客流量是典型的时空数据，其时间特征表现在历史客流量对预测时间点客流量的影响，空间特征表现为前一站或前几站的客流量对当前站点的影响。因此，深度学习预测模型需考虑地铁客流量的时空属性。本文提出的混合深度学习模型简称ResGRUMetro，其结构如图2 所示。模型包括3 个部分，第1 部分用于捕获空间特征，将CNN 与残差单元（Residual Units，ResUnits）融合，构建ResNet，第2 部分主要利用GRU挖掘时间特征。此外，利用LSTM 耦合温度、空气质量等外部因子。作为第3部分改善模型预测的整体能力。最后利用参数矩阵融合的方式，将时空特征和外部特征融合输出，通过激活函数得到最终预测值。为更好地捕捉客流量的峰值，设计WSE 作为损失函数反向传播训练，加强对流量峰值的捕获。

图2 ResGRUMetro模型结构Fig.2 Structure of ResGRUMetro model

2.2 时空特征捕捉

CNN 是一类包含卷积计算且具有深度结构的神经网络，擅长处理具有类似于网格结构数据的神经网络，例如时间序列数据和图像数据，CNN 将其分别看作是在时间轴上经过有规律地采样形成的一维网络和二维像素网格。每个CNN 单层网络包括卷积、非线性变换、下采样3 个部分，每层的输入输出为一组向量构成的特征图，CNN 通过Kernel 系统逐层对输入信号完成映射，并对提取的特征进行非线性映射。最后，通过下采样阶段对前两步得到的特征信息进行采样。图3 是一个在二维向量上进行卷积运算的例子，图中仅处理全位于图像中的输入，由图3 可以说明输出张量是由输入张量通过卷积得到的。就地铁客流量而言，每个地铁站有由历史客流量组成的特征向量，为捕捉地铁站间的空间关联特征，将地铁网络数据转换为二维图像，水平轴表示时间，垂直轴代表地铁站，每个位置的值为历史地铁客流量，通过对图像执行卷积来进行预测。

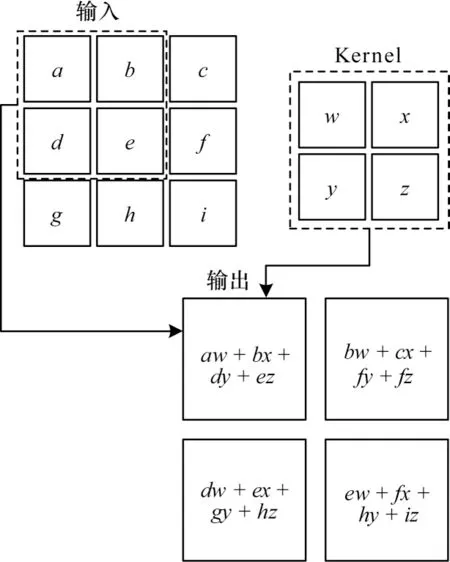
图3 卷积示例图Fig.3 Convolution example diagram

传统CNN 无法达到较深结构，随着隐藏层的增加，会出现梯度消失、网络退化、梯度爆炸等问题，损害模型的学习能力本文将残差结构融入到CNN 中，构建ResCNN 单元。一个典型的ResCNN 单元的结构如式（3）所示：

其中：XL为第L个残差单元的输入；XL+1为第（L+1）个残差单元的输出；Fr是残差函数。

残差结构的原理是学习关于XL的残差函数Fr，文中1 个ResCNN 单元由2 个堆叠的CNN 层和1 个捷径连接组成，如图4 所示。本文采用ReLU 作为残差结构中的激活函数，通过堆叠若干个ResCNN 单元，形成一个残差网络ResNet，以达到更深层的特征获取。

图4 ResCNN 单元结构Fig.4 Structure of ResCNN unit

为建模交通客流量在时间维度上的依赖，考虑利用RNN 的循环机制，但传统RNN 很难保持长期的依赖性，且存在梯度消失、梯度爆炸的问题［20］。LSTM 和GRU 是具有特殊结构的RNN，通过门控机制有针对性地保留信息，能够学习时间跨度相对较长的依赖关系，解决传统RNN 存在的问题。相较于LSTM，GRU 在保持LSTM 原有效果的前提下有更简单的结构和更快的学习速度，因此本文采用GRU捕获交通客流量的时间特征。GRU 的结构如图5 所示，1 个GRU 单元包含2 个门，即重置门和更新门，重置门用来丢弃与预测无关的历史信息，更新门用于控制历史状态信息对当前时刻的影响程度，更新门的值越大，状态信息保留越多。

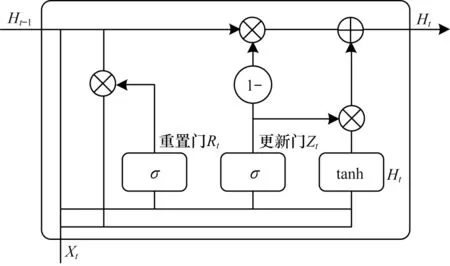
图5 GRU 单元结构Fig.5 Structure of the GRU unit

具体传播公式如式（4）所示：

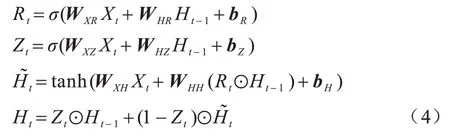
其中：Rt、Zt、和Ht分别为 重置门、更新门、当 前时刻的候选隐藏状态和隐藏状态；WXR、WXZ和WXH分别为输入层到重置门、更新门和隐藏状态的权重矩阵；WHR、WHZ和WHH分别为隐藏状态到重置门、更新门和另一隐藏状态的权重矩阵；bR、bZ、bH分别为更新门、重置门和候选隐藏状态的偏置向量；Ht-1为历史时刻的隐藏状态；Xt为当前时刻的原始输入；σ表示激活函数；⊙表示哈达玛积。

2.3 外部特征耦合

外部因素包括天气、重大事件、空气质量等影响人们的出行计划，进而对地铁客流量产生影响。例如，暴风雨天气会降低人们的出行欲望，节假日等重大事件会使城市交通迎来新的高峰，空气质量较差的日子人们大概率选择居家活动，这些外部因素潜移默化地影响人们的出行决策。目前，只有部分客流量预测模型引入了外部因素，且对空气质量的关注相对较少。本文选取的11 个外部指标可以分为3 类，包括天气状况（最高气温、最低气温、是否阴雨）、特殊事件（是否节假日）和空气质量（AQI、PM2.5、PM10、NΟ2、CΟ、Ο3、SΟ2浓度），利用LSTM网络对这些因子的时间序列进行分析，捕捉外部因子影响特征，优化模型预测精度。

由于3 个组成部分对预测结果的影响程度不同，本文采用参数矩阵方法对3 个部分进行融合。参数矩阵方法由ZHANG 等［21］提出，具体步骤为：

1）初始化参数矩阵，矩阵元素值范围为［0，1］；

2）各部分原始输出与矩阵做哈达玛积运算后相加融合；

3）通过迭代训练获得最小损失值的方式并确定最优权重。具体如式（5）所示：

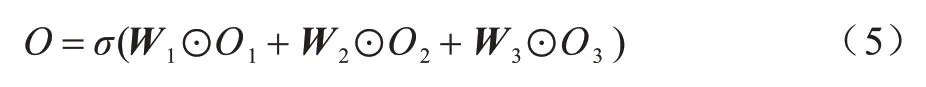
其中：Ο表示模型的最终输出；⊙表示哈达玛积；W1、W2和W3表示可学习权重；Ο1、Ο2和Ο3分别是模型前3 个部分的输出；σ是相应的激活函数。

2.4 训练损失优化

短时交通流量预测是一种典型的回归问题，研究人员普遍采用均方误差（Mean Square Error，MSE）作为训练的损失函数。MSE 是对所有样本预测值和真实值的方差取平均值，所有样本在计算误差时均会被附以相同的权重，它更侧重于误差的整体计量。然而在真实生活中，无论是对于出行者或是交通的管理者而言，都更加关注交通时序的峰值，以方便对出行时间进行合理规划及线路车次管理。MSE 采用算数平均的方式，难以有针对性地满足对于交通时序峰值的精准预测。为解决此问题，本文设计了一种面向短时交通流量时间序列预测的损失函数加权平方误差，使其更加关注对于交通流量序列峰值的预测误差，从而起到对损失函数进行优化的效果。WSE 的计算过程如式（6）所示：

WSE 在计算损失时根据交通流量的大小为预测误差赋予不同权重，加大了对交通流量时间序列峰值处误差的惩罚，这使得神经网络在反向传播时，会更加关注峰值处的预测和误差，最终在交通流量峰值处取得更为精确的预测。

3 实验结果与分析

3.1 数据集与评价指标

数据选自2015 年4 月上海市地铁进出站刷卡数据，共有289 个站点，覆盖全市14 条地铁线，平均每天有900 万条刷卡记录。据市民活动情况，本文选取6：40～23：00 为目标时间段进行客流量研究，以10 min 为时间切片，即每10 min 统计一次客流量，则30 天内共划分出2 940 个时间片。外部因子中的天气数据来自天气网数据，以h 为单位的空气质量数据来自中国环境监测总站提供的城市空气质量实时监测数据。训练数据来自4 月1 日～4 月23 日，验证数据来自4 月24 日和4 月25 日（含1 个工作日和1 个非工作日），测试数据来自4 月26 日～4 月30 日（含4 个工作日和1 个非工作日）。

为评估模型预测效果，选用平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、加权平均绝对百分比误差（Weighed Mean Absolute Percentage Error，WMAPE）进行量化分析，误差计算公式为：

3.2 实验环境与模型参数

本文实验在GPU 平台运行，运行环境为python3.6，利用python 的第三方库scikit-learn、Keras和TensorFlow 搭建交通流量预测模型。以10 min 为时间间隔统计流量数据，通过多次实验测试和调参，对模型的卷积核尺寸、CNN 神经元个数、残差单元个数、CRU 神经元个数进行讨论，结果如图6 所示。需说明的是由于MAE、WMAPE 指标波动较小，这里仅用RMSE 进行比较判断。最终模型的超参数设置：卷积核大小为3×3；3 层CNN 神经元个数均为128；残差单元个数分别均为16，2 层GRU 神经元的个数均为256，根据经验设置3 层LSTM 神经元，个数分别为256、128、64；输入数据周周期模式、日周期模式和近邻模式时间切片分别为7、1、1；在模型训练过程中，学习率为1×10-3，迭代次数为600 次，使用验证集早停策略以避免过拟合，采用Adam 优化器，损失函数为WSE。

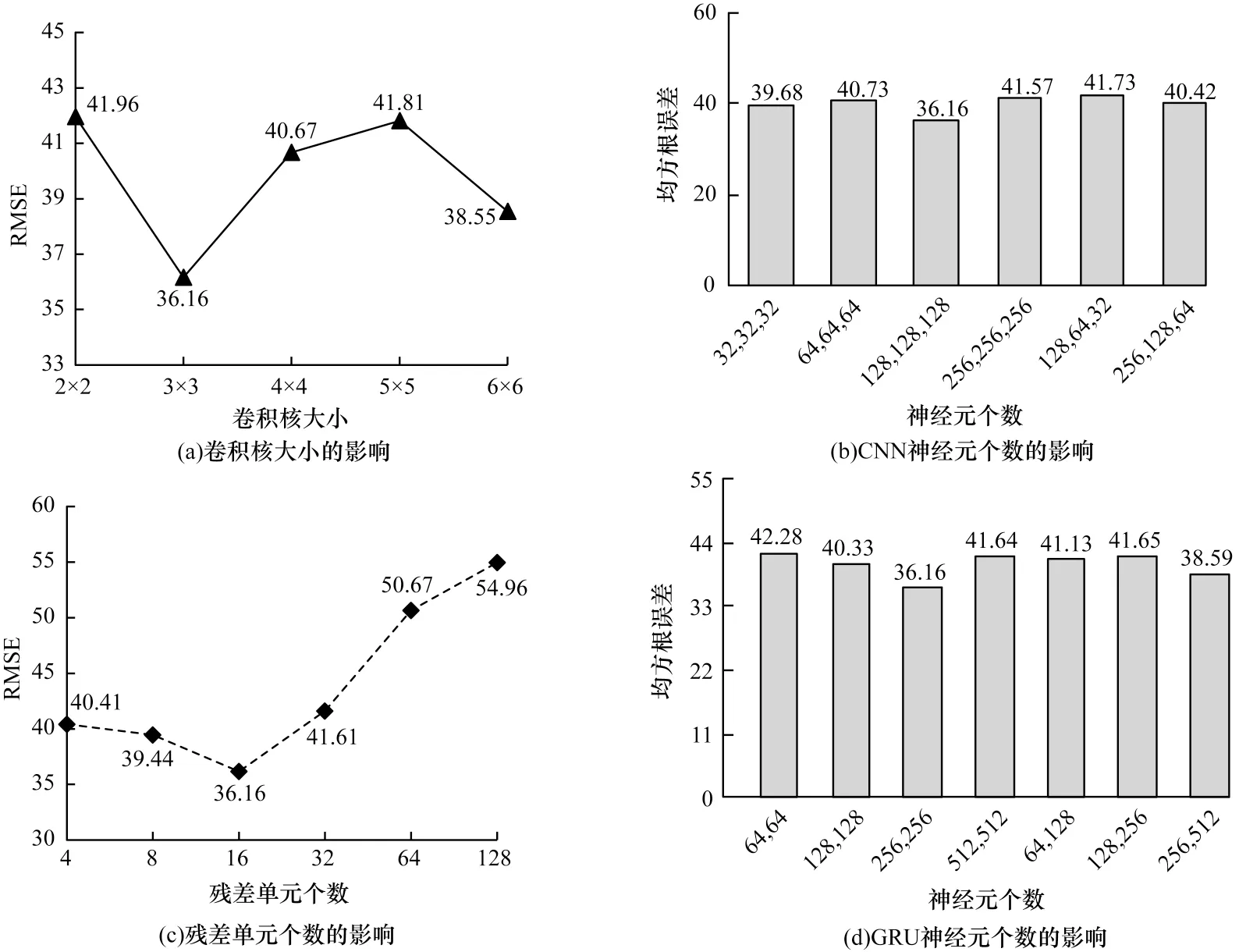
图6 本文模型的超参数调参Fig.6 Optimal hyperparameters of model in this paper

3.3 不同基准模型结果

分别以10 min、20 min 和30 min 为时间间隔进行流量统计，将本文提出的ResGRUMetro模型与已有经典模型进行比较，验证模型的预测性能。基准模型包括1 个统计学方法、1 个机器学习方法和4 个深度学习方法。

1）线性回归分析LR［22］：一种统计学方法，用于确定两种及以上变量间的依赖关系。

2）支持向量机PSVR［23］：一种机器学习方法，scikit-learn 核函数类型为“poly”。

3）卷积神经网络CNN［24］：一种深度学习方法。

4）ResNet：加入残差单元的卷积神经网络［21］。

5）门控循环单元GRU［25］，深度学习方法。

6）ResNet+GRU：ResGRUMetro模型除去天气因子和WSE 损失函数。

对比实验结果如表1 所示。

表1 地铁站客流量预测实验结果Table 1 Experiment results of passenger flow prediction for metro stations

由表1 可知，本文提出的ResGRUMetro模型在MAE、RMSE 和WMAPE 这3 种指标上较其他方法均取得了较优的结果。深度学习方法整体优于统计学方法和机器学习方法，考虑时空特征的深度学习方法结果优于仅考虑空间特征的深度学习方法。

以10 min 切片具体分析，相比LR 模型，ResGRUMetro模型 的MAE 相对减少了8.62%，RMSE相对减少了30.70%，WMAPE 相对减少了2.17 个百分点，这可能是因为LR 模型只能捕捉时间序列中的线性关系，对于非线性特征难以捕获。将ResGRUMetro模型与PSVR 对 比，ResGRUMetro的MAE相对减少了8.17%，RMSE 相对减少了24.43%，WMAPE 相对减少了2.20 个百分点，这说明ResGRUMetro在交通流量预测上的效果优于传统机器学习模型。与仅捕捉空间关联特征的CNN 和ResNet 对比，与仅捕捉时间关联特征的GRU 对比，ResGRUMetro均取得了较好的效果，这体现了时空混合模型的优越性。相比ResNet+GRU 模型，ResGRUMetro的MAE 相对减少了2.94%，RMSE 相 对减少了3.86%，WMAPE 相对减少了0.56 个百分点，表明引入天气因子以及改进的损失函数能提高模型预测能力。

3.4 模型峰值捕获能力

为直观展示ResGRUMetro模型捕获峰值的能力，本文讨论了在特定站点下不同时间片的进出流量预测情况。徐家汇是上海中央活动区之一，也是上海十大商业中心之一，日进出客流量较大，具有一定研究意义，因此选取徐家汇地铁站作为研究对象。

图7 是徐家汇站4 月26 日～4 月28 日（含1 个非工作日和2 个工作日）不同时间切片预测值与真实值的比较结果。由图7 可知，各时间切片ResGRUMetro模型预测结果与真实值拟合较好，且在峰值的捕获上有优越性。为进一步验证使用WSE作为损失函数对于ResGRUMetro捕获峰值特征的改进，选取以MSE 作为损失函数的ResGRUMSE模型作为基准模型，与以WSE 作为损失函数的模型ResGRUWSE进行对比实验。计算了所有站点的模型误 差，结果如表2 所示。由表2可知，ResGRUWSE模型的MAE 和RMSE 均优于ResGRUMSE模型，但WMAPE 稍有不足。以10 min 切片为例，与ResGRUMSE模型相 比，ResGRUWSE模型的MAE 相对减少了2.89%，RMSE 相对减少了3.13%，WMAPE 相对增加了0.28 个百分点。MAE 是衡量模型性能的最基本的方法，实验结果表明，在所有时间切片下ResGRUWSE模型均具有较低的MAE 值，表明其具备良好的预测性能。RMSE 可以放大模型中的较大偏差，RMSE 越小则证明ResGRUWSE模型的稳定性越好。但ResGRUWSE模型具有低MAE、低RMSE 与高WMAPE，表明预测误差可能主要来自流量数据中的低值，而不是来源于峰值。

表2 不同损失函数模型的预测实验结果Table 2 Experimental results of models with different loss function

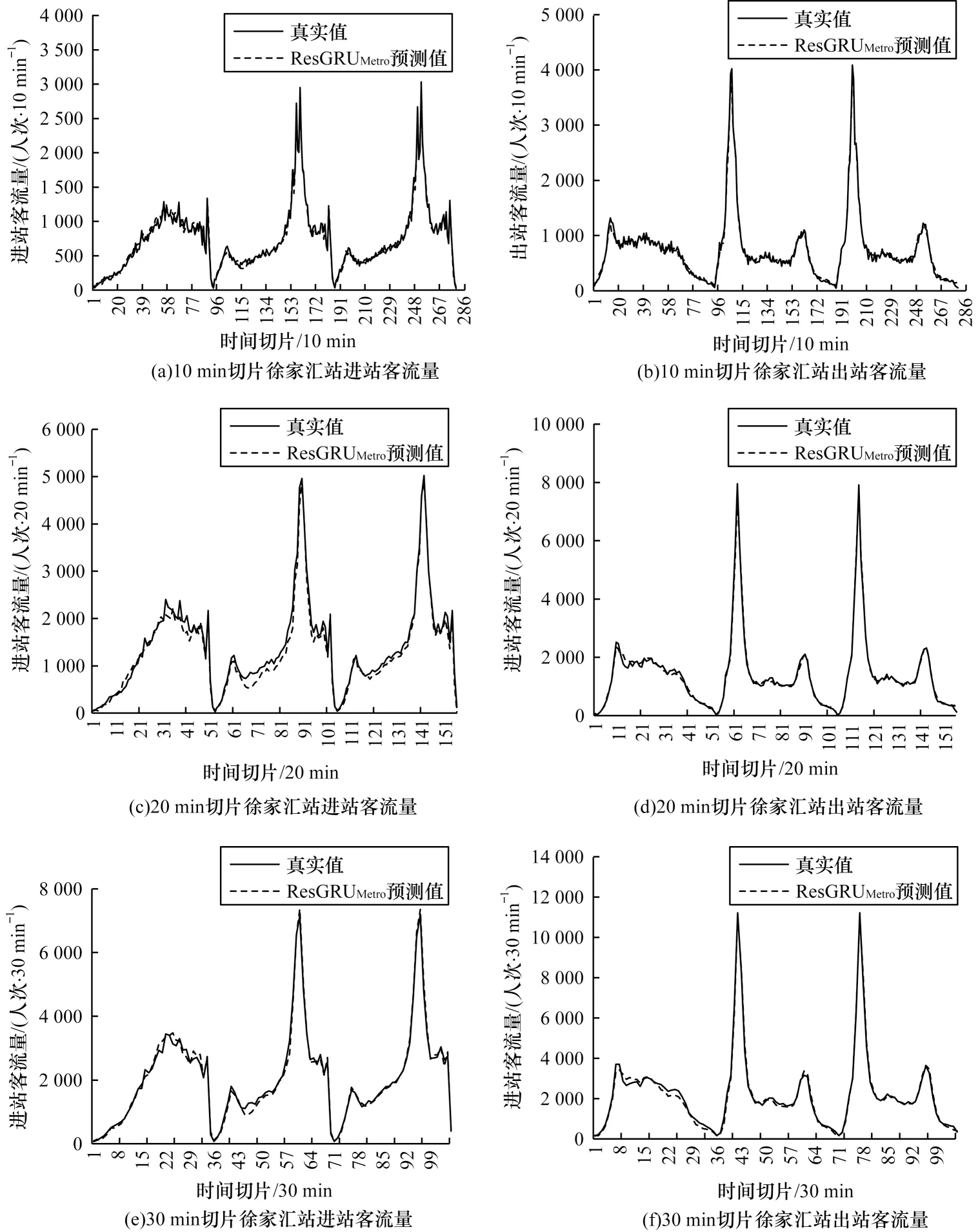
图7 在不同时间切片下徐家汇站进出客流预测结果Fig.7 Prediction results of passenger inflow and outflow for Xujiahui metro station in different time intervals

为进一步分析ResGRUMSE和ResGRUWSE模型在不同大小流量处的预测误差，将不同时间切片的流量数据分别划分为4 个流量阶段，分别对这4 个阶段绘制误差柱状图，如图8 所示。可以看出在流量高峰阶段，ResGRUWSE的表现明显优于ResGRUMSE，而流量低峰阶段ResGRUWSE的表现略差于ResGRUMSE，这可能是由于损失函数WSE 使模型更加关注流量序列中的峰值，从而在一定程度上弱化了对低值处的关注程度。在真实生活中，无论是对出行者亦或是交通的管理者而言，均更加关注交通流量时间序列的峰值，以方便出行时间的合理规划及车辆调度。虽然从总体上看，ResGRUWSE模型的WMAPE 并非最低，但是它具有较低的MAE 与RMSE，能够更精准地预测交通流量中的峰值，整体预测能力也较强。

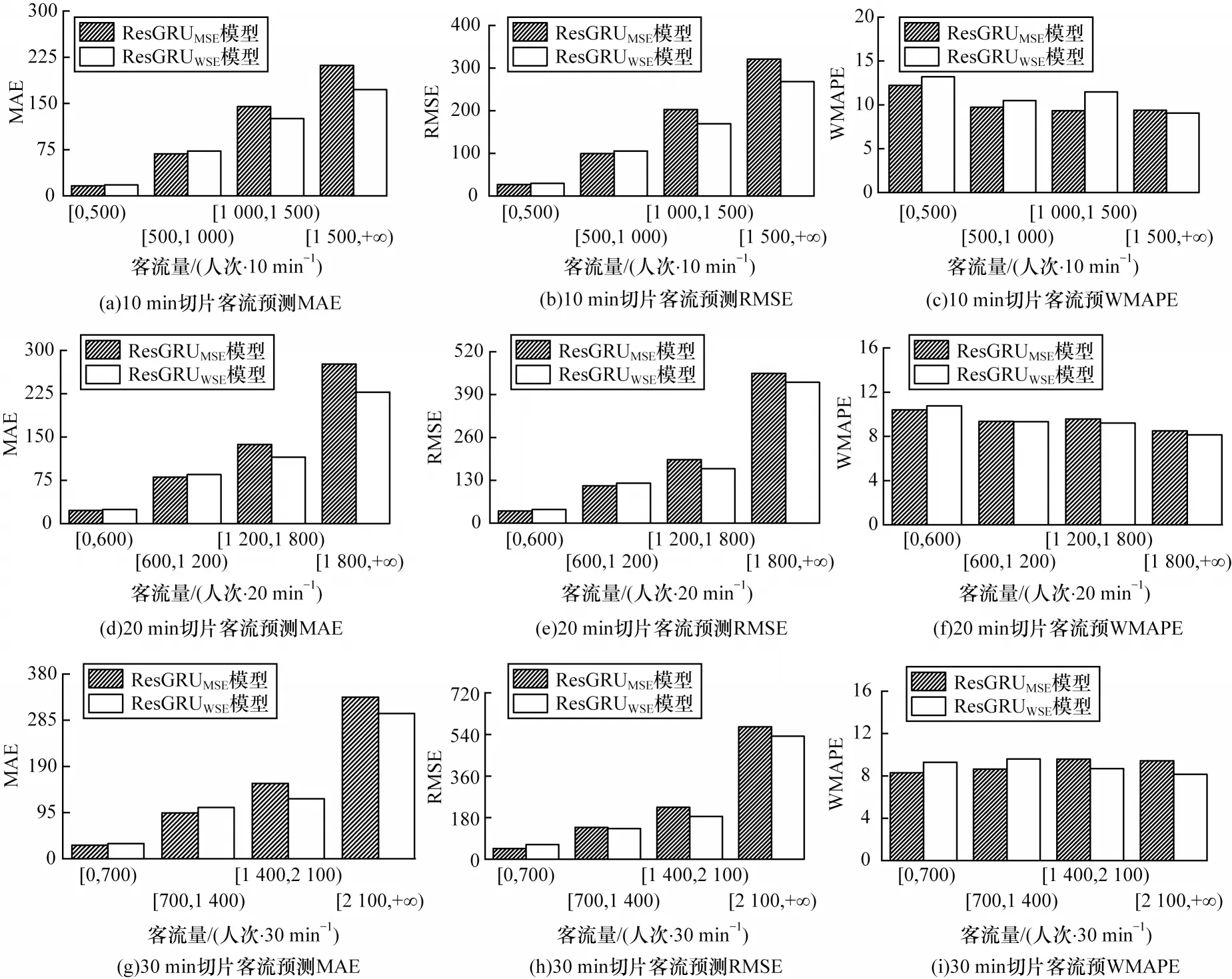
图8 不同流量阶段客流预测误差Fig.8 Prediction error of passenger flow in different flow stage

4 结束语

针对短时地铁客流量预测问题，本文从模型优化的角度出发，提出一种混合深度学习模型ResGRUMetro。将卷积神经网络与残差单元相结合，用于捕捉流量的空间特征，并利用门控循环单元捕捉流量的时间特征。为改进模型的预测能力，耦合天气、空气质量等外部因子，在模型训练上使用加权平方误差作为损失函数，提升模型流量峰值的预测能力。此外，探究ResGRUMetro模型在特定站点不同时间切片下的预测能力，对比以MSE 和WSE 作为损失函数的模型预测效果，并量化不同流量阶段的预测误差。实验结果表明，与LR、PSVR、CNN 等经典模型对比，ResGRUMetro具有较低的MAE、RMSE 和WMAPE 与较高的预测精度。下一步将寻找更长时间的交通流量序列对模型进行验证，并将混合模型应用于交通流量的多步预测问题中，以提高模型的鲁棒性。