六自由度机械臂运动学分析与仿真研究

何浪，谢明红，刘驰弋

（华侨大学机电及自动化学院，福建厦门 361021）

0引言

随着世界“工业4.0”进程的不断深化以及“中国制造2025”战略的全面部署，世界制造业的发展将日渐趋于数字化、网络化、智能化[1]。多自由度工业机械手臂在工业自动化领域中扮演着一个不可或缺的重要角色。在切割、焊接、喷涂、装配、码垛等多个工业领域有着非常广泛的应用，有效地降低了生产过程中的劳动力成本，提高了社会生产力，推动人类社会的工业自动化水平的发展。六自由度机械臂控制系统研究主要包括运动学分析和轨迹插补两部分核心内容，是机械臂精确、平稳、高效工作的重要保障。

传统的机械臂运动学控制系统的开发是基于机械臂物理实体设计过程，缺乏计算机软件的仿真模块，需要通过花费更多的时间力气调试机械臂，而且最终结果往往也不够准确[2]。当前随着计算机技术的飞速发展，各种仿真技术也被广泛应用到机械臂的控制系统研究当中，避免了直接在机械臂上调试，通过构建精度较高的机械臂模型，在仿真平台上模拟实现机械臂的实际运动情况，最后再通过对机械臂实体的调试，设计出更加精准、高效的机械臂控制系统。基于此，本文以钱江RH6型的六自度串联工业机器人为研究对象，通过对机械臂的运动学分析及轨迹规划的分析研究，在VS2017软件开发平台上，开发模拟机械臂运动过程的仿真软件。

1 运动学建模与求解

机械臂的运动分析采用的是由Denavit和Hartenberg在1955年提出的D-H参数法[3]。在机械臂的每个连杆上固连一个坐标系，以此来描述连杆在空间中的位置状态，通过齐次变换矩阵来描述各个坐标系之间的相对关系，从而来表示各连杆之间的相对位姿，在根据各连杆之间的位姿关系建立机械臂的运动学方程，求取机械臂的正逆解。

1.1 D-H模型构建

本文研究的钱江RH6型机械臂由6个转动关节串联而成。在对机械臂进行运动学分析之前需要对机械臂进行建模，确定每一个连杆上的坐标系。为了方便对连杆的描述，对各连杆进行标号，从固定基座开始为0号连杆，第一个可动连杆为1号连杆，直到机械臂的最末端连杆为6号连杆，连杆编号完毕开始确定连杆坐标系，连杆坐标系的建立需要遵循以下原则：1）按照笛卡尔坐标系的规则自由设定0号连杆的坐标系及其坐标原点位置；2）机械臂各关节均为转动关节，其连杆轴线由右手定则确定；3）将各连杆的上一个连杆的关节轴定义为该连杆坐标系的Z轴，Z轴方向可自由选定，通常平行的Z轴的方向相同；4）将相邻两连杆i轴和i+1轴的轴线的公法线设置为i轴连杆坐标系的X轴，X轴方向由i指向i+1，i轴和i+1轴的交点或公垂线与i轴的交点作为连杆坐标系的原点；5）各连杆坐标系的Y轴由右手定则确定。

机械臂的连杆坐标系建立完毕之后，需要确定各连杆的参数。连杆参数主要包括连杆夹角θi、连杆扭角αi、连杆长度ai、连杆偏距di。根据实验室机械臂的原始尺寸可以得到机械臂的D-H参数表，如表1所示。

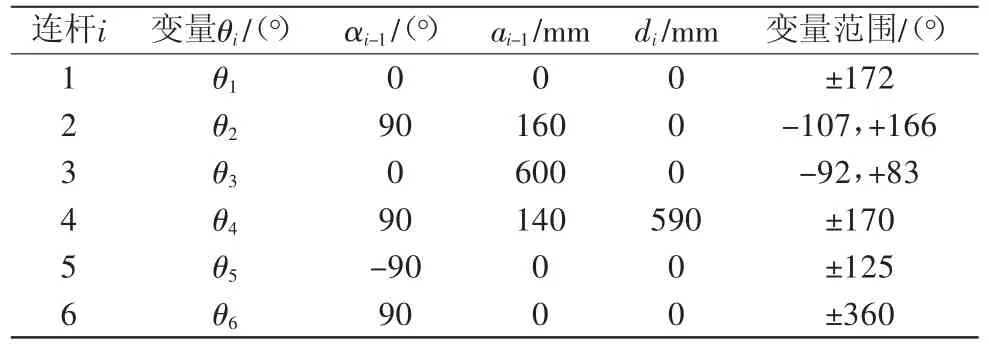
表1 钱江RH6型机械臂连杆参数表

建立机械臂的D-H模型如图1所示。

图1 钱江RH6型机械臂D-H模型

根据所定义的连杆坐标以及连杆参数，能够推导出相邻两关节坐标的矩阵变换关系为

1.2 正逆运动学分析

机械臂的正逆运动学分析主要包括正运动分析和逆运动学分析。正运动学分析是根据已知的各关节旋转角度来获取机械臂的末端位姿。逆运动学是根据机械臂的期望末端位姿反求各关节角的大小[4]。正运动学求解能够得到机械臂末端位姿的唯一解，而逆运动学求解既有可能得到多组封闭解，也有可能出现没有封闭解的情况。在应用过程中需要结合机械臂的实际应用场景及各关节转角限制约束来选取最优解。

机械臂的正运动学分析首先需要根据上文推导的相邻连杆坐标系的齐次变换矩阵及各连杆的参数来求解各相邻连杆之间坐标系的齐次变换矩阵。

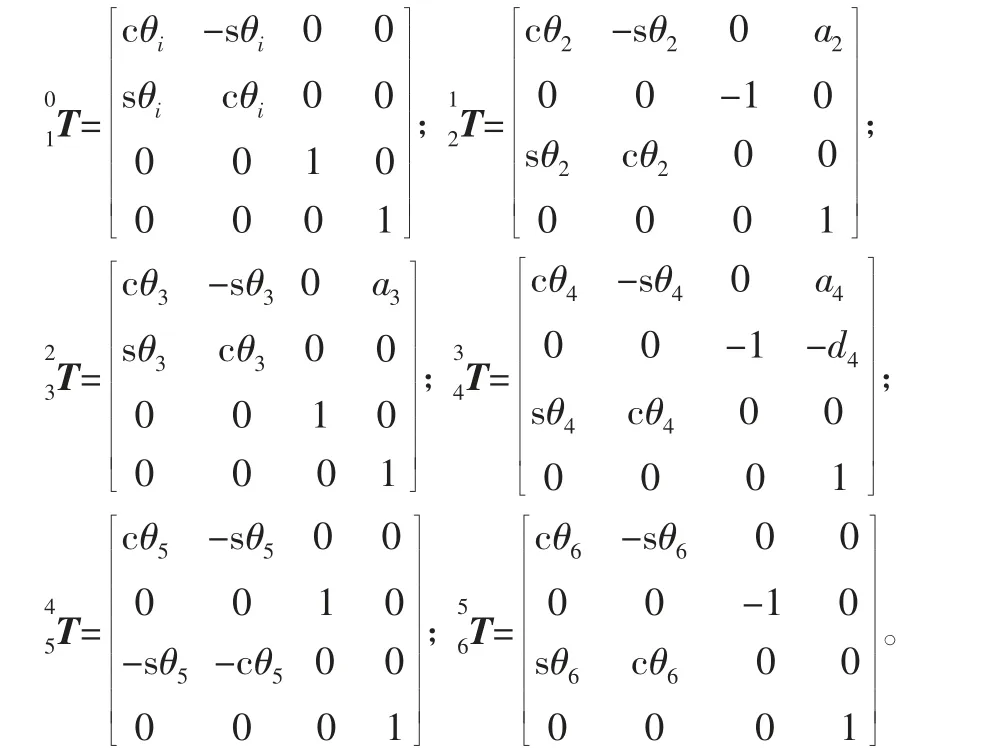
由上述各个连杆坐标之间的齐次变换矩阵,通过链式规则可以求解得到机械臂末端点和基座之间的齐次变换矩阵，即为机械臂的正运动唯一解：

式中：ci、si分别表示sin（i）、cos（i）；cij、sij分别表示sin（i+j）、cos（i+j）。

机械臂的逆运动学分析是通过给定机械臂的末端位姿来求解机械臂6个关节角的转动大小。由于本文所研究的钱江RH6型机械臂满足Piper原则，即机械臂的3个关节轴相交于一点存在着封闭解。因此，通过求解封闭解的方式来进行机械臂的逆运动求解分析。机械臂前3个关节角确定的是末端执行器的位置坐标，后3个关节角确定了末端执行器的姿态坐标，在逆解求解过程中先求解前3个位置关节角再求解后3个姿态关节角。

由上面的计算便可以求解出机械臂的前3个关节角，由计算结果可知θ1存在着两个解，对应的θ3存在着4个解，由于θ2能够由θ1和θ3唯一确定，所以前3个关节角总共存在4组解。最后，还需要确定出空间位置的最优解，根据机械臂各关节角的限制范围以及角度变化的原则可以获取机械臂空间位置的最优解。

根据所求得的θ1、θ2、θ3进一步求解机械臂的后3个关节角。在式（5）中，将等式两边的（1,3）和（3,3）元素对应相等，可以求解得到θ4的大小：

令式（14）两边元素（1,1）和（3,1）对应相等求解可得出θ6的大小：

通过上述求解，得到了机械臂的剩下3个关节角的大小。理论上，机械臂前3个关节角有4组不同的解，由于通过机械臂的腕关节的翻转可以获得同样的姿态，所以机械臂后3个关节角有2组不同的解。因此，机械臂理论上有8组不同的封闭解。根据机械臂各关节角的限制范围以及角度变化的原则可以从中选取出机械臂的最优解，来控制机械臂达到指定的目标位姿。

2 机械臂轨迹插补算法

插补算法是数控加工的指挥者，是机械臂控制系统的核心内容[5]。插补的过程就是根据NC代码离散成多段微线段的过程，常见的插补算法有空间直线插补算法和空间圆弧插补算法。插补算法按插补方式又有脉冲增量插补和数据采样插补。本文采用的是数据采样插补即时间分割法，将加工一段曲线的时间划分为若干个相等的插补周期，每经过一个插补周期就进行一次插补运算，计算出该插补周期内机械臂各轴的进给量。采用时间分隔法要求插补算法有较快的运算速度，能够在1 ms的插补周期内完成插补运算以及其他相关的运算及动作。因此，本文采用常见的空间直线和圆弧插补算法来实现机械臂的轨迹插补，插补周期设置为1 ms，每个插补周期的插补步长Δl由插补周期和进给确定。

2.1 空间直线插补

直线插补是根据已知直线轨迹的终点坐标，分解出在每个插补周期各个轴的运动分量，如图2所示。

图2 直线插补

假设直线轨迹的终点坐标为pe（xe，ye，ze），首先需要确定当前插补周期的起点坐标。当当前加工直线轨迹为第一个程序段，那么将坐标原点设置为起点。否则，我们将上一段加工轨迹的终点设置为起点，将所确定的起点坐标定义为po（xo，yo，zo），可以求出直线轨迹的总长度l：

当直线轨迹插补到最后一个插补周期时，剩下的直线长度llast≤Δl时，将最后一个插补周期的步长设置为Δlδ=llast，再分别投影到各个坐标轴上，可以得到各轴的进给量。最后直到直线余量llast=0时，完成直线插补过程。

2.2 空间圆弧插补

空间圆弧插补是将NC代码所确定的圆弧轨迹离散为多段微线段。在空间坐标系中，确定一段圆弧轨迹需要3个点，在NC代码中给出的是圆弧的起点坐标、终点坐标及圆弧轨迹的圆心坐标。假设圆弧轨迹的终点坐标为pe（xe，ye，ze），圆心坐标为po（xo，yo，zo），首先确定圆弧轨迹的起点坐标，若当前加工直线轨迹为第一个程序段，那么将坐标原点设置为起点。否则，我们将上一段加工轨迹的终点设置为起点，将所确定的起点坐标定义为ps（xs，ys，zs）。

根据已知的条件可以求得以下内容：

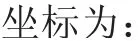
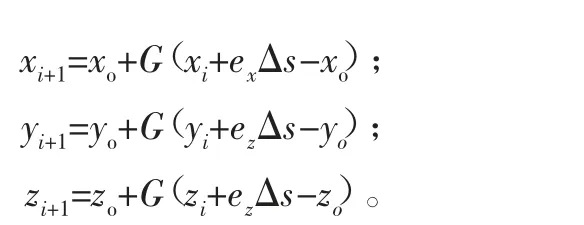
当剩余圆心角θδ小于步距角Δθ时，圆弧插补进入到最后一个插补周期，此时令步距角等于剩余圆心角，计算出各轴进给量。当θδ=0时，圆弧插补结束。

六自由度机械臂不仅仅是计算机械臂空间位置的插补，还需要考虑机械臂空间姿态的插补。在本文采用的是均匀变化的方式进行姿态插补，假设起点姿态为ps（αs，βs，γs），终点姿态为pe（αe，βe，γe），那么可以得到每个插补点pi的姿态公式为：

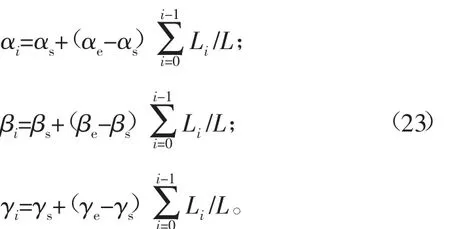
根据上面的直线与圆弧的插补算法，可以求得各个插补周期中插补点的空间位姿pi（xi，yi，zi，αi，βi，γi），通过逆运动学分析，将笛卡尔坐标系下插补点的空间位姿求逆解得到关节坐标系下各轴的转动角度pi′（θi1，θi2，θi3，θi4，θi5，θi6）,通过关节坐标系下各轴的角度来模拟仿真机械臂的运动过程。

3 OpenGL仿真软件开发

在机械臂的控制系统研究过程中，仿真环节是必不可少的一环，通过对机械臂的运动过程的仿真能够模拟出机械臂末端执行器的实际运行轨迹，验证运动学算法及插补算法的准确性。本文采用的是基于MFC窗口框架下的OpenGL来进行机械臂的实时仿真。OpenGL是一种纯软件的图形库函数，不受硬件条件和不同操作系统的限制，支持多种语言开发，能够为图形软件开发提供非常丰富的图形API接口函数。本文的OpenGL仿真软件开发的主要流程包括三维建模和仿真实现两部分。在调用OpenGL库函数前，需要在基于MFC框架中配置OpenGL的开发环境。在VS2017的软件开发平台中已经集成了OpenGL32.lib库函数，再通过导入glut32.lib即可完成OpenGL开发环境的配置。

3.1 三维建模

三维建模主要包括机械臂的运动轨迹建模和机械臂的实体建模两部分内容。机械臂的运动轨迹模型的建立是通过解析NC代码获取加工图形每一工步的顶点坐标，将其存储到数组当中，根据G01、G02、G03分别区分加工轨迹的直线、顺圆、逆圆。直线轨迹的绘制直接通过调用OpenGL中的直线绘制函数glBegin（GL_LINES）和glEnd（）。圆弧轨迹的绘制需要对圆弧进行离散，离散结果是许多微线段，当线段数量足够多的时候，轨迹便能够无限逼近圆弧，将这些离散出来的点根据直线绘制的方式绘制出来便能够实现圆弧轨迹的建模。图4是NC代码马单环的轨迹建模效果图。

图4 马单环轨迹模型仿真

机械臂实体建模首先需要通过三维软件分别画出机械臂6个连杆的实体模型，将其保存为obj格式，obj文件是通过点的坐标来描述三维模型，在obj文件中主要由关键字及点位坐标组成，在通过obj文件导入三维模型的过程中需要先解析obj文件，提取不同关键字下的数据将它们分别保存到数组中，然后再通过调用OpenGL中的三角形绘制函数glBegin（GL_TRIANGLES）和glEnd（）来绘制模型的各个三角面，最后组合成机械臂的3D模型。

完成了机械臂的实体建模之后还需要实现其动态仿真过程，机械臂的动态仿真过程其实质就是图形的几何变换问题，可以通过调用OpenGL 库函数中的函数glTranslatef（x，y，z）来实现机械臂模型在X、Y、Z方向的平移动作，调用函数glRotatef（Angle_x，1，0，0）、glRotatef（Angle_y，0，1，0）、glRotatef（Angle_z，0，0，1）来分别实现机械臂绕基座标系的X、Y、Z轴的转动，调用函数glScalef（m_xScalse, m_yScalse, m_zScalse）可以实现机械臂模型的放大和缩小动作。

3.2 仿真实现

建立了机械臂的三维模型并实现了机械臂的动态仿真的模拟，接下来便可以进一步完成机械臂的仿真软件的开发。机械臂在工业领域的实际应用中主要有点动和联动两种运动方式，对应在仿真软件中需要分别模拟出机械臂的点动控制和联动控制。点动控制的实现是通过给定机械臂各关节需要转动的关节角，通过运动学求正解算法确定机械臂末端执行器的位姿，同时在仿真软件界面上实时显示机械臂末端执行器的位姿。联动控制是控制机械臂的六轴联动到达指定的目标位置，从而实现目标轨迹的运动。

软件客户端指定机械臂的NC代码，仿真软件需要读取并解析指定的NC代码，通过直线和圆弧插补算法将NC代码离散成许多间隔很小的点，通过机械臂逆运动学求出各轴的关节角，将它们保存到自定义的数组中实时传递给OpenGL的旋转函数，并且在软件界面实时显示机械臂末端执行器的动态位姿，从而实现对机械臂按照目标轨迹的动态仿真。

4 结语

本文通过对钱江RH6型机械臂的运动学分析和插补算法的研究，采用OpenGL模拟仿真了机械臂在实际加工过程中的运动情况，开发了一套基于MFC的六自由度机械臂仿真软件。软件能够实现机械臂的实时点动控制和联动控制两种不同的运动模式，实时跟踪机械臂末端执行器的运动轨迹及各轴的旋转角度，能够较好地实现机械臂动作过程的模拟仿真，对后期在机械臂上的实操作业有非常重大的指导意义。