落石撞击桥墩计算模型研究现状与展望

2022-05-14唐剑明卢思吉

广东公路交通 2022年2期

李宇，汪洋，唐剑明，卢思吉

(四川省公路规划勘察设计研究院有限公司，成都 610041)

0 引言

随着交通建设的发展，山区高速公路的建设取得长足进步。由于地形条件限制，桥梁占比大，且其中有很大一部分位于不良地质区，灾害风险较高。落石是山区道路、桥梁的主要灾害之一，近年来落石撞桥事故时有发生，如2009年7月，一块重达130t、约50m3的巨石从大约500m的高度滚落撞击都汶公路彻底关大桥[1]8#桥墩，导致第8和第9跨桥梁倒塌；2020年9月，G5京昆高速公路雅西段发生山体崩塌，导致姚河坝大桥[2]右幅两孔坍塌并阻断桥下国道108线；2020年10月，由于山体岩石崩塌，国道245线K808+600处宝水溪二号桥梁板严重受损(图1)。落石撞击桥梁造成车辆被砸、桥梁局部破损甚至坍塌、阻断交通，严重危及行人及车辆安全，同时造成很大的经济损失，落石清理、桥梁修复工程量大、工期长，造成不良的社会影响，是亟待解决的问题。

图1 典型落石撞桥事故

目前针对桥梁撞击的研究主要集中于船撞桥和车撞桥，《公路桥梁抗撞设计规范》(JTG/T3360-02-2020)仅给出了船撞桥的计算理论，对落石撞桥并未给出相应的指导意见。相比于落石撞击桥面，落石撞击桥墩的事故更为常见，也是引起桥梁倒塌的主要原因之一。为此，国内外学者对落石撞击桥墩进行了一系列研究。本文拟从落石撞击力的静力计算方法、简化动力计算方法和桥墩损伤特征及影响因素等方面对落石撞击桥墩的研究现状与发展进行总结与分析，为工程设计及进一步研究提供参考。

1 落石撞击力静力计算方法

等效静力计算方法是将撞击体产生的撞击力视为外荷载，直接施加于结构上，进行静力计算。目前，落石撞击桥墩的理论撞击力大多采用Hertz弹性碰撞理论，该理论最早由Hertz于1881年提出用于分析弹性球体受压接触面之间的接触应力。如图2所示，假定两球在压力P作用下接触面为半径为a的圆，图中δ=δ1+δ2为总压缩量，两球弹性碰撞力为：

(1)

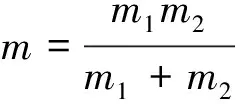
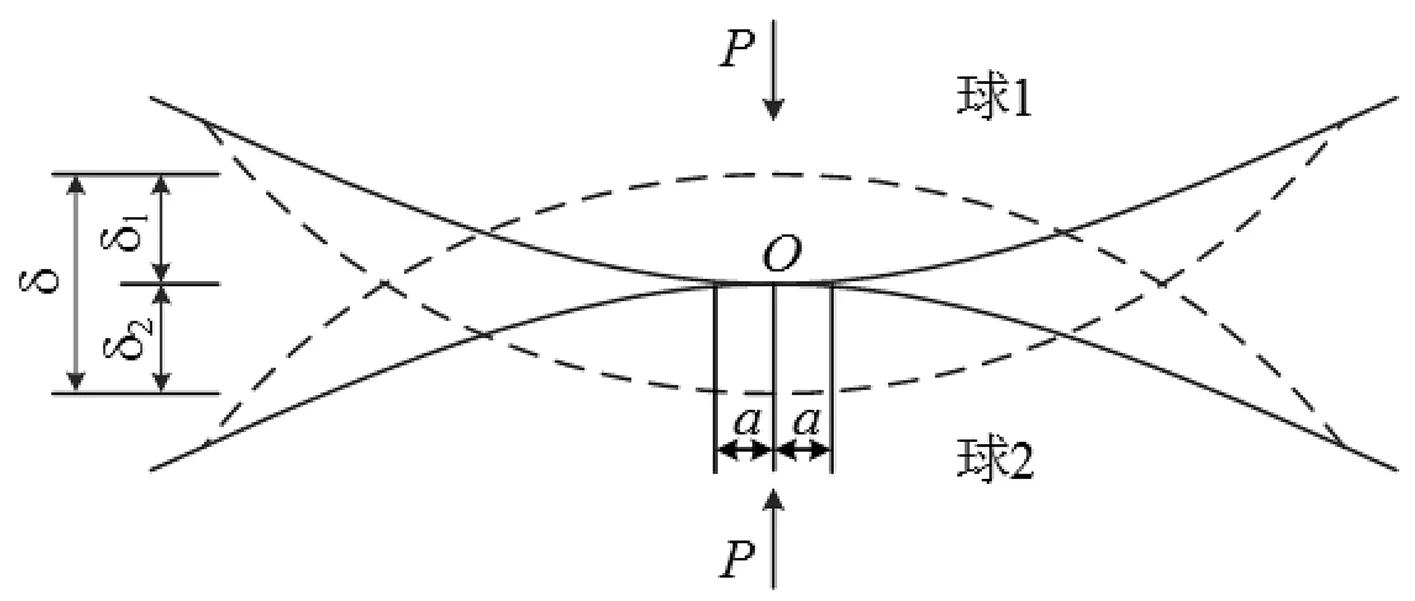
图2 Hertz弹性碰撞模型

该理论以材料处于线弹性为基本假定，在撞击速度较小时是适用的，但是当撞击速度较大时，接触面上产生塑性变形，往往高估撞击力，偏差随着撞击速度增大而愈加明显。

陈剑[3]等以Hertz接触理论和Thornton弹塑性假设为基础，将材料视为理想弹塑性，塑性区接触压应力不变，通过引入材料弹塑性修正系数，修正了泥石流中大块石对桥梁撞击力大小的计算公式。结果表明，材料修正系数在0.20～0.45之间，其值与材料屈服强度成正比，与冲击系统的等效模量E呈反相关关系；该式计算的撞击力随着撞击速度增大而增加缓慢，撞击力明显小于hertz理论所得的值，结果相对合理。

基于Hertz理论及Thornton弹塑性假设的碰撞力修正公式存在修正曲线适用性未得到充分验证的不足，更为重要的是该方法主要采用了球体之间的碰撞力公式，实际上桥墩多为圆柱体或长方体，有必要推导典型桥墩几何形状与球体的碰撞力解析解，并以此为基础考虑弹塑性及系数修正。

目前各国规范结合碰撞理论和试验研究提出了一系列落石撞击力的计算公式，包括《公路路基设计规范》(JTJ13-95) 公式、隧道手册公式、日本道路协会公式、瑞士公式、澳大利亚公式等。

(1)《公路路基设计规范》(JTJ13-95)公式。路基规范给出了根据石块质量计算的崩塌体撞击力公式：

(2)

式中：F为撞击力(N)；Z为石块冲击陷入被撞物的深度(m)；Q为石块的重量(N)；γ为缓冲填土的重度(N/m3)；φ为缓冲填土的内摩擦角；A为石块等效球体的面积(m2)；v为石块撞击速度(m/s)。

式中A可表示为:

(3)

(2)隧道手册公式。《铁路工程设计技术手册-隧道》中给出撞击力的近似计算方法：

(4)

式中：冲击持续时间近似按压缩波考虑，时间可按Δt=2h/C计算，其中h为缓冲回填土厚度，C为压缩波在缓冲层内的往复速度，计算公式：

(5)

式中：ρ为缓冲层密度(kg/m3)；E为弹性模量(Pa)；μ为泊松比。

(3)日本道路协会公式。日本道路协会[4]基于Hertz弹性碰撞理论，假定落石为刚性球、砂垫层为平面，建立落石冲击砂垫层最大撞击力公式：

(6)

式中：λ为垫层的拉梅常数(Pa)，建议取值106Pa，实际值根据垫层密度的不同在106～107之间变化；H为滚石下落高度(m)。

(4)瑞士公式。Labiouse等[5]通过上铺土垫层钢筋混凝土板的滚石冲击试验和基于Hertz碰撞理论原理，建立了滚石最大撞击力经验计算公式，可表示为：

(7)

式中：Er为垫层反应模量(Pa)。

(5)澳大利亚公式。Pichler等[6]模拟落石对砂砾土质垫层的冲击，得到撞击力计算公式：

(8)

除了上述规范中提出的落石撞击力计算公式，一些学者通过试验和数值模拟也提出了不同的落石撞击力静力计算方法。

杨其新[7]等通过重锤自由下落到土槽的试验，提出了落石撞击棚洞撞击力计算公式：

(9)

式中：a为冲击过程中的加速度(m/s2)。

袁进科[8]通过滚石冲击试验拟合得到撞击力放大系数，提出了基于隧道手册的撞击力改进公式(式10)，式中θ为入射角度；η为恢复系数。

该公式计算的落石对桥墩的撞击力与数值模拟结果相近[9]，是目前用于计算落石撞击桥墩较为典型的公式。

(10)

以上公式均考虑了缓冲层的影响，但理论依据及计算参数不尽相同，计算结果差异较大。根据罗征[10]等的比较分析，以冲量定理为基础的公路路基设计规范公式计算值小于撞击力荷载峰值，计算结果偏小；基于半经验半理论的日本道路协会公式和瑞士公式计算值与试验撞击力峰值更接近。王星[11]等认为澳大利亚公式和杨其新公式则整体上略有偏小，这主要是由于这两种算法都是基于动量定理及现场试验得出的。值得一提的是，上述公式计算的撞击力与落石撞击桥墩的撞击力实验值仍有一些差距[10]。

此外，部分学者还通过数值模拟或试验研究了落石速度、质量、撞击位置、重力效应等因素对撞击力的影响。例如，李兴民[12]等通过数值模拟研究了滚石撞击桥墩撞击力与滚石速度与质量的关系，结果表明：如果设计目标确定为滚石撞击时桥墩不发生大面积的塑性破坏，则撞击力与撞击速度、撞击质量之间为线弹性关系；当撞击质量和撞击速度均较大时，桥墩被撞击部位进入塑性，撞击力不再随撞击速度和质量的增加而线性增加，撞击力的增加速率显著减小。袁进科[9]等采用数值模拟方法模拟了彻底关大桥在落石冲击作用下的损毁过程，提取的撞击力时程显示整个撞击事件持续时间约为0.3 s，撞击力在很短的时间内到达峰值，并快速衰减，但是模型未考虑混凝土中钢筋的影响，破坏模式与实际破坏模式存在一定的差异。何思明[1]等进一步考虑了纵筋及箍筋和结构自重的影响，数值模拟结果显示撞击力持续时间约0.05 s，考虑重力效应的冲击载荷峰值较不考虑重力效应时约大9%,可见，落石撞桥持续时间短暂，重力效应对撞击力影响较大。Sun[13]等通过摆锤撞击试验分析得出摆锤下落高度相同时，桥墩上撞击位置越高，峰值撞击力越小，衰减时间越长，但是并未给出撞击力计算公式。

2 落石撞击力简化动力计算方法

落石撞击桥墩简化动力分析模型主要有单质点弹簧动力系统、两自由度质量弹簧动力系统等两种。

简化外力模型不能考虑撞击体质量的影响，不能反映撞击接触过程。采用质点弹簧动力系统(图3)，即采用非线性弹簧模拟撞击体与被撞体之间的相互作用，能够避免上述不足。该方法的关键是获得撞深-撞击力关系曲线，目前关于船的撞深-撞击力关系曲线研究较多[14-15]，而针对落石的撞深-撞击力关系曲线研究还比较少。

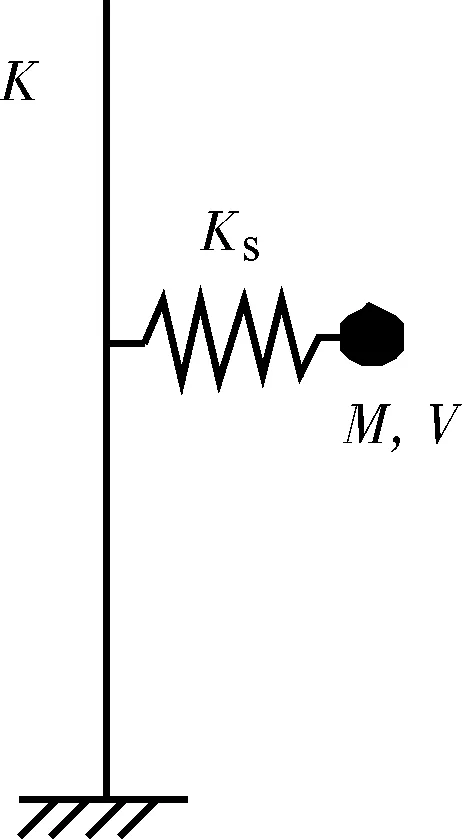
图3 单质点弹簧动力模型

该模型能够明显提高计算效率，但也存在以下不足：模型中桥墩刚度采用以静力荷载下位移相等为原则的等效刚度，模型适用于桥墩等效刚度大的情况，当桥墩等效刚度较小时，相同动力荷载下的响应差异明显[16]。该模型只适用于正撞情况，无法考虑撞击角度变化的影响，也无法考虑撞击体外形的影响。

两自由度质量弹簧阻尼系统(图4)是动力相互作用分析常用的模型，已在桥梁振动分析及减振方面得到广泛应用。2009年，Fujikake[17]等将该模型用于分析梁的冲击破坏，通过与试验结果比较，证实了该模型用于分析钢筋混凝土梁整体弯曲破坏模拟的有效性。之后，樊伟[18]等进一步证实了该模型对受压UHPC墩柱冲击破坏也具有较好的预测效果，同时提出采用弹塑性梁单元计算抗力曲线。

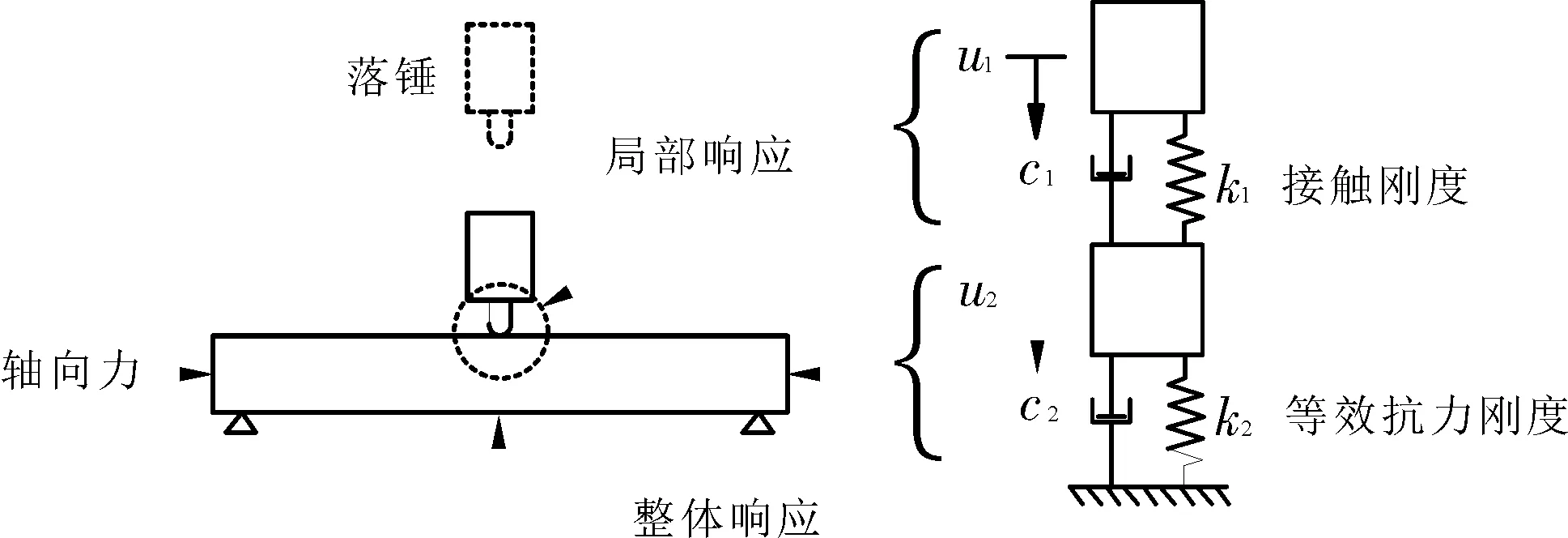
图4 两自由度质量弹簧动力模型

3 落石撞击桥墩破坏特征及影响因素

不同材料的桥墩抗落石撞击性能存在差异，其抗撞性能影响因素也不同。针对常用的钢筋混凝土桥墩、纤维混凝土桥墩及钢管混凝土桥墩分析其落石撞击破坏特征，并分析各自的抗撞性能影响因素。

3.1 钢筋混凝土桥墩

Liu[19]等通过落锤冲击实验研究了不同轴压下钢筋混凝土圆柱在冲击荷载下的行为，并比较了配筋率的影响。结果表明：圆柱破坏模式为以弯曲破坏为主的弯剪破坏，接触区及支撑区出现局部损伤，锤柱接触面及支撑位置墩柱下表面出现混凝土剥落，如图5所示。高能量冲击情况下，P-Delta效应对承受轴力的墩柱影响显著。

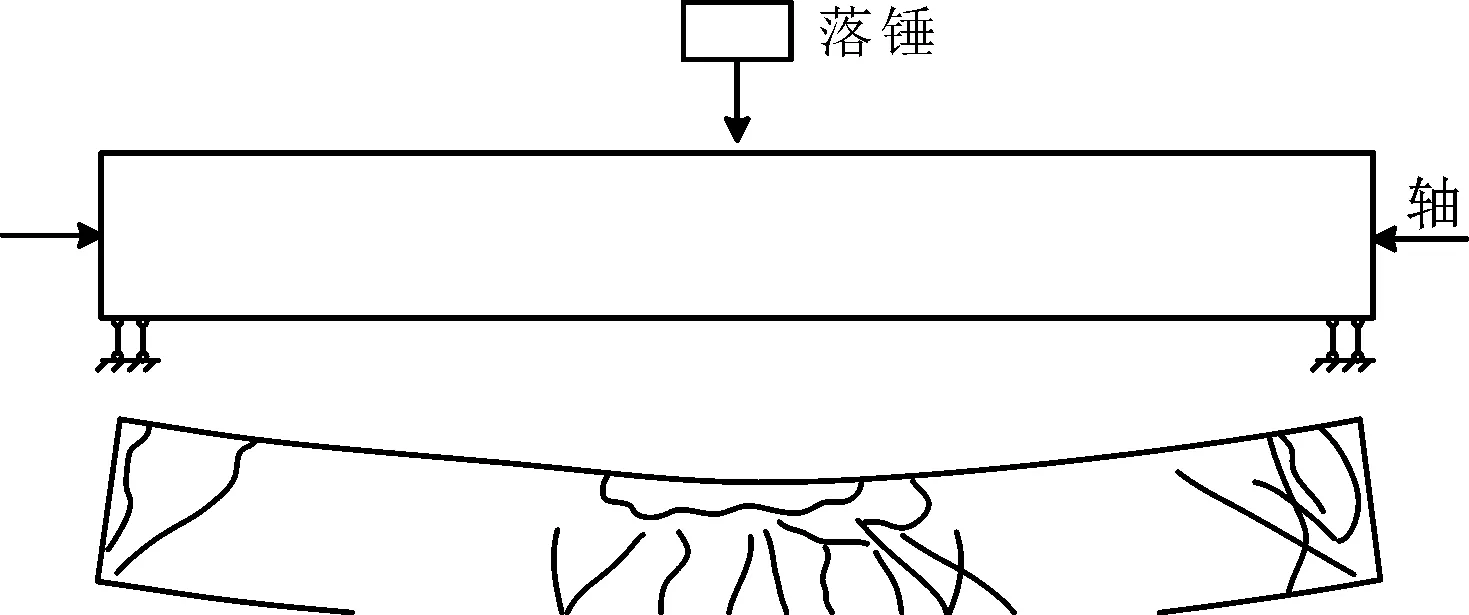
图5 落锤侧向撞击墩柱试验墩柱典型破坏模式[23]

罗征[10]等通过钢筋混凝土矩形悬臂墩摆锤撞击试验得出，撞击荷载作用下墩柱撞击区域出现剪切裂缝的同时，墩底也会出现弯曲裂缝(图6)，冲击响应过程可分为脉冲阶段及缓冲阶段。脉冲阶段的墩柱冲击响应振幅高、持时短，墩柱趋于直剪破坏；缓冲阶段的墩柱冲击幅值低，但持时短，墩柱趋于弯曲破坏。

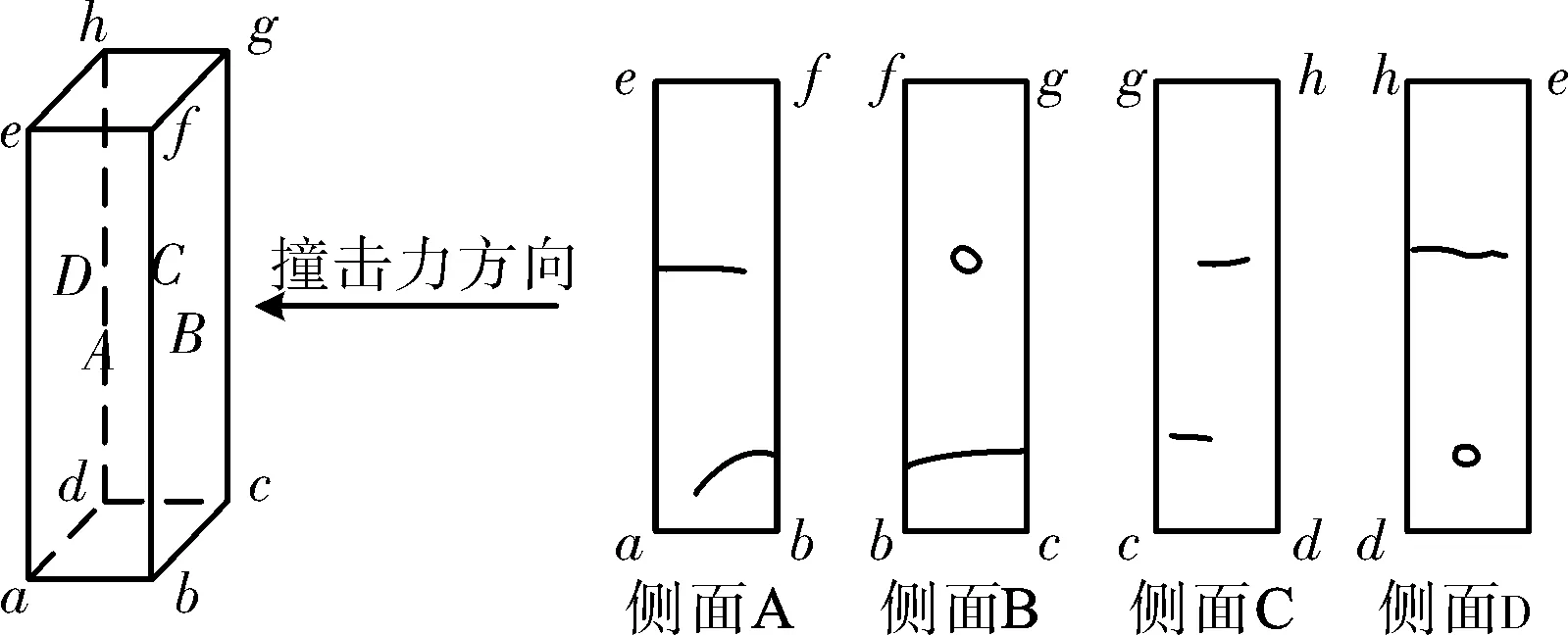
图6 摆锤撞击墩柱试验墩柱破坏特征

Sun[13]等通过摆球试验研究了桥墩在滚石撞击下的响应及损伤。墩柱在摆球冲击下的破坏模式为弯剪破坏，剪力引起撞击点处贯通裂缝，弯矩引起墩底裂缝。相关文献研究认为：轴压比小于0.3时轴力对桥墩施加了约束，从而提高了墩柱抗撞能力，当轴压比大于0.6时轴力会减小抗撞能力。Xie[20]等对钢筋混凝土墩柱的落石撞击数值模拟得出上部结构自重能够提高墩柱的抗撞性能。

余志祥[21]等通过数值模拟比较了落石冲击高度、冲击速度、水平冲击角度和落石直径等对桥墩损伤的影响。结果表明：在高能量冲击作用下，落石直径和冲击速度对墩柱破坏影响相对较大。顾乡[22]等采用数值模拟方法研究了落石冲击的高度、速度、偏心距、冲击角度、冲击面以及直径因素对墩柱的损伤破坏程度的影响，得到上述相似结论。

3.2 纤维混凝土桥墩

樊伟[18]等进行了掺加纤维UHPC墩柱和普通钢筋混凝土墩柱的落锤多次冲击试验。试验发现UHPC柱整体破坏形式为弯曲破坏，普通混凝土墩柱为弯曲变形导致的轴向压溃。采用UHPC后墩柱的抗冲击性能显著提高，相同配筋率和轴压时，受压UHPC柱所能承受的抗冲击能量约为普通混凝土柱的2.27倍。同时，提高配筋率和配箍率可有效地提高墩柱的抗冲击性能，相比无轴力的UHPC柱，受压UHPC墩柱的抗冲击性能显著提高。

3.3 钢管混凝土桥墩

王潇宇[23]等进行的钢管混凝土柱水平横向冲击试验结果表明：一端固支、一端简支的钢管混凝土柱易发生受剪破坏，而悬臂柱则发生根部弯曲破坏。钢管混凝土桥墩抗撞能力主要与轴压比[24]、温度[25]、套箍系数等相关。

康昌敏[24]等进行的数值模拟结果表明：当轴压小于0.7时，轴力对钢管混凝土的抗撞击性能有提高作用；当轴压比大于0.7时，轴力对钢管混凝土的抗冲击性能有削弱作用。史艳莉[25]等通过钢管混凝土构件在火灾与撞击联合作用下的数值计算，结果表明：随着温度升高，构件的抗撞击性能逐渐降低，当温度超过400℃后，构件抗撞击性能损失严重。

朱翔[26]等进行的钢筋混凝土墩柱抗冲击试验结果表明：在其他条件都一致的前提下，外包钢管加固RC柱在抗冲击高度为4.5m时未破坏，而RC柱在冲击高度为1m时即发生了破坏，表明外包钢管加固 RC柱的抗冲击性能得到了较大提高。