基于修正反应谱高墩连续刚构桥地震响应研究

肖龙, 冯仲仁, 陈百奔, 王雄江

(武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070)

中国抗震规范JTG/T B02-01—2008《公路桥梁抗震设计细则》设计加速度反应谱是通过对823条水平强震记录统计分析得到的[1]，桥梁在进行抗震计算时并未考虑长周期地震动因素的影响。柔性体系桥梁一般自振周期较长，频率较小，而在长周期地震动作用下，地震动能量低频成分显著，场地的卓越周期较长，当桥梁的自振周期与场地卓越周期较接近时，易产生“双共振”现象。因此，对应于加速度反应谱下降段，此时结构会产生较大的动力响应[2]。中国对于自振周期较长的柔性桥梁一般采用时程分析法进行抗震计算，但是王君杰、范立础[3]认为，反应谱法对柔性桥梁的抗震设计仍然具有较大价值，以考虑结构恒载初始几何刚度作为地震分析的初始状态，所得出的线性和非线性结果比较接近；并且统计得到的反应谱不取决于强震记录样本的随机性，具有较好的适用性。在长周期地震动作用下，考虑到柔性桥梁结构会产生较大地震响应时，地震反应谱长周期段取值会影响抗震计算的结果，从而直接影响地震响应的预测结果。因此，考虑长周期地震动的因素对规范加速度反应谱长周期段进行修正是必要的。

1 规范反应谱的缺陷

以JTG/T B02-01—2008《公路桥梁抗震设计细则》为例，经无量纲化后的规范水平设计加速度反应谱计算公式[1]如式(1)所示，阻尼比为0.05。

(1)

式中：Smax为加速度反应谱峰值；T为桥梁结构的自振周期；Tg为场地的特征周期。

根据结构动力学方程以及忽略小阻尼比的影响，有以下关系式：

PSV=PSA/ω

(2)

SD=PSA/ω2

(3)

式中：ω为自振周期对应的频率；PSV、SD、PSA分别为拟速度反应谱、相对位移反应谱和拟加速度反应谱。

对于大跨桥梁等柔性结构，在进行抗震设计时需要用到相对位移反应谱，并以此作为抗震设计的重要依据[4]。因此，在对规范反应谱修正时，相对位移反应谱的客观真实性就显得十分重要。

该文取规范Ⅰ类场地(Tg=0.35 s)设计加速度反应谱，并从美国太平洋地震工程研究中心(PEER)地震波库中选择2条对应Ⅰ类场地的PJH315和CFH000地震动加速度反应谱，将以上3条加速度反应谱曲线分别进行无量纲化处理，按式(3)分别计算得到无量纲化的相对位移反应谱，如图1所示。

图1 规范、PJH315和CFH000无量纲化相对位移反应谱

从图1可以发现：2条实际地震动记录的相对位移反应谱谱值刚开始随自振周期增加有增长的趋势，但在达到某一特定周期(达到峰值)后，谱值随自振周期逐渐减小，而规范相对位移反应谱随着自振周期的增加而线性递增[5-6]。规范和实际地震动记录的相对位移反应谱在长周期段增减趋势差异显著，规范相对位移反应谱出现明显的失真现象[7]。

2 考虑长周期地震动的修正反应谱

2.1 反应谱修正的地震动记录选取

目前，对于长周期地震动的界定标准尚未明确，有关学者[8]提出界定长周期地震动的方法是，在[2 s,10 s]内功率谱密度与[0 s,10 s]内功率谱密度面积之比a≥30%，通过筛选和分析验证了该界定方法较为准确。在选取长周期地震动记录时，该文借鉴此方法。

根据中国场地类别划分原则，有关学者统计了长周期地震动在4类场地发生的数量及占比，Ⅰ、Ⅱ、Ⅲ、Ⅳ类场地长周期地震动的占比分别为3.1%、2.5%、6.3%、8.3%[9]。从数据中发现，长周期出现在Ⅲ、Ⅳ类场地的概率明显大于出现在Ⅰ、Ⅱ类场地的概率，意味着长周期地震动更易出现在软弱土层。吕红山、赵凤新等[10-11]对适用于中国场地类型，地震动记录按照PEER中对应的以地下30 m处土层的剪切波速Vs30为标准进行分类。按照此原则从PEER中选取了4种场地地震动记录共612条，根据已有记录的长周期地震动发生概率，确定选取的长周期地震动数量及占比如表1所示。

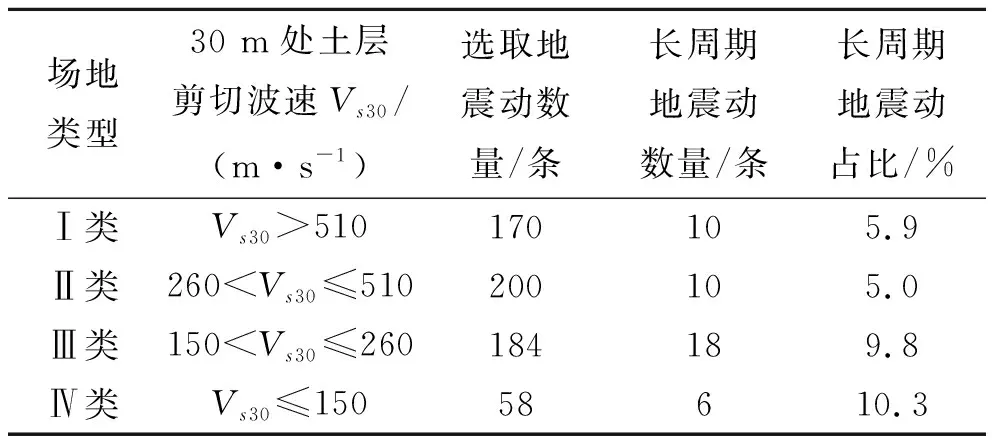
表1 各类场地下选取地震动记录数量、长周期地震动记录数量及占比

2.2 修正加速度反应谱

基于王君杰、范立础[3]等修正的加速度反应谱并针对规范反应谱的缺陷，该文提出加速度反应谱在长周期段衰减指数随自振周期呈多段线性变化，并确定了修正反应谱的相关参数，拟合修正后的无量纲化加速度反应谱计算公式如式(4)所示：

(4)

式中：T1、T2、T3为反应谱临界周期(s)，且T3=T2+ΔT，ΔT为地震动样本参数统计的周期间隔；k1、k2为衰减指数且k1=0.7+0.2(T-Tg)/(T1-Tg)，k2=0.9+0.1(T-T1)/(T2-T1)；ρs为地面运动最大位移值与加速度反应谱峰值之比；ρd为位移反应谱峰值与地面运动最大位移值之比；其他参数意义同前。

修正后的加速度反应谱与式(1)对比可知：修正加速度反应谱前两段与规范反应谱相同，现将规范长周期段的衰减规律修正为T-k衰减，其中衰减指数k包含k1、k2随周期线性变化，通过谱值统计确定公式中参数T2、ΔT、ρd、ρs等，且由已统计的参数计算确定临界周期T2[12]，最后根据T3=T2+ΔT即可求得T3。该文通过参数统计和特征拟合，得出修正加速度反应谱计算公式[13]。

2.3 修正加速度反应谱公式参数确定

(1) 衰减指数k1、k2的确定

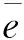
(5)

(6)

当衰减指数在[0.7，1.0]分别取不同值时，在[Tg，2.5 s]范围内采用式(5)、(6)计算所得的相关性系数和平均误差如表2所示。从表2得出：随着衰减指数的增大，相关性系数r逐渐减小，即相关性逐渐变差，而平均相对误差却逐渐减小。由于在[Tg，T2]内加速度反应谱斜率和衰减速度逐渐减小，该文将衰减指数k从定常数修正为在[Tg，T2]的分段线性函数，以0.9作为长周期前两段衰减指数分段线性函数的临界点，即衰减指数k1=0.7+0.2(T-Tg)/(T1-Tg)，k2=0.9+0.1(T-T1)/(T2-T1)。

表2 在[Tg，2.5 s]不同衰减指数下修正加速度谱和平均加速度谱相关性计算结果

(2) 确定反应谱长周期特性参数ρd、ρs和ΔT

地震动反应谱长周期特性参数ρd、ρs和ΔT，应结合加速度反应谱和相对位移反应谱来确定。该文通过统计4类场地的612条地震动，按式(7)、(8)计算其长周期特性参数ρd、ρs和ΔT并进行平均[3]，给出长周期特性参数合理建议值，如表3所示。

表3 地震动反应谱长周期特性参数的平均值及建议值

(7)

(8)

(3) 计算T2和T3

若使修正的相对位移反应谱在临界周期T2处达到峰值，则有如下关系式[3]：

(9)

由式(4)可求得T2的计算公式为：

(10)

修正的相对位移反应谱在T2处达到峰值经过ΔT才结束峰值平台到达T3，则T3为：

T3=T2+ΔT

(11)

将已统计的参数代入式(10)、(11)中，即可求得T2和T3，如表4所示。

表4 经统计计算的T2、T3值

2.4 规范反应谱、修正反应谱和所选取地震动的平均反应谱比较

根据地震动平均反应谱的统计规律和考虑修正反应谱的包络原则，该文对抗震规范的特征周期进行合理修正[14]，将规范中Ⅰ、Ⅱ、Ⅲ、Ⅳ类场地的第3组场地特征周期Tg分别修正为0.55、0.60、0.70、0.75 s。根据修正后的加速度反应谱公式及式(2)、(3)，计算4类场地在修正后特征周期Tg下的反应谱，再与地震动平均反应谱进行比较。限于篇幅，该文仅列Ⅲ类场地下反应谱比较图，如图2所示。

从图2(a)可知，加速度平均反应谱、修正加速度反应谱在谱值上的接近程度比规范反应谱更好，考虑特征周期修正后，修正加速度反应谱包络效果较好；从图2(b)可知，修正速度反应谱谱值在长周期段随自振周期而递减，与地震动速度平均反应谱统计规律吻合，而规范速度反应谱谱值在长周期段却为定值；在图2(c)中，修正位移反应谱在长周期段有明显的平台，紧接着谱值随周期而逐渐衰减，与地震动位移平均反应谱统计规律吻合，而规范位移反应谱谱值一直随周期线性递增。因此，从图2可知：在Ⅲ类场地下，修正反应谱能较好地反映地震动平均反应谱的统计规律，修正效果良好。

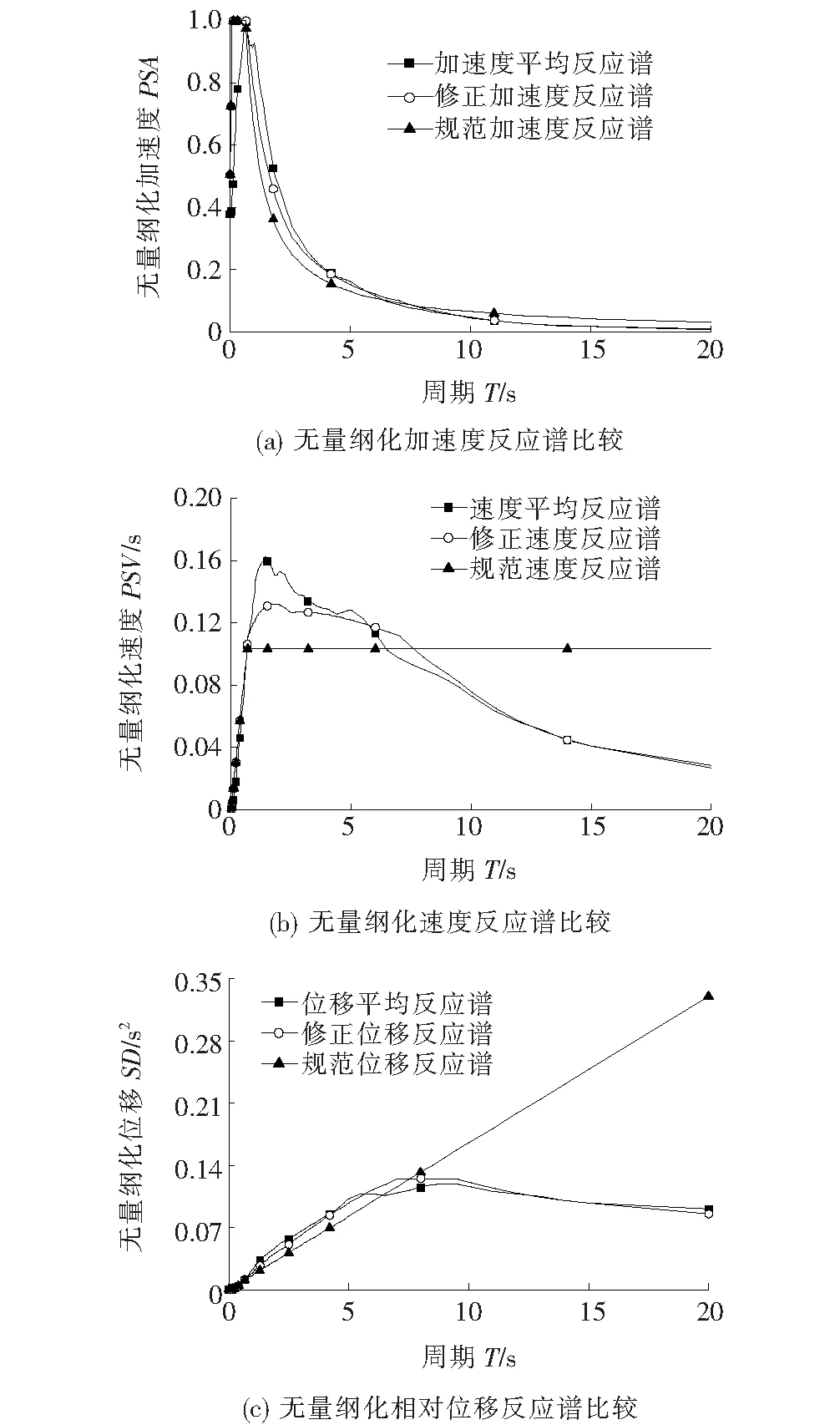
图2 Ⅲ类场地下地震动平均反应谱、规范反应谱和修正反应谱比较

3 有限元分析验证

3.1 工程概况

为研究长周期地震动对长周期桥梁结构地震响应和抗震设计的影响，该文以中国西南地区某桥跨布置为(82.5+150+82.5) m高墩预应力混凝土连续刚构箱梁桥为工程依托，对修正反应谱进行有限元分析验证。桥梁总长315 m，桥面宽7 m，主墩高73 m，设计汽车荷载等级为公路-Ⅱ级，抗震设防烈度为8度，抗震设防类别为B类，地震动反应谱分区特征周期为0.45 s，工程场地类别为Ⅲ类。桥梁上部箱梁采用C55混凝土，单箱单室截面，梁高及底板厚从根部到跨中采用1.8次抛物线变化。下部构造主墩采用C40混凝土，为矩形实心双肢薄壁墩形式，墩高73 m，双薄壁墩净距6 m。主墩承台和桩基均采用C30混凝土，承台厚4.5 m，基础采用桩径为2.5 m的钻孔灌注桩，每墩共9根桩，均为嵌岩桩。桥梁立面图和关键截面布置如图3所示。

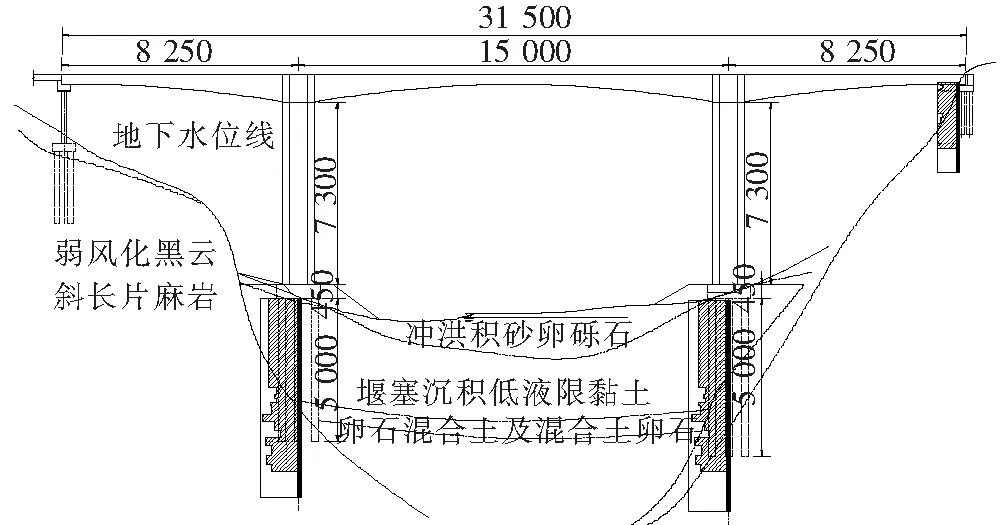
图3 桥梁立面和关键截面布置图(单位：cm)

3.2 有限元模型建立

采用CSiBridge软件建立高墩连续刚构桥动力分析有限元模型，主梁、主墩和桩基均采用空间框架单元模拟，主墩承台采用板单元模拟，全桥共665个节点，557个框架单元，48个板单元。该桥为高墩连续刚构桥，自振周期较长，长周期特性明显，考虑地基土和桩基的桩土作用效应，模型在桩基不同深度处施加水平正交的等代土弹簧来模拟地基土刚度，等代土弹簧的刚度采用“m法”计算。考虑到在地震等瞬间荷载作用下土抗力比持续荷载作用大，一般取m动=(2～3)m静[15]，该文取m动=3m静。主梁边支点设置纵向活动支座，采用约束横桥向和竖桥向，释放纵桥向约束的连接单元模拟，主梁与双薄壁墩采用全约束的连接单元模拟，桩底采用添加全约束的节点支座模拟。钢筋和二期恒载采用在单元上附加质量模拟，建立的有限元模型如图4所示。

超前探水是在隧道掘进之前采用钻探设备对隧道将掘进段地质情况和岩层渗水涌水情况进行全面了解，为治水方案的选择奠定基础。

图4 全桥动力分析CSiBridge有限元模型

3.3 动力特性分析

模态分析是动力特性分析的基础，根据JTG/T B02-01—2008《公路桥梁抗震设计细则》，当桥梁采用多振型反应谱法进行地震效应计算时，所考虑的模态阶数在计算方向上获得至少90%的有效质量[1]。该文采用Ritz向量法求出桥梁前500阶模态，在第491阶模态，得到X、Y、Z3个方向的累计振型参与质量分别达到了95.08%、94.55%和99.85%，说明模型提取的前500阶模态已经达到规范要求，可进行后续的反应谱分析。限于篇幅，仅列出该桥的前10阶模态和自振特性，并描述其相应的模态形状，如表5所示。

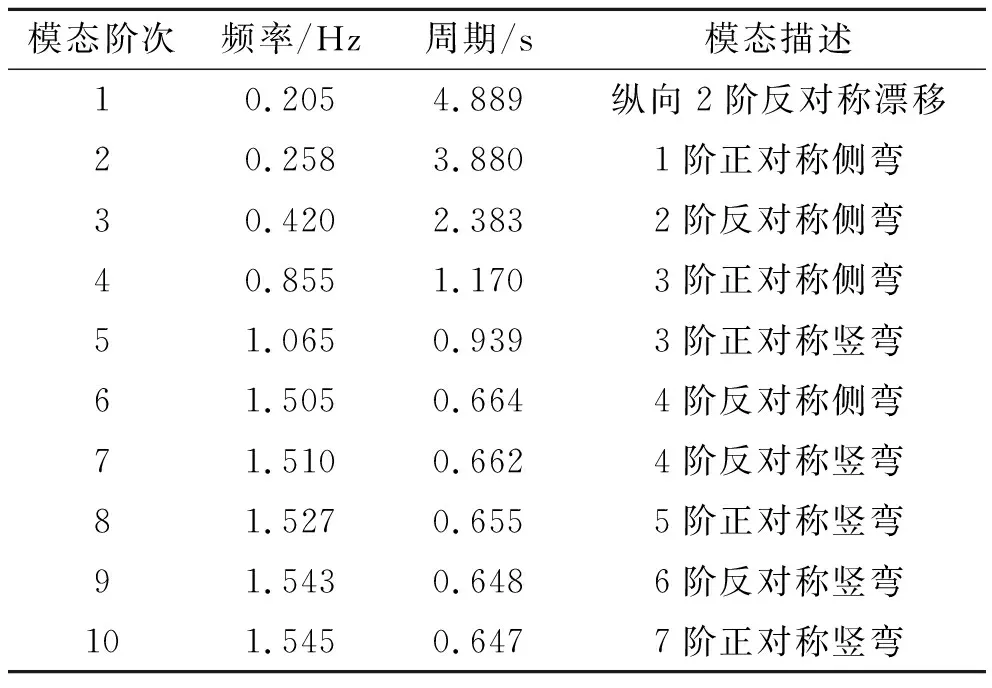
表5 桥梁前10阶自振频率和振动模态特性

从表5可以得出：桥梁的基频为0.205 Hz，自振周期为4.889 s，前10阶模态形状主要表现为主梁纵向反对称漂移、桥梁横向侧弯和竖弯振动，且桥梁各阶振动模态单一而不相互耦合。在第1阶振动模态主梁出现纵向2阶反对称漂移，主墩反对称纵向弯曲振动，表明该桥顺桥向刚度比横桥向弱。

3.4 反应谱分析

该桥的桥梁分类为B类，抗震设防烈度为8度，水平向设计加速度峰值A为0.2g，区划图的特征周期为0.45 s，场地类型为Ⅲ类，桥梁阻尼比取0.05。该桥主跨150 m，墩高73 m，属于非规则桥梁，在反应谱分析时可采用多振型反应谱法，根据文献[1]，反应谱计算相关参数如表6所示。

表6 反应谱计算相关参数

考虑3个正交方向(水平向X、Y和竖向Z)的地震作用，采用CQC法将各阶模态计算结果进行组合[16]。竖向加速度反应谱根据规范中谱比函数R乘以水平加速度反应谱得到[1]。该文考虑三向地震作用，采用荷载工况：纵桥向(X)+0.3横桥向(Y)+0.5竖向(Z)。地震动采用纵∶横∶竖=1∶1∶0.5模式输入，计算在E2地震作用下桥梁关键截面的内力和位移响应[17]，规范和修正加速度反应谱如图5所示。

图5 E2地震作用下规范加速度反应谱和修正加速度反应谱

3.5 时程分析

桥梁所在场地为Ⅲ类，该文从PEER地震波库中选取3条普通地震动ELC270、COD270和DLT352，3条长周期地震动ILA004-W、ILA056-N和CHY116-N来进行地震时程分析。经计算发现：普通地震动DLT352和长周期地震动CHY116-N产生的桥梁内力和位移响应均比其他同组地震波的大，则取其作为时程分析计算的地震波。在E2地震下，DLT352和CHY116-N地震波有效加速度峰值分别为0.350g、0.052g，对原始地震波进行调幅[18]，峰值调整系数分别为0.966和1.500，其加速度时程曲线如图6所示。荷载工况和地震动输入模式与反应谱分析时保持相同，将地震动输入模型进行时程分析。

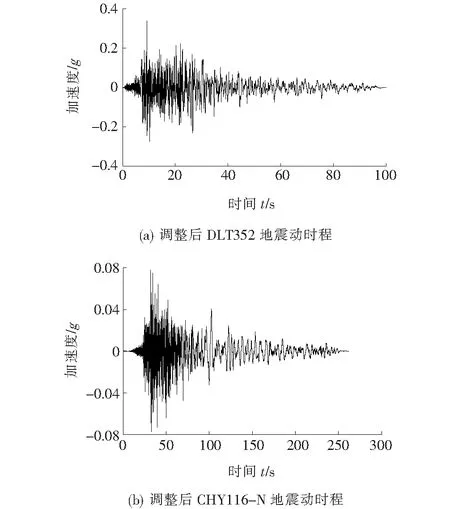
图6 E2地震作用下调整后的DLT352和CHY116-N加速度时程

3.6 反应谱和时程分析结构响应结果对比

在E2地震作用下，分别对结构进行反应谱分析和时程分析，得出桥梁在规范反应谱、修正反应谱、普通地震动和长周期地震动下的位移和内力响应，分别如图7～10所示。

图7 E2地震作用下X方向位移

图8 E2地震作用下Y方向位移

图9 E2地震作用下Z方向位移

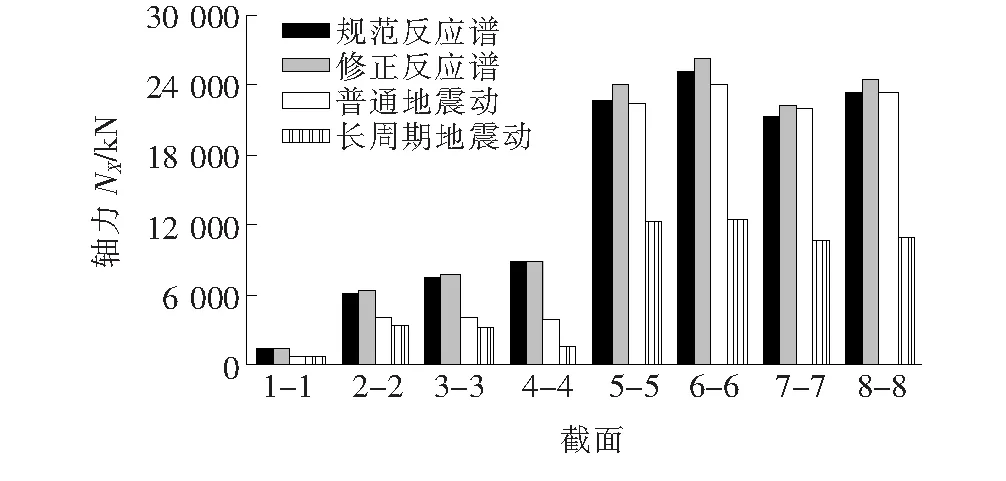
(a) 轴力NX

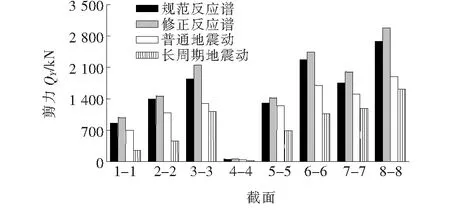
(b) 剪力QY

(c) 剪力QZ

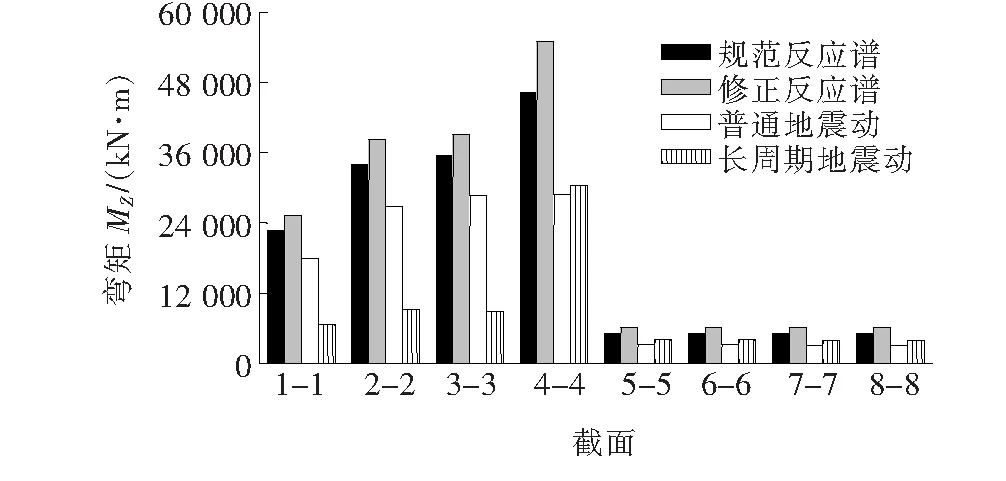
(d) 弯矩MZ

(e) 弯矩MY图10 E2地震作用下结构内力响应

由图7可知：① 在E2地震作用下，桥梁在修正反应谱分析的位移响应和规范反应谱相比，X、Y、Z方向的平均位移分别增加了17.43%、20.91%、12.96%；② 长周期地震动的时程计算结果和普通地震动相比，X、Y、Z方向的平均位移分别增加了19.72%、39.06%、2.1%。该桥的长周期特性明显，考虑长周期地震动因素的修正反应谱计算结果比规范反应谱的大，且长周期地震动的位移响应比普通地震动的大；

③ 在长周期地震动作用下，X方向的平均位移比规范反应谱作用下的平均位移大12.77%，却比修正反应谱的平均位移小3.98%。说明桥梁低阶模态的位移响应对结构的最终响应影响较大，且该桥受长周期地震动的影响较大，规范反应谱的计算结果不能直接作为抗震设计的结果，对结构安全不利；④ 修正反应谱考虑了长周期地震动的作用因素，计算结果较为保守，对结构的抗震设计较为安全。

由图8可知：① 在E2地震作用下，桥梁在修正反应谱分析的内力响应均大于规范反应谱，说明该桥受长周期地震动的影响较大；② 反应谱计算的内力响应整体均大于时程计算的内力响应，但对于桥梁的侧向弯矩Mz而言，反应谱作用下的主梁侧向弯矩整体均大于时程的计算结果，但在长周期地震动作用下，桥墩的侧向弯矩比规范反应谱的计算结果大8.32%，比修正反应谱的计算结果小6.89%；③ 结果说明规范反应谱未考虑长周期地震动因素，在桥墩的内力响应计算偏低，对结构抗震设计安全不利，而修正反应谱计算结果较为安全可靠。

4 结论

(1) 通过比较普通地震动反应谱、长周期地震动反应谱和规范反应谱的变化趋势，得出规范位移反应谱在长周期段随周期线性递增，与实际地震动位移反应谱的变化趋势差异显著，统计特征明显不符，说明规范位移反应谱出现严重失真，需对规范反应谱修正。

(2) 针对规范反应谱的缺陷，选取了考虑长周期地震动的各类场地612条地震记录进行统计分析，提出衰减指数线性变化的修正方法，对规范反应谱长周期段进行合理修正，并确定了修正加速度反应谱的相关参数，为实际工程的抗震设计和计算提供可靠依据。

(3) 通过某一长周期特性明显的高墩连续刚构桥进行有限元验证，在长周期地震动作用下，结构在X方向的平均位移响应比规范反应谱的大12.77%，比修正反应谱的小3.98%；桥墩的侧向弯矩Mz比规范反应谱的大8.32%，比修正反应谱的小6.89%。说明长周期桥梁结构受长周期地震动的影响显著，规范反应谱在X方向的位移响应和侧向弯矩响应和长周期地震动的响应结果相比偏低，对结构抗震设计不安全；修正反应谱的位移和内力响应结果偏大，较为保守可靠，对结构的抗震设计更为安全合理。