基于灰色理论的船舶应急物流优化模型仿真

孙宇博，胡 晶，刘 鑫

(1. 徐州工程学院管理工程学院，江苏 徐州 221008；2. 中南大学计算机学院，湖南 长沙 410083)

1 引言

自进入21世纪以来，地震等突发性灾害以及各类重大事故频发，海上突发重大事故更是频频发生[1]。我国的领海面积巨大，海岸线绵长，靠海谋生的渔民不计其数，如何为海上应急物流选取一条最佳的路径通道，成为物流领域亟待解决的难题之一[2]。

汪贵庆[3]等人提出基于精英蚁群算法的交通最优路径研究。该方法首先基于Petri网络，构建精确的多因素交通路网模型；再利用精英蚁群算法对信息浓度进行初始化引导，并采用相互约束的方式寻找两条以上的路径；最后通过对路径信息素浓度的计算，寻找出最佳的路径。该方法由于未能考虑物流配送过程中的约束条件，所以该方法选取的配送路径配送时间较长。樊相宇等人[4]提出基于道路堵塞及顾客时间要求的快件配送最优路径选择。该设计方法首先对交通网络的关键边以及配送的网络特征进行计算；再根据时间要求，对不同的路径进行分析；并依据最短路径上的各边特点，对各边对应的路径进行计算，选取一组备用路径；最后将符合时间要求的路径作为运输的最佳路径，完成路径的选择。该方法选取路径的运输安全性能较低，且船舰疏散性能较差。除此之外，常用的路径优化方法还有基于有向图规划的船舶物流运输最优路径选取算法。依据有向规划方法对物流运输时的路径冲突分流点进行确定；再依据深度优先遍历算法对分流点进行计算，并逆序打印每一条路径的计算结果，从中选取一条最优路径，以此完成物流的最佳路径选取，该方法选取路径的配送距离长。

为解决上述路径选取时存在的问题，提出基于栅格GIS的海上应急物流最优路径选取方法。

2 路径优化

首先基于栅格GIS技术对海上应急物流在配送时存在的影响因素进行分析。再利用智能优化算法优化配送路径[5]。由于海上物流配送路径错综复杂，在运输中会产生大量的数据，对这些数据的处理效果会对物流运输路径优化效果产生影响[6]。然而现有方法不能对数据进行有效处理，因此，本文采用栅格GIS技术对单格栅格数据与多格栅格数据同时进行矢量化处理，根据数据处理结果再对海上应急物流在配送时存在的影响因素进行分析，可以提升路径优化效果。

2.1 挖掘约束条件

海上应急物流在进行配送时，船舰会将各个港口作为节点，执行物流的配送任务。而在应急物流的配送过程中，会受到各类约束条件的影响，所以采用栅格GIS技术对应急物流配送期间可能存在的约束条件进行必要的特征点挖掘，成为配送的关键[7]。

在选取应急物流配送路径时，需要考虑时间约束问题，过程如下所示

∀d∈Dab，[T1+T2]≤Tab

(1)

式中，该次配送的局部最优路径为d，物流配送的出发点和终点分别为a和b，出发点与终点之间存在的全部路径用Dab表示，物流规定的配送时间上限为Tab，而船舰在物流配送过程中的配送时间为T1，到达时间为T2。

其次，应急物流在配送过程中要考虑中转次数所带来的影响，中转次数约束条件如下式所示

(2)

由于船舰所航行的每一条航线都有船舰运力，船舰在配送时不可超过极限运力，因此，物流配送会受到航线运力的约束，将此约束条件表示为

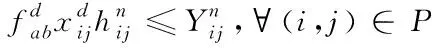
(3)

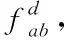
2.2 构建路径优化模型

整合应急物流在配送时产生的相关数据，如船舰装载量、航线运力等，将整合后的数据归一到一个数据集中。设定数据集内的数据量为N，数据集中每个数据个体的体积为UV。依据随机生成理论生成物流配送航线；在此基础上，继续生成第二组路径组合及航线，直至完成配送。匹配过程中，若无中转港口，则将本次配送看作直达配送，以此构建有m个解的路径优化模型[8]。

基于模型的特点以及获取的约束条件，与目标函数进行结合，搭建配送的适应度函数，过程如下式所示

(4)

式中，搭建的适应度函数为S，模型中的目标函数为M，函数中的惩罚系数为λ，且λ为无限大。

若构建的函数不能满足全部的约束条件，则获取的配送路径就为局部最优而不是全局最优，为了获取全局最优解，采用群智能优化算法搜索局部混沌区域。

2.3 搜索局部混沌区域

路径优化后只能获取路径的局部最优，而不是全局最优。因此，基于改进的群智能优化算法，对备选的配送路径进行优化处理。设置映射混沌序列为

φi+1=kφi·(1-φi)，i=1，2，…，q-1

(5)

式中，搜索的随机参数为φi，搜索数量为q。

在更新完成整个群体的数据后，利用搜索策略对海上应急物流配送路径的局部混沌区域进行搜索，过程如下式所示

Xm=(1-σ)X0+σ[r2+φm(r1-r2)]

(6)

式中，获取的路径搜索候选解为Xm，经过高斯变异策略获取的最优解为X0，混沌序列中的元素表示为φm，最优解空间中的上限与下限分别为r1和r2，搜索过程中控制收缩程度的参数为σ。

依据上述计算过程，对海上应急物流的全局域混沌局部搜索，实现海上应急物流的备选配送路径优化。

3 最优路径选取

利用灰色关联系数对上述优化的路径进行计算，从而实现海上应急物流的最优路径选取[9]。

3.1 路径评价指标

首先，设定备选路径有z个，评价指标有o个，基于灰色理论构建一个数学模型，过程如下式所示

R=W×η

(7)

式中，海上应急物流的备选路径综合评价矩阵为R，且R={rz，z=1，2，…，n}，权重分配矩阵为W，且W={wo，o=1，2，…，m}，基于熵值法确定决策指标权重为wo，η为关联系数矩阵。

3.2 构建评价指标集

基于获取的路径评价指标，对备选路径进行量化处理。经过量化后，评价指标会具备一致性特征，以此可对其进行关联系数的计算。将指标分为“小且优指标”和“大且优指标”，并借助下式进行求解

(8)

式中，备选路径z的第o个指标初始值为x′zo，而xzo为归一化后的第z个路径上的第o个指标。最后基于上述处理过程，构建规范的评价指标集X={xzo}(n×m)。

3.3 最优指标集

整合备选路径中不同指标的最优值，形成一个最优指标集，过程如下式所示

X0=(xo，o=1，2，…，m)

(9)

式中，获取的最优指标集为X0。

3.4 计算指标权重

通常情况下会根据层次分析法对指标权重因子进行确定，但是受主观因素影响，评价结果不客观，所以要利用客观赋权法来计算评价指标的权重。各个评价指标的决策信息可用eo表示，表达过程如下所示

(10)

式中，eo为指标决策信息，lnxzo为第z个备选路径上第o个指标的不确定值。而第o个指标的评价数据的离散程度如下式所示

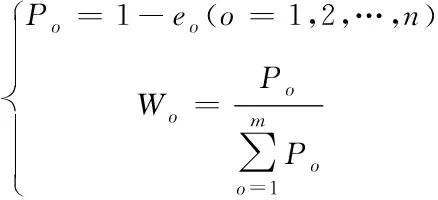
(11)

式中，获取的指标离散程度为Po，指标的权重因子为Wo。

3.5 计算关联度

基于上述计算结果，利用灰色系统理论中的灰色关联分析法对海上应急物流备选路径的关联程度进行计算[10]。首先将获取的最优指标集{x0(k)}={x0(1)，x02，…，x0(k)}作为参考数据列，并将各个指标集{xo(k)}={xo(1)，xo(2)，…xo(k)}作为被比较数列，且(o=1，2，…，n)(k=1，2，…，m)。依据下式计算备选路径中第z个路径上第o个评价指标的关联系数δz(o)，过程如下式所示：

δz(o)=

(12)

3.6 综合评价

最后对备选路径的优劣进行排序，从而选择出海上应急物流的最优路径。选择流程如图1所示。

图1 海上应急物流的最优路径选择流程

4 实验

为了验证所设计最优路径选择方法的整体有效性，需要对此方法进行测试。

4.1 实验结果及分析

分别采用基于栅格GIS的海上应急物流最优路径选取方法(方法1)、基于精英蚁群算法的交通最优路径研究(方法2)、基于有向图规划的船舶物流运输最优路径选取算法(方法3)进行测试；

1)随机选定一块海域，对方法1、方法2以及方法3的海上应急物流配送时间进行测试，测试结果如图2所示。

图2 三种方法的物流配送时间测试结果

依据图2可知，方法1测试的海上应急物流配送时间均在55小时至56小时之间。方法2经过多次实验可知，海上应急物流的配送时间在58小时至60小时之间。而方法3经过多次测试后可知，海上应急物流的配送时间在61小时至64小时之间。综上所述，方法1所选取的最优路径在物流配送时的配送时间短。

2)对方法1、方法2以及方法3所选取的最优路径的运输距离进行测试，测试结果如图3所示。

图3 三种方法所选路径的运输距离测试结果

依据图3可知，方法1所选路径的海上应急物流运输距离要低于方法2以及方法3。方法3在测试初期所选路径的运输距离几乎与方法1持平，但随着实验次数的增多，方法3所检测出的路径运输距离均为三种方法中最长的。这主要是因为方法1在物流配送前考虑了配送过程中可能出现的约束条件，所以方法1选取路径的运输距离短。

3)对方法1、方法2以及方法3的船舰疏散性能进行测试，测试结果如图4所示。

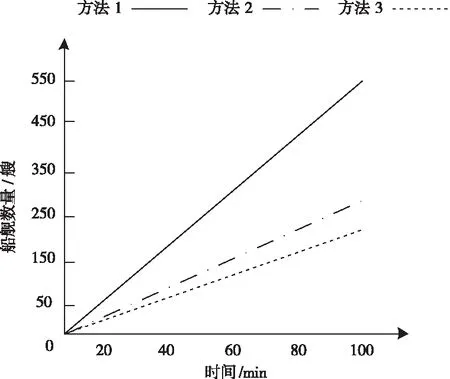
图4 三种方法的船舰疏散性能测试结果

依据图4可知，方法1在100分钟内可以有效地对该路径上的550艘船舰进行疏散，而方法2只能疏散不超出350艘的船舰，方法3是三种方法中性能最差的，只能在100分钟内疏散不超过250艘船舰。综上所述，方法1所选路径的船舰疏散性能高。

4)对方法1备选路径优化前后的路径运输安全性进行测试，测试结果如表1所示。

表1 方法1路径优化前后运输安全性测试结果

依据表1可知，基于栅格GIS的海上应急物流最优路径选取方法备选路径在优化前的运输安全性最高可达94.1%，而考虑约束条件的备选路径运输安全性最高可达97.2%。综上所述，经过优化后的备选路径运输安全性能更好。

5 结束语

随着近几年我国发生的严重突发事件增多，对于海上应急物流的选取变得更加严苛。针对应急物流配送过程中路径选择方法中存在的问题，提出基于栅格GIS的海上应急物流最优路径选取方法。该方法首先利用栅格GIS技术与群智能优化算法对备选路径进行优化；再基于灰色关联理论对备选路径的灰色关联度进行计算，并依据计算结果选取最优的路径进行配送。实验结果表明，该方法的最优路径配送时间、配送距离、船舰疏散性能以及输送安全性均优于传统方法。