基于小世界复杂网络的水文诊断模型仿真

裴源博，赵雪花

(太原理工大学水利科学与工程学院，山西 太原 030024)

1 引言

自然环境在气候与人类各种行为活动的影响下，始终处于不断变化的状态，其中水文系统也会出现明显改变。现阶段，水资源短缺、承载能力下降已经严重威胁社会可持续发展。由于水文系统的平衡关系被破坏，水文序列表现出的一致性特征也逐渐消失，统计规律将无法用于对未来情况的预测。非一致性、变异性已经成为水文序列的新特征。当水文系统出现异常时，也代表着水循环过程遭到破坏，这会导致较多的工程和科学问题。例如，因水文系统出现变异，致使已有关于水文分析的成果遭到质疑；增加水文序列演变的复杂性，进而造成水资源管理的不可控性。这些改变对传统的水文预测工作敲响警钟，一些科研人员已经将如何准确诊断水文序列的变异情况提上研究日程。

文献[1]提出基于滑动偏相关算法的水文序列变异诊断方法。选取塔里木河流域的某时间段径流资料，利用Pearson相关系数分析径流和天气状况之间的相关性；引入滑动窗口技术完成水文气象要素的联合序列异常诊断，并通过双累积曲线方式完成验证。文献[2]提出基于自回归模型的水文序列异常识别算法。将初始序列及其相依成分的相关系数当作拟合指标，利用信息熵函数形式作为自回归模型准则，构建诊断模型。除上述方法外，还有学者利用Mann-Kendall秩次检验法对水文序列的突变性与非一致性进行诊断。通过该方法识别突变点，同时采用Morlet小波分析序列周期特征，结合突变点诊断、周期分析与驱动机制三个方面分析序列的非一致性变化特点。

水文序列作为观测样本，在气候与人文因素影响下会出现突变现象，通常情况下，突变具有多尺度特征，不同原因会导致不同时间与不同等级的突变。而上述方法并没有结合水文序列的非线性特征，虽然能够诊断出突变情况，但是诊断结果并不全面。复杂性正是当前水文研究的主要特征，为此，本文利用复杂性理论实现非一致性水文序列突变诊断。水文系统的复杂性主要表现在它是由天文、大气、生物与人类共同作用与交叉的结果，应结合多方面进行考量。分析在不断变化的环境中，水文序列表现出的非一致性现象，为突变诊断提供更加可靠的方法。

2 水文序列突变的驱动因子与统计特征分析

2.1 突变驱动因素分析

在不断变化的自然界中，水文变化一般由多种因素相互作用形成。这些因素之间的作用关系如图1所示。

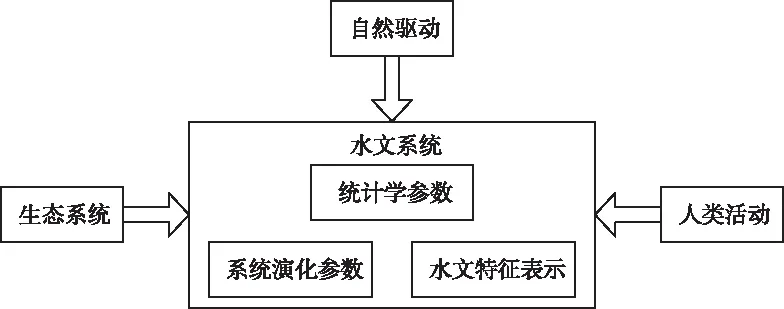
图1 驱动因素关系图

1)自然变化

在人类干扰程度较小的情况下，水文变化一般受到自然因素的驱动，呈现出较为平稳的波动趋势，且不断循环。其时间序列便于预测与管理，不会出现较大幅度改变。

2)气候变化

近年来全球变暖已经引起全世界的关注，相关研究显示，暴雨、干旱等极端天气发生频率正逐年提高。而气候变化大多与人类活动相关，可利用区域水循环来改变水文系统。如果不考虑人类活动对其产生的影响，气候驱动因素对水文系统的影响微乎其微。

3)人类活动

自首座水坝建成以来，水文就与人类活动有着密不可分的联系。现阶段，人类活动对世界上82%以上的水资源均存在直接影响。此外，大多数人口都面临非常严重的水资源威胁，同时也影响着生物的多样性。由于人口迅猛增长，人们对水资源的依赖更加强烈。工业与经济发展也对水资源的需求量进一步增大，供需矛盾愈演愈烈。

社会行为的特征与差异性，使人们在面对水文问题的观点与做法上形成区别。所以，必须从根本上分析人类活动的影响，构建行为和用水规律之间的关系。针对当前情况，人类行为对水文产生的影响分为直接与间接两种。其中，前者代表从河流取水，用于生活、灌溉与工业等方面，主要目的是提高生活水平；后者则是通过人类一系列活动导致水环境产生改变，例如林地与土地建设等均会造成产汇流变化[3，4]。

综上所述，水文变异并非受到单个因子驱动，而是在自然与社会共同作用下产生的，且二者相互影响形成一个复杂反馈过程。

2.2 水文突变统计特征表现

现有水文设计多数基于一致性假设，但是受到各类因素影响，一些地区表现出的水文一致性被破坏，这对水文设计产生严重影响。因此，变异诊断已经成为水文设计的基础，诊断结果的准确性关乎水利工程建设方案是否可行。如果方案出现问题，会有严重事故发生，对人们生命与财产安全带来威胁。为准确判断出水文序列是否出现变异现象，必须对水文系统的特征有一定了解。

将水文序列描述为x1，x2，…，xt，通常记为{X(t)}。其中，x1，x2，…，xt代表序列的t个实际值。结合时间序列相关理论，可利用下述统计特征对水文序列进行描述。

1)概率分布

通过分布函数[5]表示某水文过程的所有统计特征。若水文序列为任意变量，则一维分布函数表示为

F(x，t)=P[X(t)≤x]

(1)

与其对应的一维密度函数为

f(x，t)=∂F(x，t)/∂x

(2)

同理，X(t)的n维分布函数公式如下

F(x1，…，xn，t1，…，tn)=P[X(t1)≤x1，…，X(tn)≤xn]

(3)

2)均值

均值能够体现序列平均水平，属于水文序列的主要位置特征，其表达式如下

(4)

3)方差与变异系数

方差与变异系数分别表示水文序列的绝对、相对离散情况，计算公式如下

σ(t)2=E[X(t)-μ(t)]2

(5)

Cv=σ/E(X)

(6)

3 基于复杂性理论的水文序列突变诊断

3.1 复杂网络模型构建

由于水文系统受到较多复杂因素影响，本文结合复杂性理论，建立复杂网络。该网络的拓扑无需考虑节点位置与边的形状。

将网络抽象为网络模型图G(V，E)，其中，V代表节点集合，网络中节点数量为|V|；E(1e，2e，…，me)表示边集合，记为|E|，节点集合中的点与边互相对应。

假设该网络中共存在8个节点与9条边，则从下述几个维度对该网络进行分析。

1)最短路径

节点i与j的最短路径为dij，描述由i到j的全部路径中包含边数最少的路径，计算公式如下

(7)

式中，N为节点总数量。

2)度及度分布

节点的度ki就是与节点i相连的全部邻居数量，表达式为

(8)

3)集聚系数

在该网络中，任何节点之间的连线都具有随机性[6]，其集聚系数表示为C=p，其中，p代表两点相连的概率。对于该系数的分析可以得出网络复杂程度等有用信息。集聚属于网络基本特征属性，Ci即为网络中各点集聚系数C的平均值

(9)

式中，ki代表节点i的邻居数量，Ei代表ki个点具有的真实边数。

4)节点介数

在复杂网络模型中节点介数是体现该节点重要性的指标，计算公式如下

(10)

式中，njk表示节点j和k的最短路径总数。

综合上述维度可知，复杂网络模型并非完全规则或完全随机。因此，本文建立一个介于规则与随机之间的小世界复杂网络模型，建模过程为：

1)建立包含N个节点的最近邻耦合模型，确保节点和其K/2个邻居节点相连。

2)做随机重连，在保证一个节点不变的情况下，根据概率p实现边的重新连接。将规则的模型转换成小世界网络模型，并通过p来调节大小。当p=0时，属于规则模型，当0

(11)

3.2 变异诊断

利用上述构建的复杂网络模型，通过最小二乘算法确定模型目标函数[7]，获取全局最优解，即为变异点位置。该方法最大优势是决策者能够设计不同变异点间存在的最小距离，完成准确诊断。诊断过程如下：

1)假设水文时间序列表示为{y(ti)}i=1，…，n。

2)当使用最小二乘算法完成未知变异点时间序列拟合时，如果要使残差平方和为零，则最优拟合策略为将序列中全部点进行连接。所以，必须设置约束条件，控制分段拟合数量与步长。假设序列{y(ti)}分为m′+1段，m′为变异点数量，最优分段线性方程表示为

(m′=0，…，m；Tm′≤ti≤Tm′+l)

(12)

式中，Tm′代表变异点位置，设置T0=0，Tm′=tn，b表示回归系数矢量。

假设水文序列中出现3个变异点

y(ti)={y(t1)，y(tbp(2))，y(tbp(3))，…，y(tbp(m′))}

(13)

式中，tbp(2)、tbp(3)与tbp(4)描述变异点出现的位置，分别构建如下回归方程

y(ti)=a1ti+c1，i=1，…，bp

(14)

y(ti)=a2ti+c2，i=bp(2)+1，…，bp(3)

(15)

y(ti)=a3ti+c3，i=bp(3)+1，…，bp(4)

(16)

y(ti)=a4ti+c4，i=bp(4)+1，…，m

(17)

根据变异点具有的连续性特征，获得下述联立方程

c2=c1+(a1-a2)tbp(2)

(18)

c3=c1+(a1-a2)tbp(2)+(a2-a3)tbp(3)

(19)

c4=c1+(a1-a2)tbp(2)+(a2-a3)tbp(3)+(a3-a4)tbp(4)

(20)

4)为避免变异点区间设置存在主观性，利用构建的复杂网络模型分别获取变异点的置信区间[8]与变异点前后时间序列的显著性。

假设变异点两侧的回归方程表示为：

RLa=Aa(X-AvXa)+AvYa

(21)

RLb=Ab(X-AvXb)+AvYb

(22)

式中，Aa与Ab分别代表变异点前、后回归系数，AvXa和AvXb分别描述变异点前、后全部数据的横坐标均值。

由于

(23)

因此，变异点左右两侧置信的上、下限分别表示为

L上=(X，Yla+ts.StDevYc)

(24)

L下=(X，Yla-ts.StDevYc)

(25)

R上=(X，Ylb+ts.StDevYc)

(26)

R下=(X，Ylb-ts.StDevYc)

(27)

根据变异点的置信区间，准确确定序列变异点位置，完成序列突变诊断。

4 实验数据分析与研究

为证明所提方法对于水文序列突变诊断的可行性，进行仿真。将渭河流域当作诊断目标，该段流域长度是734km，面积为13.11万km2。此地地形差异较大，呈现出东低西高趋势，最大高程差为2500m之上，流势变化缓慢，河道淤泥较多。此外，水系发达，支流众多，但近年来的径流量出现整体下降趋势。具体情况如表1所示，水文循环示意图见图2。

表1 渭河流域多尺度特征表

图2 渭河流域水文循环特征示意图

由于本文方法是基于复杂性理论的分析，因此结合该地区实际情况，选择诊断指标，将该指标引入到复杂网络模型中，再通过回归变异诊断，输出最终诊断结果。本文选择的指标如表2所示。这些指标不但要体现流域特征，还要保证指标之间存在一定影响与制约。

表2 该地诊断指标表

结合上述诊断指标，利用文献[1]、文献[2]、文献[3]方法与本文方法对淮河流域2011年-2019年的水文序列突变情况进行诊断，诊断结果如图3-6所示。

图3 文献[1]方法诊断结果

图4 文献[2]方法诊断结果

图5 文献[3]方法诊断结果

图6 本文方法诊断结果

相关水文资料表明，渭河流域在2011-2019年期间，共出现三次水文序列突变状况，时间点分别是2014年、2016年与2017年。由图6可知，本文方法在这三个时间点上的变异系数尤为突出，而文献[1]和文献[3]的方法都少诊断了一个变异点，文献[2]方法的变异曲线始终较为平稳，虽然变异系数有所改变，但趋势较弱，并不明显。资料显示，在2014年，该流域煤炭开采大幅增加，而在2016与2017年均修建了多个水库，洪峰减少。因此，本文诊断结果与历史资料相符，表明该方法诊断结果更加可靠。

5 结论

为准确诊断出水文序列的变异情况，本文构建了复杂网络模型，再结合回归变异算法完成序列变异诊断。在实验过程中，综合当地水文特征，设置多个诊断指标，给出可靠的诊断结果。现阶段，基于复杂性理论的水文序列突变诊断还处于起步阶段，尚未形成全面的诊断体系。在今后研究中，需引入混沌分析等方法，提高诊断速度，将多诊断方法相结合，全面体现序列的变异特征，避免单一方法得出的结果不够科学合理。