通讯网络密文信息篡改快速恢复数学建模

刘淑芬，钟晓林，贺 煦，刘咏梅

(1. 南昌交通学院，江西 南昌 330100；2. 江西师范大学，江西 南昌 330022)

1 引言

网络为信息传输带来极大便利，其中图像作为一种包含文字、图形等多种信息的传输方式，保证其数据安全十分重要。不然则可能会导致个人信息泄露、隐私曝光[1]。针对上述信息安全问题，急需一种通讯加密技术，加强网络信息的安全性。密文加密技术是一种比较常见的方法，一般与防火墙技术搭配使用，不但可以改善信息系统的安全性，还可以提高保密效果[2]。由于信息技术的迅猛发展，人们对网络数据保密工作极其重视。

目前，常用的信息篡改恢复方法主要有基于纠错编码的图像篡改恢复方法和面向图像篡改可恢复的认证水印方法，前者对图像原始特征进行采集，将采集结果生成为校验码，在对校验码进行Arnold置乱后，嵌入至原始图像中，并采用校验码对经过篡改的图像进行恢复。结果表明，该方法能够准确检测篡改位置，并对其进行定位。后者首先获取图像的灰度均值，然后对图像进行混沌映射加密，并将水印信息嵌入至图像中，以此实现细小篡改信息的检测。结果表明，该方法能够提升对篡改信息的敏感性，且安全系数较高。上述两种方法均能够提高图像质量，展示出较强的恢复效果。但是忽略了图像的模糊性，例如在图像恢复过程中，某像素点到底是不是此图像中的边缘点，这属于带有模糊性的问题。

针对图像固有的模糊性，随着模糊理论的不断完善，本文利用模糊数学理论构建通讯网络密文信息篡改快速恢复数学模型。通过模糊数学理论对传输信道作出综合评价，根据信道重要等级，区分边缘块[3]与平滑块[4]，完成密文信息篡改快速恢复。

2 基于模糊数学理论的信道等级评价

模糊评价方法实质上是一种模糊运算法则，经常出现在模糊数学中，需利用非线性方程对论域进行评价，达到综合量化目的，以此获得能够比较的量化评价结果。在通讯网络系统中模糊综合评价算法的步骤如下：

1)确定因素集合

待评价的全部因素集合被称为因素集，在通讯信息系统中能够产生影响的因素非常多。就篡改恢复而言，对通讯质量产生最大影响的信息差错是最迫切需要得到恢复的[5]。篡改恢复算法中根据网络恢复的优先级，将评价因素集合大致分成下述两级：

一级因素

U=U1·U2·U3

(1)

二级因素：

U1=U11·U12·U13

(2)

U2=U21·U22·U23·U24·U25·U26

(3)

U3=U31·U32·U33

(4)

2)建立评语集

评语集合即为针对评价目标，评价者对其作出全部评价结果的集合。若存在m个评价结果，则评语集合能够记作

V=V1，V2，V3，…，Vm

(5)

式中，Vm表示最后一个评价结果，该方案中涉及的信息系统评价集合为

V=V1，V2，V3，V4，V5

(6)

3)确立指标权重集合

任意一个评级因素对评价目标均存在不同程度的影响，所以在评价过程中需对不同因素所占权重的差异性进行分析，经过专家评分获得这些因素的权重值。

与因素集合为U相对的权重集合为A，则一级权重集合表示为

A=A1，A2，A3Ai≥0

(7)

且满足如下条件

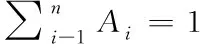
(8)

式中，Ai代表第i个一级权重集合中的因素权重。二级权重集合为

A1=A11，A12，A13，A14

(9)

A2=A21，A22，A23，A24，A25，A26

(10)

A3=A31，A32，A33Aij≥0

(11)

式中，Aij代表第i个二级权重集合中第j个元素。

4)构建隶属度矩阵

专家能够对全部评价因素的隶属度[6]进行判定，利用Rij表示隶属度，其代表的是评价主体对任意一个评价因素在Ui角度出现的Vj评价的可能性大小，同时也表达了第i个因素评价下第j个等级的隶属度，则第i个因素的隶属度矢量为

Ri=Ri1，Ri2，…，Rim

(12)

且符合下述要求

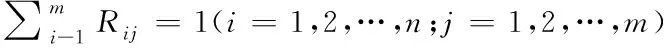
(13)

n个因素具有的隶属度矩阵记为

R=R1，R2，R3，…，Rn

(14)

5)模糊评价模型

为全面体现出评价因素对评价对象的影响，且能够获取和实际情况相符的评价结果，在已知权重集合A和隶属度矩阵R的条件下建立的模糊评价模型如下

Bi=A°iRi(i=1，2，3)

(15)

式中，(∘)选取的是(+，×)算子，则有

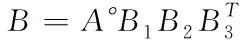
(16)

综合得分利用加权思想[7]进行计算，假设网络通讯信道评价等级是(5，4，3，2，1)，则综合得分为B°54321T。

将上述构建的综合评价模型应用到密文信息篡改恢复中，利用非线性方程评价论域，实现综合量化，确定传输信道的优先级，以提升恢复方案效率。

3 网络密文篡改检测与快速恢复数学建模

3.1 差错检测

为实现篡改恢复，必须对篡改现象进行检测，也就是对差错的精准定位。当检测到有篡改现象出现时，构建再同步避免差错扩散到正常块中。本文通过编码器[8]生成的指示信息来实现差错检测。

对于图像帧内编码差错检测，需要获取块差值指示数据、宏块再同步的置信度数据以及过恢复检测数据。

1)块插值指示数据

2)宏块再同步的置信度检测数据

3)过恢复检测数据

如果接收的块中只存在轻微影响视觉效果的较小误码，说明这种篡改现象没有被基线解码器检测到。这时如果放弃全部能够利用的信息来激活篡改机制恢复块，则获得的视觉质量通常更差，此种状况为“过恢复”。要想避免此现象，检测到差错后，在恢复之前需对篡改程度进行评估。

当接收的块在视觉上存在明显被篡改痕迹时，其DCT系数中的最高位会出现变化，因此可根据DCT系数来估计视觉破坏程度。为提高检测效率，在编码时只需要对块的DCT系数最高两位构成2bit的检测数据，通过解码器检测块的破坏程度，评估是否存在“过恢复”现象。

针对频率资源较为有限的图像通讯，减少信息传输量具有重要意义。如何将指示数据嵌入到待传输的网络密文中，且不增加编码开销是需要解决的重点问题。本文利用DCT系数强制性修改方式嵌入指示数据。

如果被嵌入的信息比特为b，则根据以下原则修改选取的块非零DCT系数

(17)

式中，Ci，j表示DCT矩阵系数，Ki，j代表量化矩阵系数。

解码过程中，根据下述原则从当前块的非零DCT系数中获取指示信息

b=Cmod 2

(18)

3.2 篡改快速恢复数学建模

3.2.1 基于模糊理论的空间域图像恢复

在模糊理论中，模糊熵是图像处理的重要概念，密文信息图像的模糊熵需将变量从一维空间扩展到二维空间中。如果大小是M×N且灰度级为L的密文图像通过X=[x(i′，j′)]MN描述，在此图像内选取大小是n×n的某邻域Wn(i′，j′)

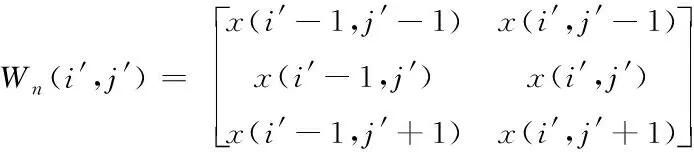
(19)

式中，(i′，j′)代表中心点坐标，将此邻域[9]中的灰度值作为论域，再构建模糊集合A′，则式(19)中的邻域元素对集合A′的隶属度函数表示为

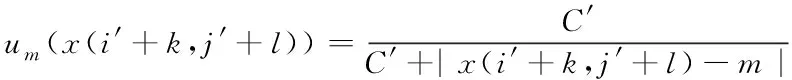
(20)

式中，m表示集合A′的特征值，C′属于常数，其作用是确保0.5≤um(i′，j′)≤1。则将图像模糊熵表示为

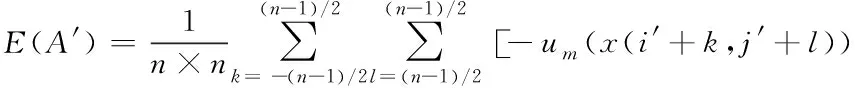
(21)

当n=N或n=M时，上述公式表示图像整体模糊熵。此外，当特征值m=x(i′，j′)时，模糊熵大小即为像素的灰度值与附近灰度值差异的大小[10]。

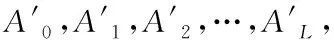
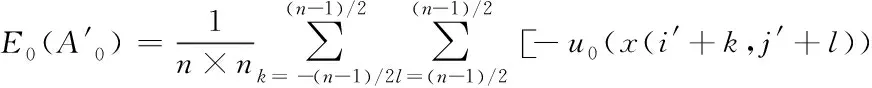
(22)

利用式(22)可以获取L个模糊熵测度，从中选取最小测度，再将与此测度相对的灰度值赋予选定邻域的中心像素。以此类推，遍历整个图像后，即可获得空间域恢复后的图像。

3.2.2 基于模糊理论的变换域图像恢复

(1)模糊增强算子

针对灰度级为L，大小是M×N的密文图像X，其算子通过下述隶属度函数描述

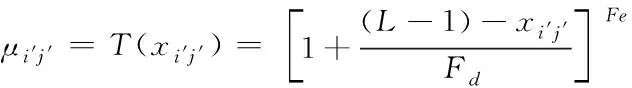
(23)

将该图像从空间域变换到模糊域中，Fe与Fd分别表示隶属度函数中模糊参数与倒数模糊参数。经过上述隶属度处理后，获得如式(24)所示的模糊域图像

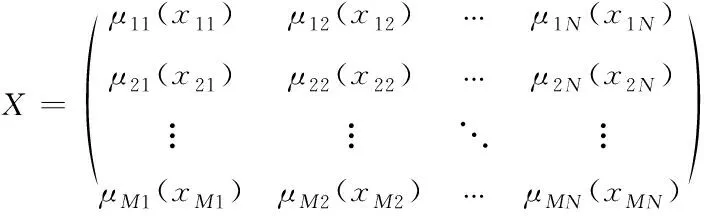
(24)

此时将xc当作渡越点，μc表示阈值，所以能够计算出模糊增强算子大小

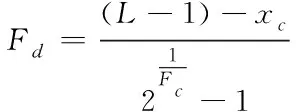
(25)

利用上述变换方法获得模糊域图像后，通过以下隶属度变换函数对模糊域图像做进一步处理

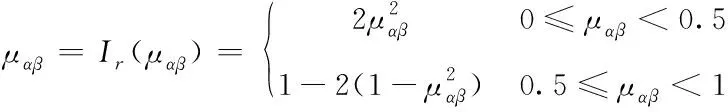
(26)

式中，I为迭代运算，r属于正整数，代表迭代次数，可结合不同需求选取迭代次数。

在确定模糊增强算子后，需对阈值进行选取，假设各像素值的概率表示为

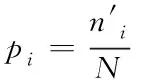
(27)

将图像中的像素灰度级被整数g划分为两类，分别表示为C1={0，1，…，g}与C2={g+1，g+2，…，L-1}。假设C1类中像素数量占该图像总像素数量的比率与平均灰度值分别为w1(t)与u1(t)，则有

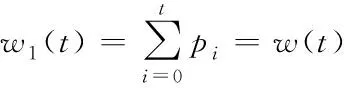
(28)

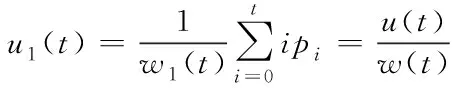
(29)

第二类像素数量占图像总像素数量的比率与平均值分别记作w2(t)和u2(t)，则阈值T*可通过下述公式确定

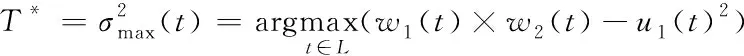
(30)

此种阈值确定方式，避免了人工介入进行多次尝试的弊端，可以结合图像灰度信息选取最优阈值。

确定模糊增强算子与阈值后，利用下述逆变换函数将图像变换至空间域中，达到篡改图像恢复的目的

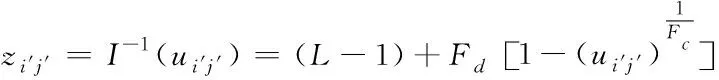
(31)

上述即为利用模糊数学理论进行网络密文信息篡改快速恢复建模的全过程。

4 仿真数据分析与研究

为测试模型性能，将256×256×8的灰度密文信息图像作为仿真目标。对该图像进行剪切、替换等篡改。在仿真中对于不同误码率，使用二进制对称噪声信道模型模拟通讯信道。将篡改检测概率与图像峰值信噪比作为评价指标，计算公式分别如下

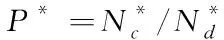
(32)

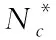
针对大小为MN的密文图像f*(x′，y′)，信噪比高表明恢复性能较好，其信噪比计算公式如下

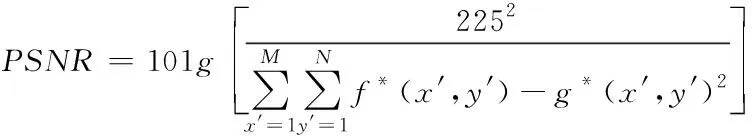
(33)

式中，g*(x′，y′)代表去噪后的图像。

将基于纠错编码的图像篡改恢复方法(方法1)和面向图像篡改可恢复的认证水印方法(方法2)与本文方法对上述两个指标进行对比，结果如下：

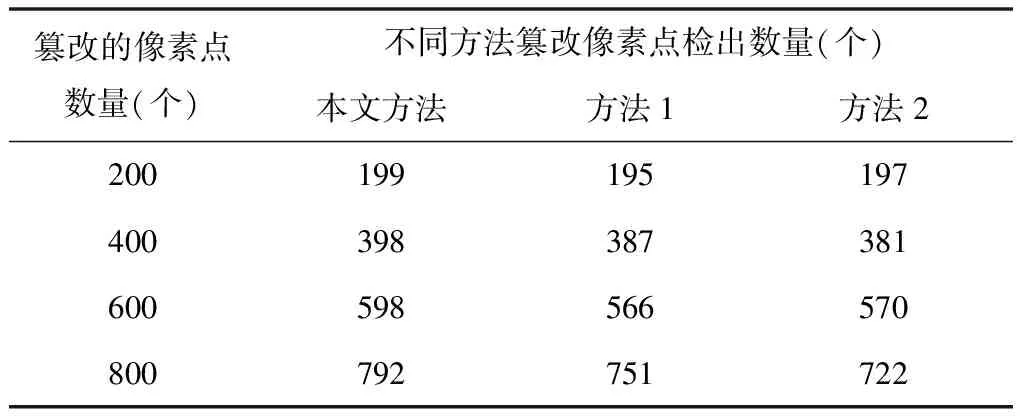
表1 不同算法篡改检出率对比结果

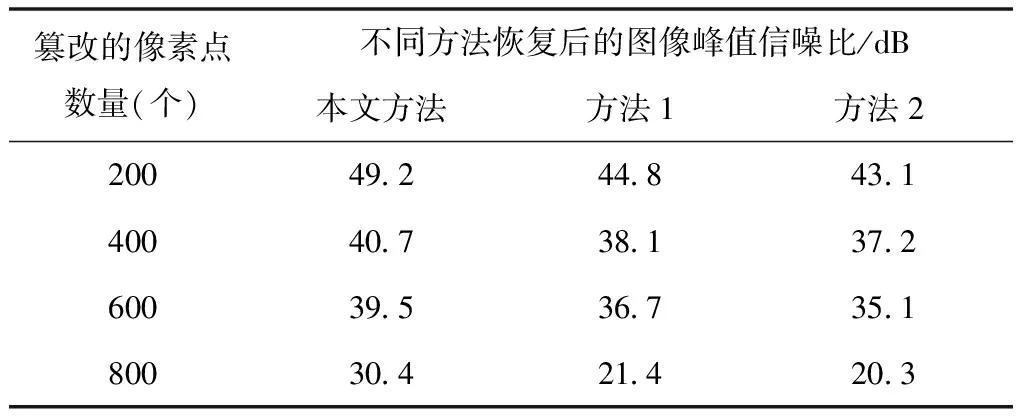
表2 不同方法恢复效果对比

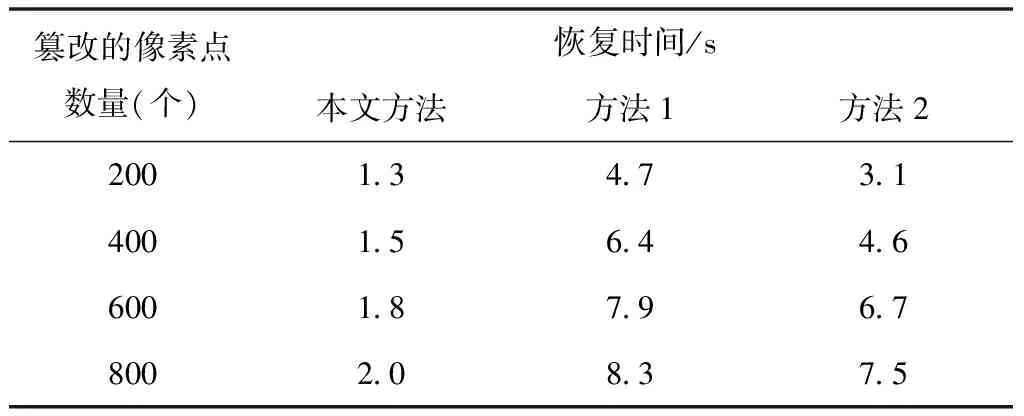
表3 不同方法恢复时间对比

由表1、表2和表3可以得出，所提方法可以更加全面、快速地检测出被篡改的像素点，且恢复后的图像信噪比更高。这是因为本文方法能够全面检测出篡改像素点，有助于提高恢复后的图像信噪比。

图1为不同方法下的图像信息篡改恢复效果对比结果。

图1 不同方法恢复效果图

根据图1可知，本文方法能够有效恢复篡改信息，恢复效果较好。这是因为本文方法利用模糊数学理论对通讯信道优先级进行评估，按照从高到低的顺序进行逐次恢复，增强了恢复质量，使该方法更加科学可靠。

5 结论

多媒体技术与互联网的广泛应用，使得越来越多的信息需要通过网络进行传输。为确保通讯系统安全运行，必须完善现有的差错检测与篡改恢复技术。本文基于模糊数学理论对被篡改的信息进行恢复。将其应用在密文图像信息的篡改检测，构建有效的数学模型，使篡改恢复问题得到解决。通讯安全问题是一项长期性专业工作，如何使该方法更加合理应用，进一步保证密文安全是下一步工作重点。