卷积神经网络中激活函数的性质分析与改进

张 焕，张 庆，于纪言

(南京理工大学机械工程学院，江苏 南京 210094)

1 引言

深度学习(Deep Learning，DL)[1]是近年来人工智能相关领域最令人瞩目的发展方向，卷积神经网络(Convolutional Neural Networks，CNN)作为深度学习的主力军，已经在安防、交通、医疗、教育、零售、家居等诸多领域特别是图像相关的任务上表现优异[2-6]。卷积神经网络的发展源于人工神经网络(Artificial Neural Network，ANN)[7-9]，且其具备模拟动物的神经元这一生物理论基础。而激活函数(Activation Functions)作为卷积神经网络的一个重要组成部分，其存在的意义重大。

激活函数通常上也可以称为非线性映射层，从数学角度来看，它的引入可以增加卷积神经网络的非线性表达能力。从生物学理论角度来看，激活函数对数据的作用过程模拟了生物神经元对电信号的处理过程。生物神经元通过一定的阈值激活或抑制接收到的电信号而产生一定的输出，从而完成了信息的处理与传播。因此，参考生物神经元，理想的激活函数应该是将输入数据映射为{0，1}两种结果的输出。但是，卷积神经网络模型训练、误差反向传播的过程要求激活函数具备一定的可微性，显然理想“神经元激活”目前不符合文中的模型训练要求。因此，寻找时间、空间及特征采集度高效的激活函数成为了深度学习的一项重要基础研究内容。

在初期的深度学习发展过程中，传统S型非线性饱和激活函数sigmoid和 tanh 函数得到了广泛的应用[10]。随着深度学习理论和计算机运算能力的快速发展，深度学习模型的深度大大提升，此类函数在模型训练过程中导数连乘很容易出现“梯度弥散”的问题[11]。2010年，Hinton教授首次提出了修正线性单元(rectified linear units，relu)[12]作为激活函数，Krizhevsky 等在2012 年 ImageNet ILSVRC 比赛中使用了激活函数ReLU，验证了ReLU激活函数具备稀疏性的优势，能使模型训练以及模型收敛速度大大加快，且很好的解决了sigmoid和tanh函数存在的梯度弥散问题。但是ReLU激活函数在负半轴的梯度恒为零，模型在训练过程可能会发生神经元“坏死”的状况[13]。

为了解决ReLU负半轴置0而导致“神经元坏死”的情况，2012年至今研究者们提出Leaky ReLU[14]、PReLU[15]、Noisy ReLU[16]、ELUs[13]、ReLU-softplus[17]、ReLU-softsign[18]、TReLU[19]、Swish[20]、Xwish[21]，ReLU阈值[22]等激活函数，这些激活函数有效缓减了“神经元坏死”的问题。下文将以神经网络前向传播、反向传播为例，推导激活函数的作用过程，并总结、分析优良激活函数应该具备的特性。基于激活函数的发展及文中有关激活函数性质的分析，本文提出了一种新型激活函数ReLU-XeX，通过理论分析其优越性，并通过数据模型实验证明了其优越性。

2 激活函数的性质分析

激活函数的直观作用是对已有数据进行非线性映射，增加表达能力。在神经网络中，每一层网络所学习到的特征表现为权值的形式更新。从神经科学学科角度来看，其目的是激活某些信号进行表达，且抑制某类信号的表达。以下将推导和分析神经网络模型在训练过程中激活函数的作用，并对激活函数性质进行解释和分析。

可以把神经网络的训练过程分为前向传播和反向传播。其中，前向传播的过程是输入层输入、经过隐藏层的特征提取，最后在输出层进行输出；反向传播是根据输出层的实际输出与目标期望输出通过某种计算公式来计算误差损失，并通过每一层的误差损失求得反向梯度来更新权值参数的过程。图1是一个4层的神经网络，输入层为第0层，中间三个隐藏层，第四层为输出层。图2为激活函数的作用示意图。以下将以图1中的深层神经网络为例，推导分析激活函数在前向传播和反向传播中发挥的作用。

图1 神经网络

图2 激活函数作用示意图

2.1 前向传播

输入信号通过各个网络层的隐节点产生输出的过程称为前向传播。在网络训练过程，前向传播会生成一个标量损失函数。其过程表达式为(1)(2)(3)(4)(5)。其中，x为输入，w[i]、b[i]为第i层的权值参数和偏置，z[i]、a[i]是第i层输入神经元的值和经激活函数激活后神经元的值，g[i]为第i层的激活函数。

第一层需要计算

z[1]=w[1]x+b[1]，a[1]=g[1](z[1])

(1)

第二层需要计算

z[2]=w[2]a[1]+b[2]，a[2]=g[2](z[2])

(2)

第三层需要计算

z[3]=w[3]a[2]+b[3]，a[3]=g[3](z[3])

(3)

第四层需要计算：

z[4]=w[4]a[3]+b[4]，a[4]=g[4](z[4])

(4)

将上述的输入x记作a[0]，前向传播的过程可以写成通式

z[i]=w[i]a[i-1]+b[i]，a[i]=g[i](z[i])

(5)

分析式(1)～(5)，在神经网络前向传播的过程中，输入经过权值和偏置的累加线性映射，得到一个初值，这个初值要经过激活函数的非线性映射进一步加工，以增强网络表达能力。因此分析前向传播过程，激活函数应该具备以下性质：

1)激活函数对数据进行非线性映射从而增加表达能力，因此该过程要求激活函数为非线性函数；

2)激活函数应该符合或近似符合零均值分布条件，以增加其对数据的适应性；

3)激活函数计算的时间、空间复杂度应该尽量较小。

2.2 反向传播

反向传播是根据输出层的实际输出与目标期望输出通过某种计算公式来计算误差损失，并通过每一层的误差损失求其反向梯度来更新权值参数。其过程表达式为(6)、(7)、(8)、(9)、(10)，反向传播过程使用梯度下降法的参数更新公式为式(11)、(12)。其中，将da[j]作为输入，得到da[j-1]、dw[j]、db[j]作为输出，a为学习率，其余参数表达参照2.1节中的前向传播。

dz[j]=da[j]*g[j]′(z[j])

(6)

dw[j]=dz[j]*a[j-1]T

(7)

db[j]=dz[j]

(8)

da[j-1]=(w[j])T*dz[j]

(9)

dz[j-1]=(w[j])T*dz[j]*g[j-1]′(z[j-1])

(10)

w=w[j]-a*(w[j+1])T*dz[j+1]*

g[j]′(z[j]) *a[j-1]T

(11)

b=b-a*db=b[j]-a*(w[j+1])T*

dz[j+1]*g[j]′(z[j])

(12)

分析式子(6)～(12)，可以得出权值参数的更新与激活函数导数值的大小存在线性相关关系，深层神经网络的参数更新中会出现激活函数的导数连乘。因此分析前向传播过程，激活函数应该具备以下性质：

1)要求激活函数的导数不能太小或太大，以避免出现梯度消失或梯度爆炸的问题；

2)要求激活函数的导数不能过多的置“0”，以避免出现“神经元坏死“问题；

3)要求激活函数便于计算机求导计算，优化计算成本及性能[23]，以避免计算量巨大的问题；

4)要求激活函数理论上存在一定的稀疏性，以符合神经科学的研究论证；

5)要求模型刚开始训练的时，激活函数的导数应该较大，加速模型收敛；同时在模型收敛后半段，应要求激活函数有一定的软饱和性，即导数渐渐趋于0，使得模型收敛至最优值；

6)要求最好选择一个正负值都可以输出的激活函数，因参数w的更新方向与该层的输入a[j-1]有关，使得参数的更新方向自由；

7)要求激活函数应该具备一定的饱和性，使得模型对数据噪声具有一定的鲁棒性。

3 改进的激活函数ReLU-XeX

考虑函数f(x)=x*e-|x|，将其命名为XeX。其函数、导数表达式为(13)(14)；其函数、导数图像如图3、图4。从式(13)(14)可以看出，函数XeX具备一些性质：

1)其本身为非线性函数；

2)符合0均值分布；

3)在零点附近其导数较大，能加速模型的收敛；

4)函数输出有正负值，保证了参数更新的方向自由；

5)具有软饱和性，对数据噪声具备一定的鲁棒性。

(13)

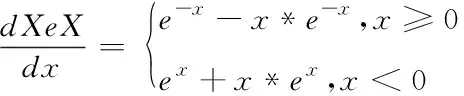
(14)

图3 XeX函数图

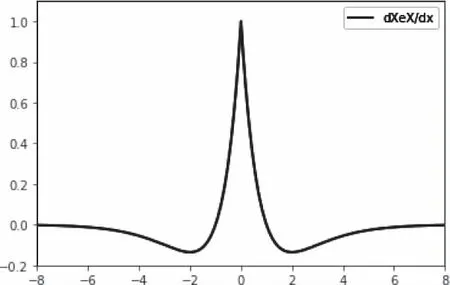
图4 XeX导数图

(15)

(16)

图5 ReLU-XeX函数图

图6 ReLU-XeX导数图

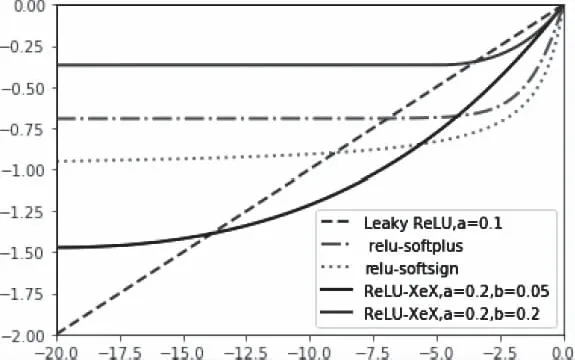
图7 函数图对比

图8 导数图对比

图7、图8为Leaky ReLU(a=0.1)、relu-softplus[13]、relu-softsign[14]以及ReLU-XeX激活函数在负半轴的函数、导数图像。对比图5、6、7、8可以得出：

1)ReLU-XeX相较于Leaky ReLU(a=0.1)，其负半轴斜率先大后小的特性有利于模型加速收敛；

2)ReLU-XeX相较于relu-softplus、relusoftsign，其导数与正半轴导数(导数为1)不连续且相对较小(a控制着其大小)，这使得输入值的正负对权值参数的更新影响更大，增大了输入正负值的区分度；

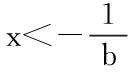
4 仿真结果与分析

为了验证上文提出的ReLU-XeX激活函数的有效性，本文分别在MNIST、CIFAR-10、CIFAR-100、MSTAR四种数据集上，对sigmoid、tanh、ReLU、Leaky ReLU(a=0.1)、relu-softplus、relu-softsign、ReLU-XeX七种激活函数作性能测试。针对四种数据集，文中分别设计了相应的卷积神经网络模型。

目前深度学习有很多成熟的开源框架，如Pytorch、TensorFlow、Caffe、CNTK等等。本实验是在深度学习框架Pytorch下完成的，运行显卡为NVIDIA GeForce GTX 1060，并且使用了CUDA进行加速。本文在Jupyter Notebook下运用matplotlib对实验结果进行了可视化，并对参与实验的几种激活函数展开了性能对比和分析。

4.1 MNIST数据集上的仿真结果及分析

MNIST数据集是用于识别0～9这十种数字的图像数据集，一共包含70000张28*28像素的灰度手写数字图片，其中60000张图像为训练集，10000张图像为测试集，图9为其部分图像样本。

图9 MNIST数据集

图10为针对MNIST数据集设计的卷积神经网络模型；表1为本模型相关的参数及优化方法、损失函数设计。将尺寸为28×28的灰度图像按中心裁剪的方法裁剪成24×24，并对其作归一化处理输入设计好的卷积神经网络模型。三个卷积层的卷积核尺寸都是3×3，卷积步长(stride)为1，卷积填充(padding)为1，每个卷积层后都跟着一个最大池化层。最后将提取的特征图展开为特征向量，由一个全连接层相接。

表2是在该模型在不同激活函数作用下得到的测试集准确率。由表2可知，文中提出的改进激活函数ReLU-XeX在参数a=0.2、b=0.2和a=0.2、b=0.05时均取得了比其它六种激活函数更优的效果。其中在a=0.2、b=0.05时取得了最高准确率99.02%，相较于sigmoid提高8.08%；相较于tanh提高0.73%；相较于ReLU提高0.19%；相较于Leaky ReLU(a=0.1)提高0.09%；相较于relu-softplus提高0.26%；相较于relu-softsign提高0.05%。

图11为30个训练周期，即9000个训练批次得到的该模型在不同激活函数作用下训练集的平均损失与训练批次数的关系，从图中可以看出，relu-softplus、relu-softsign以及本文提出的改进激活函数ReLU-XeX相较于传统激活函数sigmoid、tanh、ReLU、Leaky ReLU，在模型收敛速度上有更大的优势。图12为模型训练初期，模型的60～150批次数训练的平均损失，从图中能看出该模型收敛的先后顺序是ReLU-XeX(a=0.5，b=0.05)、relu-softplus、ReLU-XeX(a=0.2，b=0.05)、relu-softsign、ReLU-XeX(a=0.2，b=0.5)。图13为几种激活函数的导数图像，参考之前得到的结论，权值参数的更新和激活函数导数值的大小成正相关，这种模型收敛的先后顺序得到了论证。

图10 设计的MNIST的CNN模型

表1 MNIST卷积神经网络模型参数设计

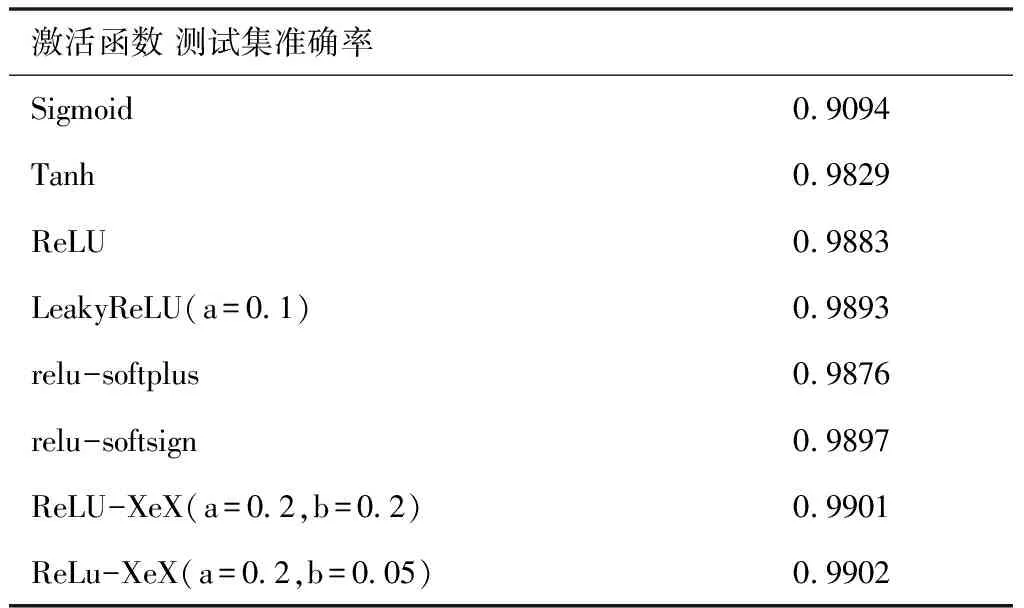
表2 MNIST数据集下的实验结果

图11 各激活函数的模型损失

图12 损失下降对比

图13 导数对比

4.2 CIFAR-10、CIFAR-100、MSTAR数据集上的仿真结果及分析

CIFAR-10是包含10种类别共60000张32*32像素的三通道图像数据集；CIFAR-100是对CIFAR-10更加细致划分而得到的100类图像数据集。它们都是50000张用作训练集，10000张用作测试集，部分数据展示如图14。MSTAR美国国防高等研究计划署(DARPA)推出的开源SAR军事目标图像数据库。本文采用的MSTAR数据集种训练集有2746张图像，测试集有2426张图像，都是128×128分辨率的三通道十类别军事目标图像，部分数据展示如图15。

图14 CIFAR-10/100数据集

图16为针对CIFAR-10/CIFAR-100/MSTAR数据集设计的卷积神经网络模型；表3为模型相关的参数及优化方法、损失函数设计。表4为模型在不同激活函数作用下得到的测试集准确率，从表4中可以看出，激活函数在不同数据集的表现效果不尽相同，这与具体模型的特点以及数据集的特征有关。文中提出的改进激活函数ReLU-XeX在参数a=0.2、b=0.2和a=0.2、b=0.05时整体取得了比其它六种激活函数更优的效果。

图15 MSTAR数据集

图16 CIFAR-10/CIFAR-100/MSTAR卷积神经网络模型

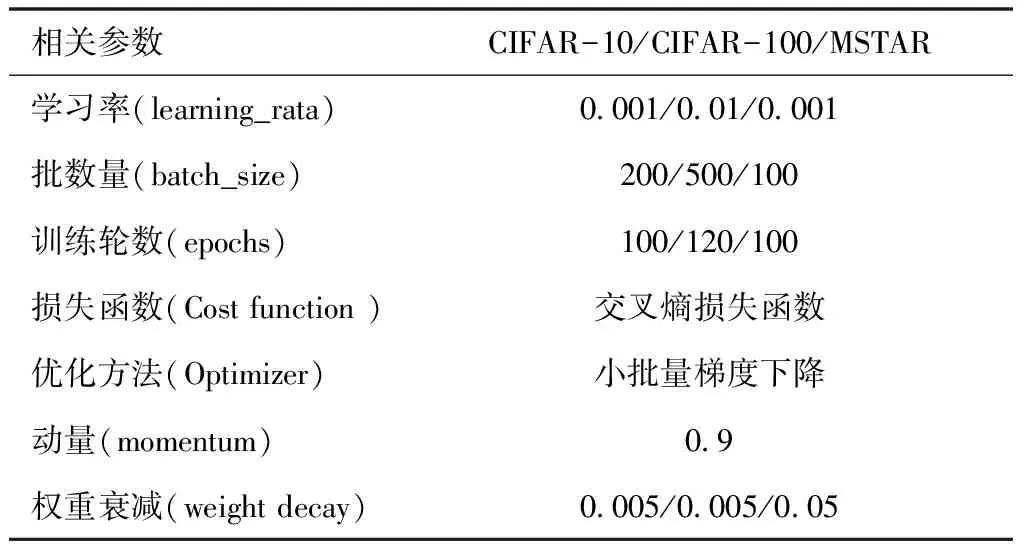
表3 模型参数设计

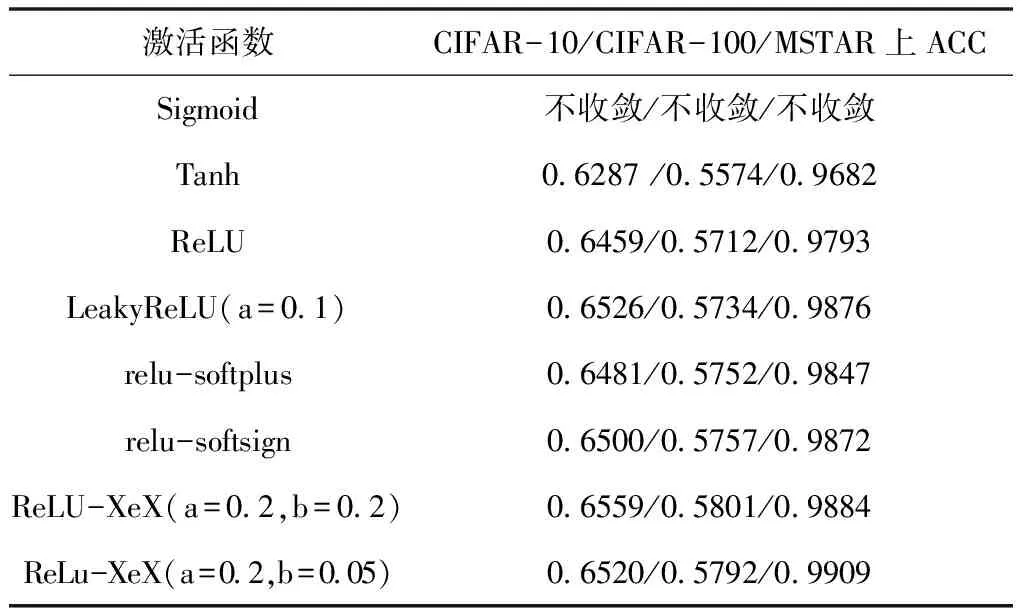
表4 CIFAR-10/CIFAR-100/MSTAR的实验结果

5 结语

上文通过研究激活函数的发展进程，以及在分析神经网络前向传播和反向传播中激活函数所起到的作用的基础上，提出了改进的激活函数ReLU-XeX，有效的缓解了梯度消失、“神经元坏死”等问题。在MNIST、CIFAR-10、CIFAR-100、MSTAR数据集上的仿真结果表明，改进的激活函数ReLU-XeX在本文仿真中整体表现强于其它的一些激活函数，且在模型的收敛速度上有所提升。

实验数据显示，激活函数的表现性能不仅与激活函数本身的性质有关，还和数据集的数据分布、模型复杂度有关。当网络模型足够复杂，类比大脑神经信息传播，此时激活函数理论上也应该要具备很高的稀疏性，以防止过拟合。本文提出的改进的激活函数ReLU-XeX在ReLU的基础上置负半轴软饱和，在模型较为复杂时其理论上可能仍存在稀疏性不足的问题。但深度学习的应用对实时性有很高的要求，也即需要用较简易的模型完成实际任务，本文提出的改进的激活函数ReLU-XeX保留了负半轴的部分信息，提高了简易模型的泛化能力。同时，ReLU-XeX在负半轴达到饱和后，其导数始终为零，减小了离群点对模型的干扰以及增强了模型对噪声的鲁棒性。本文为激活函数的设计改进提供了一种思路，激活函数仍存在许多可以进一步优化改进的地方。