基于MCP正则化SWESN的时间序列预测方法研究
2022-05-14刘半藤尹则高
刘半藤,陈 唯,尹则高,孙 萍
(1. 常州大学信息科学与工程学院,江苏 常州 213164;2. 中国海洋大学水利工程学院,山东 青岛 266003;3. 浙江树人大学信息科技学院,浙江 杭州 310015)
1 引言
时间序列预测指的是通过已知的历史数据去预测未知的未来数据,已经在医学、金融、军事等[1-3]领域中得到了广泛的应用,由于实际生活中的时间序列大多呈现非线性和不稳定性,因此对于非线性和不稳定时间序列的预测问题一直备受各个领域中研究学者的关注[4]。
目前,对于非线性和不稳定时间序列进行预测的主要方法是采用回声状态网络(Echo State Network,ESN)[5]。其特点就是采用被称之为“储备池”的大规模随机稀疏连接网络作为传统神经网络的隐层,去处理非线性和不稳定的时间序列,并且在训练过程中只需训练储备池至输出层的输出权值,简化了网络的训练过程,避免了传统神经网络中存在的易于陷入局部最优、训练算法复杂等问题[6]。目前,一部分学者为了提高ESN的性能,纷纷开始研究改进ESN的方法,主要集中在储备池拓扑结构优化和输出权值优化两个方面[7-8]。在储备池拓扑结构方面,传统ESN的储备池中采用随机网络致使模型训练无目的性,为了解决此问题,李菡[9]等学者提出采用同时具备随机性和规则性的小世界回声状态网络作为ESN的储备池去预测非线性时间序列,提高了预测模型的适应性和预测精度;但以上小世界回声状态网络的节点连接属于确定性连接,对具有时变性和模糊性的时间序列预测精度不高,因此,伦淑娴[10]等学者提出采用改进的小世界回声状态网络作为ESN的储备池,即储备池网络节点间的加边概率根据节点间距离的负指数函数进行修正,缩短了训练时间并提高了对具有时变性和模糊性的非线性时间序列的预测精度。
在输出权值方面,传统ESN的输出权值计算采用伪逆法,但伪逆法求解高维线性回归时易出现共线性问题[11];为了解决此问题,Wang[12-13]等学者提出采用Ridge回归、Lasso回归等线性回归方法计算输出权值,通过添加L2范数、L1范数解决共线性问题,但Ridge回归、Lasso回归对偏大的输出权值施加了更大的惩罚,属于有偏估计,模型预测时容易出现过拟合问题[14]。为了解决以上问题,在计算输出权值时需要采用渐近无偏正则化方法,提高预测模型的预测精度与泛化性能。常见的渐近无偏正则化方法有SCAD(Smoothly Clipped Absolute Deviation)正则化法[15]和MCP(Minimax Concave Penalty)正则化法[16],目前,已有学者将SCAD正则化法成功应用于小世界回声状态网络的输出权值优化中[17],提高了小世界回声状态网络对非线性时间序列的预测精度。但采用MCP正则化法优化小世界回声状态网络输出权值的方法还未曾提出,而且MCP正则化法的惩罚函数具有最小最大凸性,能对偏大或偏小的输出权值做更恰当的惩罚,更适用于处理多维非线性数据[18-19],因此,本文提出了一种基于MCP正则化SWESN的时间序列预测方法(Minimax Concave Penalty-Small World Echo State Network, MCP-SWESN),提高小世界回声状态网络对非线性时间序列的预测能力。
2 基于MCP正则化SWESN的时间序列预测方法
本文采用改进的小世界网络作为储备池,得到小世界回声状态网络(Small World Echo State Network,SWESN)。其拓扑结构如图1所示。

图1 小世界回声状态网络拓扑图
小世界回声状态网络的状态方程和输出方程分别为
x(t)=f(Winu(t)+Wxx(t-1))
(1)
y(t)=xT(t)Wout
(2)
其中,u(t)∈RL、x(t)∈RM和y(t)∈R分别表示储备池t时刻的输入变量、状态变量和输出变量;激活函数f通常取双曲正切tanh函数;Win∈RM×L、Wx∈RM×M和Wout∈RM分别为输入权值矩阵、储备池内部权值矩阵和输出权值矩阵。输入权值矩阵Win随机生成,确定后不再改变。
改进的小世界网络中储备池内部权值矩阵Wx通过建立加边概率与节点间距离的函数关系式获得,确定后不再改变。加边概率P值随着节点间的距离增大按指数方式递减,即:
P=α×e(-β×d)
(3)
其中,P取值范围为[0, 1],表示节点间的连接权值。d表示节点间的欧氏距离,α用来调节距离灵敏度,β用来调整网络的整体密度。
输出权值矩阵Wout在训练时获得,即最小化目标函数对应的Wout值,如式(4)所示,并通过最小二乘法求解获得,如式(5)所示:
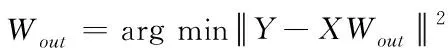
(4)
Wout=X†Y=(XTX)-1XTY
(5)
其中,(X,Y)是训练样本,X†是X的伪逆。
正则化方法是在最小化目标函数的基础上添加惩罚函数,最小化添加惩罚项的目标函数对应的Wout估计值如式(6)所示:
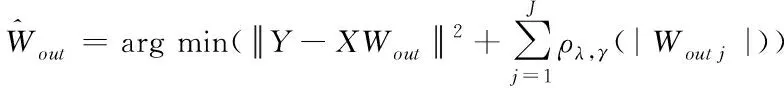
(6)
其中,J表示变量个数,ρλ,γ表示罚函数。
本文采用最小最大凹罚(MCP)作为惩罚函数,MCP罚函数在原点产生奇异值,能够产生稀疏解。并且,在|θ|>γλ时,直接将变量置为零,满足对变量θ的近似无偏估计,MCP罚函数如式(7)所示
(7)
其中,γ,λ为可调超参数(γ>2,λ>0),采用遍历手段获得,θ为参数向量,本文中为输出权值Wout。
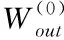

(8)
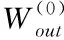
out=arg min(‖Y-XWout‖2+

(9)
其中,D为Wout中非零元素个数,通过对式(9)重复执行Ridge回归解可得输出权值估计
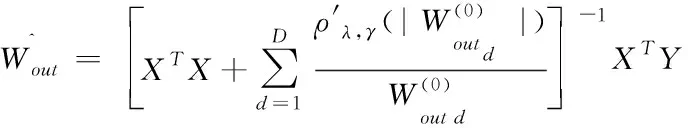
(10)
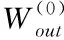
3 仿真研究
3.1 测试数据
为了验证本方法的有效性,分别用Lorenz混沌时间序列、Mackey-Glass混沌时间序列和实际的PM2.5浓度时间序列进行测试。
1)Lorenz混沌时间序列生成方法如下
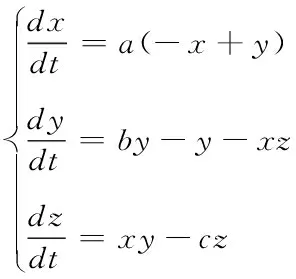
(11)
取a=10,b=28,c=8/3,x(0)=12,y(0)=2,z(0)=9,系统呈现混沌特性。利用四阶龙格库塔算法对Lorenz系统求得1000个时刻作为测试数据。
2)Mackey-Glass混沌时间序列生成方法如下
(12)
取a=0.2,b=0.1,c=10,τ=17,x(0)=1.2,t(0)=0,系统呈现混沌特性。利用四阶龙格库塔算法对Mackey-Glass系统求得1000个时刻作为测试数据。
3)实际时间序列采用北京市某年度的PM2.5浓度时间序列,数据来源为中国空气质量在线监测分析平台(https:∥www.aqistudy.cn/)。
3.2 仿真分析
通过将Lorenz混沌时间序列、Mackey-Glass混沌时间序列和实际PM2.5浓度时间序列归一化、相空间重构处理后进行仿真测试和分析,分别取前500个时刻进行训练,而后200个时刻进行预测,测试结果进行反归一化。MCP-SWESN对Lorenz混沌时间序列、Mackey-Glass混沌时间序列和北京市某年度的PM2.5浓度时间序列的预测结果如图2-图4所示。

图2 MCP-SWESN对Lorenz序列预测结果

图3 MCP-SWESN对Mackey-Glass序列预测结果

图4 MCP-SWESN对实际PM2.5浓度序列预测结果
图2-图4表明MCP-SWESN对Lorenz混沌时间序列、Mackey-Glass混沌时间序列和实际PM2.5浓度时间序列的预测均与实际曲线走势一致,结果吻合度较好。
储备池规模会影响ESN及其改进方法的预测结果,因此为进一步分析预测误差,需要比较不同规模储备池的ESN、SWESN、Ridge-SWESN、Lasso-SWESN、SCAD-SWESN和MCP-SWESN对Lorenz混沌时间序列、Mackey-Glass混沌时间序列和实际PM2.5浓度时间序列的预测结果,并采用标准均方根误差(NRMSE)作为全部仿真预测的性能指标

(13)
其中,Q表示预测时间序列长度,Yd(t)表示目标值,Y(t)表示预测值。avg(Yd(t))表示目标值均值。
采用上述ESN及其改进的六种方法分别对三组时间序列进行仿真,重复30次,误差结果取平均值。预测Lorenz混沌时间序列、Mackey-Glass混沌时间序列和实际PM2.5浓度时间序列的训练NRMSE、测试NRMSE结果分别如图5-图10所示。选择最合适的储备池规模所对应的预测结果,结果如表1-表3所示。
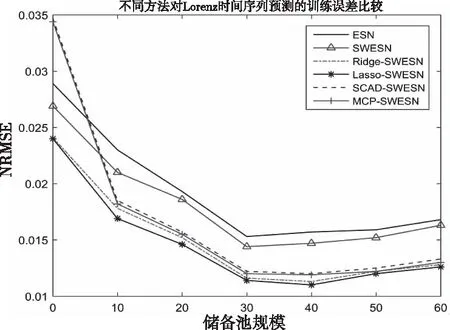
图5 不同方法的训练误差结果(Lorenz)

图6 不同方法的测试误差结果(Lorenz)
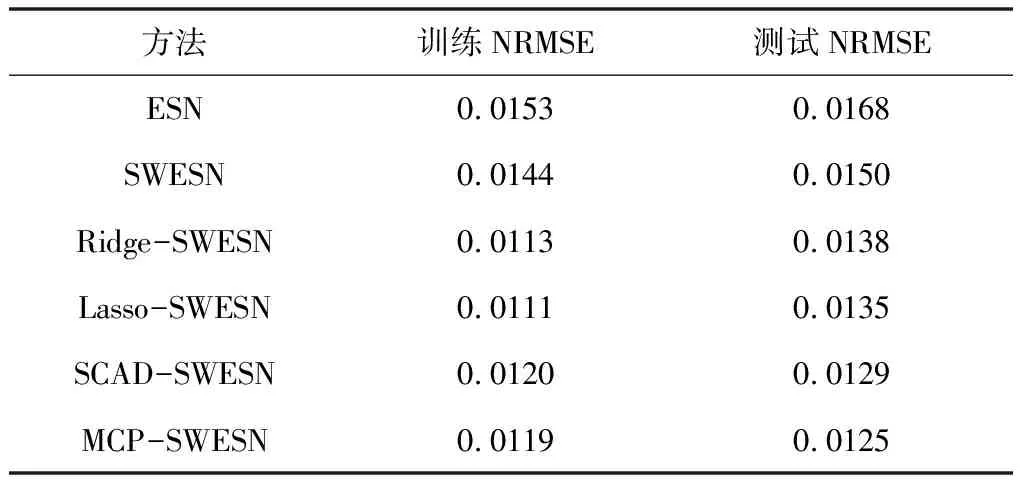
表1 Lorenz混沌时间序列预测结果对比
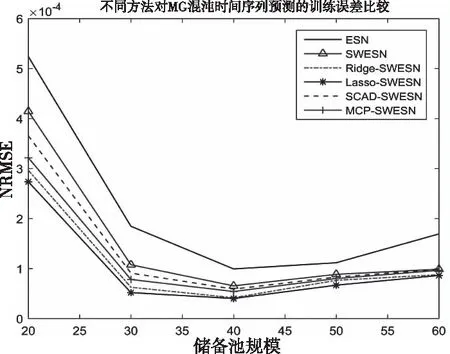
图7 不同方法的训练误差结果(Mackey-Glass)

图8 不同方法的测试误差结果(Mackey-Glass)

表2 MG混沌时间序列预测结果对比

图9 不同方法的训练误差结果(PM2.5)

图10 不同方法的训练误差结果(PM2.5)

表3 实际PM2.5浓度时间序列预测结果对比
上述图表展示了不同储备池规模下,ESN、SWESN、Ridge-SWESN、Lasso-SWESN、SCAD-SWESN和MCP-SWESN六种预测方法对Lorenz混沌时间序列、Mackey-Glass混沌时间序列和实际PM2.5浓度时间序列进行预测的训练NRMSE和测试NRMSE情况。MCP-SWESN方法在对上述三种时间序列进行预测时测试NRMSE在六种模型中最小,预测精度最高;相比于ESN、SWESN和SCAD-SWESN方法,MCP-SWESN方法的训练NRMSE和测试NRMSE均较小,说明MCP-SWESN预测方法的非线性拟合能力有了一定的提升;同时,相比于Ridge-SWESN、Lasso-SWESN预测方法,MCP-SWESN方法的训练NRMSE和测试NRMSE相近,说明MCP-SWESN方法很好的解决了Ridge-SWESN和Lasso-SWESN预测模型出现的过拟合问题。
4 结语
本文提出一种基于MCP正则化SWESN的时间序列预测方法,采用改进的小世界回声状态网络,缩短模型的训练时间并提高预测精度;采用MCP正则化方法优化改进的小世界回声状态网络的输出权值,解决常规回归方法计算权值时出现的过拟合问题,提高预测模型的非线性拟合能力。最后,仿真实现ESN、SWESN、Ridge-SWESN、Lasso-SWESN、SCAD-SWESN和MCP-SWESN六种预测方法对Lorenz混沌时间序列、Mackey-Glass混沌时间序列和北京市某年度的PM2.5浓度时间序列的预测,结果显示:基于MCP-SWESN的时间序列预测方法具有更强的预测能力。
