三轴气浮台的自动平衡系统研究

陈志明，骆州淮，吴云华

(南京航空航天大学航天学院，江苏 南京 210016)

1 引言

三轴气浮台的重心和旋转中心不重合会造成一个不平衡力矩，这个不平衡力矩的存在会影响气浮台的正常使用[1]。为了保证气浮台可以消除外部干扰以及台体本身的配平误差，需要引入自动平衡系统进行气浮台的自动配平。自动平衡系统由控制器及滑块滑轨组成，通过姿态测量系统进行平台运动状态检测，同时由控制器对滑块进行调节直至气浮平台进入稳定平衡状态。

由于手动调平的精度不高，而且非常费时，因此利用自动平衡来减小不平衡力矩一直是许多科研单位的研究重点。文献[2]首先对气浮台进行了动力学建模，然后通过引入倾斜力矩来补偿惯性坐标系下常值干扰力矩，从而实现气浮台的自动平衡；文献[3]通过复摆模型结合台体自然平衡角度的方法来计算台体固有质心偏移的静态计算方法，进而研制了三轴气浮台的自动平衡系统；文献[4]对重力引起的不平衡力矩进行了分析，得到了重力梯度不平衡力矩是气浮台台体二倍倾斜角的正弦函数的结论；文献[5]详细的介绍了三轴气浮台的动力学建模过程，分析了气浮台浮起部分的角度与角速度变化周期与偏心距的关系，自动平衡可以在十几分钟内完成。

为了使气浮台在后续的飞轮控制和冷气控制中都达到设计的精度，需要补偿不平衡力矩。本文在充分考虑工程的实用性后，结合复摆模型，设计了一种简便实用的自动调平衡方法。

2 三轴气浮台调平衡总体方案

2.1 总体方案设计

鉴于自动调节平衡的调节范围小，本文首先对气浮台进行手动粗配平，再采用自动精调平。手动配平又分为两个步骤，首先在气浮台底部设计的3个凹槽内增减质量块的个数，使气浮台浮起部分进行有规律的复摆运动。然后根据气浮台台体复摆周期估计气浮台体偏心距大小，通过手动调节质量块补偿干扰力矩，实现手动粗配平。

在手动粗配平的基础上采用自动配平，自动配平系统根据估计的偏心距，计算补偿重力不平衡力矩所需要滑块的移动量，通过伺服电机驱动相应的质量块对偏心距进行补偿，从而完成自动配平[6]。其中，轴气浮台调平衡总体流程如图1所示。

2.2 气浮台台体结构与坐标系定义

在气浮台的旋转中心建立与气浮台一起转动的机体坐标系和相对地球静止的惯性坐标系。假设初始时刻两个坐标系重合，当给定一组姿态欧拉角时，气浮台可以绕欧拉轴转动，来确定平台的唯一方位[7-9]。气浮台的实际台体坐标系和欧拉角变化示意如图2所示，其中ψ为偏航角，θ为俯仰角，φ为横滚角。

2.3 三轴气浮台手动调平衡

首先通过人工调平经验，在气浮台底部设计的3个凹槽内增减质量块的个数，对气浮台进行初步调平，从而保证气浮台不会倒向一边。此时气浮台的重心已经调节至旋转中心以下，气浮台浮起部分有规律的绕旋转中心摆动，气浮台此时的运动可以视为复摆运动[10-12]。

然后通过人工测得气浮台的摆动周期，利用摆动周期来估计不平衡力矩和偏心距，通过手动移动滑轨上的质量块实现对气浮台的手动粗调平。当偏心距与不平衡力矩满足自动平衡条件时，手动调平结束，进入自动调平阶段。

2.4 三轴气浮台自动调平衡

三轴气浮台上共装有3个自动平衡装置，通过控制信号驱动步进电机从而带动质量块移动。3个自动平衡装置分别可以补偿x，y，z轴上的偏心距。其中自动平衡装置在气浮台上的实际装配如图3和图4所示。

图4 X、Y轴自动平衡装置装配示意图

首先通过陀螺测得气浮台的实时角速度，然后通过计算角速度的变化周期，得到气浮台浮起部分的摆动周期。

为了节省调平时间，本文采用非线性曲线拟合函数的方法计算气浮台浮起部分的摆动周期。首先，采集20秒的角速度数据，然后通过数据拟合正弦函数，最后算得气浮台的摆动周期。

在计算得到摆动周期后，通过复摆周期公式反算偏心距，然后驱动步进电机，移动质量块。

其中复摆周期公式为

(1)

其中T为复摆周期，m为气浮台浮起部分质量，I为转动惯量，roff为偏心距。

偏心距在各个轴上的分量如图5所示，其中a，b为形成的夹角角度。

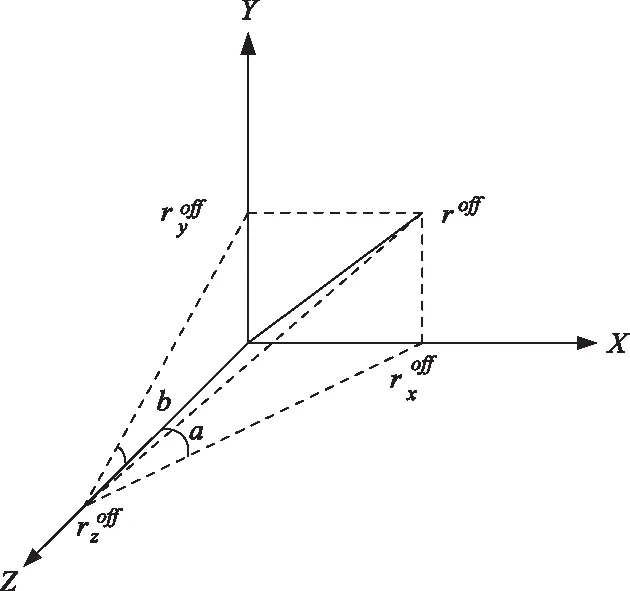
图5 各轴偏心距示意图

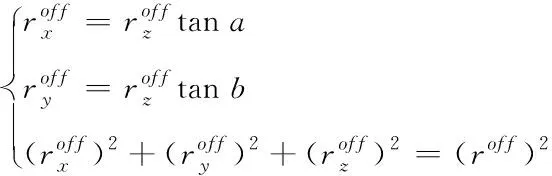
(2)

质量块的移动距离为

(3)

通过式(1)和式(2)可以估计估算偏心距与干扰力矩，如表1所示。

表1 复摆周期与偏心距关系表

3 自动调平衡算法设计

3.1 三轴气浮台动力学建模

三轴气浮台绕欧拉轴转动的方法共有12种，本文采用3-2-1的顺序依次转动[13]。

绕Z轴转动ψ角度的变换矩阵为

(4)

绕Y轴转动θ角度的变换矩阵为

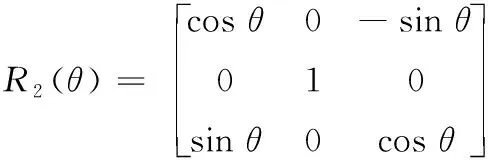
(5)

绕X轴转动φ角度的变换矩阵为

(6)

因此，从惯性坐标系到机体坐标系的姿态变换矩阵可以表示为

C=R1(φ)R2(θ)R3(ψ)

(7)

A=sinφsinθB=cosφcosψD=cosφsinψ

E=sinφcosψF=sinφsinψ

从而旋转欧拉角速度可表示为

(8)

三轴气浮台浮起时的运动状态

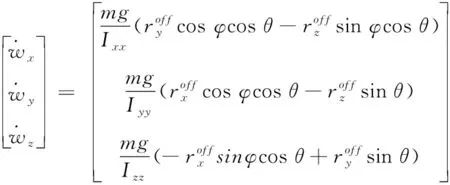
(9)

3.2 仿真结果与分析

首先设置气浮台浮起部分的初始倾角与各轴偏心距，并算出对应的不平衡力矩。然后在Simulink里模拟气浮台的运动状态，得到的气浮台浮起部分的角速度与角度变化周期。实物气浮台的参数见表2所示，动力学模型的仿真初始条件与仿真结果以及在相同条件下在动力学模型中仿真得到的周期与在复摆模型中计算得到的周期误差对比如表3所示。

表2 实物气浮台参数表

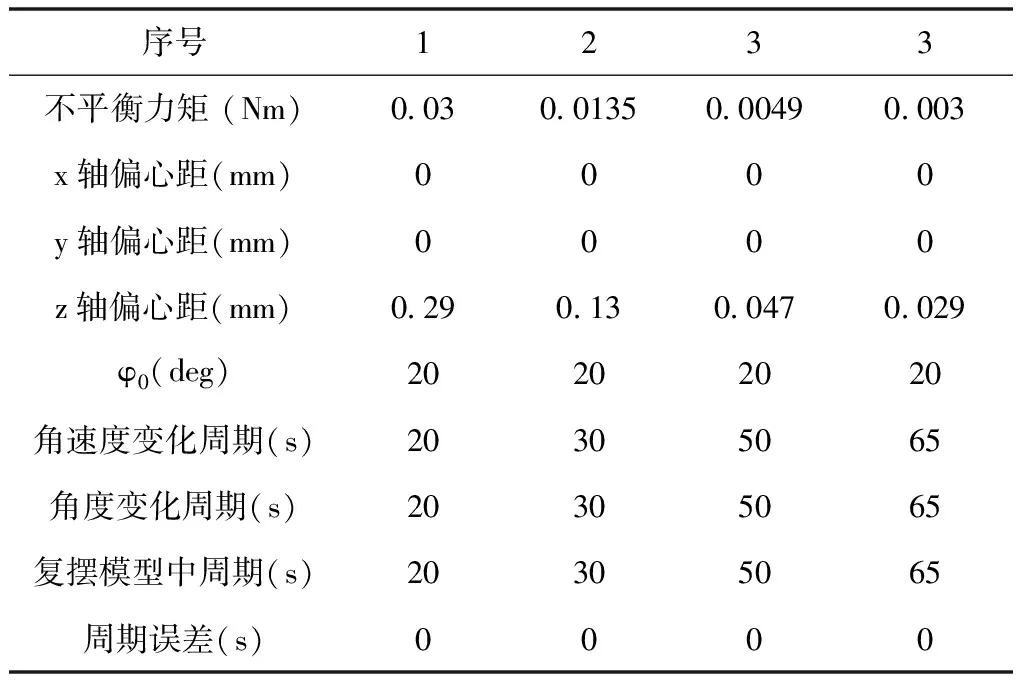
表3 动力学仿真结果与周期误差表

通过对表3数据的分析，可以得到以下结论：当气浮台受到的不平衡力矩越小时，平台的角速度变化周期越长、角度变化幅度越小。由此可通过计算平台的角速度和角度变化周期来确定偏心距与不平衡力矩。

在相同条件下复摆公式算出的周期与动力学模型得到的周期相同，从而验证了通过复摆模型进行自动调平衡的可行性。

4 自动平衡装置设计

本文设计了如图6所示的自动平衡装置，选用FAULHABER 2232S024BX4 SC型步进电机，该电机可实现3000脉冲旋转1圈，具有控制精度高的优点，并且在电机行程上安装了三个光电传感器，用于限位。

图6 自动平衡装置实物图

自动平衡装置的调平精度取决于质量块质量、丝杆螺距、步进电机的转动精度和丝杆有效导程。不同的丝杆螺距对应不同的调平精度，如表4所示。

表4 丝杆螺距与调平精度关系表

在表4的基础上，本文选择丝杆螺距为1mm，质量块质量为0.4kg的步进电机，进而可以总结自动平衡调节性能的参数如表5所示。

表5 自动平衡调节性能参数表

5 实验及测试结果

在手动配平后，气浮台浮起部分摆动周期在20s以上。进入自动平衡阶段后，计算机首先根据陀螺测得的角速度数据算出周期，从而算得偏心距在每个轴上的分量，最后驱动步进电机从而使滑轨上的质量块移动。

气浮台的调平衡实验结果如图7所示，自动平衡装置上的质量块在经过几次移动后，气浮台浮起部分摆动周期达到65s以上。气浮台受到的不平衡力矩控制在3×10-3Nm，此时自动配平结束，总的调平时间小于250s。

图7 自动调平衡实验结果图

由于自动平衡装置的丝杆存在最小刻度误差，大约为0.03mm。将这个最小刻度误差带入复摆周期公式，可以算出周期约为65s。对比实验最后的周期结果，可以得到此时气浮台已经完成了配平。

6 结束语

经过调平后，气浮台浮起部分的摆动周期稳定在65s以上，干扰力矩被控制在了3×10-3N·m以内。在此基础上可以用于开展相关的姿态控制实验。总调平时间可以控制在250s以内，方法简单而且节省时间。

本文首先分析了设计需求，然后进行了气浮台调平衡总体方案设计，在此基础上进行了指标分析计算。所设计的自动平衡系统可以满足三轴气浮台系统的使用要求。