基于随机共振的FHN神经元并联阵列图像复原
2022-05-14张化戈马玉梅潘振宽
张化戈,马玉梅,潘振宽
(青岛大学计算机科学技术学院,山东 青岛 266071)
1 引言
1981年,Benzi等人首先提出了随机共振(SR)概念[1,2],以解释古代气象学中冰川期和与暖气候期周期性交替现象。随着非线性动力学的迅速发展,研究人员发现对噪声的处理不仅可以抑制或消除噪声,而且可以使用噪声来增强信号。
1991年,Longtin等人[3]利用理论模型对整数倍放电节律现象进行了模拟和研究,并推断此节律与随机共振效应有关,这是首次把神经元放电和随机共振效应联系起来。1995年,Collins[4]在研究生物兴奋神经模型时发现了随机共振效应,并提出了非周期性随机共振的概念用来描述FHN中的随机共振现象。这是随机共振和信息论相结合的标志,扩大了随机共振的广度。赵燕等人[5]发现非高斯噪声的存在缩短了FHN神经元的静息态和激发态之间的转换时间,加快了单个神经元的放电节律,表明非高斯噪声在将信息传递到神经元中起积极作用。Tessone等人[6]研究了扩展的FHN模型系统,发现非均质耦合的独特形式导致输出SNR的增加。
近年来,并联阵列方法在SR研究中取得了良好的效果。1995年,Linder等人[7]提出了阵列SR的理论,使用阵列SR可以提高输出信噪比。Wang等人[8]研究了并联双稳态系统,发现并联双稳态系统可以检测到较低输入信噪比下的摄动特征信号。Duan等人[9]提出了基于阈值的并联阵列模型和饱和并联阵列模型。文献[10]通过引入阵列随机共提高了有色噪声下逻辑随机共振的可靠性和鲁棒性。
随机共振现象在许多科学领域都普遍存在,包括化学领域的Belousov-Zhabotinsky反应[11]、生物学中的神经细胞[12]、物理学中的液晶和光学系统[13]等等。在图像处理领域,传统的图像复原方法(如滤波)主要集中在抑制和减少噪声[14],在去除噪声的同时会丢失一些图像信息。随着非线性动力学的发展,随机共振在图像处理领域发挥了重要作用。逐渐涌出了各种基于随机共振的图像处理方法,如使用双边滤波与随机共振相结合去除图像噪声[15];使用动态随机共振增强暗图像[16];通过随机共振神经元模型来增强MR图像[17];使用随机共振进行水印提取[18];通过自适应调整双稳态系统参数,以达到复原图像的目的[19]。但是,这些方法在强噪声环境下取得的效果并不理想。本文提出一种基于随机共振的FitzHugh-Naguma神经元并联阵列图像复原方法。该方法通过行或列扫描方法将2D图像信号转换为1D信号,然后通过脉冲幅度调制将该1D信号转换为1D二进制非周期性信号。再把1D二进制非周期信号作为输入信号通入FHN阵列系统进行处理,最后对输出复原图像。本文的主要工作如下:①结合FHN神经元和阵列SR,建立了基于FHN神经元的阵列SR图像复原模型。②本文将FHN神经元方法与传统滤波方法及二维随机共振方法进行对比。结果表明,该方法在复原图像的视觉方面和PSNR性能方面效果较好,尤其是在低PSNR环境下,对强噪声污染的图像的复原效果较好。
2 系统模型与性能评价
2.1 系统模型设计
在随机共振实验中,大多使用由Langevin方程描述的双稳态系统。该系统在一维信号处理中可以由Fokker-Planck方程表示系统输出随着时间的变化能取得较好的效果。但在二维随机共振实验中由于像素点的空间性,Fokker-Planck在空间方面有着局限性。神经元具有阈值性,是典型的非线性系统。而且在神经元内外部都有噪声的存在,满足了发生随机共振的要求。综上所述该模型有着以下优点:
相对于传统随机共振模型,该方法将阵列随机共振与FHN神经元相结合,充分使用了噪声会引起神经元动力学特性改变的性质,增强了神经元敏感性,提高模型的随机共振性能。经过实验证明:并联FHN神经元系统在图像复原方面取得显著效果。
在图像处理过程中,由加性噪声引起的一般图像退化模型可以如下描述
f(i,j)=s(i,j)+ξ(i,j)for1≤i≤M,1≤j≤N
(1)
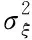
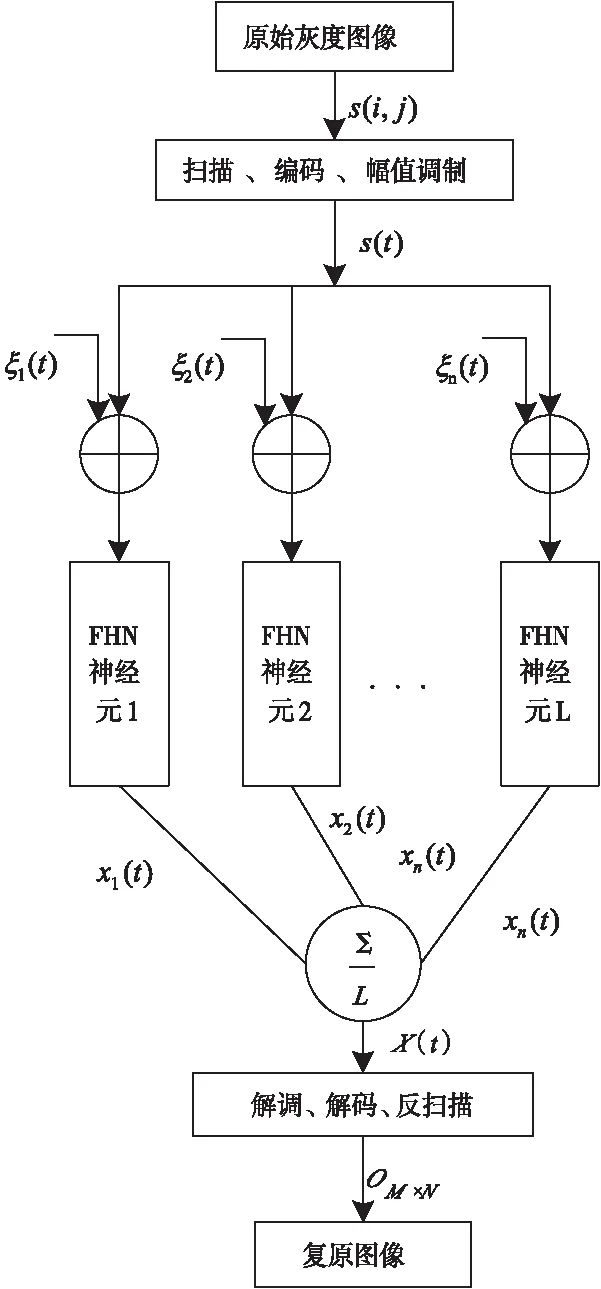
图1 阵列FHN神经元随机共振图像复原流程图
1)原始图像处理
灰度图像每个像素在0到255之间,共有256个灰度值,相较于二值图像可以显示更多的图像信息,但是处理起来更复杂。需要对每个像素点进行处理,首先,通过行或列定向扫描方法对原始灰度图像进行降维处理,使二维图像变成长度为M×N的一维图像序列H1×MN(M和N是原始灰度图像的行和列)。接下来将一维图像序列H1×MN通过二进制编码编码为由0和1组成的且长度为8×M×N的八位二进制序列Q1×8MN。
2)调制
接下来,对二进制序列Q1×8MN进行脉冲幅值调制(BPAM)处理[20],获得一维双极非周期BPAM信号s(t)。

(2)
在式(3)中,A是信号s(t)的扫描电平,G是周期为Tb的矩形脉冲。当t∈(0,Tb)时G(t)=1,否则G(t)=0。Wl(l=1,2,…,8MN)是通过对二进制符号Q1×8MN(0→-1,1→1)进行极性转换而获得的值为-1和1的一维序列。k表示图像的大小,即图像的大小为2k×2k。
3)阵列随机共振处理
为了提高噪声图像的性能,采用FHN并联阵列模型来对退化图像进行处理,本文使用FHN神经元模型,每个SR阵列单元都是FHN神经元,二维FHN模型如下
(3)
v代表快变膜电压变量,0 (4) ξ(t)为高斯白噪声,将一维FHN模型作为并联阵列的阵列单元有下面方程 (5) 在方程(5)中,i=1,2,…,L,L是阵列的大小,h(t)=s(t)+ξn(t)(n=1,2,3,…L)为FHN阵列模型的输入,经过L个FHN系统单元处理后得到xn(t),然后对xn(t)进行算术平均和处理,最后FHN并联阵列系统的输出为X(t) (6) 4)解调 每个新信号Wl从时间tk=kTb开始,持续时间为Tb,二进制非周期信号s(t)的符号间隔为Tb,最优解调方案如下 (7) 5)解码和复原图像 将解调后的二进制一维信号Y1×8MN通过解码和进制转换转变为十进制一维信号Q1×MN,然后通过行列反扫描将Q1×MN转变为二维复原图像OM×N。 在图像处理中,使用PSNR作为一种评价图像的客观标准。它的定义如下 (8) 其中,MSE是原图像与处理图像之间均方误差,定义如下 (9) 其中,M和N表示灰度图像的二维矩阵的行和列,s(i,j)为原始图像像素点的灰度值,o(i,j)为复原图像像素点的灰度值。一般来说,PSNR值越大图像复原效果越好。 为了检测FHN神经元并联阵列对图像的复原效果,采用维纳滤波、均值滤波和二维随机共振方法进行实验比较。二维随机共振方法为:原始噪声图像信号经过行(列)扫描方法得到一维信号后直接通入单个FHN神经元进行随机共振,将输出一维信号通过行列反扫描还原为二维图像,此还原图像为一维随机共振图像。然后对一维随机共振图像进列(行)扫描后通入单个FHN神经元再次进行随机共振,最终输出信号反扫描得到的复原图像为二维随机共振图像。维纳滤波使用MATLAB的现有Wiener2函数,均值滤波使用3×3的模板大小,并用不同大小的FHN神经元并联阵列处理三个不同尺寸的低PSNR灰度图像(128×128、256×256、512×512)。 在FHN并联阵列中,经过查阅参考文献和大量的实验选取,确定γ=10-4,a=0.5和b=1作为阵列FHN神经元的实验参数。实验变量为阵列L的大小。 3.1.1 房屋图像 选择房屋图像的图像像素大小为128×128,然后向房屋图像添加零均值且方差为0.6的归一化高斯白噪声,噪声房屋图像PSNR=7.6193 dB。 图2显示了两种经典滤波方法和二维随机共振方法与FHN神经元并联阵列方法的对比。图2(3)-(5)分别为两种经典滤波和二维随机共振对噪声图像的复原,可见在低PSNR环境下,图像复原效果差,不能很好地还原原始房屋图像。图2(6)-(9)显示了FHN神经元的并联阵列在低PSNR下对噪声房屋图像的复原效果。结果表明,随着阵列大小的增大,随机共振效果和图像复原效果逐步提高,L=10时复原的房屋图像与原始房屋图像几乎相同。 表1为两种经典滤波方法和二维随机共振方法与FHN神经元并联阵列方法复原图像的PSNR性能的比较。从表1中可以看出,两种经典滤波方法和二维随机共振方法的PSNR值较小,复原效果差。 当阵列大小为L=1时,FHN神经元并联阵列SR方法的PSNR值与三种对比方法的PSNR值相似,但复原图像视觉效果明显优于三种对比方法。随着阵列大小L增大,PSNR也逐渐增大,并且当阵列大小L=10时,PSNR = 35.7975dB。 图2 噪声房屋图像通过不同方法得到的复原图像 表1 噪声房屋图像不同复原方法得到的复原图像的PSNR 3.1.2 大米图像 选择大米图像的像素大小为256×256,将零均值且方差为0.4的归一化高斯白噪声添加到大米图像,噪声大米图像PSNR=8.2193dB。 图3显示了两种经典滤波方法和二维随机共振方法与FHN神经元并联阵列方法的对比。 结果表明,随着阵列大小的增大,随机共振效果和图像复原效果逐步提高。 图3 噪声大米图像通过不同方法得到的复原图像 表2 噪声大米图像不同复原方法得到的复原图像的PSNR 表2为两种滤波方法和二维随机共振方法与FHN神经元并联阵列方法复原图像的PSNR性能的比较。从表2中可以看出,当阵列的大小L=10时,PSNR =36.0811dB。比L=1的PSNR值高了约19dB。可以看出,这与SR的非线性性质是一致的,随机共振效应将噪声信号转换为能量信号。 3.1.3 爱因斯坦图像 选择爱因斯坦图像的像素大小为512×512,然后将零均值且方差为0.8的归一化高斯白噪声添加到噪声图像,噪声爱因斯坦图像PSNR=7.4014dB。 图4 噪声爱因斯坦图像通过不同方法得到的复原图像 图4显示了两种经典滤波方法和二维随机共振方法与FHN神经元并联阵列方法的对比。结果表明,随着阵列大小的增大,随机共振效果和图像复原效果逐步提高。但是,在相同大小的FHN神经元并联阵列情况下,爱因斯坦图像的复原效果不如房屋图像和大米图像的复原效果好。这表明,随着图像像素尺寸和噪声强度的增加,噪声图像的复原效果也会受到影响。随着阵列大小的增加,复原图像的效果几乎可以和原始图像相当,但是,计算复杂度也随之增加。处理图像所需的时间也将增加。 所以需要在计算复杂度和图像复原效果之间衡量选择最合适的FHN并联阵列的大小。 表3为两种经典滤波方法和二维随机共振方法与FHN神经元并联阵列方法复原图像的PSNR性能的比较。从表3中可以看出,随着阵列大小L增大,PSNR也逐渐增大,当阵列大小L=10时,PSNR=34.9538dB,比L=1的PSNR值高了约21dB。PSNR值显著增高。 表3 噪声爱因斯坦图像不同复原方法得到的复原图像的PSNR 为了进一步分析FHN阵列SR对图像的复原效果,对模型输出做误码率分析。误码率是最常用的数据通信传输质量指标。计算公式为 (10) 其中RN是错误比特数,TN是总比特数。图5展示了房屋图像(128×128)在不同大小的FHN阵列的输出信号的误码率随噪声强度变化的曲线。在图5中可以看出FHN阵列的大小对误码率的影响非常明显,随着FHN神经元并联阵列的增大,误码率明显降低,所以增加FHN神经元并联阵列的大小有助于减小误码率,使输出信号的正确率增加。 图4 不同大小的FHN阵列的误码率 在本论文中,为了增强低PSNR环境下加噪图像传输质量,提出了一种基于SR的FHN神经元并联阵列灰度图像复原方法。研究结果表明,该方法相对于传统滤波方法和二维随机共振方法,能显著提高复原图像的灰度层次感,提高复原图像的PSNR值并且随着FHN神经元并联阵列大小增加,图像复原效果越显著。本文方法对三种不同像素大小的噪声图像(房屋图像,大米图像和爱因斯坦图像)进行图像复原处理,处理后图像的视觉效果和PSNR性能有明显的提升。本文提出的方法在遥感探测,传输系统,物体检测等方面有着良好的应用前景。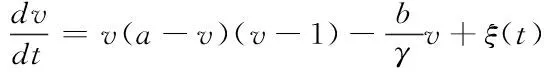


2.2 性能评价

3 实验结果与分析
3.1 实验结








3.2 误码率分析


4 结束语
