全卷积深度学习网络的细胞显微图像分割

夏 平，王 塽，胡 蓉，雷帮军

(1. 三峡大学水电工程智能视觉监测湖北省重点实验室，湖北 宜昌 443002；2. 三峡大学计算机与信息学院，湖北 宜昌 443002)

1 引言

医学细胞显微图像处理是生物医学识别领域中重要的研究课题[1]。随着生物医学技术的发展，对细胞显微图像的研究由定性分析逐渐向结构定量化阶段演进，细胞图像的定量处理正是解决这一问题的方法和手段[2，3]；在此过程中，细胞显微图像分割与识别是判断细胞形态异常及细胞定量研究的前提和基础，通过对细胞层面的定量研究，揭示生物疾病的发病机制、发病原因，发掘产生疾病过程中功能代谢变化[4，5]。细胞图像具有复杂的纹理特征，大小不一、形态各异；同时，细胞的随机分布在显微镜下会形成细胞重叠或粘连，导致显微成像存在边界丢失、模糊、不均匀等特点；传统的分割方法有阈值法[6]、边缘检测法[7]等。近年来，基于多尺度几何分析[8]、水平集[9]、神经网络[11，12]、以及深度学习[10]等理论与方法应用于细胞图像的分割中，取得了较好的分割效果。深度学习[13，14]是基于多隐层的神经网络，具有优异的特征学习能力，能从不同的抽象层次自动学习特征，具有学习更复杂特征的能力，实现对数据更本质的刻画；在此过程中， Ronneberger等提出了U-Net深度学习网络结构[15]，该网络由一个收缩网络及一个对称的扩张网络组成，形成U型结构；收缩网络用于捕获分割图像高维特征信息，扩张网络逐渐恢复图像的细节信息及空间位置信息；扩张网络每次输出获取的图像特征与相应的收缩网络获取的特征合并，进行边界信息补全，以精准定位图像分割区域；该网络已在生物医学图像分割中表现出良好的性能，研究者们在U-net网络结构基础上，针对处理的医学图像提出自己的改进分割算法，并取得了优良的分割效果[16-19]。

针对细胞显微图像的特点，本文提出了一种融合BN(Batch Normalization)[20]的全卷积深度学习网络的细胞显微图像分割算法，构建了具有多隐层的、融合BN算法的增强型U-Net深度网络。收缩网络中通过不断的卷积和池化操作获取图像特征，扩张过程则通过上采样和卷积操作来获取图像特征，并合并与之映射的收缩层特征补全丢失的边界信息，提升预测边缘信息的准确性；同时，为缓解深度学习网络训练时网络中间层的数据分布发生改变的问题，融入BN算法来标准化处理输入层及每一隐层的输入数据，将处理后的数据输入到网络的下一层中；优化了模型参数，提高了网络训练的速度及收敛性能；调整权值获取细胞的自动分割模型，实现细胞图像的精细分割。

2 细胞图像全卷积深度学习网络建模

2.1 全卷积增强型U-Net网络结构建模

传统的U-Net网络由23个卷积层、10个网络层构成。深度神经网络中包含中间层数目越多，该网络提取的图像特征越丰富，分割精度就越高，但同时也会造成计算量加大，需要更大的存储空间。为此，本文构建了基于BN与全卷积深度学习网络实现细胞图像分割。

在构建网络过程中，通过对训练过程中信息的损失率(loss)及准确率(accuracy)变化，综合确定合适的网络层数。对含有8个、10个、12个、及14个网络层的网络结构分别进行训练，得到相应的loss及accuracy结果如图1所示。

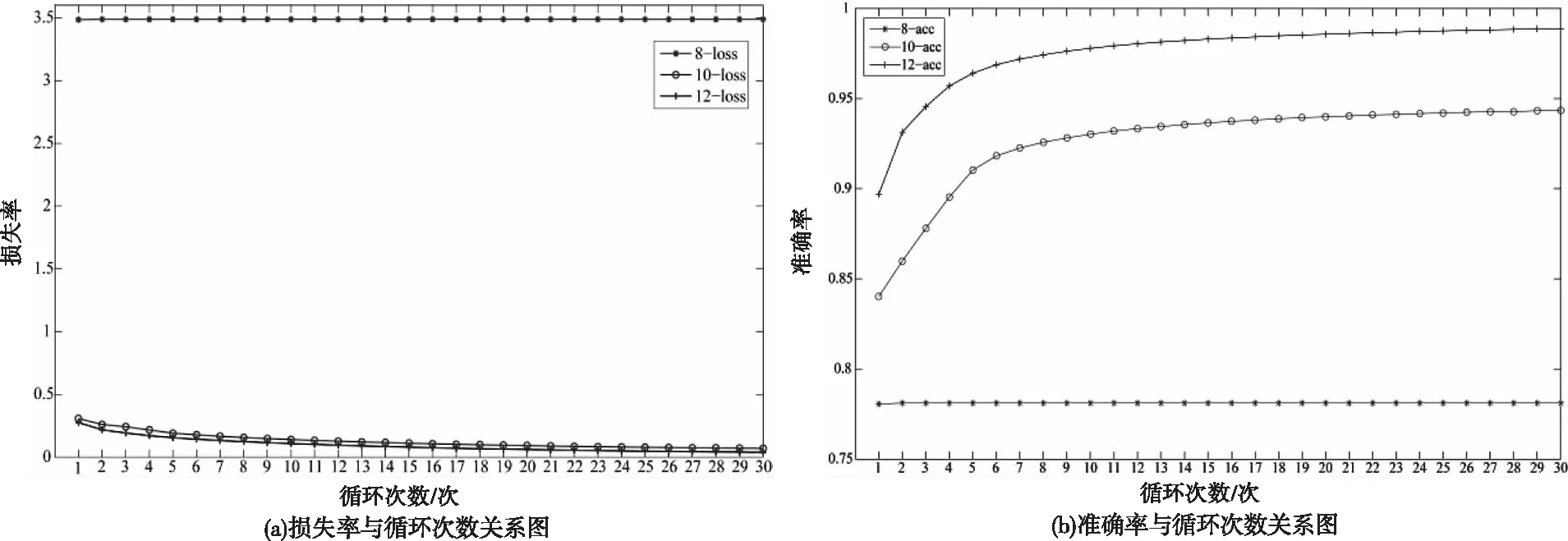
图1 不同网络结构训练中损失率、准确率与循环次数关系

由图1(a)、图1(b)可知，12层网络的loss较小，accuracy也明显高于10层网络，其收敛更好、更快；当继续增大网络层数时，网络计算量过大，超出计算机内存的支持，无法进行网络训练。基于此，本文构建了含有12个网络层的U-Net网络结构，即在原收缩网络中增加一个网络层，即增加2个3×3 卷积层和1个2×2 池化层，相应地，在原扩张网络增加一次上采样。

构建的全卷积网络中，收缩网络采用池化层逐渐缩减图像数据的空间维度，而扩张网络通过上采样层等网络层逐步恢复目标的细节和相应的空间维度；收缩网络与扩张网络间通过直接的信息连接，从而更好地恢复目标细节。该网络进行细胞图像分割流程如图2所示。

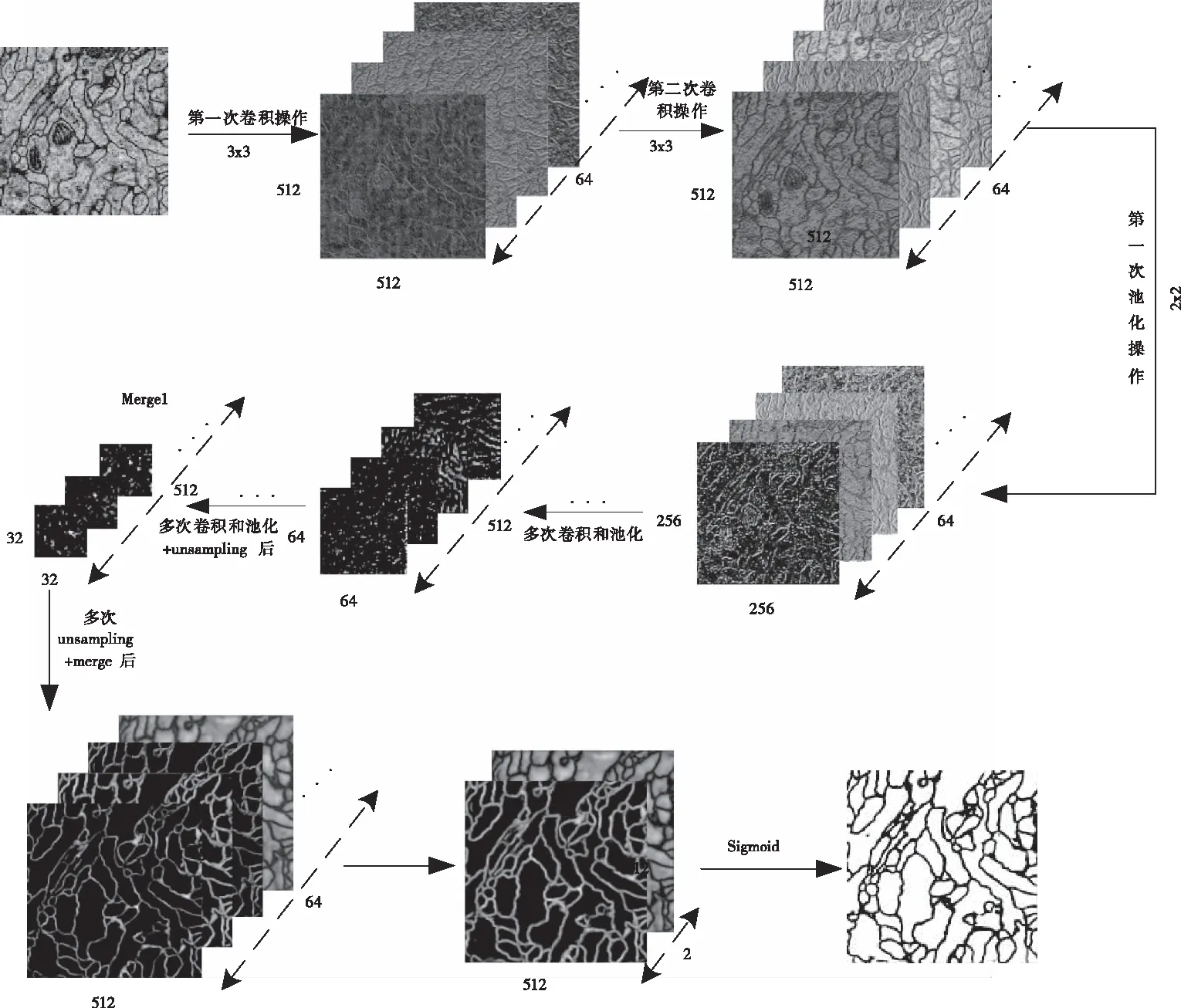
图2 全卷积深度学习网络图像分割流程

2.2 构建增强型U-Net网络的BN算法

网络训练数据与测试数据分布不同将导致网络的泛化能力降低，并且，若训练时每批次数据的分布各不相同，网络在每次迭代过程需学习适应不同的数据分布，从而降低了网络的训练速度；此外，网络训练时中间层输入数据的分布变化，层层累积致使网络高层的输入分布变化剧烈，以致于高层需要不断适应低层的参数更新，从而影响网络的训练速度。

U-net网络在网络数据输入中采用减均值、除标准差等方法[21]进行数据标准化处理，以降低样本间的差异性；该方法一定程度上降低网络输入端数据的差异性，但未解决网络中间层数据分布的变化。本文在网络中融入BN算法[20]，不仅可以标准化处理网络输入端的输入数据，还可标准化处理每一隐藏层的输入数据，将处理的数据输入到网络的下一层中。通过在网络中引入BN 算法独立地规范化每个输入数据，规范化的参数为最小批量尺寸数据的一阶和二阶统计量，实现了每个最小批量尺寸数据的统计量是整体统计量的近似估计，即近似同分布。

BN算法在每次迭代中归一化处理每层的输入数据，使得其数据分布为均值为0，方差为1。即[20]

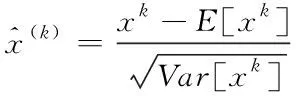
(1)

式中，xk表示第k维输入数据，E[xk] 为第k维数据的均值，Var[xk] 为xk的方差。

BN算法可将网络每层的数据分布固定，但缺点是强行归一化处理破坏了已学习的数据特征。因此，本文对原BN算法进行改进，解决以上不足。具体地：设置两个可学习变量γ 和β，利用其还原网络上一层已学到的数据分布，得到输出为[20]

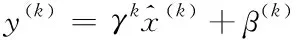
(2)

每个xk都有一对参数γ、β，训练中，正向传播不改变当前输出，得到γ、β；反向传播则根据γ和β通过链式求导，求出学习率来改变权值，恢复上一层数据所学到的特征；其中

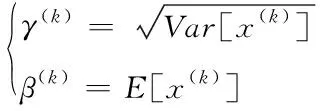
(3)

引入了可学习重构参数γ、β，使网络可学习恢复原始网络所要学习的特征分布；由此， 在全卷积深度学习网络中融合改进的BN算法可恢复网络上一层所学习的数据特征，具体地，在网络结构的卷积层后增加一个归一化层，做归一化处理后进入网络的下一层。

2.3 构建网络参数

2.3.1 构建缓解过拟合的网络循环次数

本文采用在网络中加入Dropout[22]操作及错误率最小的网络循环次数来缓解网络的过拟合。Dropout本质是在网络训练中以概率p 丢弃神经元，如图3(a)所示，因而，每次训练的网络仅为原网络的一个子网络，且子网络共享权重。即[22]

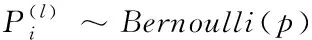
(4)

(5)

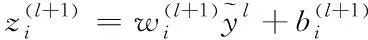
(6)

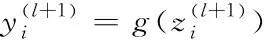
(7)

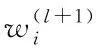
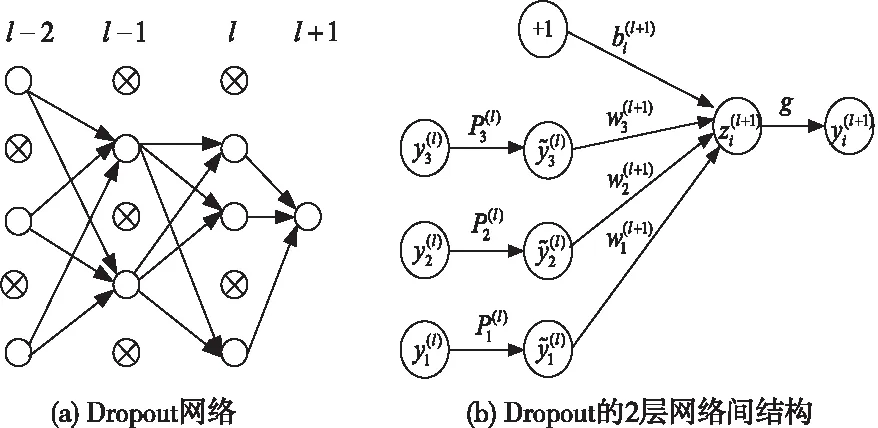
图3 Dropout网络模型(其中：⊗ 表示丢弃的神经元)

训练中，Dropout操作以概率p随机丢掉不同神经元改变训练的网络结构；由式(5)、式(6)知，其效果相当于对多个不同的网络训练结果取统计平均；不同网络结构训练中可能产生不同的过拟合，通过“统计平均”使过拟合得到有效地平滑，从而整体上减少了过拟合；其次， dropout操作的随机性使不同神经元未必每次都出现在同一dropout网络中，权值的更新不再依赖于有固定关系的隐含节点的共同作用，防止了某些特征仅在其它特定网络下才出现的情况，增加了网络鲁棒性。

训练中，当训练集的错误率继续减小，但验证集的错误率出现波动甚至增加，则此时网络的泛化能力开始变差，开始出现过拟合；此时，及时停止网络训练能够获得较好泛化能力的网络模型，以构建较为合适网络循环次数。如图4所示，其中，图4(b)为图4(a)中epoch为25-50的部分数据。从图中可知，循环次数37次后，随着循环次数增加，验证集的错误率开始出现波动，训练时间增大，综合考虑时间因素与错误率来确定较佳的循环次数。训练时，循环37次所用时间为42790s，accuracy为0.9855；循环30次的时间为33490s，accuracy为0.9845；两者相比，精度只相差0.001，但训练时间却明显缩短，最终，本文选取30次为网络训练的循环次数。

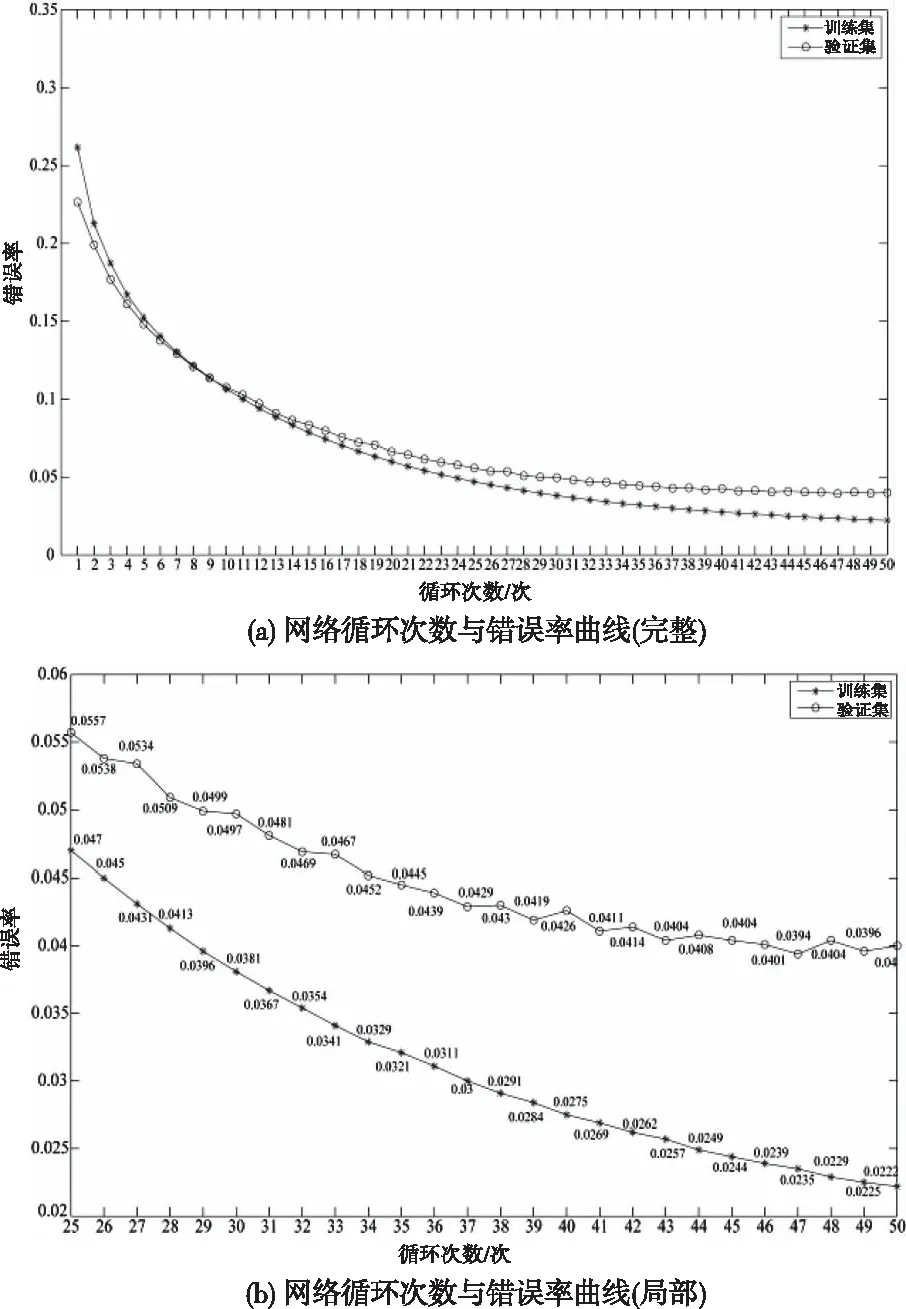
图4 网络循环次数与错误率曲线

2.3.2 设置批量尺寸

本文构建网络的误差反向传播使用批量处理方式，网络训练中批量尺寸(batchsize)设置决定了网络收敛的方向与收敛速度；批量尺寸为m的数据损失率(L)、梯度(∇ )分别为[20]

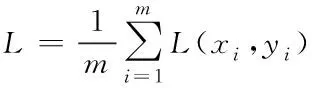
(8)

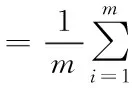
(9)

则其方差为[20，23]：

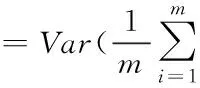
(10)

结合2.2节，数据满足独立同分布，因而有

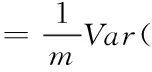
(11)

由式(11)知，批量尺寸为m时，数据方差减少m倍，从而提高了网络收敛速度。

GPU对2n的batchsize可发挥更佳的性能[23]，因此，本文选batchsize为2n测试；训练中，训练集大小为4900，循环次数为30次，在网络正常训练前提下，选取batchsize为1、2、4、8、…进行对比实验。结果如图5及表1所示。

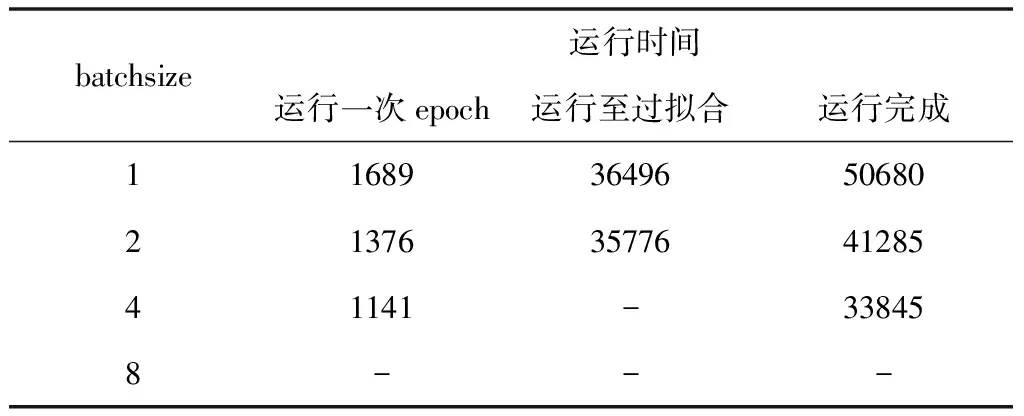
表1 不同batchsize运行时间对比(单位：s)

由图5及表1，batchsize=1，循环为22次时，损失率开始出现波动，产生过拟合，此时精度为0.9842，训练时间为36496s；batchsize=2，循环为26时， 损失率开始出现波动，产生过拟合，此时精度为0.9854，训练时间35776s；而batchsize=4无过拟合现象，训练完成后精度为0.9841，训练时间为33845s。batchsize为8时，计算机因内存不足无法训练；batchsize为1、2、4时精度相差不大，但batchsize=4的训练时间最短，且能使网络较平滑的收敛。综合以上因素，本文设置batchsize=4进行网络训练。

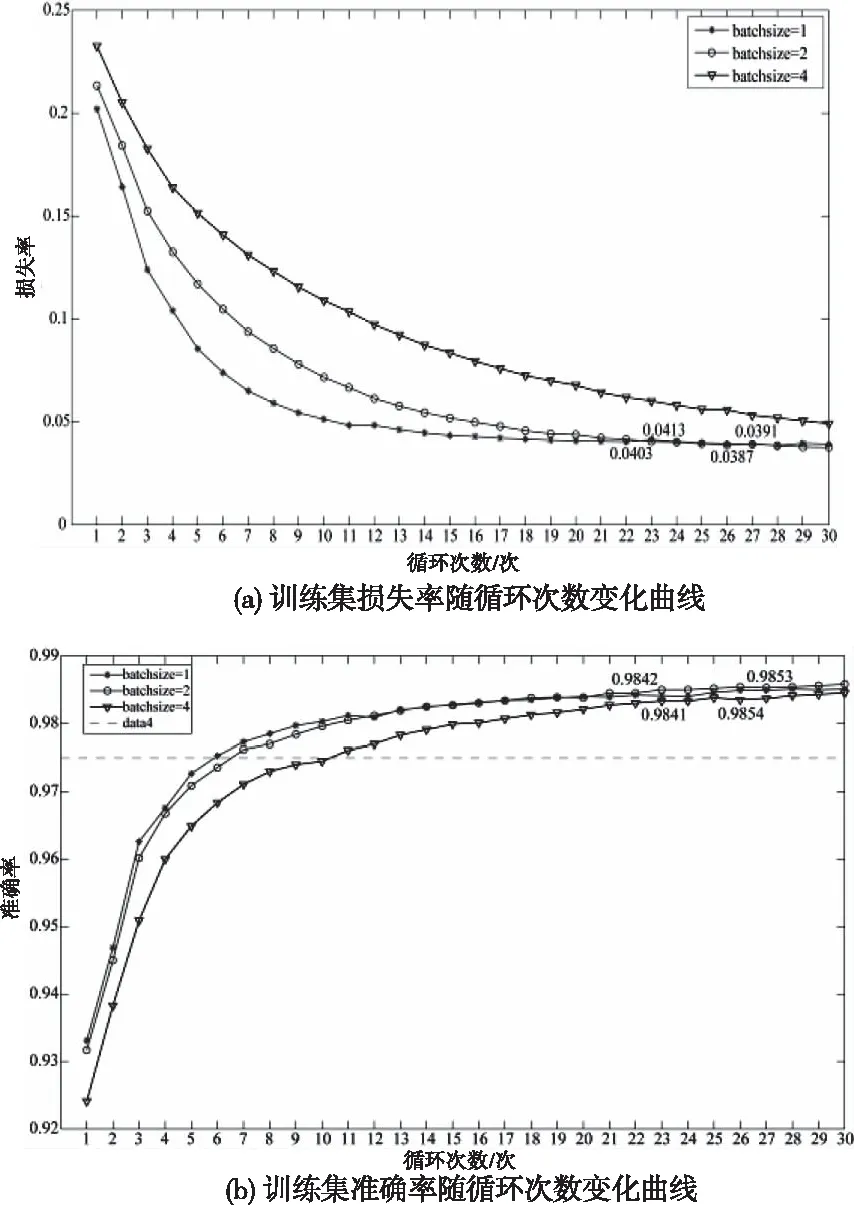
图5 不同批量尺寸下训练集损失率、准确率随循环次数变换曲线

2.3.3 确定学习率

学习率是优化算法中网络权重更新的幅度大小，影响网络的性能及其收敛性。自适应矩估计(adaptive moment estimation， Adam)[24]算法利用梯度的一阶矩估计和二阶矩估计动态调整参数的学习率，保证经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数θ比较平稳。调整过程[24]

mt=β1·mt-1+(1-β1)·∇

(12)

vt=β2·vt-1+(1-β2)·∇2

(13)

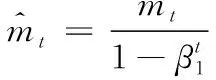
(14)

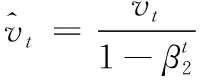
(15)

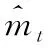
参数θ更新公式

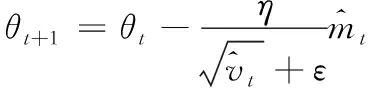
(16)

式中，η为学习率，常数ε设为10-8。

训练中，训练集为4900，迭代500次的条件下，结果如图7所示。由图6知，η=10-4时网络收敛效果最好，使网络能够较迅速且平滑的收敛，因此，本文选η=10-4进行网络训练。

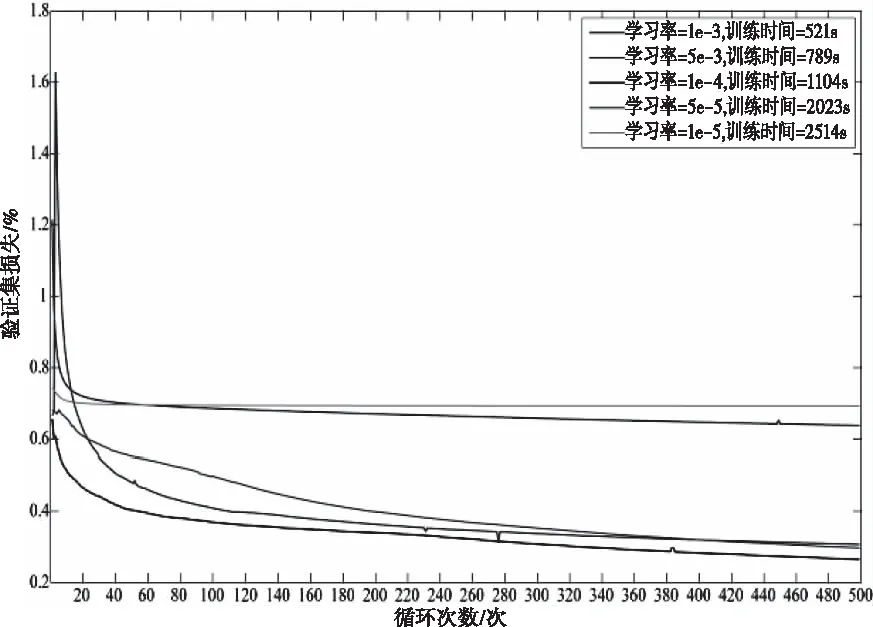
图6 不同学习率下验证集损失率随循环次数变换曲线

3 细胞图像分割的具体流程

应用第2部分构建的全卷积深度学习网络对细胞显微图像进行分割；分割算法分为训练与分割两部分；具体地：

1) 数据增强：实验采用ISBI2012竞赛组委会提供的公开数据集[25]；该数据集包含训练集和测试集两个图像库。为解决训练集过小问题，对原数据库的训练集数据扩增至4900幅图像；扩增时满足： ①增强所得数据与原始数据独立同分布或近似独立同分布，并采用相同比例对细胞图像进行扩增； ②增强后的数据集保留原图像的重要特征。扩增具体步骤：

① 基准图像作为训练集图像的一个通道，将训练集原始图与对应的基准图合并；

① 进行几何变换、随机弹性形变、随机缩放、逆时针剪切变换等数据增强操作；

① 图像增强后将合并图像分离，得到4900幅训练集图像和基准图像；

2) 数据预处理：将步骤1)中得到的训练集、基准图像进行0-1归一化处理，将数据转换为大小相同的矩阵输出；

4) 模型训练：采用对数损失函数binary＿crossentropy，使用Adam函数最小化损失函数，更新模型权重，并用验证集微调参数、优化模型；

5) 将细胞显微图像的测试数据集载入到训练好的网络模型中实现细胞显微图像分割。

4 实验结果及讨论

4.1 实验参数与评价指标

实验采用ISBI2012竞赛提供的公开数据集[25]，实验环境：AMAX台式服务器上采用Ubuntu14.04.1 LTS (GNU/Linux 3.16.0-33-generic x86＿64 )系统，显卡驱动：NVIDIA-Linux-x86＿64-367.44，TITAN X Pascal GPU1.531GHz；实验参数设置：旋转角度： rotation＿range=0.2，水平偏移：width＿shift＿range=0.05，垂直偏移：height＿shift＿range=0.05，缩放： zoom＿range=0.05，逆时针剪切变换：shear＿range=0.05，训练循环次数：nb＿epoch=22，学习率：η=1.0e-4， Dropout=0.5，训练集图像为4900幅。

采用概率Rand指数(probabilistic rand index， PRI)[27]、信息变化指数(variation of information， VoI)[28]、边界偏移误差指数(boundary displacement error， BDE)[29]和全局一致性误差指数(global consistency error， GCE)[30]作为客观评价指标。PRI描述算法分割与人工分割之间的一致性属性；VoI衡量算法分割与人工分割结果之间信息量的丢失情况；BDE反映算法分割结果与人工分割结果边缘像素间平均距离差；BDE∈[0，∞]，BDE值越小表示该算法分割结果的目标轮廓与人工分割结果差异越小，分割效果越好；GCE反映度量不同分割结果之间的一致性误差，GCE∈[0，1]，GCE值越小反映细化误差越小，分割效果越好。

4.2 实验结果对比分析

实验结果如图7、表2所示。

图7 五种不同算法分割细胞显微图像的效果比较(其中，纵向对应的四个测试图分别为图a、图b、图c、图d)

表2 不同算法分割结果的PRI、VoI、GCE、BDE评价指标比较

由图7知，从视觉效果上看， 相比于传统的Ostu分割、脉冲耦合神经网络(PCNN)分割、空洞卷积及U-Net分割算法，本文算法的细胞显微图像分割效果的清晰度更高，对目标区域的分割更精确；其原因在于，Otsu分割方法通过设置不同的阈值实现图像分割，分割时目标与背景差别越大，分割效果越好，但由于细胞图像的背景中存在大量噪声，影响了其分割效果；PCNN分割则是通过检测图像边界点，并多次迭代激活块区域，获取图像的目标区域信息，PCNN算法需要设置合适的门限参数；空洞卷积在增大感受野的同时卷积窗口不连续，并非所有的像素参与特征提取，损失了信息的连续性；相对于普通的U-Net网络分割，本文改进后的算法在原有的网络结构中增加了合适的网络层数，使得网络提取的特征更丰富，计算的精度更高，且构建的网络融合了改进的BN算法，加快了网络的收敛，改善了梯度弥散，从而，分割效果有了明显提高。

图8将原图a的五种不同分割算法结果左上角区域放大后，观察细胞分割结果的目标轮廓效果；由图可知，本文算法分割效果的轮廓信息最清晰，细胞边缘光滑性亦最好；U-Net算法次之，Otsu最差。

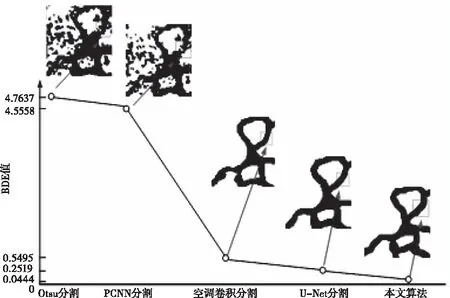
图8 五种分割算法边界偏移误差比较(图a结果)

由表2知，从客观评价指标看，本文算法的PRI提高0.04以上，高达0.99及以上，从而说明本文算法分割结果与人工分割图像属性一致性更高；本文算法的VoI为0.0879(图a)及以下，而U-Net算法为0.3382，空洞卷积算法为0.5500，PCNN与Otsu算法均在1.1以上，与信息量丢失较少的U-Net算法相比，本文算法信息量的丢失仅为其25.99%，反映了本文算法分割保留了较高的图像有效信息；本文算法的BDE相对于U-Net算法减少0.2以上，相对于空洞卷积算法减少0.5，相对于PCNN及Otsu则大幅减少4.5以上，说明了本文分割结果和人工分割图像结果边缘像素间平均距离更接近，即分割效果更接近与人工分割的效果；本文算法的GCE相对于U-Net算法减少0.04，相对于空洞卷积算法减少0.08，相对于PCNN及Otsu则大幅减少0.2以上，反映了本文算法分割结果的目标区域内一致性较好，U-Net算法次之，Otsu算法与PCNN算法的分割结果中出现大量离散点和孤立点。如图9所示。因此，本文算法的四个评价指标均优于其它几种分割算法，具有更好的分割精确和鲁棒性。

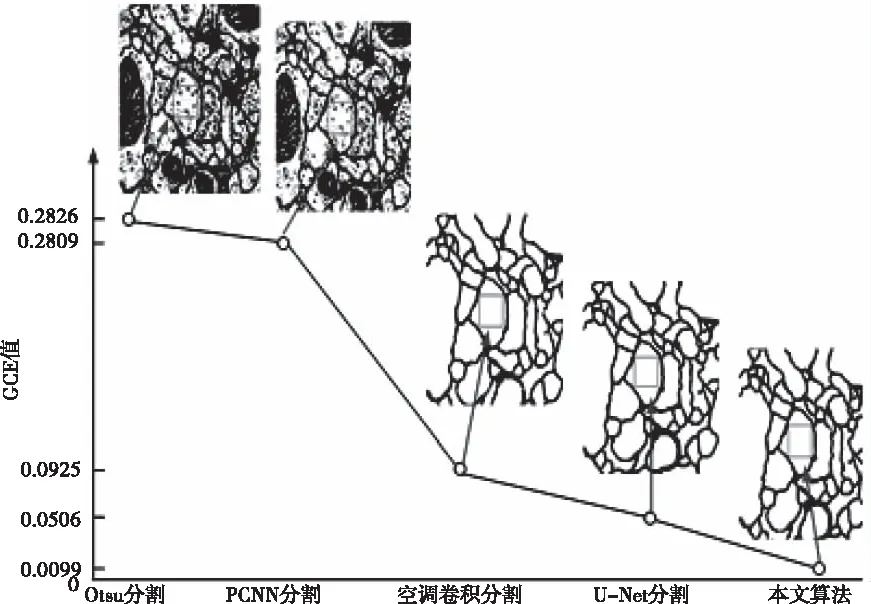
图9 五种分割算法区域内一致性比较(图a结果)

5 结论

本文提出了融合BN的全卷积深度学习网络的细胞显微图像分割算法；通过构建一个收缩网络和一个扩张网络组成的全卷积深度学习网络提取细胞图像特征，收缩过程通过卷积和池化操作提取图像特征，扩张过程通过上采样和卷积操作来获取图像特征，合并与之映射的收缩层特征补全丢失的边缘信息，提升预测边缘信息的准确性；同时，为缓解训练时网络中间层的数据分布发生改变致使高层输入剧烈变化而影响网络收敛的问题，构建改进的BN算法标准化处理输入层及每一隐层的输入数据，将处理后的数据输入到网络的下一层中；优化了模型参数，提高了网络训练的速度及收敛性能，实现了细胞显微图像的分割。

本文构建的深度学习网络结构应用于细胞图像分割时，输入图像大小非固定，解决了传统卷积神经网络(CNN)输入图像大小固定的限制，能实现端对端、像素到像素的训练。为保证本文算法的收敛性及泛化能力，在网络中增加了Dropout 操作，构建了错误率最小的网络循环次数，以此缓解过拟合现象。实验方案验证了本文方法应用于生物医学细胞图像目标检测和分割中的有效性与可靠性。