基于模糊权重的复合电源模型预测控制方法

杨朝红，马 彬，2，3，尹炳琪，陈 勇，2，3

(1. 北京信息科技大学机电工程学院，北京 100192；2. 北京电动车辆协同创新中心，北京 100192；3. 新能源汽车北京实验室，北京 100192)

1 引言

包含电池和电容器的复合电源系统，能够充分融合锂电池能量密度高、超级电容功率密度高的优点，可延长电池的使用寿命，最大限度的回收制动能量，被视为新能源汽车未来发展的重要动力来源[1，2]。车辆行驶过程中，道路坡度对车辆能量构建具有重要的影响，而精确的能量构建是影响功率分配效果的关键因素之一。因此，开发结合道路信息的复合电源能量管理策略，是目前研究的重要内容[3]。

目前，复合电源能量管理策略主要是基于规则、全局优化和实时优化三种主要控制策略[5]。其中，基于规则的控制策略易于实现，计算量较小，但主要依赖工程经验，无法保证最优的能量分配[4]；基于全局优化的控制策略以DP(动态规划)为代表，其不具有实时性，同时需要全局信息，限制了其大规模的工业应用[5]。而模型预测具有预测，滚动优化和反馈校正等优点[6]，因此在复合电源能量分配中广泛应用。Di Shen[7]提出了一种鲁棒模糊模型预测，并在能量管理控制器的设计中加入了交通状况；Chao Sun[8]提出了一种基于交通数据的能量预测管理框架；Fang Zhou[9]将滤波与模型预测相结合；Md. Abdus Samad Kamal[10]结合不同交通路况信息预测前一辆车的未来状态，并使用模型预测控制计算最佳车辆控制输入；Sina Moghadasi[11]利用遗传算法计算出优化后的成本函数权重矩阵；Oleg Gomozov[12]提出了基于非均匀采样时间概念的模型预测控制的实时管理策略；尹炳祺[13]提出了一种融合路况信息的车载复合电源模型预测控制方法；谢宪毅[14]利用模糊控制理论设计变权重系数调节器，实现最优控制参数的自适应调整；林泓涛[15]通过模糊控制对单一控制项权重系数进行优化，提升了控制效果。从当前的研究结果可以看出，道路信息已经在复合电源能量管理中获得应用，权重调节可以使控制策略依据实际工况自适应调整，但研究者们都没有依据坡度信息对权重因子进行调节，而坡度信息与权重调节对复合电源能量分配具有重要的影响。

因此，为了满足新能源汽车在实际道路坡度信息的需求功率，本文以复合电源系统为研究对象，提出了考虑道路坡度信息的基于模糊权重的复合电源模型预测控制算法。结合二阶Thevenin电池模型和RC电容模型搭建复合电源模型，在验证模型的基础上，建立了结合坡度信息的复合电源模型预测控制模型；以坡度、车速及相应的变化率为输入建立权重系数模糊调节器，对模型预测中的权重系数矩阵进行在线调整，提高了模型预测控制策略依据实际工况的自适应调整特性。

2 复合电源系统建模及验证

复合电源系统主要由锂离子电池、超级电容器、DC/DC转换器和控制器组成。考虑经济性和实用性，本文采用图1所示的复合电源半主动拓扑结构，其中锂离子电池组连接直流母线，超级电容器与 DC/DC转换器串联，经过功率变换后接到直流母线上。控制器通过测量锂离子电池和超级电容的荷电状态，经过计算后，对DC/DC转换器发出控制指令，主动调整DC/DC转换器的工作模式和超级电容器的充放电功率，从而完成复合电源系统合理的能量分配。

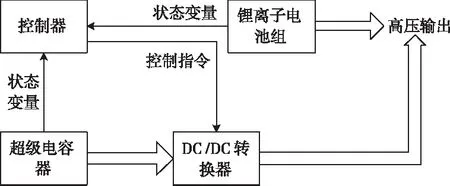
图1 复合电源结构

2.1 锂离子电池模型

目前常见的电池模型有电化学模型，神经网络模型，内阻模型，Thevenin模型和PNGV模型等。二阶RC等效电路具有精度较高且复杂性较低等特点[14]，因此本文选用二阶 Thevenin等效电路模型建立电池的状态空间方程。该模型由电压源、欧姆内阻和两个RC并联电路串联组成，电路形式如图2所示。

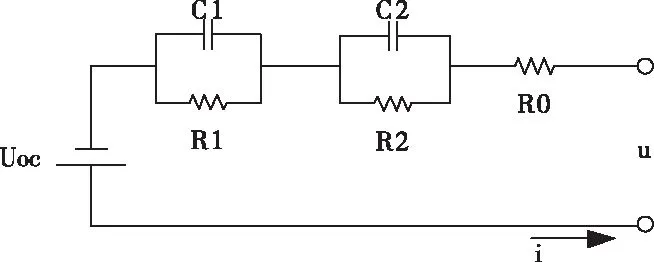
图2 锂离子电池二阶Thevenin等效电路模型

其中，u为电池的端电压；Uoc表示电池的开路电压，与电池SOC有关；R0表示电池的欧姆内阻；RC并联电路描述电池的极化特性；R1、R2表示极化电阻；C1、C2表示极化电压。

根据电池二阶Thevenin等效电路模型原理，电池的端电压计算公式为

u(t)=Uoc(t)-up1(t)-up2(t)-i(t)×R0(t)

(1)

式中，up1(t)和up2(t)分别为t时刻两个RC并联电路的端电压。Uoc表示开路电压，其大小与电池SOC相关，函数关系为Uoc=fUoc(SOC)。

采用Neware BTS4000电池测试设备、工作主机和Neware软件以及测试用锂电池进行充放电实验验证及参数识别，连接如图3所示。参数辨识结果如图4所示，验证结果如图5所示。

从图5中可知，在充放电循环工况下，电池端电压的仿真和实验结果可以较好的拟合，两者误差在0.07 V之内，满足精度要求。因此，二阶Thevenin等效电路模型可用于锂电池SOC的估算。

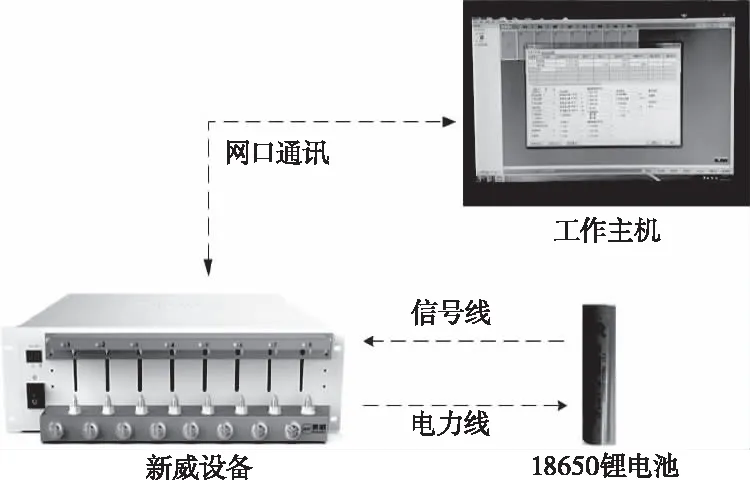
图3 连接图

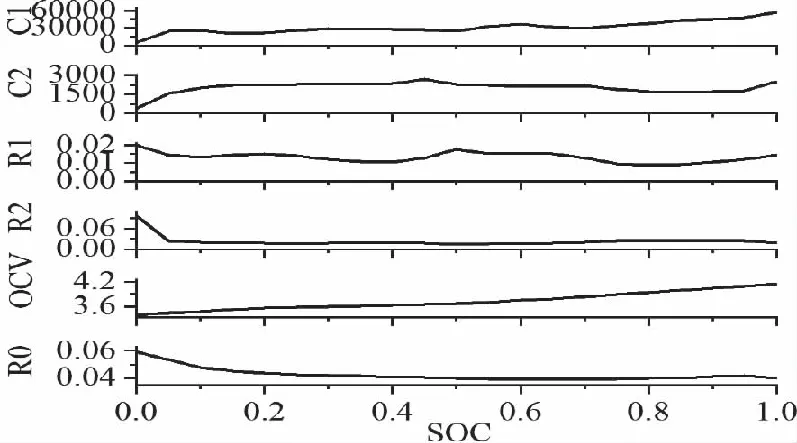
图4 参数辨识结果

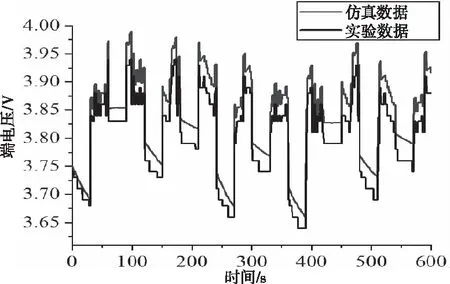
图5 电池端电压对比图

2.2 超级电容器模型

考虑到实际工程应用的需求和模型的精确度，选取典型的RC等效电路模型来表征超级电容器的充放电特征。所选取的RC等效电路模型如图6所示。

图6 超级电容模型

可以看出，该模型由一个电压源和电阻组成。其中，Ut为超级电容的端电压；Usc表示超级电容的开路电压；Rsc表示超级电容的欧姆内阻。

根据等效电路模型原理，超级电容端电压计算公式为

Ut(t)=Usc(t)-i(t)×Rsc(t)

(2)

为保证模型的精确性，采用16V Maxwell超级电容器进行充放电实验对模型的可靠性进行了验证，验证结果如图7所示。

图7 超级电容器端电压曲线

从图7中可以看出，超级电容端电压仿真曲线和实验曲线可以较好的拟合，两者误差最大为0.003V，满足精度满足。因此，所建立的RC电容模型可用于计算电容SOC。

2.3 复合电源状态空间

根据上述电池和超级电容器模型，构建复合电源状态空间模型。选取SOCBat和SOCSCs作为复合电源的状态量和输出量，选取电池功率PBat作为控制量。得到的复合电源状态方程为

Y=CX

(3)

其中

U=[PBat]，W=[Pt]

(4)

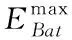
3 基于权重调节的模型预测控制方法

3.1 模型预测控制

模型预测控制的基本原理就是利用已有的模型、系统当前的状态和未来的状态量去预测系统未来的输出，通过滚动地求解带约束优化问题来实现控制目的，具有预测模型、滚动优化和反馈校正三个特点[16]。

线性模型离散化之后系统状态方程和输出方程为

Y(k)=CX(k)

(5)

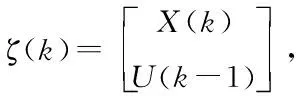
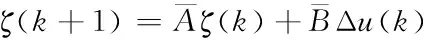
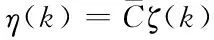
(6)

其中

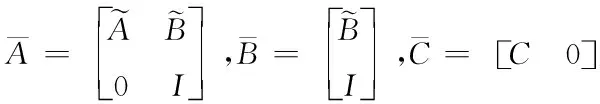
Δu=U(k)-U(k-1)

(7)

在预测时域为Np，控制时域为Nc的条件下，预测输出方程为

Y=Ψζ(k)+θΔU

(8)

式中

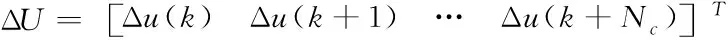
(9)

为了求得最优的电池功率，代价函数应取得最小值，其关系式如下

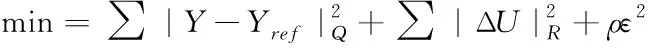
(10)

约束条件为

ΔUmin≤ΔU≤ΔUmax

Umin≤U≤Umax

Ymin≤Y≤Ymax

(11)

式中

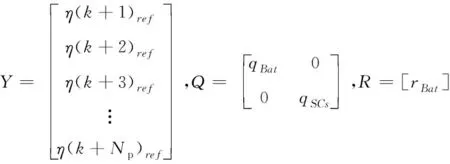
(12)

其中，Q和R为模型预测控制器的权重矩阵，qBat，qSCs，rBat分别代表了对电池SOCBat、电容SOCSCs和电池功率PBat的重视程度。

3.2 模糊调节器设计

当汽车以不同的车速行驶在不同坡度的路面上，为保证满足需求功率的同时避免电池大电流的充放电，需要对模型预测中关于电池SOC的权重因子建立模糊调节器进行实时调整。

建立模糊调节器控制规则，按照不同的车速和坡度及其相应的变化率对权重系数Kbat进行动态调整，针对模糊权重系数的复合电源模型预测的计算流程如图8所示。

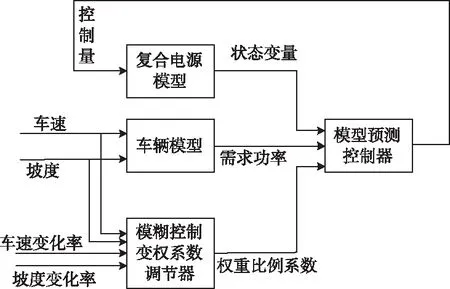
图8 变权重复合电源模型预测算法图

由图8可知，将车速、路面的坡度及其相应的变化率作为模糊控制器的输入，输出为权重系数Kbat，系统的输入输出模糊集分别为

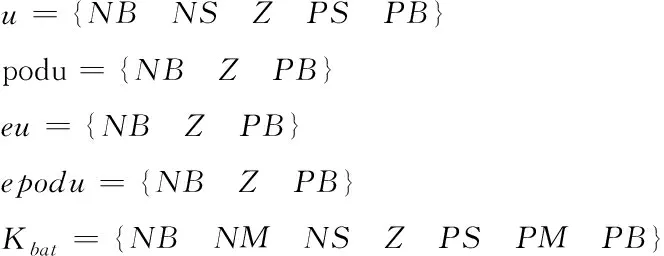
(13)

其中，NB为负大，NM为负中，NS为负小，Z为零，PS为正小，PM为正中，PB为正大，隶属度函数的取值为：u取值为[0，92]，podu取值为[-4，5]，eu取值为[0，92]，epodu值为[0，7.5]，其模糊规则如图9所示。

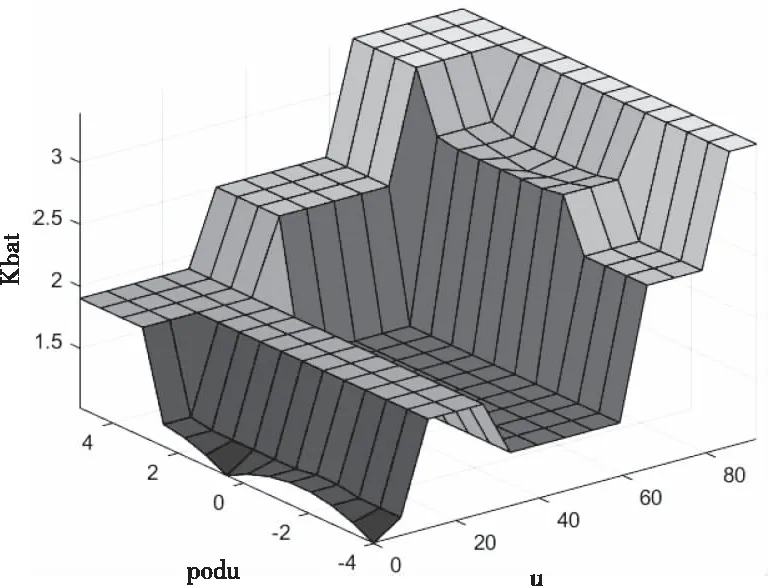
图9 模糊规则3D图

由图9可知，在速度为50km/h时，如果此时为下坡工况，通过模糊调节器能够输出调节系数为Kbat=1.3，此时抑制电池的充电电流从而使超级电容回收更多的能量，达到优化控制效果的目的。

通过模糊调节器，基于坡度、车速及其对应的变化率对权重因子进行实时调整，提高复合电源模型预测算法的实效性。

4 控制方法仿真结果及分析

4.1 考虑坡度后的功率需求构建

为了验证模糊权重的模型预测估算精度，采用如图10所示的仿真工况对复合电源进行仿真分析，其中上图为UDDS工况，下图为采集的北京某地的坡度信息。模型仿真需要设置初始值，其初始值设定如下：

表1 初始值的设定

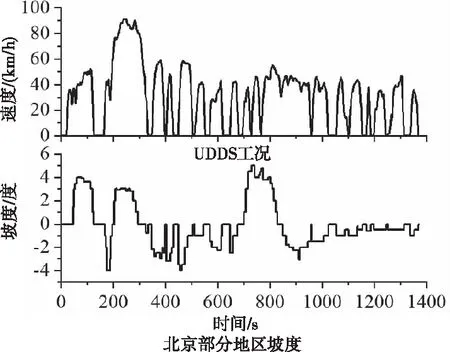
图10 UDDS速度工况和采集的北京某地坡度信息

图10中有两个典型阶段，在200-300秒的过程中，此阶段是加大速度爬坡工况，此时需要瞬间的大功率放电；在800-900秒的过程中，此阶段是下坡工况，需要电容器回收更多的制动能量。因此，在权重调节过程中重点考虑此类情况。

图11为有坡度和无坡度的车辆功率需求对比图，可以看出，在200-300秒的工况为加速上坡，此时考虑坡度信息后的功率需求显著高于未考虑坡度信息时的结果，在800-900秒时为下坡工况，此时需求功率比不考虑坡度时更小，所以，构建的能量需求更加符合实际工况。

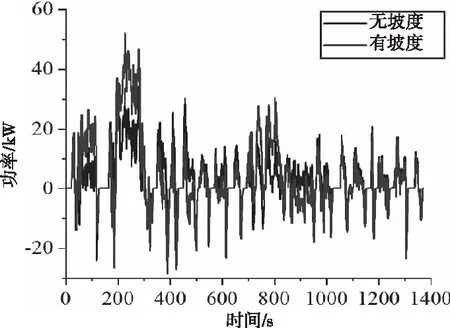
图11 考虑坡度后的功率需求对比图

4.2 功率分配结果分析

基于UDDS工况和实验采集的北京某地的坡度信息对复合电源模型进行仿真，复合电源电池、超级电容器功率、电流、电压仿真结果如图12-图15所示。

由结果可知，通过权重的模糊调节，能够显著提高复合电源的功率分配效果。从整个控制过程来看，所开发的控制策略能够依据坡度信息实时调整电池的基准功率，从而实现复合电源功率分配的优化调节。

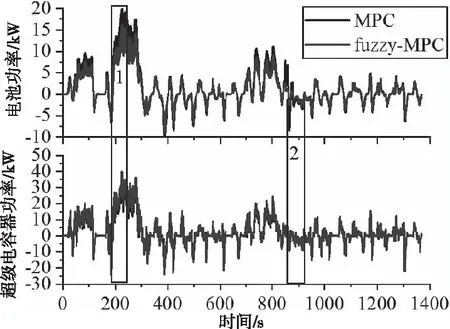
图12 考虑模糊权重后的功率分配对比结果

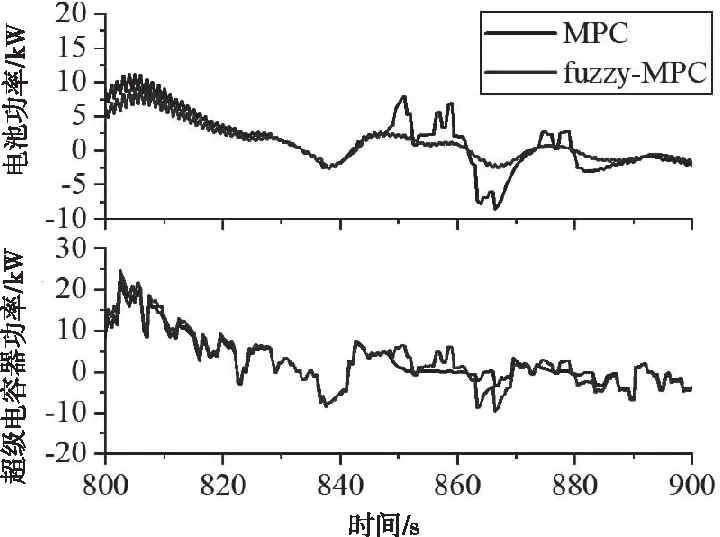
图13 考虑模糊权重后的功率分配对比结果：800-900秒的功率结果

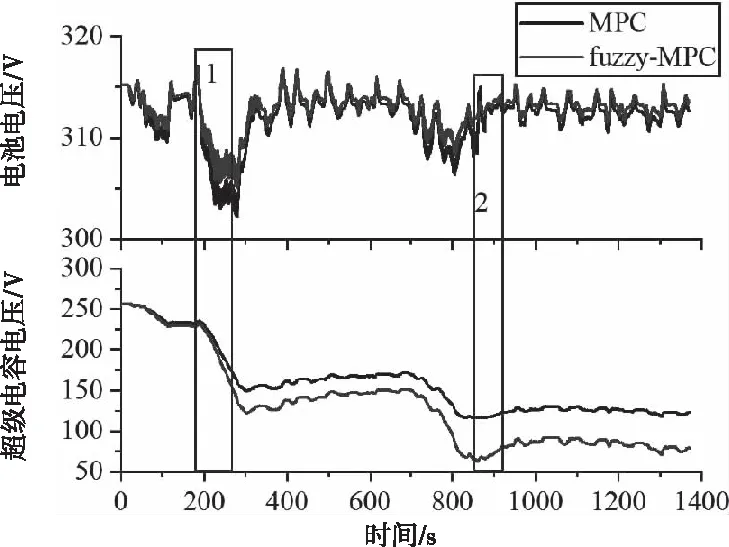
图14 考虑模糊权重后的复合电源系统电压对比结果

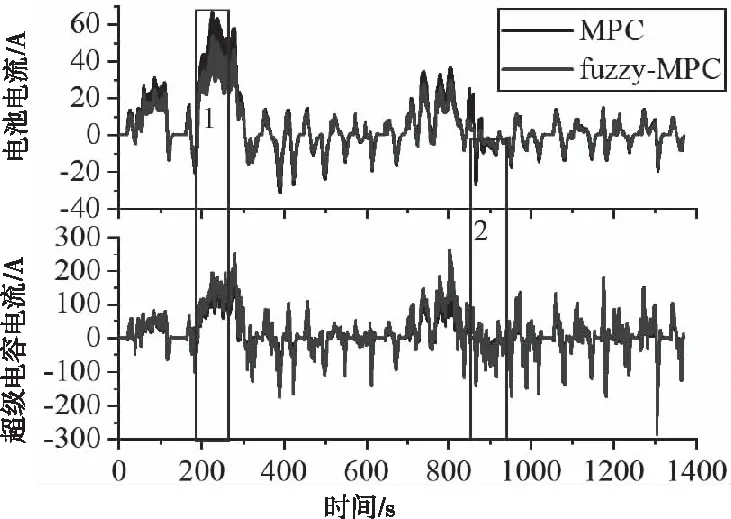
图15 考虑模糊权重后的复合电源系统电流对比结果

由图12的功率分配对比结果可知，在加速上坡阶段(阶段1)，考虑坡度信息后为保证下坡阶段电容器回收更多能量，此时通过模糊调节器增大电池权重，在满足超级电容器提供瞬间大功率的同时增加电容器的总放电量；由图15可知，此阶段限制了电池的放电电流，从而抑制电池放电功率，避免电池电压大幅度的下降，起到保护电池的效果，延长电池的使用寿命。在减速下坡阶段(阶段2)，由800-900秒的功率结果(图13)可知，考虑坡度信息后为保证上坡加速阶段电容器可释放更多的能量，此时通过模糊调节器减小电池权重，可使超级电容器充分回收制动能量；此阶段提升了超级电容器的充电电流和电压(图14-15所示)，从而增大超级电容器的充电功率，避免了电池大功率的波动。

为了更好的对两种控制策略的效果进行量化对比，将整个循环工况下超级电容器回收的能量整理如表2所示。由表2可知，基于fuzzy-MPC下的超级电容器回收制动总能量提升了9.1%。

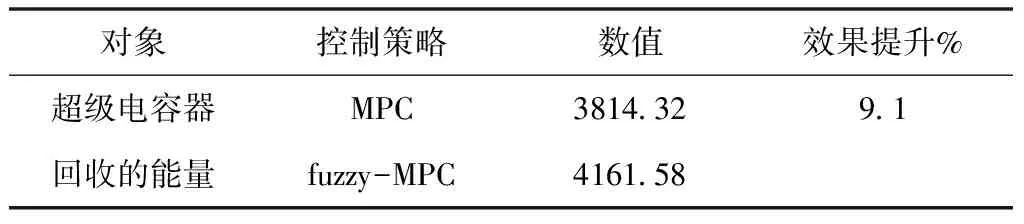
表2 两种控制策略的回收能量效果对比

4.3 控制过程SOC对比

基于UDDS工况和采集的北京某地的坡度信息在MATLAB/Simulink中对复合电源模型进行仿真，得到电池SOC和电容SOC仿真结果如图16所示。

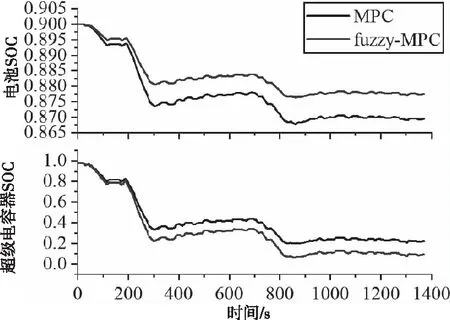
图16 考虑模糊权重后的复合电源系统SOC对比结果

从图16的仿真对比图中可以看出，在整个仿真工况中，模糊权重模型预测得到的电池SOC都比定权重模型预测得到的电池SOC更大，而fuzzy-MPC得到的电容SOC都比定权重模型预测得到的电容SOC更小。为了更好的量化效果，将200-300秒和800-900秒的复合电源SOC变化整理如表3所示。由表3可知，在上坡过程中，基于fuzzy-MPC下的电池SOC变化量减小了25%，电容SOC变化量提升了16.7%；同时在下坡过程中，电池SOC变化量减小了45%，电容SOC变化量提升了21.3%。

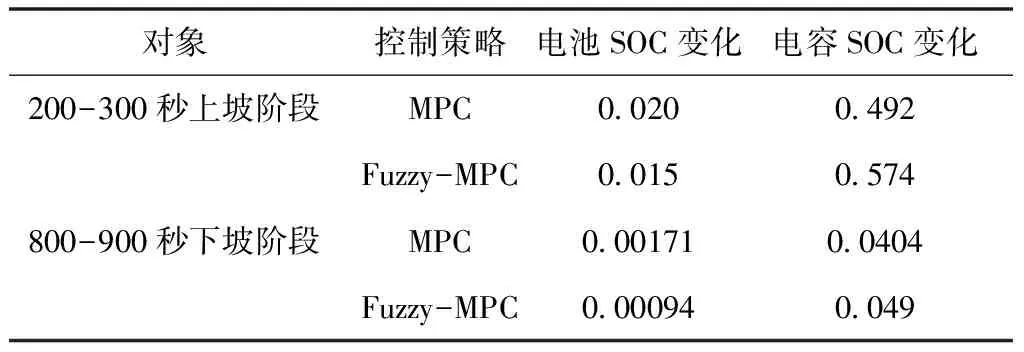
表3 两种控制策略的SOC效果对比

5 结论

本文提出了基于坡度信息和模糊变权重的复合电源模型预测控制方法。在建立、验证电池二阶Thevenin模型和超级电容RC模型的基础上，基于模型预测原理建立了考虑坡度信息的复合电源模型预测控制方法；基于模糊控制理论，以速度、速度变化率、坡度信息和坡度变化率为输入建立了权重系数的模糊调节器，对模型预测权重矩阵进行模糊调节，实现了模型预测控制依据实际工况的自适应调整；最后采用UDDS工况和北京市某地的坡度信息对复合电源模型进行仿真分析，结果表明，基于fuzzy-MPC下的超级电容器回收制动总能量提升了9.1%；同时在上坡过程中，电池SOC变化量减小了25%，电容SOC变化量提升了16.7%，在下坡过程中，电池SOC变化量减小了45%，电容SOC变化量提升了21.3%。研究成果为考虑坡度信息的复合电源功率分配、自适应、模型预测控制方法提供理论依据。