基于EMD的城市轨道交通混合储能容量配置
2022-05-14刘仕兵郭文璟宋陵灿
刘仕兵,郭文璟,刘 威,宋陵灿
(华东交通大学,江西 南昌 330000)
1 引言
地铁作为新兴的城市公共交通基础建设,具有运行密度高、周期长、站间距离短的特点,逐渐成为了广大市民出行的首选。近年来,城市轨道交通发展迅速,依据项目规划,未来全国地铁运营总里程将达到1.4万公里,遍及80个城市[1]。然而城市轨道交通能耗总量大、运维成本高,2015年北京市地铁运营有限公司年综合能耗 18.6万吨,二氧化碳排放总量达 81.7万吨,位居市重点能耗单位前列[2]。如何提升地铁各系统的运作效率、大幅降低系统运行能耗,实现“节能、低碳、绿色、环保”出行,是城市轨道交通节能减排工作的重中之重。可再生能源的应用是降低城市轨道交通系统能耗、提升系统能效的重要途径。分布式可再生能源接入轨道交通系统,既有助于实现分布式能源的就地消纳,减少弃风弃光,又有利于降低轨道交通的能源消耗,提升轨道交通供电系统的可靠性。
太阳能作为一种无污染,贮藏量巨大的环保能源,是当今人们可选择的最佳能源之一[3];风能作为一种分布广泛,使用方便的可再生能源,也早已应用到了人们的生产生活中[4]。利用风能和太阳能昼夜互补的差异性,达到联合供能的平衡状态,且大型风力、光伏发电厂的功率输出均已达到兆瓦级别,使新能源成为城市轨道交通的主要电力来源成为可能。但是光伏昼夜发电不平衡,风能在小的时间尺度上具有较大的随机性[5],为了缓解风能和光能的不稳定性对电网造成的影响,可利用混合储能系统(Hybrid Energy Storage System,HESS)储存可再生能源的电能,利用其平抑特性提升电能质量,减少轨道交通牵引网的建设投入。
近年来,有众多学者针对混合储能系统的容量配置做了相关研究。文献[6]利用小波分解研究了HESS的控制方法以及容量分配的问题,确定基波之后将信号分解成不同频带的分量,但分解出来的分量信号受基波选取的影响较大,导致重构出的信号会产生较大误差。文献[7-8]利用离散傅里叶变换结合运行成本分配混合储能系统功率,然而离散傅里叶变换计算过程复杂,对所处理信号精度要求高。经验模态分解(Empirical ModeDecomposition,EMD)在处理非线性波动信号时不需要事先选取基函数,且不会受到分解等级的影响,它能够将原始信号分解成数个具有不同物理意义的本征模函数(IMF)。文献[9]利用EMD算法确定不同储能装置的功率任务,结合费用效率评价混合储能系统的平抑能力。文献[10]在满足储能装置充放电特性的条件下,利用全寿命周期成本函数,计算储能系统重构分频阈值。孙威等人以微电网储能作为研究对象,计算超级电容及蓄电池的容量配置。利用蓄电池和超级电容器各自的储能特性,采用集合经验模态分解将微电网中电能信号分解成低频和高频分量[11]。
本文在前人研究的基础上,结合地铁运行时牵引负荷的功率需求特性,将由风力和光伏产生的电能储存到HESS中,利用HESS的平抑特性,实现风光互补。通过EMD算法将波动的电能信号分解成不同的频段,将高频段的信号输送到超级电容内储存,低频段的信号输送到蓄电池中储存,以减少储能成本及降低风光发电产生的电能波动对牵引网造成的冲击。
2 源-储-荷系统结构与建模
2.1 源-储-荷系统结构
图1及图2分别是白天和夜晚风光互补发电结合HESS为地铁系统供电的结构模型。Pw和Pv分别为风力和光伏发电的输出功率,Psc和Pba分别为超级电容及蓄电池的储能功率,Pload为地铁的牵引负荷功率。白天地铁运行时,风光发电系统将高频和低频的电能分别储存到HESS的不同储能装置中,HESS再通过DC/DC变换器将1500V电源输送到牵引网中。夜晚地铁不运行时,则仅由风力发电装置向HESS储存电能。

图1 白天风光互补发电及HESS向地铁系统供电结构图
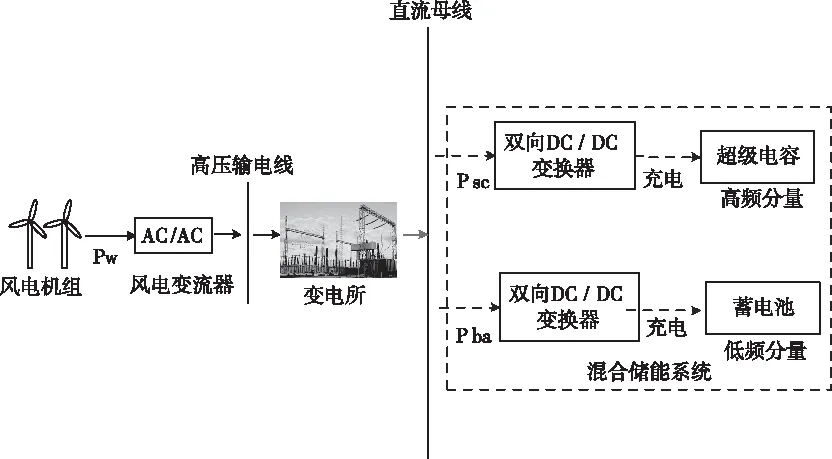
图2 夜晚风力发电向HESS储能结构
2.2 风光发电系统模型
2.2.1 风力发电系统模型
风力发电模型可分为两种:一种是考虑风机布置和风电场内部风速差的详细模型;另一种是采用同值等调法的单机等值模型[5]。本文可采取后者的方法将风电场等效为一个简化模型。
风机的发电功率与风速的关系可用下式表示[12]
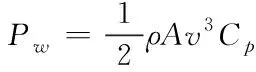
(1)
其中,Pw为风机输出功率,ρ为空气密度,A=πR2为风车叶片的扫掠面积,v为风速,Cp为风能利用系数。
风能利用系数Cp的值与叶尖速比λ有关,叶尖速比λ的计算公式如下[13]

(2)
其中,R为风车叶片的半径,ω为风轮的角速度,n为风轮的转速。
图3是某风力发电厂24h的风力发电功率曲线图。从图中可以看出风力发电在0MW~10MW之间波动,受风速影响,输出功率波动频率高,波动范围广,昼夜波动特性相似,主要在0点~7点及13点~17点波动剧烈。

图3 某风力发电厂24h发电功率曲线
风力发电功率的波动率计算式如下

(3)
式中,Fwind表示风电功率波动率,Pw(t)表示t时刻的风电功率输出值,Pw_N代表风电机组的额定输出功率,Pw_N=9.75,t为采样间隔,此处为5min。
由图4可以看出,一天中风力发电功率波动频繁,最高波动率可达到55.94%,远未达到国家并网要求,严重影响用电系统的电能稳定性。

图4 风力发电功率波动率曲线
2.2.2 光伏发电系统模型
影响光伏发电功率因素包括季节、天气、辐射强度、温度等,通常可用下式计算光伏输出功率[13]:

(4)

图5是某光伏发电厂24h的光伏发电功率曲线。由图中可以看出,由于昼夜太阳辐照度的差异,光能的产生主要集中在6点~20点,且在不同时段受到云层的影响呈现小范围的波动,其中,在12点~15点之间波动最为明显。

图5 某光伏发电厂24h发电功率曲线
光伏发电功率的波动率计算式如下
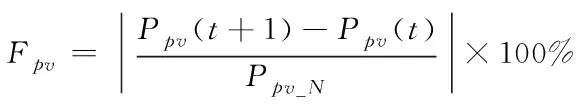
(5)
式中,Fpv表示光伏功率波动率,Ppv(t)表示t时刻的光伏功率输出值,Ppv_N代表光伏发电机组的额定输出功率,Ppv_N=0.95,t为采样间隔,此处为5min。

图6 光伏发电功率波动率曲线
由图6可以看出,光伏发电功率在日间也会出现较大的波动,最高波动率可达12.32%,同风力发电一样,也会对负荷侧的电能质量造成较大影响。
2.2.3 城市轨道交通牵引供电模型
城市轨道交通牵引供电模型如图7所示。风力和光伏发电厂产生的电能通过高压输电线输送到地铁供电系统的主变电所中降为35kV的交流电源,再通过牵引变电所中的整流器、变压器整合成为1500V的直流电源,供给牵引网,为列车运行提供电能。其中,混合储能系统中的超级电容和蓄电池分别串联DC/DC变换器,并联入直流母线中。混合储能系统的并入不仅可以储存电力机车牵引所需电能,而且可以削弱电能质量的波动对地铁运行造成的影响。
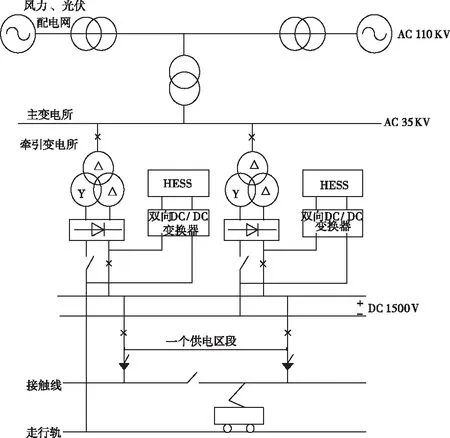
图7 城市轨道交通牵引供电模型图
3 储能容量配置
依据我国风力发电并网标准:风电机组装机容量低于30MW时,任意1分钟内有功功率变化范围不应超过3MW,任意10分钟内不应超过10MW[14]。我国光伏系统接入配电网技术规范GB/T29319规定电网频率需保持在49.5~50.2Hz,但为了保证更稳定的电能质量,入网的电网频率都保持在(50±0.1)Hz[15]。由于风力和光伏发电受到多种因素的影响,其稳定性远无法达到并网需求,故在能源与负荷之间接入混合储能装置用以平抑风、光发电的波动。
近年来,超级电容由于具有寿命长、功率密度大、响应速度快的优点,被广泛应用于微网系统的储能中[16],故可结合蓄电池组成混合储能系统。然而由于超级电容价格昂贵,蓄电池循环寿命短,在对混合储能系统进行容量配置时,若系统容量配置高于负荷需求则会增加投资成本,降低系统运行的经济性;若容量配置过低则会由于无法满足负荷需求而使储能装置频繁地切换工作状态,减少装置的使用寿命[17]。超级电容和锂电池的储能参数如表1所示。因此,为提高混合储能系统的经济性与稳定性,需对储能容量进行合理的分配。

表1 混合储能系统的配置参数
3.1 EMD原理
EMD作为一种自适应的非线性时变信号处理方法[18],其适用性已在分布式能源发电的功率预测、电力系统的故障分析等领域得到肯定[19]。通过将波动的非线性信号分解成一系列包含原信号不同时间尺度特征的本征模态函数(IMF)和代表原信号变化趋势的余项res来表征原始信号的不同特征[20]。
进行EMD处理前需满足以下条件:
1)信号至少具有一个极大值点,一个极小值点;
2)时间尺度特性由两个极值点之间的时间尺度确定。
EMD分解出的本征模态函数(IMF)需要满足以下两个条件:
1)所有数据范围内过零点的数据个数与局部极值点的个数必须相等或最多相差1;
2)任意时刻局部最大值的包络(上包络线)和局部最小值的包络(下包络线)的平均值需为零。
EMD算法的基本原理为:
a)确定原始信号X(t)的极大值点和极小值点,通过曲线插值的方法对这些极值点进行拟合,得到信号的上包络线Xmax(t)和下包络线Xmin(t);
b)对上下包络线求平均值

(6)
c)原始信号X(t)减去平均包络m1(t),得到余下信号h1(t)。对于平稳信号而言,即得到原始信号X(t)的第一个IMF。但对于非平稳信号,信号并不会在某一个区域内单调递增,而是会出现拐点。这些能反映原始信号X(t)具体特征的拐点若未被选中,则得到的h1(t)将会不准确,即通常得到的第一阶模态函数并不满足IMF的两个条件,故需进行进一步的筛选。
d)对余下信号h1(t)再次进行步骤a至步骤c的处理,直到SD(筛分门限值)小于门限值(一般取值0.2-0.3)时停止,从而获得所有满足条件的IMF,其中SD求法如下

(7)
e)对信号X(t)与满足条件的h1(t)求差,得到第一阶残差量r1(t),令r1(t)代替原始信号X(t)进行步骤a到e的处理,重复n次后即可获取第n阶模态函数hn(t)和最终符合标准的余量rn(t)。原始信号X(t)经EMD分解后的表达式为
(8)
故原始信号X(t)可用具有不同频率的hi(t)和余量rn(t)代表。上述过程可用流程图表示如图8所示。

图8 EMD分解信号过程
图9为风光互补输出功率经EMD分解后的IMF分量,IMF1~IMF5分别代表各阶的本征模态函数,res代表分解出的趋势性余项。

图9 经EMD分解后的IMF分量图
3.2 利用HT确定分频频率
经过EMD分解后的信号可以得到不同hi(t)值代表的IMF,我们可以通过找到一个合适的频率,不仅可以将不同频率的信号区分开来,而且尽量保证与区分频率值相邻的两个IMF频率混叠最少。
然而在傅里叶变换中,确定信号的瞬时频率至少需要一个完整的正弦波或余弦波[16]。对于频率随时间变化的非平稳波形,则无法满足上述条件。通过阅读文献[21],我们可以利用希尔伯特变换(HT)得到各个IMF分量的频率值,确定分频频率,进而将不同波动程度的信号区分开来。
将上述经EMD处理得到的分量h1(t)~h5(t)经过希尔伯特变换后得到的瞬时频率如图10所示。

图10 h1(t)~h5(t)的瞬时频率图
为了便于观察,去除掉频率波动剧烈,混叠范围较大的h1(t)及h2(t)的频率曲线,观察图11可得h5(t)的频率波动最为平缓,与其它分量的频率混叠最少,由实验数据可得,h4(t)在较大时间尺度范围内都在h5(t)的最大值8.4Hz以上波动,故选可择8.4Hz作为分配不同储能装置的分频频率。
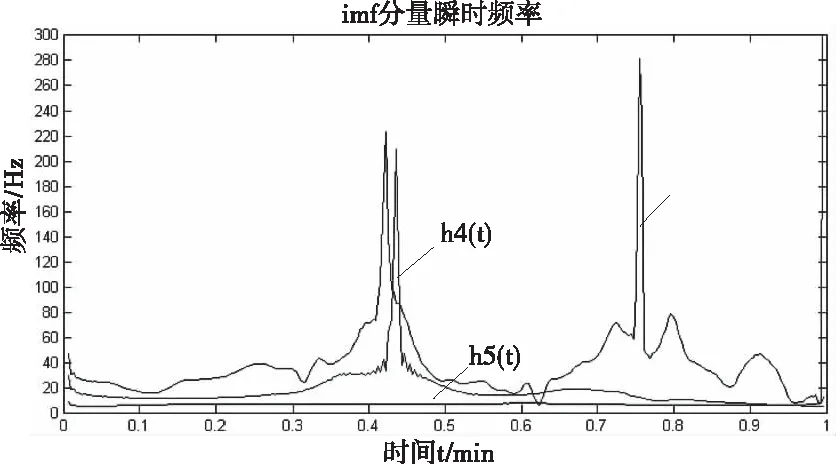
图11 h3(t)~h5(t)的瞬时频率图
3.3 HESS功率重构
在确定分频频率后,将包含不同频率的功率信号利用EMD重构算法重构出新的高频和低频信号。此时,信号的高频分量和低频分量可以表示为。

(9)
其中,k值越大,代表重构信号中所包含的高频分量就越多;k值越小,代表重构的低频分量就越多。重构出的高、低频分量如图12所示。
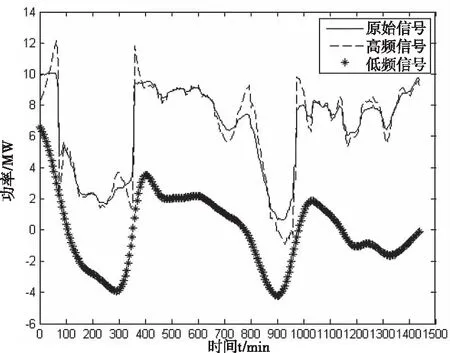
图12 高、低频分量功率信号
将频率较少变化但包含能量较多的低频信号分配给储能容量大的蓄电池储存,将频率频繁变化的高频信号分配给响应速度快的超级电容储存,从而达到能源的最优分配,改善地铁运行系统的稳定性与经济性。
4 结论
针对风光互补供电应用于城市轨道交通可能带来的电能波动问题,本文利用了混合储能系统,结合EMD算法计算出了混合储能系统的容量配置。通过算例分析,可得出如下结论:
1)利用EMD算法将不同特征的功率信号分离出来,摆脱了小波分解需要选定基函数的限制,可根据数据的时频特征进行分解,增强了数据处理的灵活性。
2)结合超级电容和蓄电池的储能特性,合理地配置了混合储能系统的容量,相较于风力和光伏直接供能,大大提高了电能质量,降低了地铁系统运行时电能的不稳定性。
3)本文仅利用希尔伯特变换得到的分频频率仍然不够准确,部分学者在提高分频频率的精度方面已做出相关探索,值得我们借鉴。文献[10]设置了滑动时窗来滚动计算储能目标功率,消除了分解过程的边缘效应。文献[17]采用离散傅里叶变换变换分解出次高频功率和次低频功率,提高了分解的精度。
4)风力、光伏发电接入城市轨道交通供电系统仍然有许多障碍需要克服,例如存在谐波、频率偏差、电压偏差等问题,需要我们做进一步的研究。
