高超声速气动热弹性分析降阶研究
2022-05-14晏筱璇韩景龙马瑞群
晏筱璇 韩景龙 马瑞群








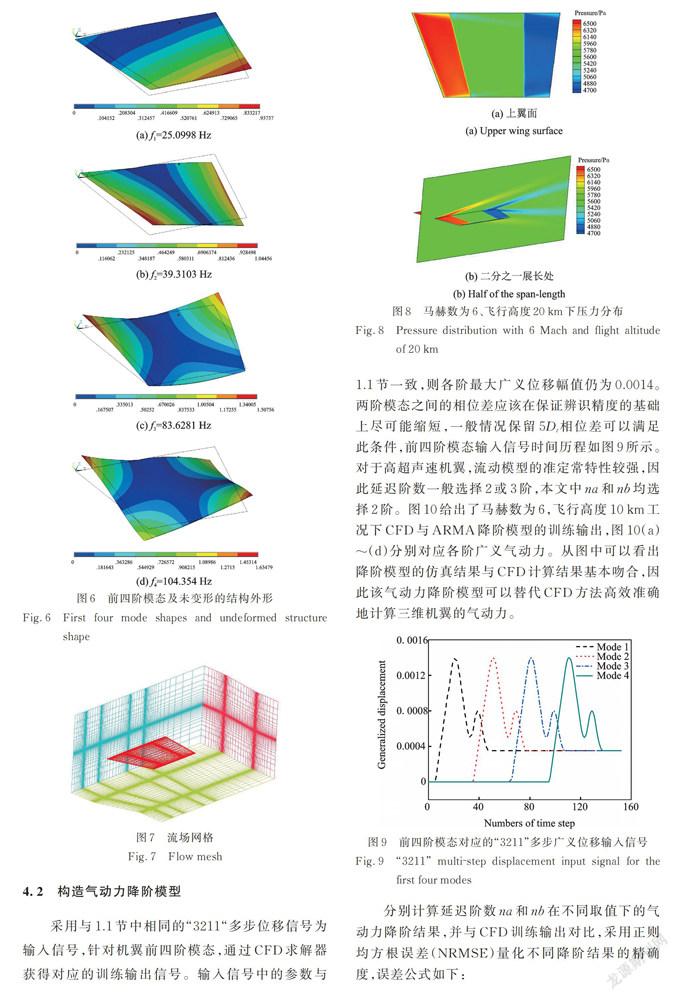
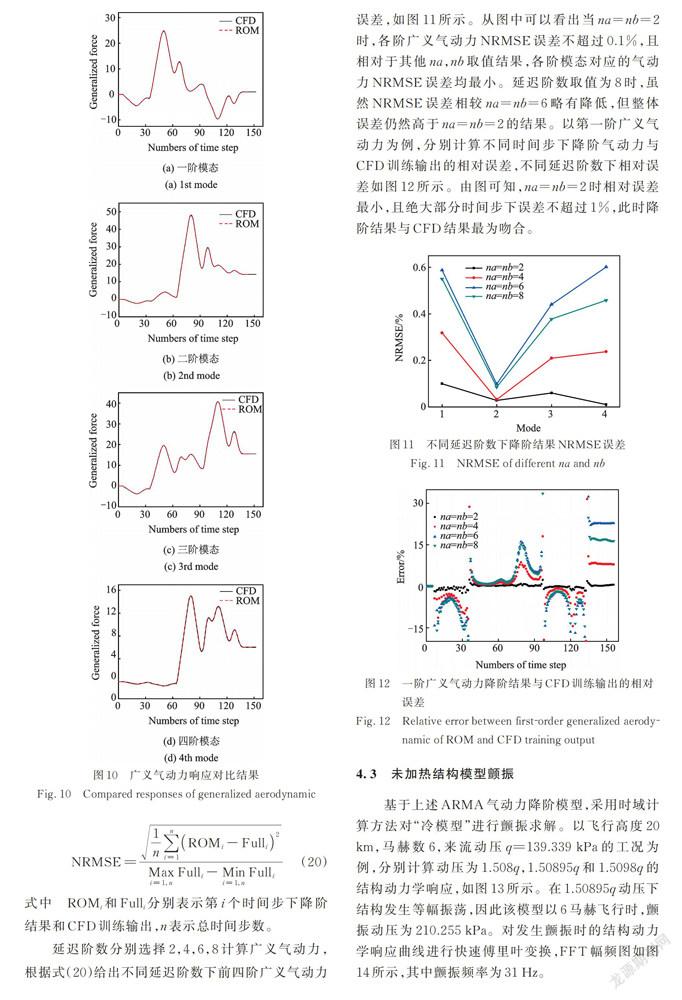


摘要: 高超声速气动热弹性分析涉及流场、结构场和热力场间的相互耦合,计算复杂且耗时长。根据分层求解策略提出了一种基于降阶模型的高超声速气动热弹性分析框架。分别采用系统辨识法和本征正交分解法对高超声速气动力和气动热建立降阶模型,并与模态叠加法耦合实现热配平状态下气动热弹性问题的快速计算。以典型高超声速三维机翼为例,预测热结构的颤振动压,并与全阶流⁃固⁃热耦合计算结果对比吻合较好。所提出的气动热弹性分析框架提高了計算效率,而且精度高,可应用于工程分析中。
关键词: 气动热弹性; 颤振; 高超声速; 耦合; 降阶模型
中图分类号: V215.3 文献标志码: A 文章编号: 1004-4523(2022)02-0475-12
DOI:10.16385/j.cnki.issn.1004-4523.2022.02.023
引 言
气动热弹性是一个复杂的涉及到多学科相互耦合的问题,依据现有的计算条件,采用高精度方法完全求解该问题是非常困难的。文献[1⁃2]在忽略气动热、气动力、弹性力与惯性力之间的弱耦合关系后,进一步简化该问题,提出了一种分层求解方法。该方法先计算定常气动热,认为非定常气动力不会对气动热产生影响,此外也忽略了结构变形对气动热的作用。本文基于分层求解方法进行气动热弹性建模,由于采用CFD求解气动热和气动力仍然耗时较长,故考虑了通过构造气动热和气动力降阶模型(ROM)来进一步缩短计算时间。
对于气动力降阶模型本文采用基于系统辨识技术的降阶方法。目前常用的非定常气动力辨识方法主要为Volterra模型、神经网络模型以及NARMAX( Nonlinear Auto Regressive Moving Average with Exogenous Input)模型。NARMAX模型是一种统一的非线性系统表达,例如Wiener模型和自回归移动平均(ARMA)模型等,该模型收敛速度快且精度高。ARMA模型可准确地辨识出弱非线性系统,常用于颤振稳定性问题中的非定常气动力辨识。Gupta等 提出一种基于状态空间方程的ARMA模型系统识别方法,可对飞行器的气动弹性现象进行精确而有效的模拟。张伟伟和叶正寅使用ARMA模型在辨识气动力方面开展了大量的研究,并分别将该模型应用于颤振计算,跨音速颤振的主动抑制研究以及阵风响应问题的研究[。Zaide等使用时域ARMA模型对随机阵风激发的CFD响应进行辨识,建立的降阶模型可以准确预测亚音速和跨音速下升力和俯仰力矩的时间历程。
本征正交分解(POD)是一种频谱方法,它通过正交基来近似全阶系统。该技术已被广泛用于描述流体力学中的物理现象。另外,近年来,POD技术也已经被用于高超声速气动热降阶研究。Falkiewicz等利用POD方法为时变热流通量边界条件下瞬态热传导问题构造降阶模型。Crowel等通过CFL3D程序获取高精度的结构表面热流密度,分别采用POD方法和Kriging代理模型对数据进行处理,建立气动热的降阶模型来估算表面热流。结果表明,基于Kriging的ROM比基于POD的ROM更准确,但POD方法的效率更高。Chen等分别采用了三种方法,即径向基函数(RBF)、POD⁃RBF和Kriging方法来构造ROM。Yan等提出了POD⁃Chebyshev气动热降阶模型,可用于预测高超声速飞行器的热平衡状态,计算效率和精度均高于Kriging方法。
本文运用ARMA模型对高超声速非定常气动力进行辨识,并与POD⁃Chebyshev气动热降阶模型结合,基于分层求解思路搭建气动热弹性分析框架。针对三维高超声速机翼,对其进行气动热弹性分析,并与CFD/CTSD计算结果比较,验证了本文提出的气动热弹性分析框架的可靠性。
