地震和列车制动力作用下铁路斜拉桥振动控制研究

2022-05-13郑成成郑久建陈永祁赵大海马良喆

铁道标准设计 2022年5期

郑成成,郑久建,陈永祁,赵大海,马良喆

(1.燕山大学建筑工程与力学学院,河北秦皇岛 066004； 2.北京奇太振控科技发展有限公司,北京 100037)

近年来，针对铁路桥梁在地震及列车制动力作用下的振动问题，学者们从不同角度进行了研究[1-4]。阎贵平等[5]通过分析典型铁路斜拉桥的地震响应，验证了输入地震激励的物理特性和车、桥动力特性是影响桥上列车运行稳定性、安全性及斜拉桥地震响应特性的主要因素；杨岳民等[6]通过对铁路桥梁车桥空间耦合动力响应问题的系统研究，提出了切合实际的桥、车耦合相互作用计算模型；王春贵等[7]提出了结构几何非线性效应在大跨度铁路斜拉桥车桥耦合振动分析中考虑的必要性；秦顺全等[8]在武汉天兴洲斜拉桥的减振设计中，首次提出了“磁流变(MR)阻尼器+黏滞阻尼器”的控制策略，用于控制行车荷载、列车制动和地震荷载引起的纵向振动响应；杨孟刚等[9]以某大跨度悬索桥为例，在地震和制动力作用下，开展了MR阻尼器在控制主梁较大纵向位移上的应用研究；颜志华等[10]首次将速度锁定装置应用在大跨度连续梁桥的减震设计中；吕龙等[11]研究了采用不同塔梁连接方式的公、铁两用斜拉桥在列车运行和制动作用下结构的动力响应，并详细分析了黏滞阻尼器设置在塔梁间时对主梁纵向振动的控制效果。

1 铁路桥梁的特殊性

铁路桥梁安全性和稳定性除通常考虑地震、强风和其他突发荷载外，列车正常行驶时产生的动力作用也是影响结构安全的因素之一[12]。尤其对纵飘桥梁而言，列车在通过桥梁时因加速、转向或制动等情况，给桥梁施加纵向振动荷载，使主梁产生较大的振动响应。与公路桥梁不同，铁路桥梁一般承担的货运或客运列车自身质量及承载质量都很大，其运行速度也很高。因此，当列车在桥上通过时产生的荷载比一般公路桥梁荷载大得多，尤其当列车在桥上制动时产生的刹车荷载属于较为复杂而剧烈的动力荷载，易引发桥体振动甚至舒适度问题[13]。

已有研究表明，设置在塔-梁间的黏滞阻尼器对桥塔和主梁纵向地震响应具有较好的控制效果，但由于列车制动力与地震荷载的大小和性能均差别较大，故阻尼器对列车制动力引起的主梁小速度纵向振动的控制效果相对有限[14]。因此，从分开控制的原则出发，研究协同工作组合控制体系对钢-混组合梁斜拉桥纵向振动响应的控制效果。

2 组合控制体系

2.1 带泄压阀的锁定装置

泄压阀锁定装置是内部经过特殊设计的一种减振器，泄压阀起到控制开关的作用。泄压阀的打开与关闭受装置所产生的力控制，其控制值对应于最大锁定力Fmax。在日常风荷载、行车荷载及列车制动力作用下，锁定装置出力一般在控制值以内，泄压阀关闭，锁定装置则发挥刚性连杆作用，牢牢锁住塔梁之间的变形。在控制主梁纵向振动位移的同时，将受到的力合理分配到附近桥墩，避免造成某一桥墩受力过大，从而改善了桥梁整体受力性能；一旦大风、强震等动荷载产生的力达到或超过最大锁定力，泄压阀打开，锁定装置立即退出工作。当强烈动荷载作用结束后，泄压阀自动关闭，可继续发挥常规锁定装置的作用。与对列车制动力同样有控制作用的MR阻尼器相比，泄压阀锁定装置性能更稳定(无需外接电路，不会因电路问题而出现无法工作的现象)。且该锁定装置在温度荷载等慢速作用下可自由运动，即在低速传递速度下允许结构自由变形。

泄压阀锁定装置可用下列公式进行模型化计算

(1)

式中，F为锁定装置两端实际受到的力；Fmax为最大锁定力；V为锁定装置两端所连结构的相对运动速度；V0为激发锁定装置工作速度。

目前，泄压阀锁定装置已成功应用在东平水道斜拉桥上，用于控制行车荷载等日常动力作用引起的振动响应。泄压阀锁定装置结构如图1所示。

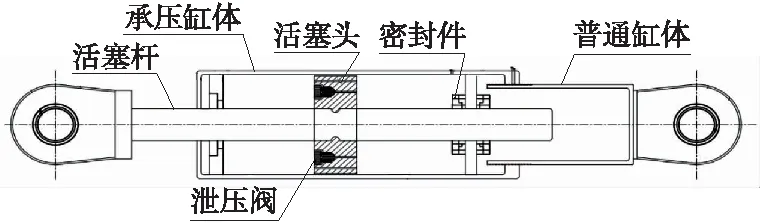
图1 泄压阀锁定装置

2.2 黏滞阻尼器

目前，桥梁减隔震领域普遍采用的黏滞阻尼器，主要由缸体、带射流孔的活塞、活塞杆、硅油和密封件等结构组成[15]。硅油作为阻尼介质，在活塞往复运动中起到黏滞作用，将地震产生的动能转化为热能耗散掉，从而对结构起到减震作用。此外，可通过改变射流孔的大小及形状来提供不同的阻尼系数和速度指数，以满足不同工程减震需求。由于温度荷载所产生的变形速度很小，阻尼器对温度变形及混凝土的收缩徐变不产生影响。图2为黏滞阻尼器结构。

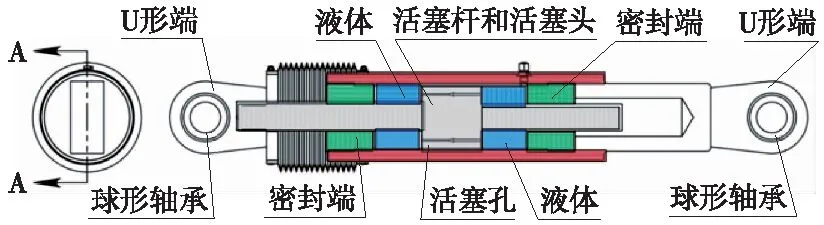
图2 黏滞阻尼器

黏滞阻尼器非线性计算模型为

F=CVα

(2)

式中，F为阻尼力；C为阻尼系数；V为阻尼器连接两端的相对速度；α为速度指数(取值0.2～2.0，常用取值一般为0.2～1.0)。

3 工程概况

某双塔双索面钢-混组合梁斜拉桥采用纵向无约束半飘浮体系，塔梁结合部及各辅助墩处均不设纵向约束。全桥共设8个桥墩，从左至右分别编号P1～P8，其中，P4～P5为主墩(塔)，P1～P3、P6～P8为辅助墩，跨径布置为(37+40+64+330+64+40+37)m，全桥布置如图3所示。

图3 全桥布置(单位：m)

中跨主梁采用单箱多室流线形扁平钢箱梁，边跨梁采用单箱多室混凝土箱梁，宽15.2 m，中心线处内轮廓梁高5.0 m。桥塔采用钻石形钢筋混凝土塔，空心矩形截面，主要由上塔柱、中塔柱、下塔柱及横梁组成。P4号、P5号桥塔塔高分别为146.0 m和131.5 m。上塔柱顺桥向宽7.0 m，横桥向宽17.9 m。塔间设上下两道横梁。上横梁高3.0 m，宽8.6 m；下横梁高6.0 m，宽10.1 m。全桥共有64对斜拉索，由镀锌钢丝组成，并采用钢箱锚将其锚固于上塔柱，扇形布置，标准间距8 m，边跨加密段间距3.5～4.0 m。塔上间距分别为2.4，2.6，2.8 m。

全桥基于Midas/Civil软件建立三维模型，如图4所示。主梁、主塔、桥墩均采用梁单元模拟，并考虑桥塔恒载轴力引起的几何刚度影响；斜拉索采用只受拉空间杆单元模拟，并利用Ernst公式修正弹性模量以考虑拉索的垂度效应；带泄压阀的锁定装置采用基于Kelvin模型的Lock-up连接单元模拟。

图4 铁路桥有限元模型

黏滞阻尼器采用基于Maxwell模型的Damper连接单元模拟。在地震响应分析中，认为桥梁变形已超出弹性范围，因此，只考虑黏滞阻尼器的非线性因素；体系阻尼采用Rayleigh模型，结构阻尼比取3%[16]。为方便计算，桥墩和索塔底部均采用固结形式。

4 动力特性分析

本桥采用多重Ritz向量法[17]进行动力特性计算，得到该桥前5阶自振频率、周期、振型参与质量及振型特点，如表1所示。

表1 斜拉桥自振特性

分析结果表明：该斜拉桥第1阶模态表现为周期较长的主梁纵飘耦合桥塔纵弯振型，符合半飘浮体系桥梁特点[18]。纵飘振型虽有利于减小结构的内力响应，但在地震和列车制动力作用下容易产生较大纵向位移；第2阶模态表现为主梁一阶对称横弯振型，第3、第4阶模态主要表现为主梁横弯耦合桥塔横弯振型；第5阶模态表现为主梁一阶对称竖弯振型。横向振型早于同阶竖向振型的现象反映出该桥横向刚度较弱。主梁横弯和竖弯振型都呈现出对称特点，主要因为全桥的质量、刚度及施加的约束大致以跨中为对称点均匀分布。

5 列车制动力与地震作用响应分析

5.1 阻尼器参数敏感性分析

速度指数α和阻尼系数C决定着黏滞阻尼器的性能，进而影响阻尼器对结构动力响应的控制效果。为确定合理的阻尼器参数，并保证黏滞阻尼器在地震作用下具有足够的安全储备，基于该工程安评报告中提供的3组峰值加速度均为0.3g罕遇地震波(50年2%)，对阻尼器进行参数敏感性分析，计算结果取其中一组最大响应值。考虑到对称及均匀分布原则，分别在南、北桥塔与主梁连接处各设置4个黏滞阻尼器，全桥共8个。速度指数α取值分别为0.2，0.3，0.5，0.7和1.0，阻尼系数C取值为0～5 000 kN·s/m，取值间距为500 kN·s/m。

利用非线性时程分析法分别计算无阻尼器和设置不同参数阻尼器的斜拉桥在罕遇地震作用下结构响应。桥梁结构各关键部位最大响应值随阻尼器参数的变化情况如图5～图8所示。

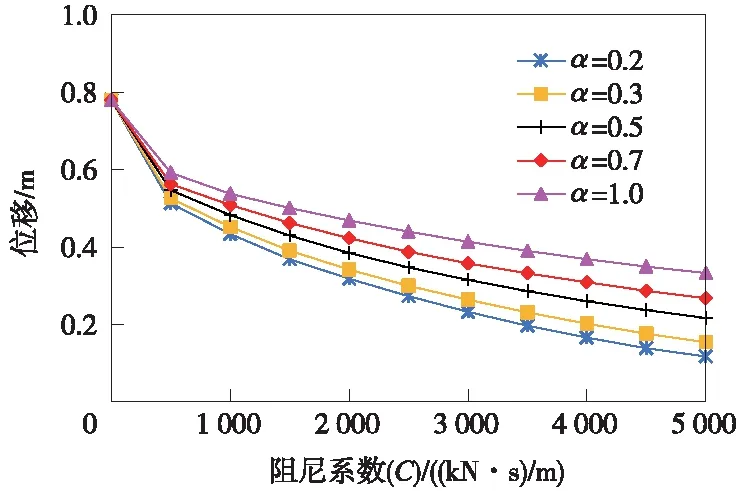
图5 梁端最大位移随阻尼器参数变化

图6 塔底最大剪力随阻尼器参数变化

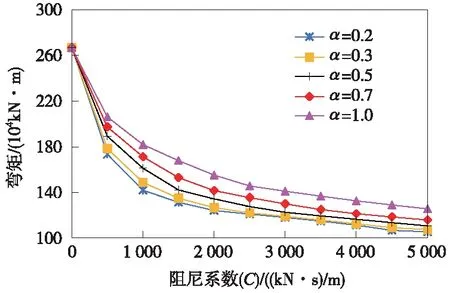
图7 塔底最大弯矩随阻尼器参数变化

图8 最大阻尼力随阻尼器参数变化

从图5可以看出，当阻尼系数C一定时，梁端最大位移随速度指数α的增大而增大；当速度指数α一定时，梁端最大位移随C的增大而减小，且当C增大到一定值时，位移衰减趋于平缓。对于该桥，当以主梁纵向位移为控制目标时，阻尼器参数倾向于α取小值、C取大值。当速度指数α取0.2～0.5，阻尼系数C取3 000 kN·s/m及以上时，位移衰减明显变缓，地震响应控制效果较好。

从图6可以看出，塔底最大剪力随阻尼系数C的增大而增大，随速度指数α的增大而减小。其原因在于阻尼器约束体系限制了主梁的纵向地震响应，从而产生了附加作用力使塔底剪力有所增大。

从图7可以看出，当C一定时，塔底最大弯矩随α的增大而增大；当α一定时，塔底最大弯矩随C的增大而减小。其变化趋势与梁端位移相近。

从图8可以看出，阻尼力随α的增大而减小，随C的增大而增大。而阻尼力的增大，一方面会造成阻尼器质量体积增加，提高阻尼器制作加工要求和施工安装难度；另一方面也提高了对塔-梁连接处的强度要求[19]。

综合考虑阻尼器参数变化对梁端纵向位移、塔底剪力与弯矩、阻尼力及经济性等控制指标的影响。确定最优的阻尼器参数为：C取4 000 kN·s/m，α取0.5。

5.2 列车制动力响应分析

列车在过桥时产生的制动力作为发生频率较高的日常荷载，容易引起半飘浮体系斜拉桥较大的纵向振动响应。为进一步比较带泄压阀锁定装置与黏滞阻尼器对列车制动力引起的主梁纵向振动响应控制效果，在每个塔梁连接处各设置2个锁定装置(黏滞阻尼器)，全桥共4个。主梁位移及速度响应结果分别如图9、图10所示。

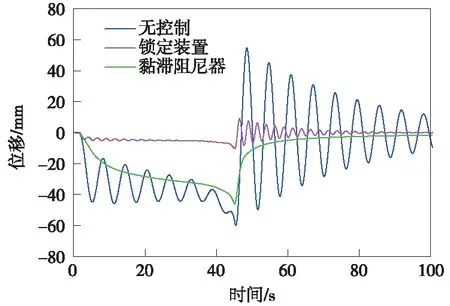
图9 主梁纵向位移控制效果对比

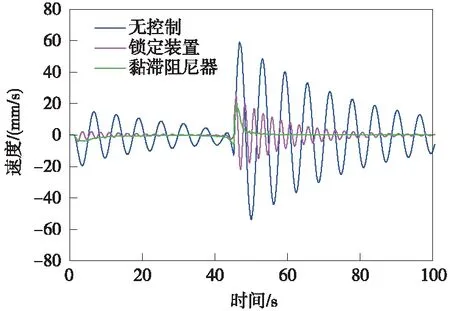
图10 主梁纵向速度控制效果对比

从图9可以看出，列车制动力作用下，无控制时主梁最大纵向振动位移为59.86 mm，设置泄压阀锁定装置后振动位移下降到10.17 mm，最大减振率为83.01%，满足美国AASHTO规范要求[20]；而设置黏滞阻尼器后振动位移下降到46.14 mm，最大减振率仅为22.92%。带泄压阀锁定装置对列车制动力作用下主梁纵向位移的控制效果优于黏滞阻尼器的原因在于：列车制动力引起主梁振动具有位移大而速度很小的特点，锁定装置对小速度振动相对更加敏感，而黏滞阻尼器因纵向振动速度太小而作用受限[8]。

从图10可以看出，列车制动力作用下，无控制时主梁最大纵向振动速度为58.25 mm/s，设置泄压阀锁定装置后振动速度下降至24.81 mm/s，最大减振率为57.41%；而设置黏滞阻尼器后振动速度下降至20.37 mm/s，最大减振率为65.03%。分析黏滞阻尼器对纵向速度的控制效果略好于泄压阀锁定装置的原因在于：黏滞阻尼器具有耗能能力，可通过阻尼力做功将一部分动能转化成热能耗散掉，使主梁因缺乏能量驱动而振动速度减小。

5.3 地震响应分析

限于篇幅，基于参数敏感性分析确定的阻尼器参数只进行罕遇地震下响应分析，结果取3组地震波中最大响应值并计算最大阻尼力。其结果如图11～图14所示。

图11 主梁位移时程对比

图12 塔底剪力时程对比

图13 塔底弯矩时程对比

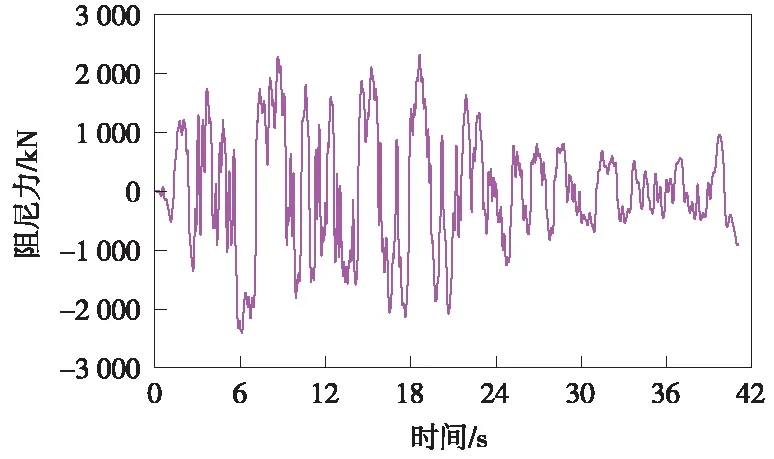
图14 阻尼器出力时程

从图11和图13中可以看出，在塔梁间设置黏滞阻尼器可有效控制斜拉桥纵向位移和塔底弯矩，其主梁最大纵向位移由控制前的0.78 m降至0.26 m，减震率达66.67%；塔底最大弯矩由控制前的2.667×106kN·m降至1.164×106kN·m，减震率达56.35%。从图12可以看出，由于阻尼器产生的抗力抑制了塔梁间相对位移，使塔底最大剪力略有增加，约10.87%，但远小于塔底抗剪强度。而黏滞阻尼器对主梁纵向位移和塔底弯矩的有效控制，在很大程度上改善了斜拉桥整体抗震性能。如此显著的减震效果，主要是因为黏滞阻尼器作为一种速度相关型的减震装置，对地震荷载引起的大位移、大速度结构响应很敏感，使其在地震发生时能很快进入工作状态并发挥作用。

从图14可以看出，在罕遇地震作用下，黏滞阻尼器最大出力为2 402 kN，远小于额定限值，始终在安全工作范围内。