FRP 加固 T 形截面混凝土连续梁弯矩重分布的数值模拟

田 新，施鹏飞，丁双双，缪宏兵，镇 斌

（1.南京方正建设工程质量检测有限公司，江苏 南京 210003；2.上海理工大学环境与建筑学院，上海 200093；3.如东恒一置业有限公司，江苏 如东 226400；4.如东锦恒城市投资集团有限公司，江苏 如东 226400）

0 引言

我国现有的服役建筑常受到结构改造或环境破坏等因素的影响，造成了现役结构承载力不足，因此需要纤维加固材料来提高结构的抗弯性能。采用纤维布加固两跨连续梁直接影响连续梁的弯矩重分布规律［1-7］。Kara 等［8-11］利用数值分析方法建立纤维布加固两跨矩形截面连续梁截面的受力分析模型，并模拟得到的截面弯矩-曲率关系，计算的截面抗弯承载力可研究连续梁跨中截面的实际抗弯性能。Oehlers 等［12-15］基于截面受力分析模型，得到的截面弯矩-曲率关系进行计算截面刚度，根据截面刚度情况获取各截面新刚度变化，最终得到各截面的模拟弯矩值，即可模拟实际工况下连续梁的弯矩重分布演变过程。但目前在 T 形截面两跨连续梁弯矩重分布理论还缺乏深入研究。本文采用数值分析方法对 T 形截面混凝土连续梁进行建模分析，并获取截面的新刚度进行连续梁的弯矩分配；采用刚度法模拟混凝土连续梁在不同加固区域的弯矩重分布系数情况，为现行服役的混凝土连续梁的加固设计提供技术依据。

1 工程概况

加固方案如表 1 所示，B-B1 至 B-C3 在支座处只粘贴 1 层纤维布，在跨中处底部粘贴 1～4 层的玄武岩纤维布和 1～3 层的碳纤维布以及 1 根未加固的对比梁，B-1～B-3 只在跨中底部粘贴 1～3 层的碳纤维布；同时在连续梁跨内加固处粘贴 U 型箍加强锚固，以避免 FRP 过早的脱落（见图 1）。

表1 试件加固方案

图1 连续梁加固设计示意图（单位：mm）

2 受力分析模型

2.1 基本截面假设

1）划分连续梁的各截面处的使用材料的变形情况满足基本截面假设。

2）假设加固连续梁的截面顶部到最底部的距离与截面几何高度基本相等。

3）纵向钢筋与混凝土表面粘结牢固。

4）不考虑混凝土连续梁发生剪切破坏及其他不利影响。

2.2 使用材料的应力-应变关系

分析截面尺寸、加固方式等因素后，模拟多跨连续梁各截面的应力-应变关系。受力分析模型中使用材料的应力-应变关系［16，17］如图 2 所示。

图2 分析模型中采用的本构关系

2.3 弯矩-曲率关系

分段连续梁，采用上述材料的应力-应变关系分析跨中及支座处截面受力情况。首先考虑划分条带，根据基本截面假设，得到i条带处混凝土的应变、跨中处受拉区混凝土形心处的应变、跨中处受拉区及受压区钢筋形心处的应变。

根据截面轴向力的平衡条件，得到：

式中：σci是受压区混凝土的截面等效应力，εci是截面混凝土第i条带处的应变，b为截面的宽度，x0为截面混凝土受压区的有效高度，As为纵向受拉钢筋的总面积，A′s为纵向受压钢筋的总面积，Af为纤维材料的总面积，σs为纵向受拉钢筋应力，σs′ 为纵向受压钢筋应力，σti是截面混凝土受拉区的应力，εti是截面混凝土受拉区形心处的应变。

根据截面矩的平衡条件：

采用计算机仿真，不断增加曲率K计算M值，得到弯矩曲率关系（M-K关系），程序步骤如下。

1）首先截面划分条带，并叠加曲率K值（K=K+ΔK）。

2）计算截面条带处的各使用材料的应变。

3）根据使用材料的应力-应变关系计算相应的应力。

4）再计算出截面轴向力是否符合条件。

5）若轴向力不满足平衡条件，重复步骤 3）～步骤 4）直至满足。

6）当超过使用材料极限条件时，程序结束。

依据文献［2］～［4］、［18］［19］提供的数据，利用上述原理，运用 MATLAB 软件编写伪代码拟合连续梁跨中底部粘贴 0～4 层 BFRP 布、1～3 层 CFRP 布及支座顶部相应的 1 层 FRP 布的截面弯矩-曲率曲线关系；对任一曲率，建立所构成材料相对应的截面应变，使用材料本构关系，计算相应材料的应力，再通过截面的轴向力平衡状态来获取所构成材料的弯矩值，并叠加得到截面弯矩M；不断重复迭代增加截面曲率，得到相对应的截面弯矩。最终通过混凝土极限压应变（εcu=0.003 8）和 FRP 极限拉应变来确定程序终止。

不完全规则的混凝土连续梁的截面尺寸在计算截面的应力-应变关系时，须考虑第一类 T 形截面与第二类 T 形截面，分析模型如图 3～图 6 所示。

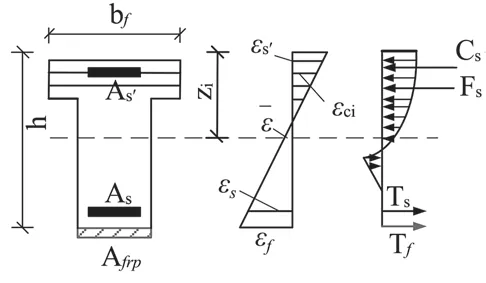
图3 第一类 T 形截面跨中处的截面受力模型

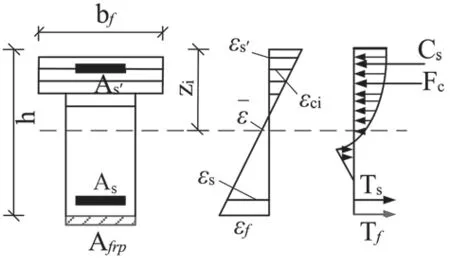
图4 第二类 T 形截面跨中处的截面受力模型

图5 第一类T形截面支座处的截面受力模型

图6 第二类T形截面支座处的截面受力模型

其中，εs是受拉区纵向钢筋应力；εs'是受压区纵向钢筋应力；εf是加固材料的应力；Fc是截面混凝土受压区压力；Cs是受压区纵向钢筋的压力；Ts是受拉区纵向钢筋的拉力；Tf是受拉区加固材料的拉力，bf是截面混凝土的翼缘宽度。

上述采用数值模拟得出的弯矩-曲率关系图呈三段变刚度曲线（见图 7～图 9），主要在开裂阶段、屈服阶段和极限荷载阶段这三个阶段。荷载刚开始加载时，截面会出现开裂，开裂弯矩并未随加固量的增加发生变化；继续施加荷载，此时截面出现刚度首突变情况，截面钢筋出现屈服现象，施加在截面处的弯矩会随加固材料的增加而变大；再继续施加荷载，截面刚度增长的幅度开始下降，但截面处的弯矩仍增大，并随着加固材料的增加而变大。

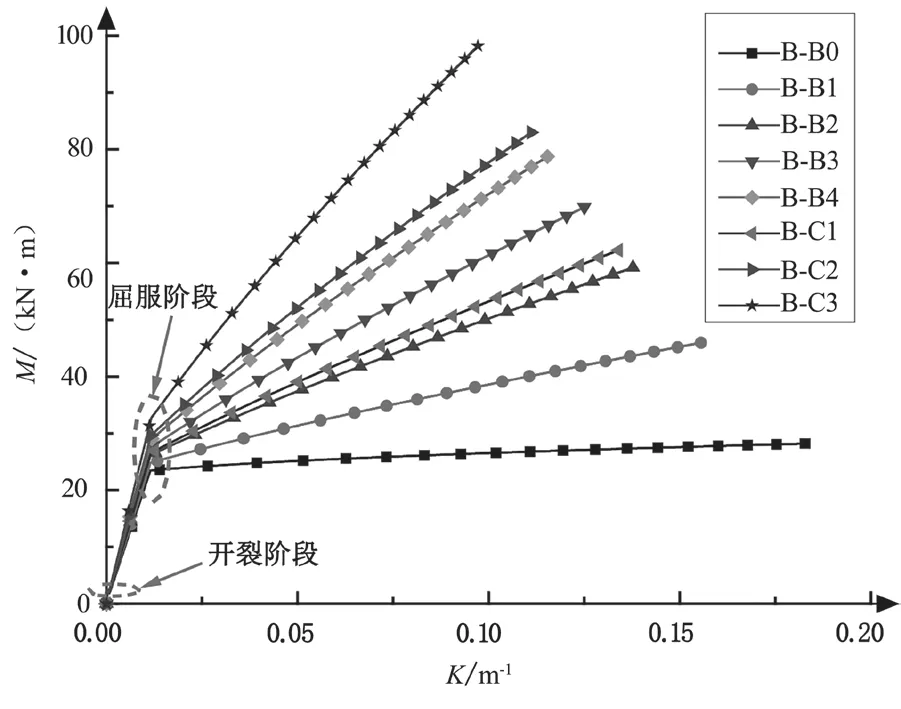
图7 跨中处 B-B0 至 B-C 3 构件数值分析的弯矩-曲率关系

图8 支座处 B-B0 至 B-C1 构件的数值分析的弯矩-曲率关系

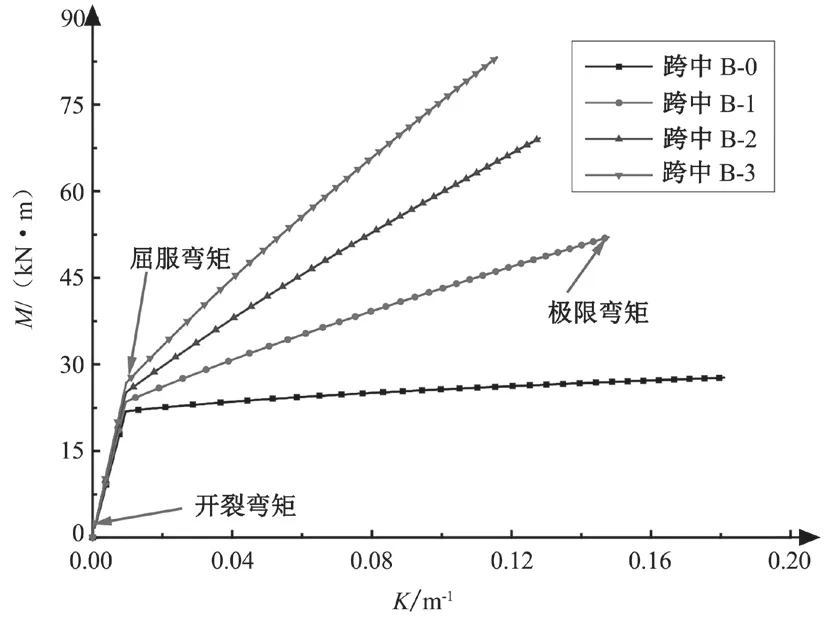
图9 跨中处数值分析的弯矩-曲率关系

3 弯曲刚度法

采用刚度法的假定主要考虑截面上的刚度EI（E是材料弹性模量，I是截面惯性矩）不断变化且在支座处存在斜率连续性。试验梁模型如图 10 所示。

图10 试验梁模型

采用上述理论模型，并获得各截面的弯矩－曲率的关系，从而可计算两跨连续梁的各截面刚度（EI=M/K），可获得支座处的截面刚度EI2和跨中处的截面刚度EI1，通过截面刚度变化分配迭代整个连续梁截面上的新弯矩。

式中：l是梁跨长，P是载荷，EI1、EI2分别是跨中和支座处的截面刚度，x是试验梁的弯矩拐点处，Msag为连续梁跨中处的模拟弯矩，Mhog为连续梁支座处的模拟弯矩，βsag为连续梁跨中处模拟的弯矩调幅系数，βhog为连续梁支座处模拟的弯矩调幅系数。

采用刚度法迭代步骤：

1）调用上述各截面上的弯矩－曲率，可计算支座和跨中处在三个阶段（见图 10）的刚度。

2）施加一个荷载值，代入公式（3）中的第一个等式。

3）根据已有的固定荷载和刚度值，迭代公式（3）中的第二个式子中的拐点位置x值，直至公式两边等式相等，程序即停止。

4）若公式（3）不满足条件，可重复步骤 2）及步骤3）直至满足，可算出支座处分配的新弯矩M。

5）代入公式（4）和公式（5），计算P作用下连续梁支座处的弯矩重分布系数β=1－Ma/Me，Me为理论弯矩值。

由表 2 分析，当支座的纵向钢筋屈服后，构件B-B1～B-C1 在支座处的弯矩调幅系数值最为显著，依次为 -29.2 %、-38.4 %、-21.2 %、-21.0 %、-36.4 %，对应的数值模拟弯矩调幅系数依次为 -25 %、-38 %、-23.6 %、-19 %、-39 %，模拟情况基本上与实际试验梁的弯矩调幅系数一致；构件 B-B1～B-C1 在跨中处的弯矩调幅系数依次为 17.6 %、23 %、13 %、12.3 %、22 %，对应的数值模拟弯矩调幅系数依次为 16.4 %、23.2 %、15 %、12 %、24 %，模拟结果与实际试验梁的弯矩调幅系数基本吻合。

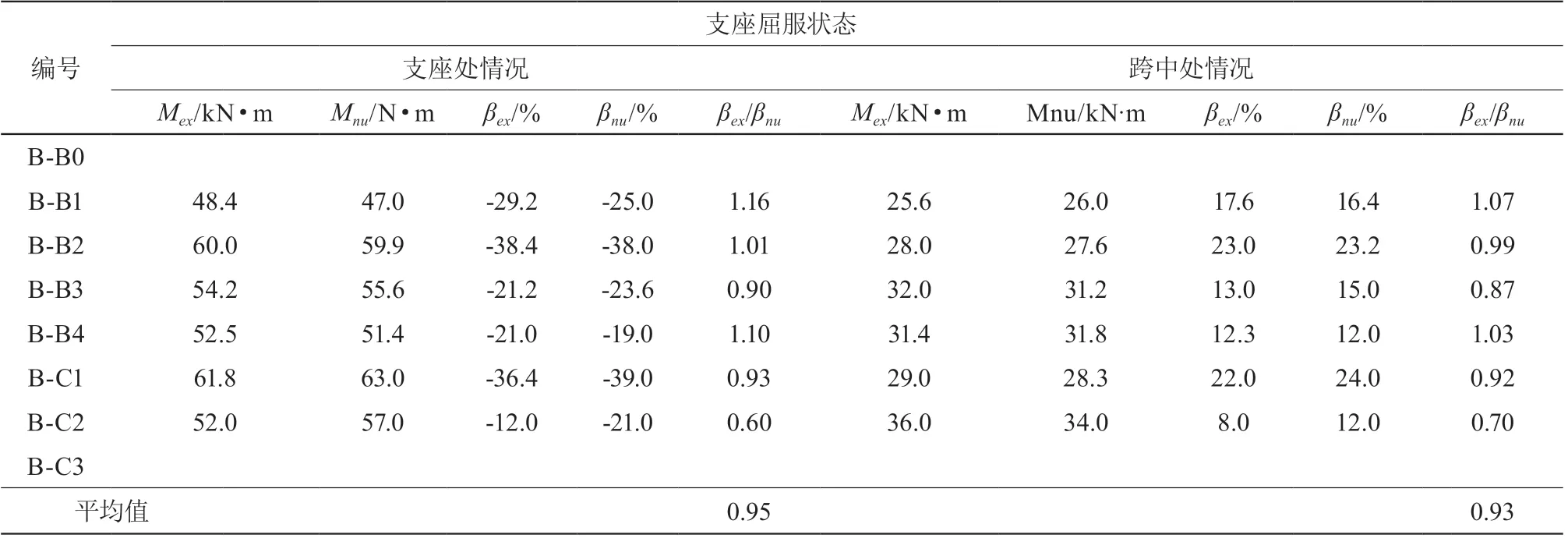
表2 文献［2］～［4］、［18］［19］试验值与理论计算值分析

由表 3 分析，极限状态下构件 B-B0～B-C3 在支座处的的弯矩重分布系数值较为显著，依次为 -12 %、-27.0%、-28.0 %、-10.8 %、-6.8 %、-35.9 %、-14 %、-6.1 %，对应的数值模拟弯矩调幅系数依次为 -21.8 %、-27.7 %、-20.4 %、-10 %、-2.4 %、-36.8 %、-18 %、-5.3 %，模拟结果与实际试验梁的弯矩重分布系数基本吻合，且模拟情况下FRP加固试验梁的弯矩重分布系数随跨中处加固量的增加而减小。构件 B-0～B-3 在支座处的弯矩重分布系数分别是-12.0 %、21.0 %、21.0 %、6.0 %，与之对应数值模拟得到的弯矩重分布系数分别是 -11.0 %，12.0 %、22.0 %、6 %；构件 B-0～B-3 在跨中处的弯矩重分布系数分别是6.0 %、-6.0 %、-19.0 %、-6.0 %，与之对应数值模拟得到的弯矩重分布系数分别是 9.0 %、-6.0 %、-15.0 %、-16.0 %，可知在极限状态下支座与跨中处的试验弯矩重分布系数和数值分析的弯矩重分布系数基本相等。

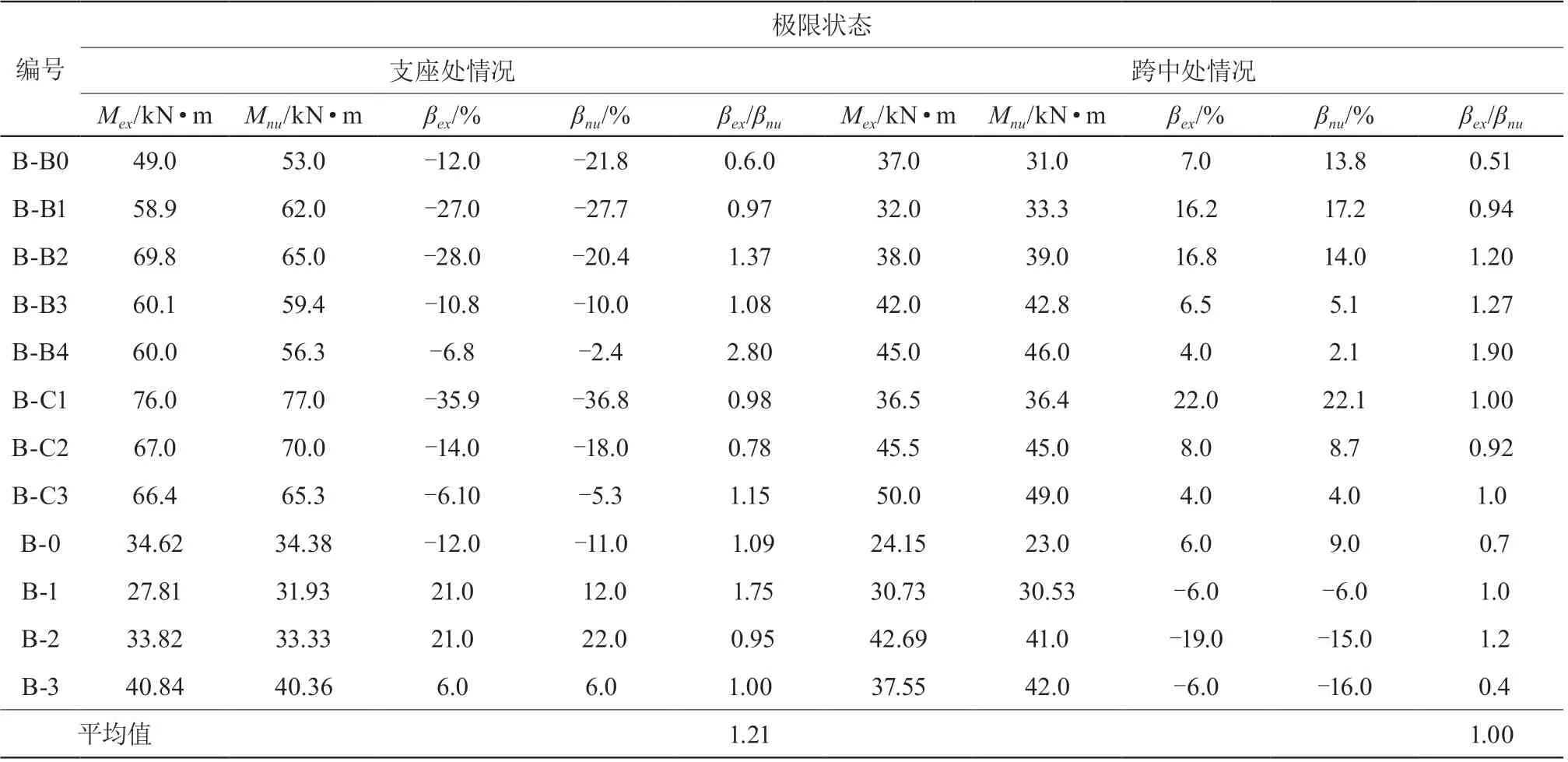
表3 文献［2］～［4］、［18］［19］试验值与理论计算值分析

表 2、表 3 分析得出共性问题，跨中和支座处模拟曲线呈三段变刚度分布曲线，试验下的弯矩重分布系数与模拟分析的弯矩重分布系数相对一致，且变异系数不大，表明数值模拟计算精度较高，纤维材料加固两跨连续梁的弯矩重分布系数的计算公式即适用。

4 模拟梁分析

上述两跨 T 形截面混凝土试验梁在跨中两点加载下模拟结果如表 4 所示。

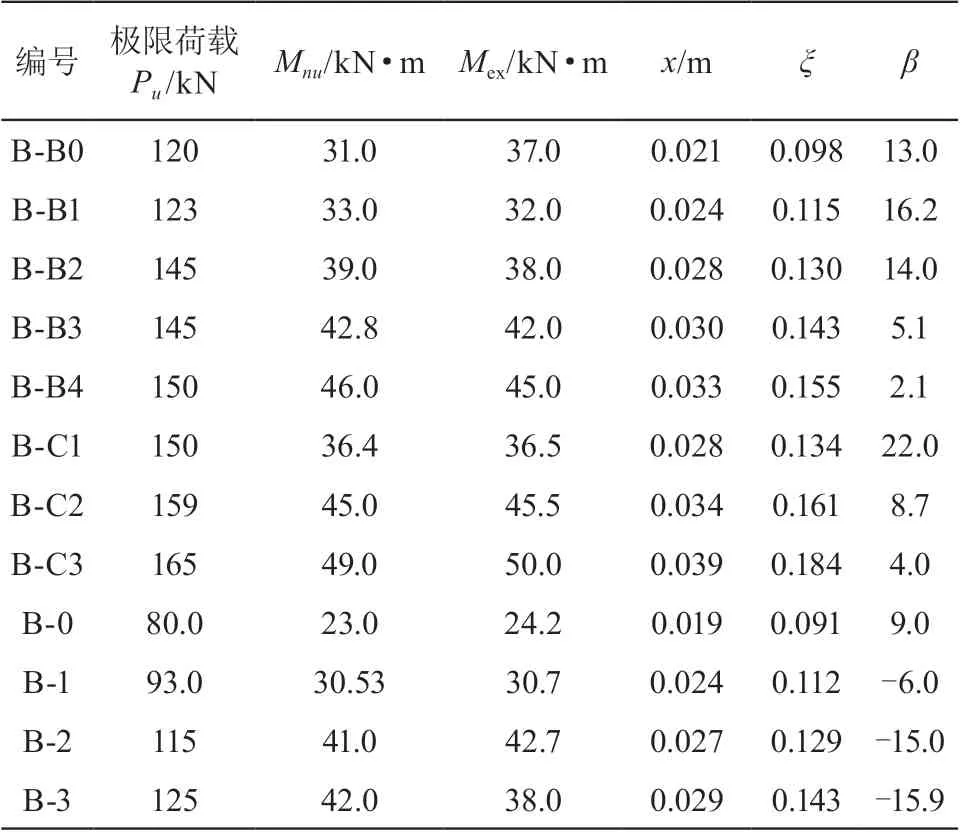
表4 模拟试验梁计算结果

由图 11 可知，数值模拟跨中处的弯矩重分布系数随着截面受压区高度的增大而减小，二者之间可近似呈线性关系，不同的加固材料的弯矩重分布系数与相对受压区高度之间的关系是不同的。

根据弯矩重分布系数β与跨中处截面受压区高度的关系，由图 11-（a）可得 CFRP 加固跨中 0～3 层下的以受压区高度ξ为自变量的跨中处弯矩重分布系数的计算公式见式（6）：

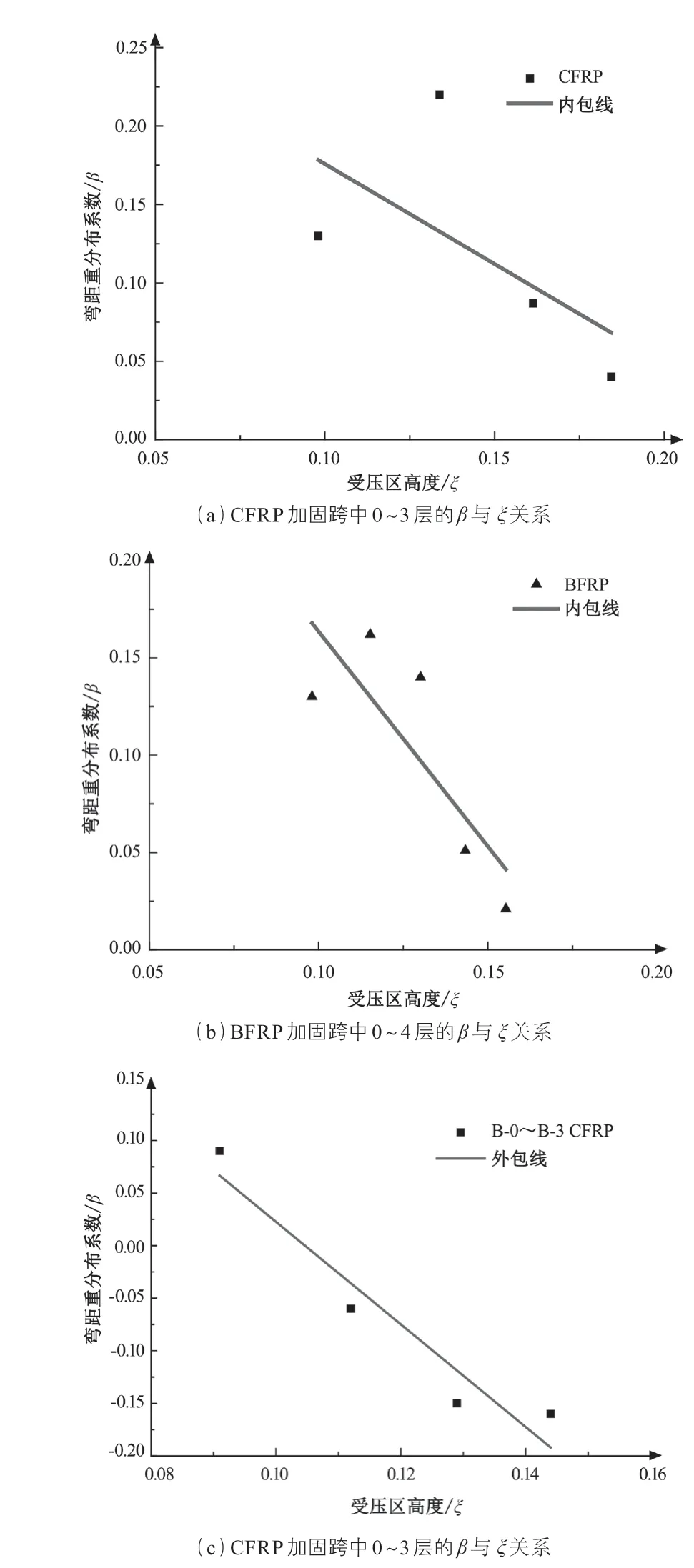
图11 β 与 ξ 的分布关系图

根据弯矩重分布系数β与跨中处截面受压区高度的关系，由图 11-（b）可得 BFRP 加固跨中 0～4 层下的以受压区高度ξ为自变量的跨中处弯矩重分布系数的计算公式见式（7）：

根据弯矩重分布系数β与跨中处截面受压区高度的关系，由图 11-（c）可得 CFRP 加固跨中 0～3 层受压区高度ξ的关系见式（8）：

根据现行规范［20，21］，规定弯矩重分布系数的最高取值为 30 %，由上述模拟数值可知，连续梁的截面相对受压区高度基本控制在 0.1～0.2，截面受压区高度控制在 0.076～0.156 h，并且模拟得到的弯矩重分布系数基本控制在 25 % 范围内。

5 结论

1）既有的分析模型适用于平截面假定条件，试验梁破坏条件主要由受压区混凝土被压碎和 FRP 布被拉断这两部分控制，建立的模拟连续梁可体现截面开裂到截面破坏的发展过程。

2）本文主要数值模拟了 12 根 T 形截面混凝土连续梁的弯矩重分布情况，其弯矩重分布机理主要表现在钢筋屈服荷载和极限荷载，连续梁模拟得到的屈服弯矩和极限弯矩随加固材料的增加而变大，但屈服状态下的截面刚度变化远比极限状态下的截面刚度变化大。

3）以相对受压区高度为自变量计算的弯矩重分布公式，跨中处的弯矩重分布系数与受压区高度线性相关，截面混凝土受压区高度在 0.076～0.156 h，相应的弯矩调幅系数可控制在 25 % 范围内，满足我国现行规范的限值要求，构件安全适用。Q