基于TOPSIS法的老龙头浅埋连拱隧道施工方案优选研究

王景春， 薛佳龙， 霍东辉， 刘超， 马永利

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043； 2.石家庄铁道大学 大型结构健康诊断与控制研究所，河北 石家庄 050043；3.秦皇岛路桥建设开发有限公司，河北 秦皇岛 066000)

1 前言

随着国内外公路网的不断发展和完善，穿越旅游景区的公路隧道逐渐增多。旅游景区隧道施工不仅对地表人文景观建筑产生不同程度的影响，还会对景区环境造成污染。相比分离式隧道，连拱隧道因占地少，路线的选择自由度较大，适应多种复杂地形条件，同时对周围环境影响较小等优势，成为在旅游景区修建隧道时常采用的结构形式[1]。然而，由于连拱隧道施工工序多、开挖和支护交错等缺点，增加了施工过程中变形控制的难度[2]，因此，优选安全经济、环境友好型的施工方案对于旅游景区隧道施工尤为重要。根据隧道所处工程地质条件，连拱隧道常采用中隔壁法、三导洞法、双侧壁导坑法以及微台阶开挖法等施工方案。在隧道施工前期，如何准确合理地确定施工方案是多数连拱隧道工程所面临的技术难题之一。

目前，在隧道施工方案优选研究领域中，大多数研究以不同隧道施工方案对围岩稳定性影响程度不同作为研究对象，进而对隧道施工方案进行优选。比如：Wang Shuren等[3]研究了高应力下软岩隧道施工中两种施工方案的变形效果，并基于力学分析对施工方案优化；Wu Kui等[4]运用FLAC3D比较了4种隧道施工方案对下穿火车站浅埋隧道影响，并确定CRD法为该工程最佳开挖方案；申玉生等[5]运用数值模拟对比分析了不同施工方案引起的浅埋暗挖矩形隧道变形指标及规律，进而确定最优方案；卿伟宸等[6]通过数值模拟和现场监测研究了特大跨度深埋隧道施工中的5种不同开挖方案施工效果等。

以往优选隧道施工方案时缺少对不同隧道施工方案的经济性和环保性进行比选。鉴于此，该文结合旅游景区浅埋连拱隧道施工中要求的安全性、经济性和环保性来建立隧道施工方案优选评价指标体系，并采用博弈论组合赋权法融合评价指标的主客观权重，弥补评价指标赋权过程中主观干扰或完全取决于样本数据的缺陷，同时改进TOPSIS法的不足，从而建立适用于旅游景区浅埋连拱隧道施工方案优选的评价模型。

2 隧道施工方案优选评价指标体系

2.1 评价指标体系的确定

影响旅游景区浅埋连拱隧道施工方案选取的因素众多，构建一套科学合理的评价指标体系是进行旅游景区浅埋连拱隧道施工方案优选的首要前提。由于客观条件的制约，不可能将所有指标都反映到评价中，根据隧道工程经验和文献资料[7]的分析，从施工安全性、工程经济性和环境友好性3个方面入手，本着安全第一，兼顾经济和环保的原则，将安全性、经济性和环保性细分为7项评价指标，构造目标层—准则层—指标层3级体系框架，具体评价指标体系如图1所示。

图1 旅游景区浅埋连拱隧道施工方案优选评价指标体系

2.2 评价指标的量化

在上述7项评价指标中，有些指标可以定量，例如，工程进度、工程造价和地表最大沉降等，可通过工程预算和数值模拟等方法对定量指标进行量化；而其他则为定性指标，为使评价结果客观可靠，必须对定性指标进行量化，参考文献[8]的评判标准，提出隧道施工方案优选评价中定性指标的具体量化评判标准，如表1所示。

表1 定性指标量化评判标准

3 隧道施工方案优选模型

3.1 评价指标综合权重的确定

层次分析法以业内多名专家根据自身经验对评价方案打分为基础，具有主观性强的特点。具体计算步骤参考文献[9]，所得主观权重记作w1=(w11，w12，…，w1n)，n为评价指标数量。

熵权法是根据指标变异性大小求得客观权重，即方案中某个指标变异程度越大，提供的信息量就越多，对隧道施工的影响程度也就越大。但是权重随样本变化而变化，过于依赖样本、忽略指标本身对评价方案重要性影响，计算步骤参考文献[10-11]，所得客观权重记作w2=(w21，w22，…，w2n)。

博弈论组合赋权法[12]是在不同赋权方法所得权重值之间寻求妥协或一致，使指标权重与最优权重偏差最小，从而得到更合理的组合权重。该方法是对不同赋权方法的优化组合，弥补了单一赋权的缺陷，其计算流程如下：

假设采用N种方法对各评价指标赋权，从而得到N个指标权重向量，组成基本权重集W={w1，w2，…，wN}，将这N个权重向量进行任意线性组合：

(1)

式中：w为综合权重向量；αk为权重向量组合系数；wk为第k种赋权方法的权重向量。

优化组合系数αk，使w和各wk的离差极小化，进而获得最优的综合权重向量w*。导出对策模型：

(2)

式(2)最优化1阶导数条件为：

(3)

计算得到权重组合系数(α1，α2，…，αN)，对其进行归一化处理得到(α1*，α2*，…，αN*)，并将其代入式(1)得最优的综合权重向量：

(4)

式中：w*=(w1*，w2*，…，wn*)为n项评价指标最优的综合权重向量；αk*为权重向量组合系数。

3.2 传统的TOPSIS法

逼近理想解排序法(TOPSIS)[13]是一种有限方案多目标决策分析方法，其基本原理是：基于各评价指标实测数据建立决策矩阵，从有限方案中寻找最优方案和最劣方案，用向量表示，并分别求出各方案与它们之间的距离，计算不同方案的相对贴近度，进而做出综合评价。由于其简便、有效，而被广泛应用于解决方案优选问题。计算流程如下：

(1) 建立决策矩阵

建立决策矩阵A=(aij)m×n，i=1，2，…，m；j=1，2，…，n；aij为第i个评价方案的第j个指标值。

(2) 决策矩阵规范化

为排除指标间量纲对评价的影响，需要对决策矩阵进行规范化，得到规范化矩阵B=(bij)m×n，详细的规范化方法如下：

若aij为效益属性指标(越大越优)，则：

(5)

若aij为成本属性指标(越小越优)，则：

(6)

式中：bij为第i个评价方案的第j个指标规范化处理后的指标值；amax、amin分别为同一指标下的最大值、最小值。

(3) 规范化决策矩阵加权

(7)

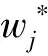
(4) 确定正、负理想解

设正理想方案向量为：v+=(v1+，v2+，…，vn+)T；负理想方案向量为：v-=(v1-，v2-，…，vn-)T。在m个方案中，其计算方法如下：

vj+=[maxvij]，i=1,2,…,m；j=1,2，…,n

(8)

vj-=[minvij]，i=1,2,…,m；j=1,2，…,n

(9)

式中：vj+和vj-分别为第j个评价指标的正负理想解。

(5) 计算距离

通过欧氏距离求得第i个方案到正负理想解的距离di+和di-：

(10)

(11)

(6) 计算不同方案的相对贴近度Ci

Ci=di-/(di++di-)

(12)

依据Ci值大小对备选方案排序，Ci越大，方案越优。

但是，当隧道施工方案优选评价指标体系中存在两个或多个线性相关指标时，它们组成的列向量不能成为决策矩阵的基向量，而欧式距离未考虑到评价指标的相关性，这样便使运用欧式距离计算所得结果不再可靠。另外，仅以距离计算各个方案的贴近度只能表明评价方案与最优和最劣方案在数据曲线上的位置关系，不能表现出其曲线形状变化，导致当评价方案与最优和最劣方案在平面位置的距离相近时，即便曲线态势相差较大也会造成评价结果相近的情况。评价指标之间的相关性无法计算以及贴近度计算方法单一是传统TOPSIS法多指标多方案综合评价中存在的不足。针对这两点缺陷，该文分别采用马氏距离和灰色关联度对TOPSIS法进行改进，使TOPSIS法在旅游景区浅埋连拱隧道施工方案优选评价中得到更科学合理的应用。

3.3 改进的TOPSIS法

与欧氏距离相对应的马氏距离可以有效解决评价指标之间线性相关的计算问题，其计算公式为：

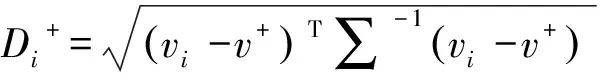
(13)

(14)

由式(13)、(14)可知：若评价指标间相互独立，则马氏距离等同于加权的欧氏距离，权重为各评价指标标准差的倒数。因此，相比欧氏距离，马氏距离更具有灵活性，可有效解决传统TOPSIS法在多指标多方案综合评价中若评价指标之间存在相关，则欧氏距离失效的问题。

灰色关联度[14-15]是用有限数列替代无限空间问题，依据有限数列的可比性可以将各数列间的相关程度进行量化和比较分析。若样本数列与理想方案数列的相似程度越大，则样本与理想方案的灰色关联度越大，即样本越接近理想方案。其计算公式为：

(15)

(16)

式中：rij+和rij-为两数列对应评价指标值的灰色关联系数；Δij+=|vij-vj+|和Δij-=|vij-vj-|分别为正负差序列；ζ为分辨系数，一般为0.5；vj+、vj-分别为第j个正理想解、负理想解。

则灰色关联度Ri+和Ri-为：

Ri+={ri+|i=1,2,…,m}

(17)

Ri—={ri-|i=1,2,…,m}

(18)

根据上述计算结果，将Di+、Di-与Ri+、Ri-进行单位统一简化后，第i个评价方案与正负理想解向量v+、v-的合成贴近度分别为：

Li+=β1·Di-+β2·Ri+，i=1，2，…，m

(19)

Li-=β1·Di++β2·Ri-，i=1，2，…，m

(20)

式中：Li+、Li-为合成贴近度；β1、β2为主观因素对评估对象的影响系数，一般主观因素认为两者影响程度相同，即β1=β2=0.5。

相对贴近度Ci*为：

(21)

基于马氏距离和灰色关联度的改进TOPSIS法既解决了对于评价指标具有相关性时，欧氏距离的失效问题，又可准确反映出各评价方案与最优和最劣方案之间的位置关系和曲线态势的差异，使优选结果更加合理可靠。

4 工程实例分析

以河北省秦皇岛市老龙头隧道实测资料为样本数据，采用上述基于改进TOPSIS法的旅游景区浅埋连拱隧道施工方案优选模型为该隧道确定最优施工方案。

4.1 工程概况

老龙头隧道位于河北省秦皇岛市山海关老龙头景区，地处旅游景区且下穿老龙头长城。隧道范围为K1+500～K1+930，全长430 m，并在K1+740处与老龙头长城垂直相交，隧道上方长城存在30 m缺口。隧道埋深为3.3～4.2 m，属超浅埋隧道，设计为连拱双向四车道一级公路隧道。隧道呈东西走向，经过区段为山前丘陵区，区内地形起伏不大，隧道区内未见泉水，地下水埋深4.5～8.5 m。地表层为粉质黏土及砂砾石土，开挖层为强风化花岗变粒岩，围岩较为破碎，按相关规范确定为Ⅴ级围岩，围岩自稳能力较差。因此，本着“安全第一”的原则，在老龙头隧道施工方案选取中主要考虑中隔壁法、三导洞法和双侧壁导坑法，3种隧道施工方案开挖工序与支护结构如图2所示。

图2 3种隧道施工方案图

在上述3种隧道施工方案中，中隔壁法分块少，对围岩扰动程度较低，工程进度快，工程造价低，对周围环境影响小，但支护强度较低，从而引起地表沉降增加，后期运营维护成本随之增加；三导洞法虽然施工工序增加，对围岩扰动程度较高，但每个分块都是在开挖后立即各自闭合，支护强度较高，地表沉降和运营成本随之减小，施工进度和工程造价较为合理，隧道施工对周围环境的影响程度也在可控范围内；双侧壁导坑法虽然支护强度最大，地表沉降最小，后期运营成本最小，但是开挖断面分块多，对围岩扰动大，所以工程进度缓慢，工程造价最大，对周围环境的影响也最高。

4.2 3种施工方案的评价指标量化

根据表1对扰动围岩程度、支护强度、运营成本和周围环境污染程度等定性指标进行量化，结合老龙头隧道的地勘资料、工程造价、施工组织以及数值模拟等资料对工程进度、工程造价和地表最大沉降进行量化，得到各施工方案所对应评价指标的量化结果，如表2所示。由表2可以看出：各评价指标之间存在较强的相关性，显然在隧道施工方案优选过程中再采用基于欧氏距离的传统TOPSIS法已无法进行合理评价。

表2 3种隧道施工方案评价指标量化结果

4.3 综合权重值的确定

采用层次分析法(AHP)确定主观权重，组织隧道工程领域专家学者对各评价指标的重要性进行打分，建立判断矩阵P为：

求得判断矩阵P的最大特征值λmax=8.35，并且满足一致性检验。将特征向量进行归一化处理得到主观权重向量为：w1=(0.210 5，0.184 1，0.157 8，0.131 5，0.052 6，0.184 1，0.078 9)。

采用熵权法确定评价指标的客观权重，构造决策矩阵A为：

计算得客观权重向量为：w2=(0.226 4，0.188 7，0.150 9，0.113 2，0.037 7，0.207 5，0.075 5)。

根据博弈论组合赋权法式(1)～(3)，得到权重组合系数α1=0.653 4，α2=0.726 6，并对其归一化可得α1*=0.473 5，α2*=0.526 5。将主客观权重向量和归一化组合权重系数代入式(4)确定各个评价指标综合权重向量为：w*=(0.218 9，0.186 5，0.154 2，0.121 9，0.044 8，0.196 4，0.077 1)。

4.4 改进的TOPSIS法计算过程

(1)构造加权规范化决策矩阵

利用式(5)～(7)求解老龙头隧道施工方案优选的加权规范化决策矩阵为：

V=

(2) 确定正、负理想解方案

在3个老龙头隧道施工方案中，通过式(8)～(9)确定正理想方案为：v+=(0.140 0，0.138 5，0.099 9，0.079 9，0.034 4，0.153 4，0.059 2)；负理想方案为：v-=(0.093 3，0.069 3，0.078 0，0.575 0，0.017 2，0.076 7，0.029 6)。

(3) 计算马氏距离和灰色关联度

根据式(13)～(18)分别计算出3种隧道施工方案与最优和最劣方案之间的马氏距离和灰色关联度，结果如表3所示。

表3 3种隧道施工方案的马氏距离和灰色关联度

(4) 计算贴近度

根据贴近度计算公式(19)～(21)，得到3种隧道施工方案的合成贴近度和相对贴近度见表4。

表4 3种隧道施工方案的贴近度及排序

由表4可知：在老龙头隧道中，3种施工方案中优劣顺序依次为：三导洞法最优，双侧壁导坑法次之，中隔壁法最差。

综上所述，三导洞法施工虽然对老龙头长城及围岩影响并不是最小的施工方案，但该施工方案控制老龙头长城和围岩变形能力较好，隧道和长城变形在安全可控范围内，并且工程造价合理，避免了对建筑材料的浪费，在老龙头景区采用三导洞法施工也可减小对周围环境的影响。老龙头隧道实际工程中采用三导洞法施工在安全性、经济性和环保性上实现了工程效益的最大化，客观地反映了旅游景区浅埋连拱隧道施工方案优选模型在隧道施工方案优选领域的可行性和有效性。

5 结论与讨论

该文针对选择旅游景区浅埋连拱隧道最优施工方案的问题，建立了隧道施工方案优选模型，并将该模型应用于老龙头隧道施工方案选取，得到以下结论：

(1) 针对以往隧道施工方案优选中指标选取单一的问题，该文综合考虑了旅游景区浅埋连拱隧道施工方案中安全、经济和环境的因素，建立了更全面的旅游景区浅埋连拱隧道施工方案优选评价指标体系。

(2) 针对传统TOPSIS评价方法中存在的缺陷和不足，该文分别采用马氏距离和灰色关联度对其改进，并建立了基于博弈论组合赋权和改进TOPSIS法的旅游景区浅埋连拱隧道施工方案优选模型，为该领域研究提供了一条新的途径。

(3) 工程应用表明：在老龙头隧道工程中，三导洞法在隧道施工的安全性、经济性和环保性综合方面优于另外两种方案。依据分析结果可为决策者在旅游景区浅埋连拱隧道施工方案优选上提供一种理论依据。

基于TOPSIS法建立的旅游景区浅埋连拱隧道施工方案优选模型在老龙头隧道工程应用中选取三导洞法作为其最优施工方案，实际操作中也取得了很好的效果。但是，在确定具体施工方案后，如何协调隧道施工中安全性、经济性和环保性三者之间的关系，即如何对三者统筹规划，进而实现工程效益最大化还需后续针对各评价指标做出更具体及更全面的研究。