PPC斜拉桥模型疲劳试验及塑性损伤分析

2022-05-13袁明谭龙田颜东煌刘昀

中外公路 2022年2期

袁明，谭龙田，颜东煌，刘昀

(1.长沙理工大学土木工程学院，湖南长沙 410114； 2.湖南交通职业技术学院路桥工程学院，湖南长沙 410132)

1 引言

材料疲劳现象是指在外循坏荷载作用下金属材料发生的内部性质改变，反映到宏观得到相关特质的变化[1]。现有桥梁不仅承受单一不变的恒荷载，更多的是需要承受往复循环的活荷载，就破坏形态而言，疲劳破坏是最重要的形态之一，且疲劳破坏多发生在其最大循环荷载小于静载极限强度的状态下。

斜拉桥是一种桥面体系受压，支承体系受拉的桥梁。其桥面体系用加劲梁构成，其支承体系由钢索组成[2]。混凝土斜拉桥是指加劲梁由混凝土制成，如今混凝土斜拉桥加劲梁大多选用全预应力设计，在运营阶段过多的预应力束反而成为了负担，且过大的压应力会降低斜拉桥的安全性[3]。

部分预应力混凝土(PPC)桥梁是指在荷载频遇组合下控制的正截面受拉边缘出现拉应力或出现不超过规定宽度的裂缝。部分预应力材料经济，可以节约大量预应力钢筋并优化锚固点集中区的构造，使施工中张拉锚固等工序更简便，节约夹锚具等[3]；李忠诚、于琦等[4-5]从钢筋应力与混凝土受拉边缘名义拉应力两个角度对部分预应力梁的裂缝宽度控制计算，对主梁的部分预应力设计提供了设计依据；卢树圣[6]建议考虑动载时的铁路桥梁部分预应力混凝土A、B类构件的分类限值；王永强等[7]考虑部分预应力混凝土梁裂缝闭合的性能，提出了卸载系数的概念并对裂缝宽度控制计算进行了相关研究；韩基刚等[8]在研究中考虑了非预应力钢筋与混凝土的黏结应力-滑移退化关系，建立了部分预应力混凝土梁疲劳中的裂缝扩展计算模型，并对该计算模型进行了试验验证；颜东煌、刘昀等[9-11]完成了全预应力斜拉桥的缩尺模型设计，进行了相关斜拉桥缩尺模型静载试验和数值模拟，并对部分预应力斜拉桥设计的合理性进行了分析以及相应的计算。

目前，对部分预应力混凝土桥梁静载性能与疲劳性能的研究大部分是基于梁桥体系，而混凝土斜拉桥作为在实际工程中200～400 m的跨径下非常具有竞争力的桥型[12]，部分预应力混凝土在斜拉桥体系中应用的研究却很少，且在中国已施工完成的混凝土斜拉桥中加劲梁大部分采用了全预应力设计[13]。为了对部分预应力混凝土在斜拉桥体系中的应用进行进一步的研究，该文在课题组前期研究的基础上，以某座主跨220 m的斜拉桥为背景，制作比例缩尺模型，对加劲梁进行B类部分预应力设计，并进行静载与疲劳试验；使用Abaqus软件建立缩尺模型有限元模型，在混凝土材料属性中引入损伤因子用于拟合混凝土的弹塑性性质，从而对加劲梁在加载中所产生的损伤进行模拟，并将有限元计算结果与试验数据进行对比分析。

2 试验概况

2.1 试验梁构造

某PC斜拉桥，跨径为(110+220+110) m，桥型布置如图1所示。选取图1中5个索段，根据相似理论[9]，制作相似比为1∶7.4的缩尺模型为试验梁。试验梁全长7.2 m，主梁模型尺寸如表1所示。主梁混凝土标号为C50，纵筋采用直径8 mm与10 mm的HRB335钢筋，箍筋采用直径8 mm的HRB335钢筋，预应力筋与斜拉索采用1×7钢绞线，公称直径15.2 mm，主梁横截面图及配筋如图2所示。主梁内埋置高强螺杆与斜拉索连接，试验前进行28 d养护使其达到强度。

图1 桥型布置图(单位：cm)

表1 主梁模型尺寸图

图2 主梁横截面及配筋图(单位：cm)

2.2 索力与预应力设置

试验梁通过索力与预应力控制达到部分预应力B类构件设计，其索力大小及预应力大小如表2所示。成桥状态基于最小弯曲能量法进行调索[14]，使试验梁的恒载弯矩处在一个比较合理的状态。在索力与预应力作用下，主梁跨中截面底缘压应力为3 MPa，在1.4倍车道荷载作用时主梁跨中截面底缘出现2.9 MPa拉应力，混凝土发生初裂，设计满足B类预应力在荷载频遇组合下受拉边缘出现不超过限制宽度裂缝的要求。车道荷载由实桥荷载等效所得，实桥荷载等级为公路-Ⅰ级，试验梁根据相似比等效后1倍车道荷载集中力为10.82 kN，均布力为2.35 kN/m。

表2 斜拉索索力及预应力筋预应力大小

2.3 荷载加载方案

由实桥荷载谱计算得其受拉区边缘应力幅为3.0 MPa，疲劳荷载值的选取采用与实桥应力幅等效原则，在考虑到疲劳加载中的恒载惯性力后，所选取的疲劳荷载与停机静载参数如表3所示，在疲劳荷载上峰值与下峰值时受拉区边缘主应力分别为1.52、-1.30 MPa，疲劳荷载作用频率为1.5 Hz。疲劳荷载根据GB 50152—92[15]相关规定采用正弦波加载，试验加载频率为1.5 Hz，试验总疲劳次数为750万次，将其分为主梁无损伤时250万次，主梁0.1 mm裂缝损伤时250万次，主梁0.2 mm裂缝损伤时250万次。在疲劳荷载加至1万、2万、10万、20万、50万、100万、120万、150万、180万、210万、250万次时暂停疲劳加载，进行静载试验测试关心截面的挠度及索力变化，重复2～3次取平均值。

在工况Ⅰ与工况Ⅱ之间通过静力荷载使主梁出现0.1 mm裂缝，在工况Ⅱ与工况Ⅲ之间通过静力荷载使主梁裂缝发展到0.2 mm。

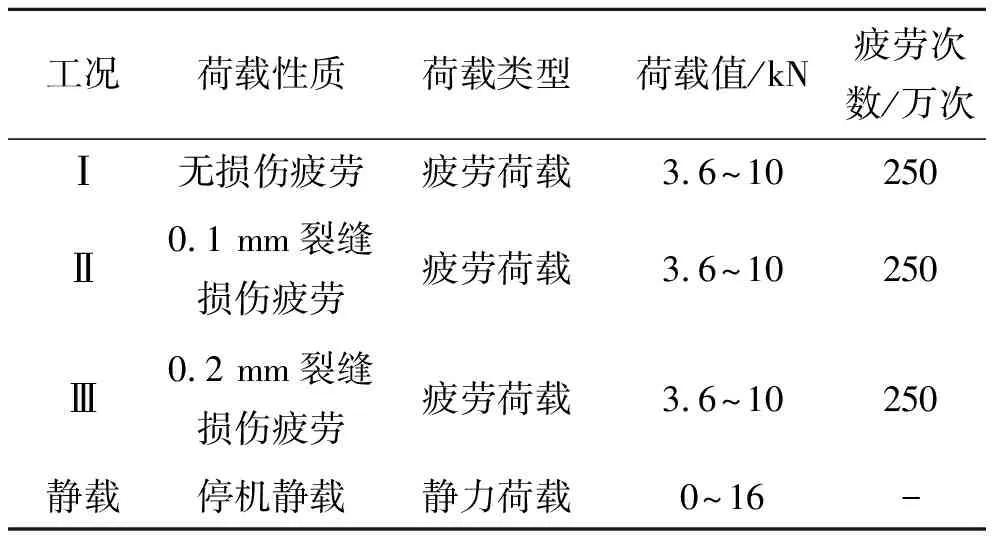
表3 疲劳荷载参数

2.4 试验数据采集

在两端弹簧支座、跨中、1/4跨与3/4跨处以及每根斜拉索的下方和相邻斜拉索中点处共布有13个位移传感器，记录疲劳过程中的位移与静载加载试验中的荷载-挠度曲线。5根斜拉索的索力采用20 t穿心式振弦锚索计进行测量，记录每次静载加载中斜拉索的索力变化量。使用DH3822施工状态监测系统对疲劳加载过程中混凝土底板动态应变进行监测，以对疲劳荷载进行控制。总体布置图如图3所示。

图3 总体布置图

3 试验结果及分析

3.1 主梁挠度试验结果

选取试验梁跨中截面为关心截面，对其在每次停机静载试验中的位移进行分析。各疲劳工况下停机静载试验中跨中截面在最大荷载下的位移如图4所示。

由图4可知：各疲劳荷载工况下主梁位移随着疲劳次数的增加都有所增大，在工况Ⅲ的210 万次疲劳荷载后的停机静载中主梁位移出现最大值3.06 mm。通过对数型回归方程计算，工况Ⅰ～Ⅲ下主梁位移增量分别约为0.093、0.105、0.141 mm，由此可看出：由于初始损伤的不同，各工况下主梁位移增量也有所不同，即初始损伤越大，疲劳荷载所造成的位移增量也更大。在工况Ⅰ～Ⅲ中150万次疲劳荷载后的停机静载中，主梁的位移分别为2.26、2.69、2.95 mm，对3个工况中相同疲劳次数后的主梁位移进行对比，可知初始损伤越大，位移的绝对值也有所增加。相对于初始损伤增大所带来的位移增量，在各工况中主梁位移的增量较小。在停机静载中主梁均未出现不可恢复位移，故在试验荷载作用下损伤的发展也较为缓慢。

图4 工况Ⅰ～Ⅲ位移图

3.2 主梁裂缝试验结果

在工况Ⅰ与Ⅱ、工况Ⅱ与Ⅲ之间的两次静载试验中，测得1.79倍车道荷载时主梁底板出现裂缝，2.50倍车道荷载时裂缝宽度达到0.1 mm，在3.22倍车道荷载时裂缝宽度达到0.2 mm，在卸载后裂缝均闭合。主梁裂缝均匀分布在集中荷载加载点两侧，各级车道荷载下裂缝分布如图5所示。在工况Ⅱ与Ⅲ中，由于预应力与索力的作用，未出现裂缝在荷载作用下的张合，故裂缝闭合较好，且通过仪器观测裂缝也未出现可见发展。

3.3 索力试验结果

选取试验梁跨中截面对应的12#索，对其在每次停机静载试验中的索力增量进行分析。各疲劳工况停机静载试验中12#索索力增量在最大荷载下的位移如图6所示。

由图6可知：在各疲劳工况，停机静载时索力的增量变化不大且无明显差异，均处于1.5～2 kN，索力最大增量2 kN出现在工况Ⅱ的10万与50万次停机静载中。在静载加载过程中索力增量随着分级加载呈现近似的线性增长，且加卸载时索力的变化曲线也较为吻合，表明试验梁中斜拉索的抗疲劳性能较为优越。

图5 主梁裂缝分布图(单位:cm)

图6 工况Ⅰ～Ⅲ作用下12#索索力增量图

4 有限元模型模拟

4.1 材料参数

4.2 混凝土静载本构模型

该文参考GB 50010—2010《混凝土结构设计规范》[18](简称《规范》)给定的混凝土静载本构模型进行静载损伤因子的计算，无量纲处理后的单轴受拉应力-应变曲线方程为：

(1)

单轴受压应力-应变曲线方程为：

(2)

式中：αa、αt、αd取值可由《规范》表C.2.1确定。由能量等价原理得无损伤混凝土弹性余能为：

(3)

考虑混凝土损伤弹性余能为：

(4)

(5)

由Ed=E0(1-d)2可得：

σ=E0(1-d)2ε

(6)

将式(1)、(2)代入式(6)，可以得到单轴受拉与受压损伤因子分别为：

(7)

dc=

(8)

4.3 混凝土疲劳本构模型

疲劳本构模型通过疲劳剩余强度包络线进行计算，疲劳剩余强度包络线是指在循环荷载作用下材料疲劳剩余强度与疲劳次数的关系。混凝土疲劳剩余强度包络线如图7所示，设循环荷载第n次作用时混凝土最大应力、应变与包络线的交点为(εc,fat，fc,fat)，且将疲劳荷载作用下的受压应力-应变曲线的下降段近似认为与静力荷载作用下曲线的下降段相同。考虑混凝土在疲劳加载过程中，承受的压应力相对于静载极限强度较小，则(εc,fat，fc,fat)可按下述方程求得:

(9)