机场刚性道面基层顶面模量转换关系研究

董倩, 吕耀志, 程少锋， 张献民

(1.中国民航大学 机场学院, 天津市 300300； 2.天津市市政工程设计研究院， 天津市 300051；3.天津市基础设施耐久性企业重点实验室，天津市 300051)

目前，中国刚性水泥混凝土道面设计中由基层顶面反应模量计算道面的刚度半径，进而确定面板厚度。而基层顶面反应模量由土基反应模量和基层当量厚度查经验图确定，其中基层当量厚度值由基层各材料层的厚度乘以其相应的当量系数相加而得[1]。但当量系数以区间形式列出，且未明确规定当量系数与材料强度的一一对应关系，需根据经验选取，导致此方法确定的基层顶面反应模量误差较大，从而影响了道面设计的准确性。

在弹性层状体系理论下，基层顶面回弹模量与基层顶面反应模量具有相似意义，它表征面层以下各结构层对于面层的支承作用，通常由面层以下各结构层弹性模量与厚度通过特定方法计算得出。关于基层顶面回弹模量的确定方法已有深入研究，研究成果颇为成熟。总体分为两类：基于弯沉等效[2-5]或基于应力等效[6-8]，如王振辉、蔡良才等[2]基于位移等效原则，研究了道面结构参数、飞机荷载作用半径及主起落架构型对基层顶面当量回弹模量的影响，建立了机场道面基层顶面当量回弹模量的回归公式；姜爱锋、姚祖康[5]指出现行水泥混凝土路面设计规范中在多层弹性地基模量换算方面存在的问题，给出了目前常用路面结构形式下切实可行的解决办法；蒋应军等[7]应用弹性层状理论，研究了不同等效方法对基层顶面当量回弹模量换算结果的影响，确定了不同等效方法的适用条件。

该文提出由机场水泥混凝土道面基层顶面回弹模量确定反应模量的方法。基于弯沉等效原则，依托有限元模拟计算，通过设计正交试验，研究基层顶面反应模量与基层顶面回弹模量间的转换关系，建立回归公式。当道面面层以下各结构层参数确定后，首先转换成基顶回弹模量[2]，然后根据转换关系，精确确定反应模量，为机场水泥混凝土道面结构层设计及PCN计算提供方便。

1 模量换算原理与方法

关于反应模量与回弹模量的转换研究，国内外研究并不多见。张建霖等[9]依据实测点挠度相等的方法实现地基回弹模量和反应模量之间的转换；尚世英等[10]利用最小二乘准则，并利用特定点位置位移相等，实现两种模量的转换。然而，两种地基理论下的位移表达式复杂，上述专家提供的模量转换方法，需要借助计算机迭代运算确定两个地基参数，实际应用过程中难度较大。FAA在提出刚性道面设计建议时，给出了回弹模量与反应模量转换的经验公式[11]，但此类方法并未考虑面层参数对转换关系的影响；唐亨山、张海泉[12]根据现场承载板试验实测数据，给出了软黏土路基上土基回弹模量与地基反应模量间的回归关系，但其通用性受到限制。该文建立的模量转换关系模型基于位移等效原则，即荷载作用位置处位移相等，考虑了典型的刚性道面结构，通用性强，具体原理如下：

Winkler地基条件下，圆形均布荷载p作用时，水泥混凝土道面板产生的挠度如式(1)所示：

(1)

弹性半空间地基条件下，圆形均布荷载p作用时，道面板产生的挠度如式(2)所示：

(2)

式中：kj、E0、μ0分别为基顶反应模量、回弹模量、泊松比；R为荷载圆半径；Q为均布荷载合力；t为积分参数;l为道面板的相对刚度系数;a为道面板的弹性特征系数。

l、a分别如式(3)、(4)所示：

(3)

(4)

式中：E、μ、h分别为道面板弹性模量、泊松比、厚度；J0、J1分别为第一类零阶、一阶贝塞尔函数。

当地基反应模量与回弹模量给定时，便可以通过式(1)～(4)计算出特定点的挠度值。根据位移等效原则，令荷载作用位置中心点的位移相等，即wA(r)=wB(r)，且Q=q·πR2，则有：

(5)

(6)

如此便建立了基顶反应模量与回弹模量的转换。但l中含有kj，a中含有E0，转换过程中涉及迭代运算，计算繁琐。因而通过有限元模拟不同道面结构，计算一一对应的反应模量与回弹模量，通过多元非线性拟合，确定二者的转换关系。

2 有限元模型的建立与精度验证

有限元模型计算精度的高低是基层顶面反应模量与回弹模量能否精确转换的基础。首先对建立的有限元模型进行精度验证[13]。分别计算集中荷载与均布荷载作用下，有限元解与理论数值解的误差，调整有限元网格、边界条件等参数，直至有限元解与理论数值解的误差在10%以内。

2.1 弹性半空间地基

弹性半空间体地基模型中，场道面层尺寸为45 m×15 m×0.36 m(宽×长×厚)，有限元单元体尺寸0.3 m(宽)×0.15 m(长)×0.18 m(厚)，由实体单元Solid 45模拟。弹性半空间体地基假设土基在厚度方向无限延伸，考虑计算机的运算速度，且由土基附加应力与自重应力的比值小于5%[14]确定有限元模型的土基厚度为12 m，土基网格尺寸划分为0.3 m(宽)×0.15 m(长)×0.5 m(厚)。所建立的模型坐标系统中，Z方向为飞机滑行方向，X方向为垂直于飞机滑行方向，Y方向为道面结构的竖直方向。道面板四边自由，不施加约束；基层部分垂直于飞机滑行边界(XOZ平面)，施加X、Y、Z3个方向约束，平行于飞机滑行方向的边界(YOZ平面)，施加X方向约束，底面施加全约束[15]。半径为0.15 m，胎压为1.15 MPa均布荷载作用下，理论数值解与有限元解的误差如表1所示。由表1可以看出：大多误差控制在5%以内，因此模型精度符合要求。

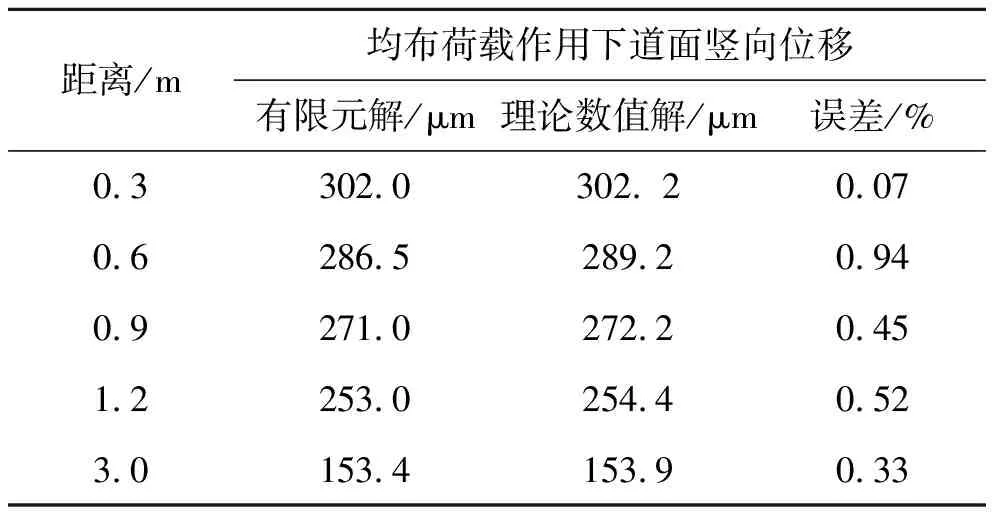
表1 弹性半空间地基位移误差

2.2 文克勒地基

Winkler地基板系统的面板尺寸、网格划分、模拟单元、强度参数均与弹性半空间地基相同。Winkler地基由Combine14模拟，弹簧刚度由基顶反应模量与网格尺寸依照贡献面积法[17]获取。水泥混凝土道面板四周自由，仅在板底面的四边施加全约束，弹簧底端施加全约束。分别计算在集中力和圆形均布荷载作用下，道面的竖向位移，结果如表2所示。由表2可见，位移误差在7%以内。

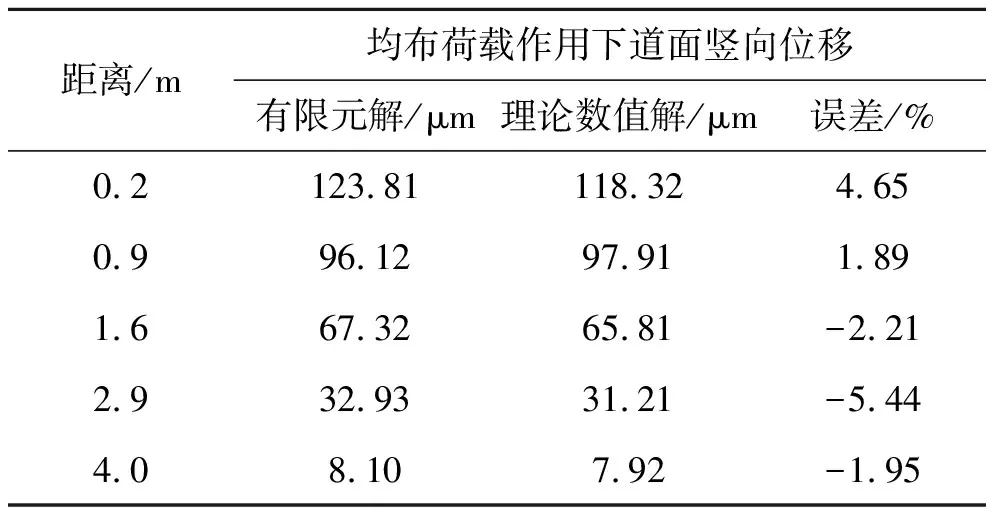
表2 Winkler地基位移误差

3 反应模量与回弹模量转换

3.1 模量转换方法介绍

模量转换基于弯沉等效原则，具体实现过程如下：首先，建立具有一定基顶回弹模量的弹性半空间地基跑道有限元模型，计算其在集中与均布荷载作用下的位移；然后建立具有同样面层结构的Winkler地基模型，施加同样大小的荷载，通过调整反应模量，使荷载作用位置处的竖向位移相等。如此，便确定了与回弹模量对应的反应模量。计算可知，面层厚度为0.36 m，弹性模量为36 000 MPa，基层顶面回弹模量为270 MPa时，对应的基层顶面反应模量为80 MN/m3。距荷载作用中心位置1.2 m及6 m内，道面的弯沉曲线如图1所示。由图1可以看出：两种有限元模型的位移曲线只在荷载作用区或接近荷载作用区较好拟合，距离荷载作用区较远处，位移相差较大，这恰是由于弹性半空间地基模型考虑了土体传递剪力，而Winkler地基模型假设地基不传递剪力所致。

3.2 面层厚度对转换关系的影响

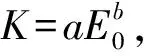
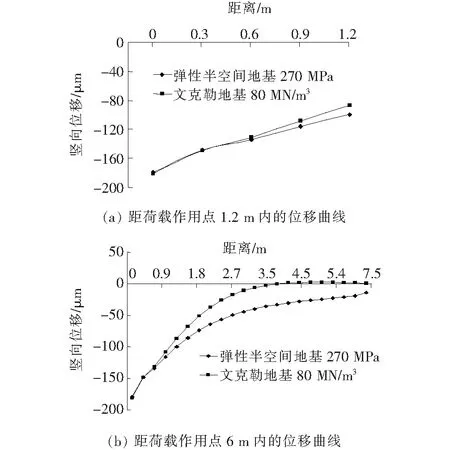
图1 两种地基模型的位移曲线

表3 不同面层厚度下反应模量与回弹模量

3.3 面层弹性模量的变化对转换关系的影响

面层厚度为0.36 m，面层弹性模量为21 000、26 000、29 000、31 000、34 000、37 000 与41 000 MPa时，经有限元计算可得，基层顶面回弹模量E0与反应模量kj转换关系如表4示。由表4可知:基层顶面回弹模量固定不变时，面层弹性模量增大，与之对应的基层顶面反应模量减小。经计算可知：当面层弹性模量由21 000 MPa增大至41 000 MPa时，基层顶面反应模量减幅均为20%左右，说明与面层厚度相比，其弹性模量对转换关系的影响要弱。不同面层模量下，两者呈幂函数关系。

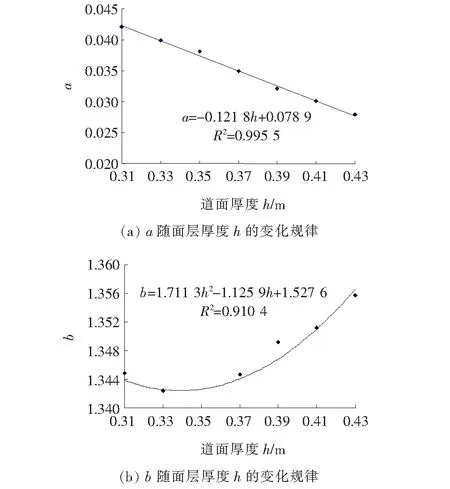
图2 参数a与b 随面层厚度h的变化规律

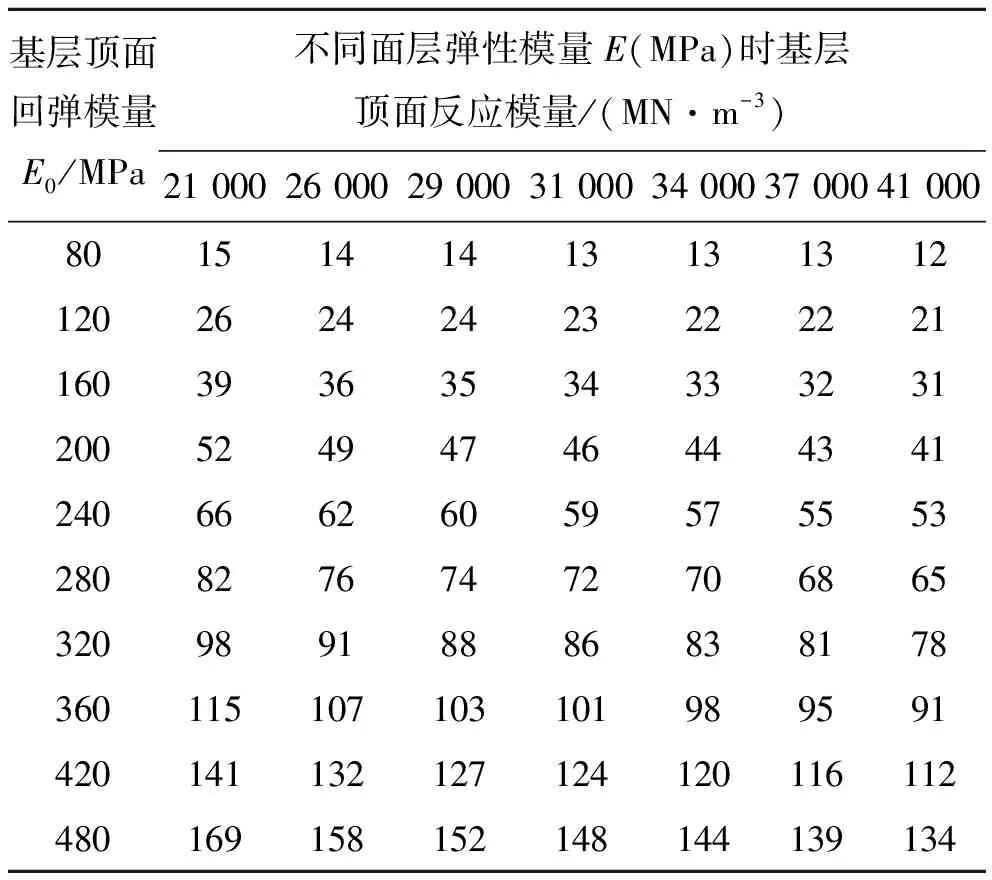
表4 不同面层弹性模量下反应模量与回弹模量

3.4 正交试验法确定模量转换关系

参照上述转换关系确定方法，计算不同刚性面层加铺于各强度的基层结构时，基层顶面回弹模量与反应模量的一一对应值。进行正交试验设计[18]，并开展极差分析，确定显著影响因素。与此同时利用Matlab编程，对大量数据进行多元非线性拟合，即可获得基顶回弹模量与基顶反应模量的转换关系模型。

在进行正交试验设计时，以基层顶面反应模量为试验指标，按照面层弹性模量、厚度、基层顶面当量回弹模量这3个因素的取值范围，设计了L49(75)正交表。因素水平见表5，正交试验方案及结果见表6。

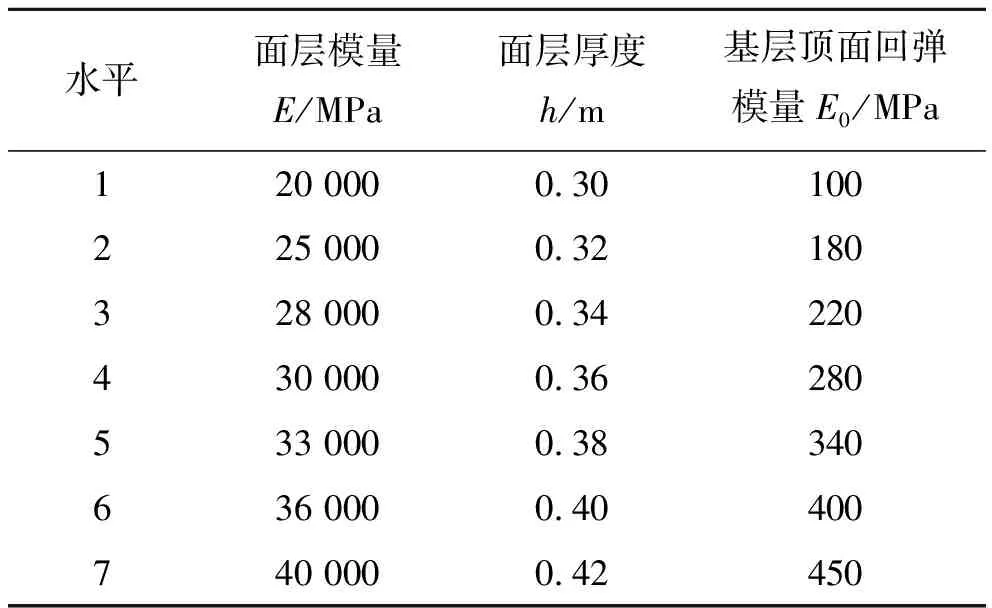
表5 因素水平

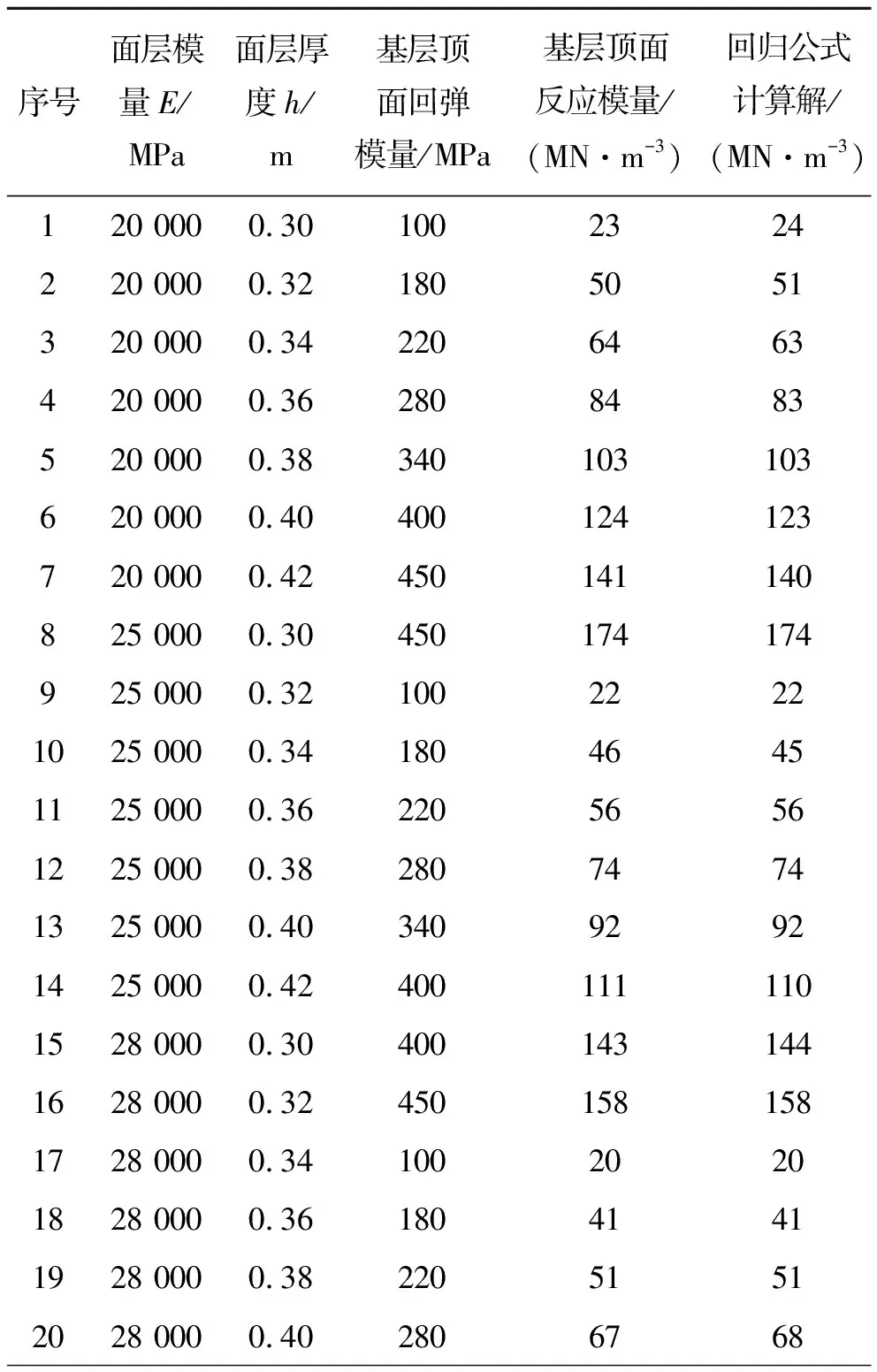
表6 正交试验方案及结果

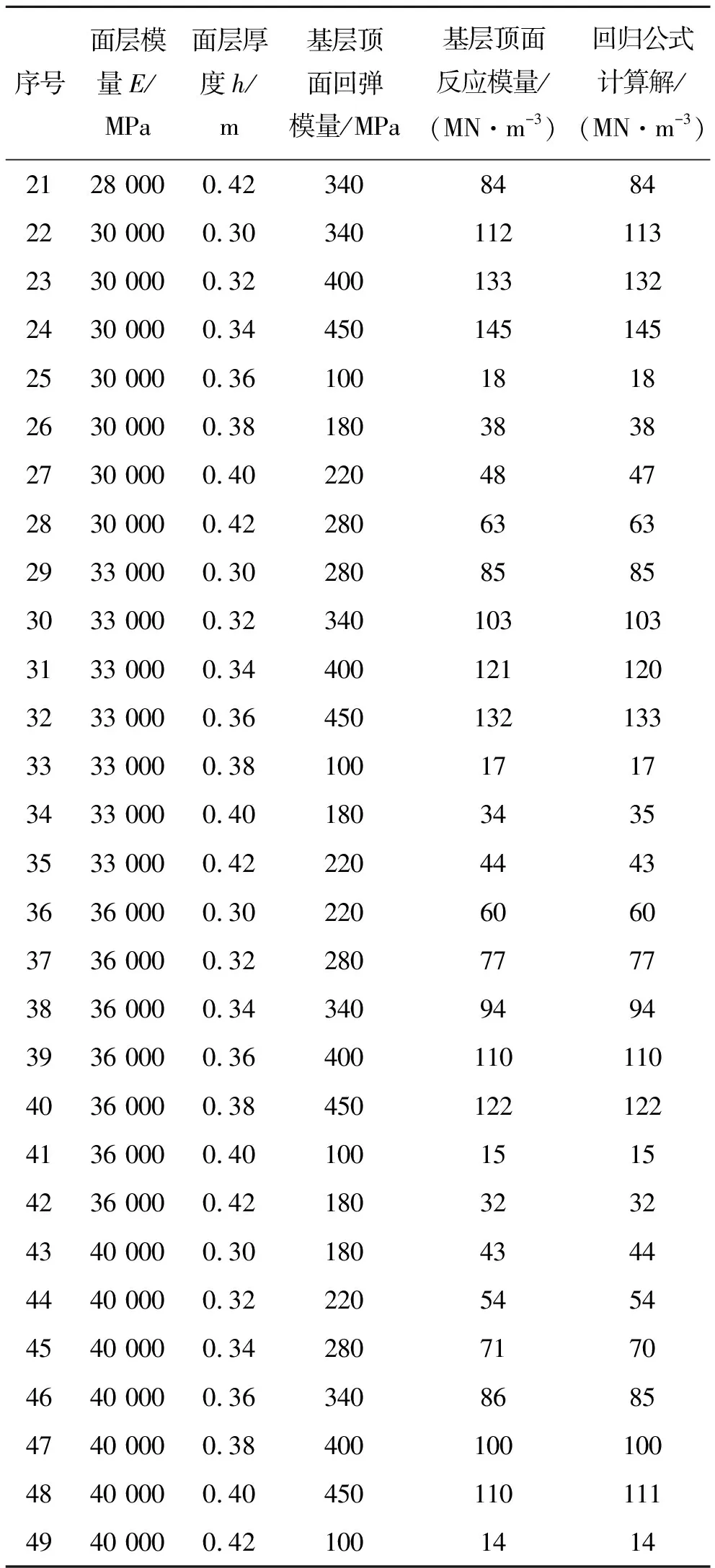
续表6

极差分析可以确定各因素对试验指标的影响及最佳方案，该文极差计算结果见表7。由表7可知：基层顶面回弹模量对反应模量的影响最显著，而其他各因素均有不同程度的影响。按极差值大小排序依次是：基层顶面回弹模量>面层厚度>面层模量。

综合上述关系，建立地基模量转换关系模型如式(7)：

K=[ah+blnE+c]E0dh2+eh+f

(7)

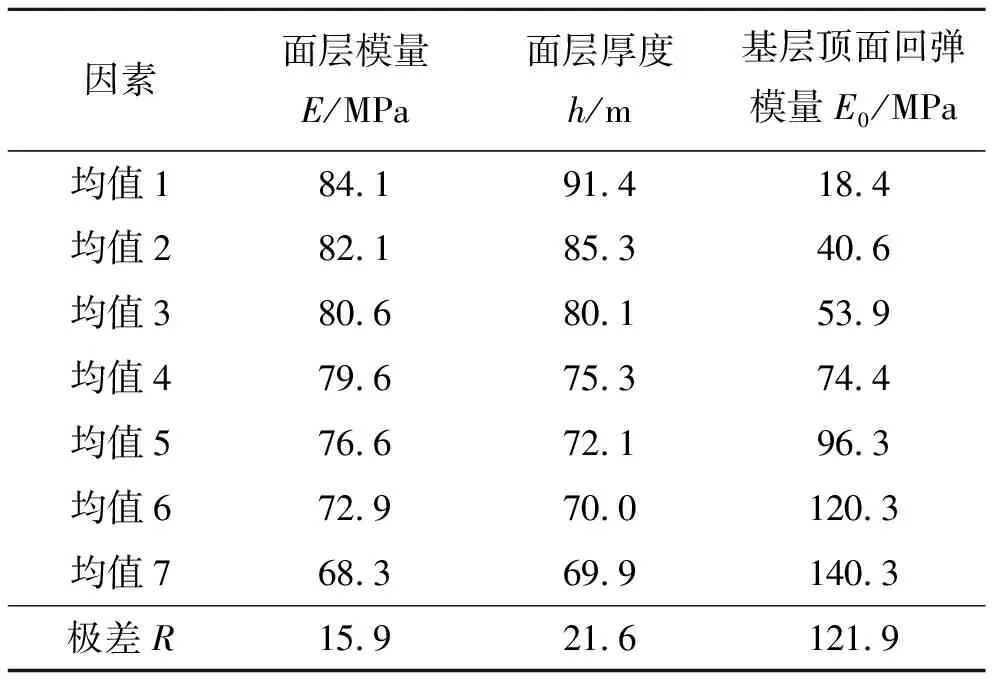
表7 极差分析结果

借助Matlab软件编写程序，展开多元非线性拟合，即可确定a、b、c等参数，见表8。

表8 拟合参数

则基顶反应模量与基顶回弹模量的转换关系模型如式(8)所示：

K=[-0.112h-0.013lnE+0.212]·

E01.629h2-1.123h+1.536

(8)

4 实例验证

以北京沙河机场为例，水泥混凝土道面，混凝土弹性模量为35 000 MPa，泊松比为0.15，厚度为0.18 m，地基泊松比为0.35。在刚硬圆盘上加载，圆盘半径为20 cm，识别出的地基参数见表9[9]，由转换关系模型式(8)计算出的地基反应模量K′ 及误差如表9所示，可以看出误差均在8%以内，说明转换模型具有较高的精度。

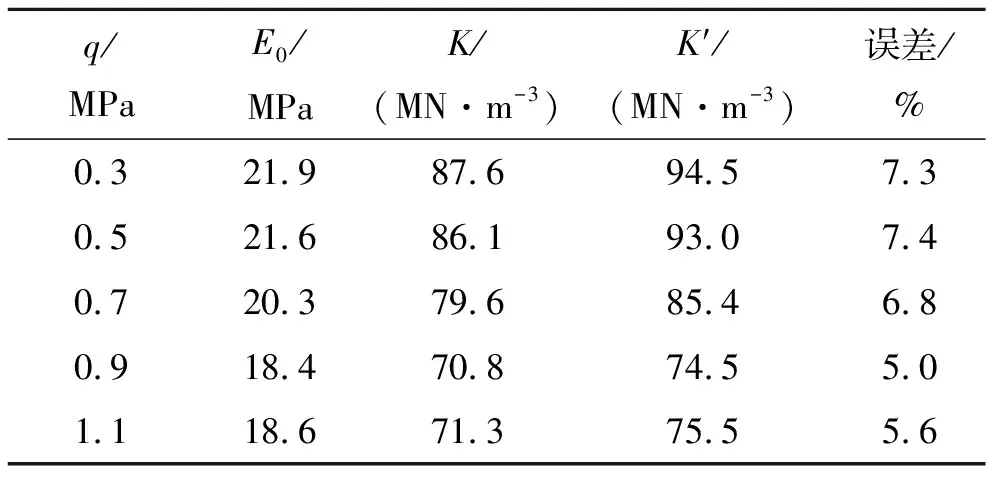
表9 模型精度验证误差

5 结论

通过有限元模拟及49组数据正交计算，对基顶回弹模量与反应模量的转换关系进行研究，解决了目前机场刚性道面设计中，基顶反应模量需由经验获得的弊端，得出以下结论：

(1) 基层顶面反应模量与回弹模量呈幂指数函数的变化规律。

(2) 回弹模量固定不变时，面层厚度增大，面层厚度固定不变时，弹性模量增大，转换求得的地基反应模量均减小。当面层厚度由0.31 m增大至0.43 m，转换所得的地基反应模量减幅均在30%左右；机场刚性道面的道面层弹性模量对转换关系的影响与厚度相比较小，当面层弹性模量由21 000 MPa增大至41 000 MPa时，转换所得的地基反应模量减幅均在20%左右。

(3) 开展极差分析，确定了单因素影响规律，建立了基顶回弹模量与反应模量的转换公式。以北京沙河机场数据为例，对模型的精度进行验证，结果显示，转换误差均控制在8%以内，说明模型具有较高精度。