融合动态邻域搜索机制的蚁群系统算法*

郭文强 杜正毅

融合动态邻域搜索机制的蚁群系统算法*

郭文强 杜正毅

（新疆财经大学信息管理学院，新疆 乌鲁木齐 830012）

针对蚁群算法收敛速度慢，容易陷入局部最优解等问题，提出一种融合动态邻域搜索机制的蚁群系统（DNS-ACS）算法。首先，在蚁群系统算法的基础上，引入2-opt算子进行局部搜索，加快算法收敛速度；然后，动态调整邻域搜索范围和信息素更新规则，使其跳出局部最优，避免早熟现象；最后，利用本文提出的DNS-ACS算法对16个经典TSP算例进行仿真模拟，并与其他算法进行对比实验。实验结果表明，DNS-ACS算法的求解精度明显提高，证明了该算法的有效性。

蚁群算法；旅行商问题；动态邻域搜索；信息素更新

0 引言

旅行商问题（travelling salesman problem, TSP）是指给定一系列城市和每两座城市之间的距离，求解访问每座城市一次并回到起始城市的最短回路，是一类标准的组合离散优化问题[1]，也是一个NP难问题。

TSP有精确算法和启发式算法2种求解方法。其中，精确算法包括切割平面法、动态规划法、分支定界法[2]等，该类方法可有效求得TSP的最优解，但需要指数时间，不适用于大规模的TSP；启发式方法包括蚁群优化算法（ant colony optimization, ACO）[3]、帝国竞争算法[4]、模拟退火法[5]、猫群算法[6]、禁忌搜索算法[7]、粒子群优化算法[8]、人工蜂群算法[9]等，该类算法能够在有限的时间内得到问题的满意解，是解决TSP的常用方法。

蚁群算法是具有代表性的群智能算法之一[10]，由DORIGO Marco于1992年提出，并将其应用于解决TSP，取得较好效果。之后，各国学者不断优化该算法[11-15]，出现了最大最小蚁群（max min ant colony system, MMAS）算法[16]，蚁群系统（ant colony system, ACS）算法[17]等，这些算法优化了信息素更新规则，一定程度地解决了蚁群算法中信息素积累速度过快，搜索空间不足的问题，但仍然容易陷入局部最优。

为此，本文提出融合动态邻域搜索机制的蚁群系统（dynamic neighborhood search ant colony system, DNS-ACS）算法。首先，利用2-opt算子改进当前阶段的解；然后，搜索当前最优解各个节点周围邻域并记录邻域内的路径，在信息素更新阶段将信息素按照一定规则分配到记录的路径中；最后，动态调整信息素释放量以及邻域搜索范围，使算法在前期实现快速收敛，在后期有效跳出局部最优解。

1 蚁群算法

蚁群算法的灵感来源于蚂蚁觅食方式。蚂蚁在寻找食物时，在路径上遗留一种叫做信息素的化学物质。由于目标距离及挥发因素的影响，蚁群和最近食物之间的路径存在更多的信息素，从而吸引更多的蚂蚁跟随相同的路径。一旦食物耗尽，蚂蚁就会放弃这条路径，伴随着信息素的挥发，迫使蚂蚁重新开始随机寻找另一种食物。

蚁群算法随机初始化所有蚂蚁，每个蚂蚁搜索一个潜在的解决方案。在迭代过程中，蚁群算法为求解路径的每条边分配信息素，蚂蚁根据信息素的浓度，移动到尚未访问的节点，构建一个可行的解决方案。在蚁群算法中，蚂蚁根据公式(1)访问下一个节点。

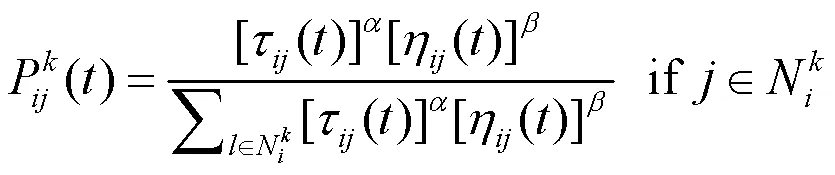
式中：

在蚁群系统算法中，蚂蚁访问节点的方式有所改变，访问规则如公式(2)所示。

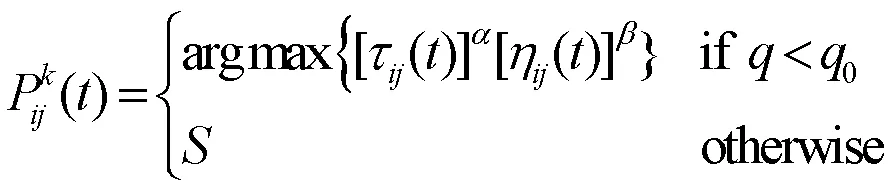
式中：

的访问方式按公式(1)进行。

蚁群系统算法中，蚂蚁访问下一个节点时，利用公式(3)局部更新路径信息素，这个过程称为局部信息素更新。

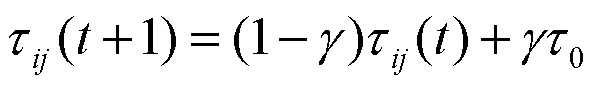
式中：

在所有蚂蚁访问结束后，利用公式(4)更新路径信息素，这个过程称为全局信息素更新。

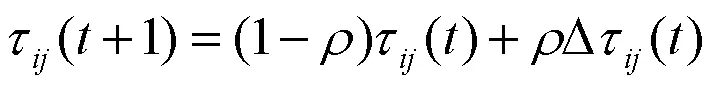
式中：

式中：

由于算法在搜索阶段开始时，各条路径的信息素分布均匀，因此在蚁群算法和蚁群系统算法中，前期具有一定的盲目性，导致收敛速度较慢；而后期，算法在路径上积累了大量的信息素，降低了搜索其他路径的机会。本文在蚁群系统算法的基础上，提出的DNS-ACS算法在一定程度上解决了这些问题。

2 DNS-ACS算法

本文提出的DNS-ACS算法主要进行如下改进：

1）引入2-opt算子，避免路径交叉带来的距离损耗，实现算法快速收敛；

2）融合邻域搜索机制，通过搜索邻域节点，扩大搜索范围，避免算法陷入局部最优；

3）动态调整邻域搜索及信息素更新规则，为寻找最优路径提供合理导向。

2.1 2-opt算子

2-opt算法是局部搜索算法，通过对局部解进行优化，帮助蚁群算法避免局部极小值。本文引入2-opt算子求解TSP[18]，通过将当前解所表示的路径中已有的两条边置换，产生一条新路径，若新路径更短，则保留；重复这个过程，直到没有发现更短的路径为止。2-opt算子的优化过程如图1所示。

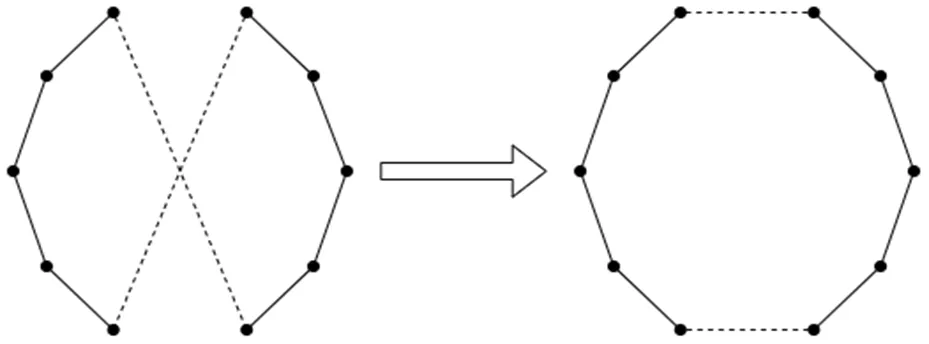
图1 2-opt算子优化过程示意图

由图1可以看出，2-opt算子能够将虚线部分的路径优化，使优化后的路径更短，有效提升问题解的质量。

2.2 邻域搜索机制

蚂蚁在寻找下一个目标节点时，符合最优解的目标往往在蚂蚁周围的相邻节点产生。因此，在DNS-ACS算法中，蚂蚁经过每个节点时，标记周围距离最近的相邻节点，并记录当前节点与标记点之间的路径，标记个数为。蚂蚁在经过某个节点时，建立邻域，寻找标记点及与当前节点路径的过程如图2所示。

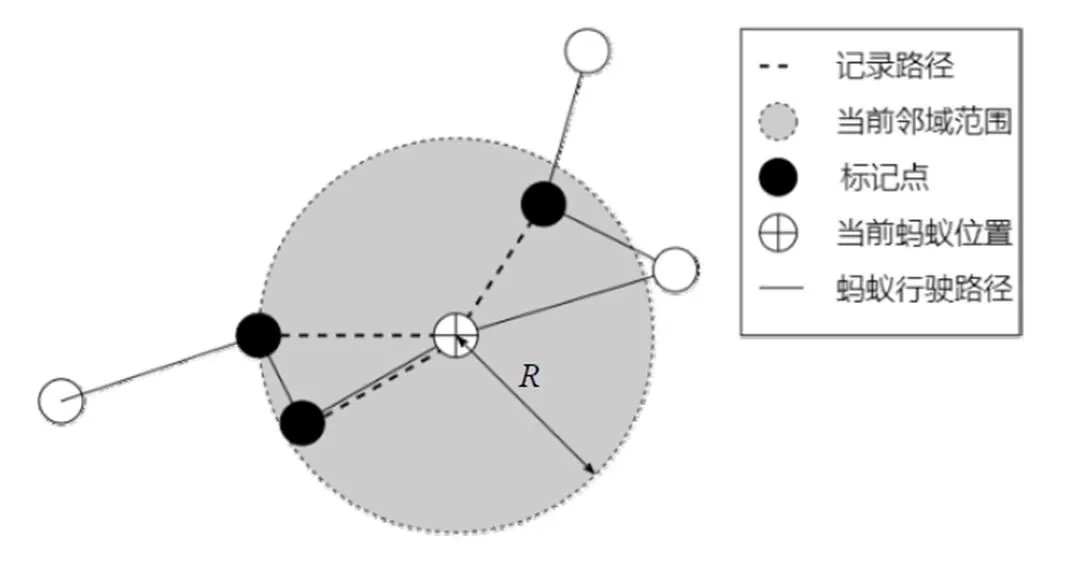
图2 邻域搜索机制示意图

由图2可以看出，蚂蚁经过每个节点时，会建立以该节点为中心，半径为的邻域范围。的计算公式为

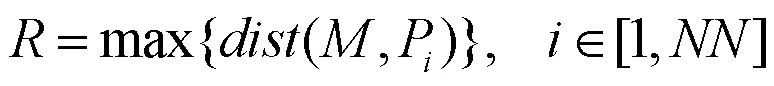
式中：

——当前节点；

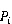
2.3 信息素动态更新

在蚁群算法中，每只蚂蚁经过路径时都释放信息素，导致信息素积累速度过快。随着迭代次数不断增加，蚂蚁容易集中在同一条路径，导致收敛过快，结果误差偏大。蚁群系统算法通过局部信息素更新和全局信息素更新，避免了路径间信息素差异过大。但由于信息素更新方式是静态的，仍难以跳出局部最优解。

本文通过动态调整邻域的信息素，使其在加快算法收敛速度的同时扩大搜索范围，避免早熟现象。该过程分为2个步骤。

1）对现有的最优路径(,)按公式(7)进行信息素补偿，以加快算法收敛速度。

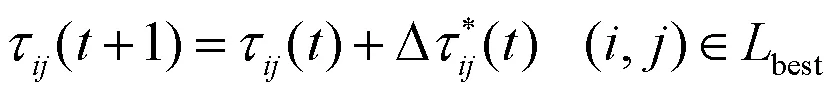
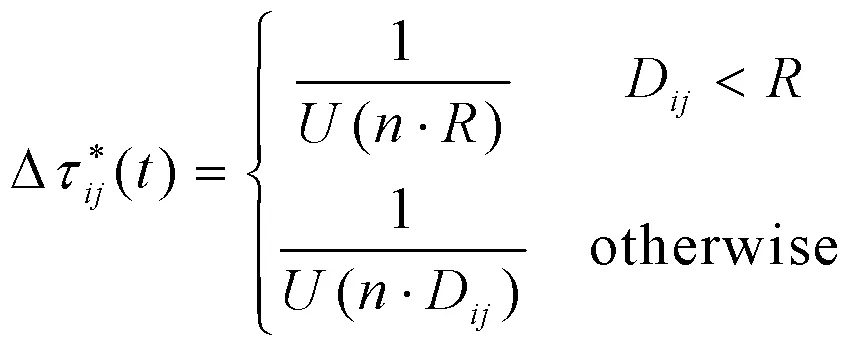
式中：

即若节点处于其当前邻域范围内，则信息素的补充值为一个与领域范围半径相关的固定值；若节点处于当前邻域范围外，则信息素的补充值随两点距离的增大而减小。

2）为平衡可能存在的更优解路径与现有最优路径之间的信息素差距，向当前最优路径节点邻域内的其他节点释放信息素，增加蚂蚁前往这些节点的概率，扩大搜索范围。

首先，利用公式(9)对某一节点记录的各条路径间的距离进行标准化处理；

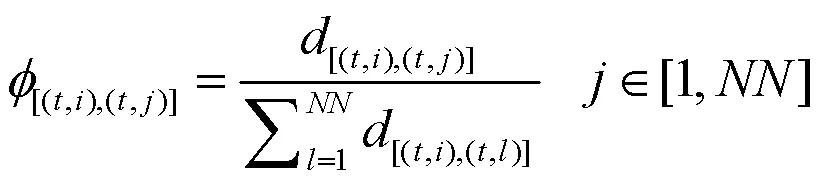
然后，利用公式(10)对记录的路径进行信息素更新。

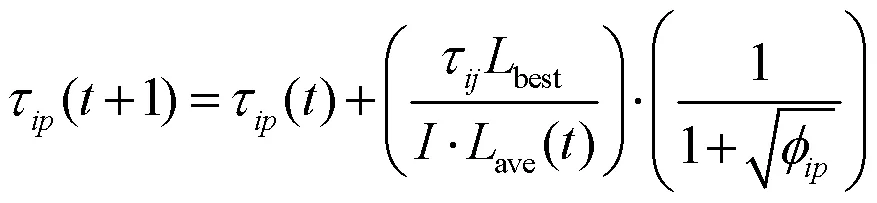
式中：

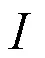
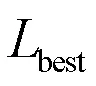
2.4 动态邻域搜索机制

在邻域搜索时，若每次迭代的结果较上一次有所提升，则表明算法在当前环境下能够找到更优解的可能性较大，应适当缩小搜索范围，集中搜索可能出现的更优解；若长时间最优解没有更新，则表明算法陷入停滞，应扩大搜索范围，增加解的多样性，在更远的邻域内使现有解得到更新。本文对标记数按公式(11)进行调整。

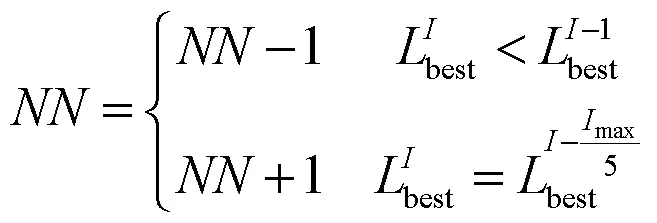
式中：

为避免邻域范围过大或过小，干扰蚂蚁寻优过程，设定一个阈值，如公式(12)所示。

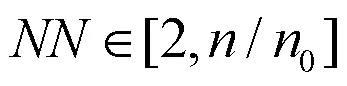
式中：

2.5 算法流程

DNS-ACS算法流程图如图3所示。

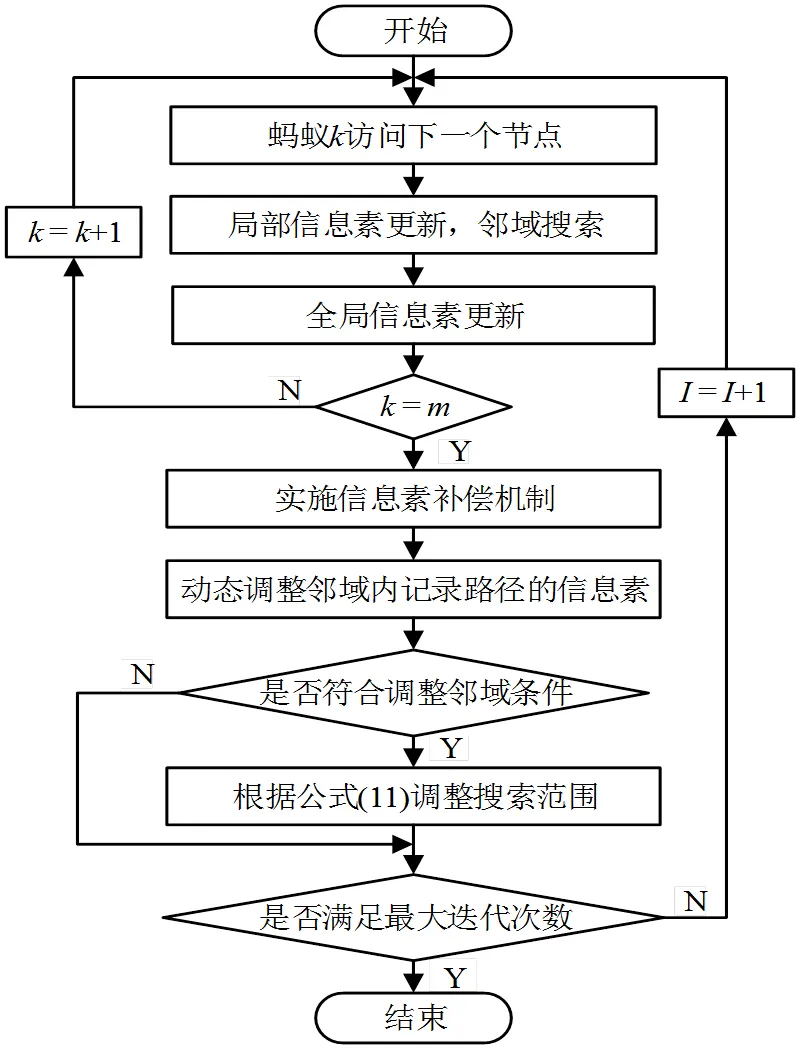
图3 算法流程图

3 实验仿真

3.1 参数设置

本实验采用TSPLIB数据库中的TSP数据集，测试算法性能。首先，在数据集中选取16个算例，比较ACS、ACS+2-opt、本文DNS-ACS算法；其次，利用8个数据集比较本文DNS-ACS算法与5种文献[5,19-22]算法性能。参数设置如表1所示。

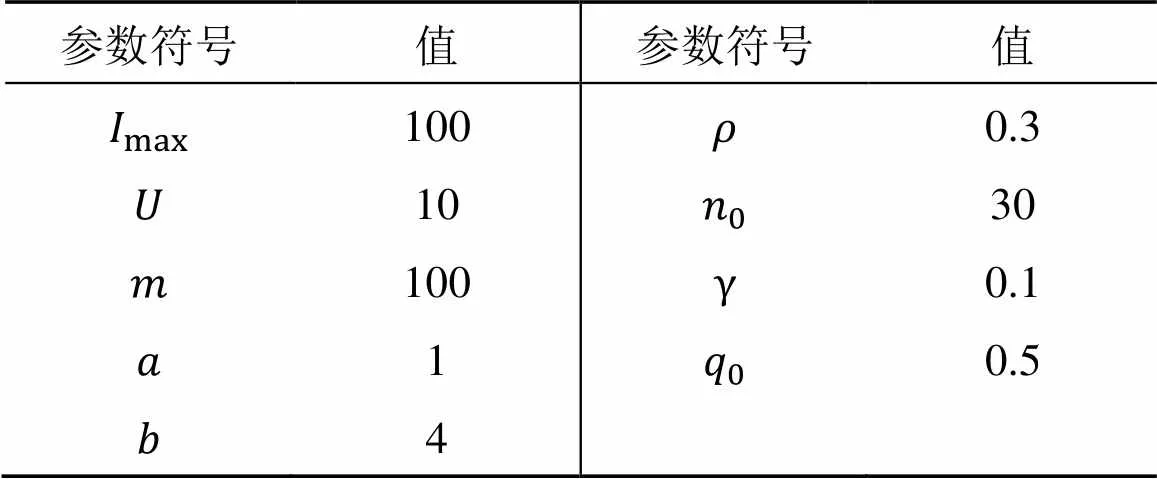
表1 参数设置

通过Matlab 2018b实现DNS-ACS算法，并分别运行TSP数据集的16个算例，比较其平均解，误差率（）以及每次运行的最优解。

3.2 与传统算法比较

为验证DNS-ACS算法能有效优化TSP，本文利用ACS、ACS+2-opt、DNS-ACS三种算法分别对TSP算例库中的16个算例进行实验。为保证参数的一致性，三种算法的参数都按表1设置。每种算法在每个算例中运行10次，取最优解平均值，并利用公式(13)计算误差率，结果如表2所示。

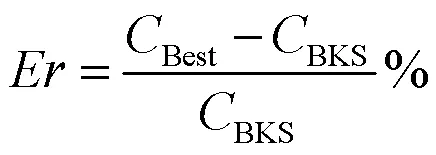
式中：

——误差率；

由表2可知：ACS算法仅找到oliver30算例的最优解，其他算例都有不同程度的误差，其中lin318算例的误差率达到7.93%；ACS+2-opt算法找到9个算例的最优解，其中误差率高于0.5%的算例有3个；DNS-ACS算法找到12个算例的最优解，其他算例的误差率在0.5%以内，寻优能力明显优于另外2种算法。此外，DNS-ACS算法在每个算例中的最优值，都是3种算法中最小的，证明了该算法的优化是有效的。

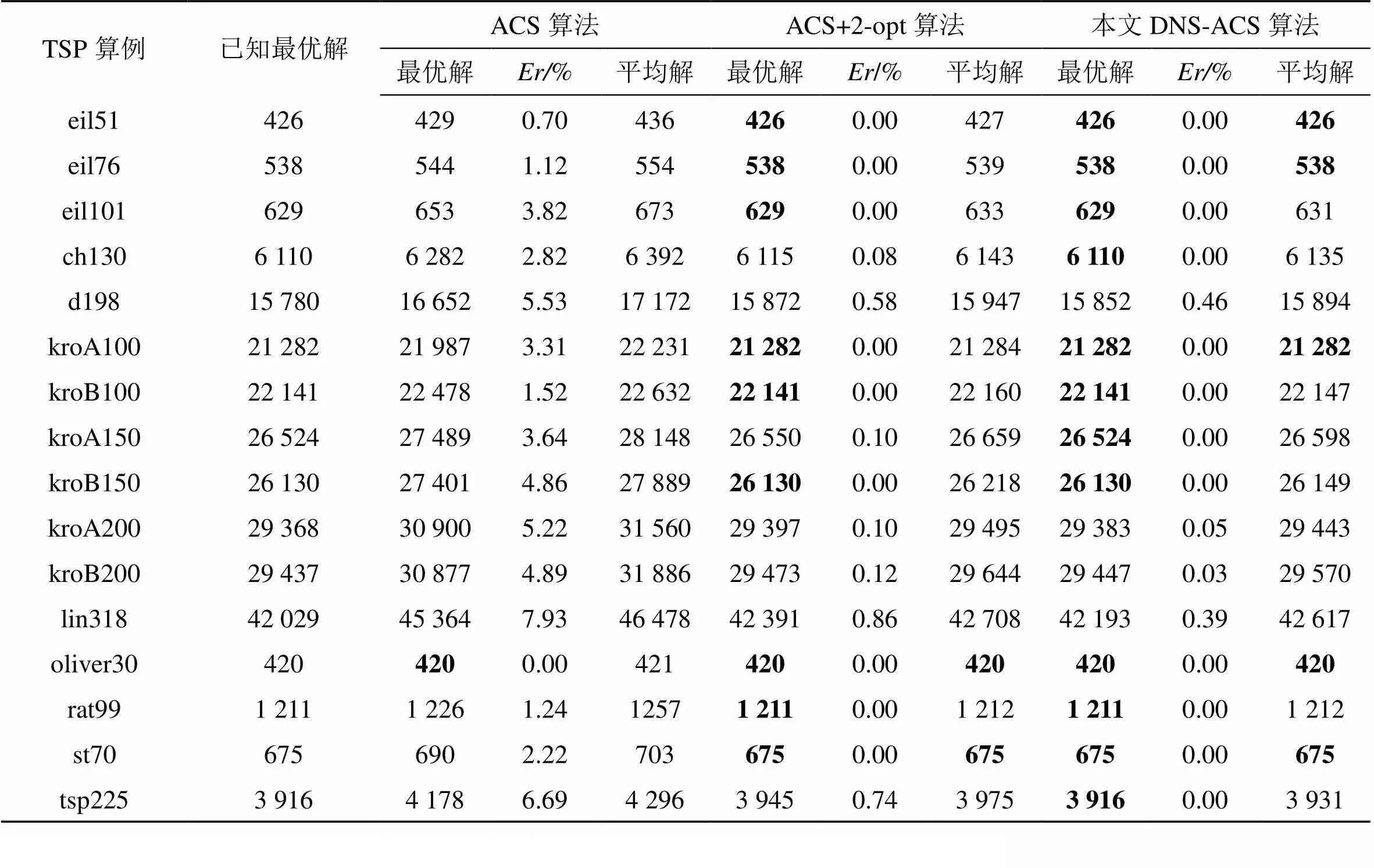
表2 DNS-ACS算法与ACS算法、ACS+2-opt算法对比结果

注：最优解和平均解的结果四舍五入取整，标黑表示达到已知最优解。

本文选择6个规模较大的算例，通过图像的形式对ACS、ACS+2-opt、DNS-ACS三种算法的收敛曲线进行对比，如图4所示。

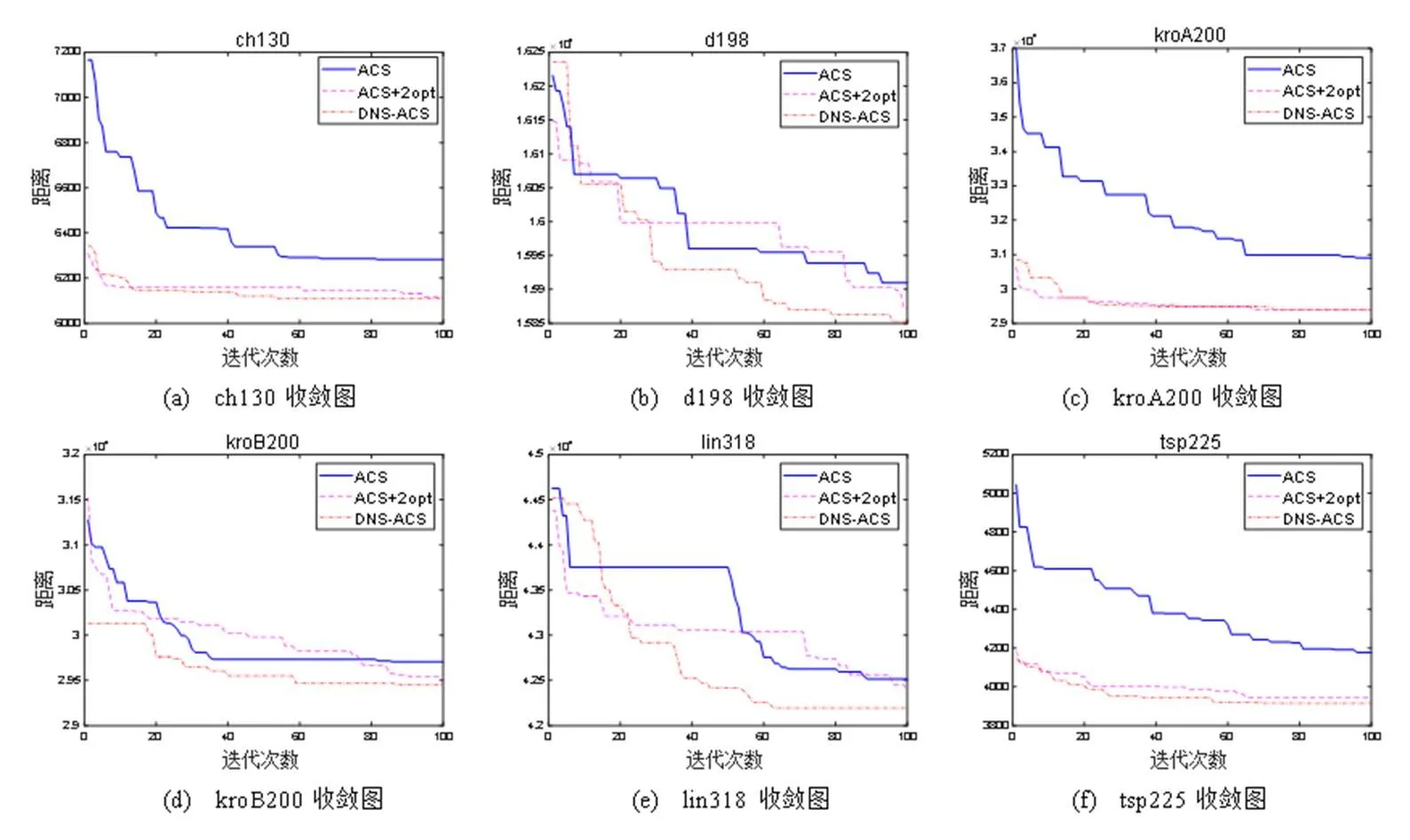
图4 ACS、ACS+2-opt、DNS-ACS三种算法的收敛曲线对比图

由图4可知，DNS-ACS算法的收敛速度较快，求解精度最好，表明该算法对求解TSP问题有明显效果。

为对仿真结果进行进一步验证，采用DNS-ACS算法求解的最优路径如图5所示。

图 5 仿真实验结果

由图5可以看出：采用DNS-ACS算法求解的最优路径是一个闭环，其间没有形成交叉点。

3.3 与其他文献算法比较

为进一步证明DNS-ACS算法的有效性，本文选取文献[5,19-22]的算法在这8个算例中进行比对实验，结果如表3所示。

表3 DNS-ACS算法与其他文献算法比对结果

注：最优解和平均解的结果四舍五入取整，“—”表示在文献中没有相应数据，标黑表示算法中的最优解。

由表3可以看出：在这8个算例中，DNS-ACS算法解的精度较其他算法有明显提高，从而验证该算法具有较好的优化性能。

4 结语

针对蚁群算法的不足，本文融入动态邻域搜索机制，结合2-opt算子，并通过改进信息素更新机制，在加快算法收敛速度的同时，扩大搜索范围，从而使算法更好地跳出局部最优解，实现算法优化。通过对TSPLIB数据库中的16个算例的比对，证明该算法的有效性。但是对于较大规模的算例，所求得解的精度仍有上升的空间。日后的研究中，将针对这一问题继续完善对算法的优化。

[1] DANTZIG G B, FULKERSON D R, JOHNSON S M. On a linear-programming, combinatorial approach to the traveling-salesman problem[J]. Operations Research, 1959,7(1):58-66.

[2] GOUVEIA L, LEITNER M, RUTHMAIR M. Extended formulations and branch-and-cut algorithms for the black-and-white traveling salesman problem[J]. European Journal of Operational Research, 2017:908-928.

[3] WEI Gao. New ant colony optimization algorithm for the traveling salesman problem[J]. International Journal of Compu-tational Intelligence Systems,2020,13(1): 44-55.

[4] ARDALAN Z, KARIMI S, POURSABZI O, et al. A novel imperialist competitive algorithm for generalized traveling sales- man problems[J]. Applied Soft Computing, 2015,26:546- 555.

[5] 陈科胜,鲜思东,郭鹏.求解旅行商问题的自适应升温模拟退火算法[J].控制理论与应用,2021,38(2):245-254.

[6] 杨进,郑允,马良.改进的猫群算法求解TSP[J].计算机应用研究,2017,34(12):3607-3610.

[7] EZUGWU E S, ADEWUMI A O, FRNCU M E. Simulated annealing based symbiotic organisms search optimization algorithm for traveling salesman problem[J]. Expert Systems with Applications, 2017,77:189-210.

[8] 杨云亭,王鹏.求解旅行商问题的多尺度量子自由粒子优化算法[J].计算机应用,2020,40(5):1278-1283.

[9] CHOONG S S, WONG L P, LIM C P. An artificial bee colony algorithm with a Modified Choice Function for the traveling salesman problem [C]// IEEE International Conference on Sys-tem, Man, and Cybernetics (SMC) 2017. IEEE, 2017.

[10] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[J]. IEEE tran-sactions on systems, man and cybernetics. Part B, 1996,26(1): 29-41.

[11] ZHANG Zhaojun, XU Zhaoxiong, LUAN Shengyang, et al. Opposition-based ant colony optimization algorithm for the traveling salesman problem[J]. Mathematics, 2020,8(10):1650.

[12] EBADINEZHAD S. DEACO: adopting dynamic evaporation strategy to enhance ACO algorithm for the traveling salesman problem[J]. Engineering Applications of Artificial Intelligence, 2020,92:103649.

[13] FADL D, KHALIL EL H, HASSAN M, et al. Dynamic flying ant colony optimization (DFACO) for solving the traveling salesman problem[J]. Sensors (Basel, Switzerland),2019,19(8): 1837.

[14] JIANG C, WAN Z, PENG Z. A new efficient hybrid algorithm for large scale multiple traveling salesman problems[J]. Expert Systems with Applications, 2019,139:112867.

[15] 张立毅,肖超,费腾.基于细菌觅食的改进蚁群算法[J].计算机工程与科学,2018,40(10):1882-1889.

[16] STUTZLE T, HOOS H H. MAX-MIN ant system[J]. Future Generation Computer Systems, 2000, 16(8): 889-914.

[17] DORIGO M, GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997,1(1):53-66.

[18] 李俊,童钊,王政.一种并行ACS-2-opt算法处理TSP问题的方法[J].计算机科学,2018,45(S2):138-142.

[19] 陈思远,林丕源,黄沛杰.指针网络改进遗传算法求解旅行商问题[J].计算机工程与应用,2020,56(19):231-236.

[20] 乔东平,裴杰,李浩,等.改进蚁群算法求解TSP问题研究[J].机械设计与制造,2019(10):144-149.

[21] 陈颖杰,高茂庭.基于信息素初始分配和动态更新的蚁群算法[J].计算机工程与应用,2022,58(2):95-101.

[22] 孟静雯,游晓明,刘升.结合协同机制与动态调控策略的双蚁群算法[J].计算机科学与探索,2021,15(11):2206-2221.

Ant Colony System Algorithm Combining Dynamic Neighborhood Search Mechanism

GUO Wenqiang DU Zhengyi

(School of Information Management Xinjiang University of Finance and Economics, Urumqi 830012, China)

Aiming at the problems of slow convergence speed and easy to fall into local optimal solution of ant colony algorithm, an ant colony system (DNS-ACS) algorithm combining dynamic neighborhood search mechanism is proposed. Firstly, based on the ant colony system algorithm, the 2-opt operator is introduced for local search to speed up the convergence speed of the algorithm; Then, dynamically adjust the neighborhood search range and pheromone update rules to make it jump out of the local optimum and avoid premature phenomenon; Finally, the DNS-ACS algorithm proposed in this paper is used to simulate 16 classical TSP examples, and compared with other algorithms. Experimental results show that the accuracy of DNS-ACS algorithm is significantly improved, which proves the effectiveness of the algorithm.

ant colony algorithm; traveling salesman problem; dynamic neighbors search; pheromone update

TP301.6

A

1674-2605(2022)02-0003-08

10.3969/j.issn.1674-2605.2022.02.003

郭文强，男，1975年生，博士，教授，博士生导师，主要研究方向：人工智能、信息安全。E-mail: gwq@xjufe.edu.cn

杜正毅，男，1996年生，硕士研究生，主要研究方向：智能算法。E-mail:1247397930@qq.com

基金项目：国家自然科学基金项目（61941205）；天山雪松项目（2020XS07）。

郭文强,杜正毅.融合动态邻域搜索机制的蚁群系统算法[J].自动化与信息工程,2022,43(2):15-22.

GUO Wenqiang, DU Zhengyi. Ant colony system algorithm combining dynamic neighborhood search mechanism[J]. Automation & Information Engineering, 2022,43(2):15-22.