基于信息熵的预制混凝土构件生产系统状态度量
2022-05-13阮敏浩
阮敏浩, 徐 峰
(上海交通大学 a. 船舶海洋与建筑工程学院; b. 上海市公共建筑和基础设施数字化运维重点实验室, 上海 200240)
生产扰动普遍存在于预制混凝土构件生产中,分为显性扰动和隐形扰动[1]。前者囊括紧急订单、交货期变化、预制构件数量变化、设计变更和设备损坏等发生后能被立即识别的偶然性事件,而后者伴随生产实时发生但不能被立即识别,需要通过时间积累才能显现影响,诸如设备使用率下降和工人加工时间波动等。上述生产扰动都是预制混凝土构件生产系统运行过程中的不确定因素,会导致实际生产偏离调度方案,且从整体来看偏离程度与时间推移正相关[2]。当偏离达到一定程度就需要对预制混凝土构件生产进行再调度,再调度过迟会导致在超过某个时刻后实际生产状况与调度方案预期完全不符,从而使调度方案完全失效;反之,过早的再调度会致使调度相关成本大幅增加。因此,合理的预制混凝土构件生产再调度时刻的确定成为关键。
准确识别生产扰动是进行生产再调度的基本前提[3],生产再调度的本质就是对于复杂生产系统的状态进行评估。现有文献对于预制构件生产再调度的研究大多聚焦于显性扰动,如Kim等[4]针对交付日期不确定的动态调度模型,Wang等[5]考虑紧急订单下的动态调度模型,其再调度时刻都是明确的,且再调度的结果仅针对当前,无法为后续生产提供再调度指导。蒋静静[6]建立了隐性扰动下人工调整策略模拟模型,该模型虽考虑了隐性扰动,但再调度时刻的判断基于调度预期与实际加工之间的时间差值与主观设立阈值的比较,缺乏理论支撑,且无法为提高调度有效性提供方向。基于热力学中熵概念的信息熵,描述的是信息源的不确定程度[7],与生产系统、运行过程中的不确定性契合[8]。近年来,信息熵理论应用于制造系统复杂性测度取得较大进展,其在调度中的应用也被不断挖掘。饶运清等[9]应用信息熵理论研究制造系统的复杂性测度问题。在此基础上,何非[10]利用系统复杂度偏离度描述实际情况与原调度方案的符合程度。张剑亭等[11]提出了基于信息熵的梯级水库联合优化调度增益分配法。黄英杰等[12]借鉴信息熵理论设计出在车间调度问题求解当中较为适用的熵增强的混沌粒子群算法。Ashkan等[13]将影响混流装配系统复杂性的因素的信息熵进行叠加,得到混流装配系统复杂性的度量方法。张志峰等[14]构建了单元化制造系统的结构熵与运行熵函数,并根据调度理论建立了系统状态评估指标。薄洪光等[15]针对机床装配线生产特征,分别建立了三阈值与单阈值扰动识别法。
综上所述,隐性扰动在生产过程中客观存在且其程度难以主观衡量,为了保障调度方案执行的有效性,再调度必不可少。因此考虑隐性扰动的预制混凝土构件生产系统再调度时刻的确定,成为当前亟需解决的焦点问题。近年来,信息熵理论在制造业生产系统中进行了丰富的实践应用。但熵函数的搭建依赖于对具体系统的信息描述,当前已有研究成果适用范围有限,无法直接应用于预制混凝土构件生产系统。因此,本文以预制混凝土构件生产系统为研究对象,为实现对其状态的信息描述分别构建结构熵与运行熵函数,提出最大可行调度时限与调度符合度两项指标,对预制混凝土构件生产调度状态进行定量评估,并据此制定预制混凝土构件生产系统合理的再调度时刻,以及生产系统运行的优化对策。
1 预制混凝土构件生产系统的状态熵函数
信息熵的概念最早由Shannon等[16]提出。如果X表示一个系统,xi,pi(i=1,2,…,n)分别为该系统n个可能出现的状态及各状态发生的概率,则系统X的信息熵E(X)可定义为:
(1)
E(X)衡量了描述系统X所需的信息量,信息熵越大,反映系统的不确定性越大。
1.1 预制混凝土构件生产系统特点
设计标准化与管理信息化使预制混凝土构件生产效率提高且成本下降,大幅节省了人力资源,加快了施工进度,受到国家大力推广。合理的生产调度、再调度以及预制混凝土构件生产系统管理,对于装配式建筑充分发挥其优势有着至关重要的作用。
对于批量化的预制混凝土构件流水线生产而言,其生产系统与单元化制造车间或简单的机械产品装配车间截然不同。预制混凝土构件生产囊括混凝土浇筑、固化养护、构件运输等不同性质的工序,并涉及模具、钢筋、混凝土以及工人工作时间等多项约束,且其调度方案中存在着同一时刻多构件多工序同时进行的场景,因此无法直接套用一般制造系统复杂度模型[17~20]解决预制混凝土构件生产系统状态度量的问题。
1.2 预制混凝土构件生产系统的结构熵
预制混凝土构件生产系统的结构熵是描述系统在静止状态下每一个生产资源或构件预期拥有的状态所需要的信息量Cs(也称为静态复杂度)。预制混凝土构件生产系统的静态复杂度涵盖生产所需的资源构成、预制构件的品种和数量、工艺路线等,因此又称为结构复杂性。对于某个特定的预制混凝土构件生产系统,其涉及的可预期状态取决于相应的生产调度方案,因此可根据生产调度方案中所包含的信息量对其静态复杂性进行测度。
假设某条预制混凝土构件生产流水线为一个生产系统,将生产M(M≥1)个预制构件,第i个预制构件预期拥有的状态数为Si。根据式(1),第i个预制构件的结构熵Csri可由式(2)计算。
(2)
式中:pij为预制构件i处于状态j的概率,1≤j≤Si。
根据信息熵的性质,可进一步得到整条生产线上M个预制构件的结构熵Css为:
(3)
预制混凝土构件生产系统结构熵的计算前提是对系统内的状态进行认定,而状态的认定及状态数取决于研究粒度,研究粒度的选择需要综合考虑生产系统控制的侧重点及实际可操作性。例如,若生产经营者侧重于生产设备的负荷问题,则生产设备的可能状态可取“构件生产”“设备空闲”等粗粒度事件;若侧重于预制构件的具体生产情况,则可进一步将状态定义为“构件A混凝土浇筑”“构件B固化养护”等粒度更细的事件。
1.3 考虑隐性扰动的预制混凝土构件生产系统运行熵
上述结构熵计算仅需考虑依照调度方案开展生产所预期发生的状态,而生产系统运行过程中实际发生的状态则由动态复杂性来描述,因此又称运行复杂性。此处,将预制混凝土构件生产系统的运行熵定义为描述系统在生产运行过程中各生产资源或构件的实际状态所需要的信息量Cd(也称为动态复杂度)。这里所说的实际状态可按照是否如调度方案所期望分为两大类:一类是符合调度方案预期的受控状态;另一类是由于生产扰动(尤其是囊括了隐性扰动)而偏离调度方案预期的失控状态,如工序操作超时、设备故障等。
记该预制混凝土构件生产系统中所有预制构件的受控状态概率为P,预制构件i的失控状态数记为Ni,则整个生产系统的运行熵为Cds:
(4)
式中:p′ij为预制构件i处于失控状态j的概率。上式中第二项为预制混凝土构件生产系统运行过程中由于偏离调度方案而产生的熵值,记为Cdd,它反映了预制混凝土构件生产系统在运行过程中的不确定性程度,也能反映出隐性扰动对于系统运行的影响大小:
(5)
2 预制混凝土构件生产系统状态的评估
传统预制混凝土构件生产调度研究更多着眼于对初始调度方案的优化,其优化目标一般为最小完工时间、最高设备利用率或最低的交付罚款等[21~26]。随着制造业信息化水平提升,预制构件生产信息监控系统逐步完善[27]。但由于缺乏科学定量的评价方法,调度方案的实际执行情况鲜有被研究关注,即生产调度有效性的研究被忽视了。生产调度有效性是指预制混凝土构件生产调度方案的实际执行情况与预期结果的符合程度。调度有效性越好,则调度方案对于实际生产的指导性越强;反之,无论事先对生产调度方案开展怎样的优化,如果执行后的情况和预期完全不符,再精妙的生产调度也毫无意义。生产扰动(尤其是隐性扰动)的不可避免,注定了预制混凝土构件生产调度的预期和实际执行之间必然存在偏差,而生产过程中为了纠偏,必然需要进行再调度。过早过频繁或过迟的再调度都会为生产带来负面影响。因此,本文从生产再调度与系统运行优化需求两个角度提出最大可行调度时限和调度符合度两项量化指标,对预制混凝土构件生产系统状态进行评估。
2.1 评估调度时限合理性
调度时限又称调度周期,即调度方案覆盖的时长。传统生产调度操作中,调度时限往往是根据构件种类或订单大小预先设定,如一天、一周等。如此粗略设定的调度时限很难契合生产系统实际运行过程中发生的偏离,从而很难做到合理及时地纠偏。以信息论和制造系统复杂度的观点来看,生产调度方案在实际运行过程中发生偏离的本质,就是初始调度方案中包含的部分静态信息量转化成生产系统运行过程中的动态信息量。由此可见,只要能够测定出生产系统结构熵向运行熵的转化率,就可以据此评估调度时限的合理性。
调度方案中的结构熵可根据式(2)进行计算,其值为预制混凝土构件生产系统在某一时刻的结构熵。对于调度时限为T、且对生产系统实际运行状态进行动态观测的时间间隔(即调度精度)为Δt的调度方案,其结构熵C′ss为:
(6)
如前所述,预制混凝土构件生产系统在实际运行过程中某一时刻由于偏离调度预期而产生的熵值为Cdd,则生产系统偏离调度预期而产生的平均运行熵为Cda:
(7)
即在调度时限T内,由于实际生产过程中存在的各类扰动,调度方案中所包含的结构熵C′ss以平均Cda的速率向运行熵转化。因此,预制混凝土构件生产系统最大可行调度时限为:
(8)
当预制混凝土构件生产系统运行到Tmax时,初始调度方案中的结构熵全部转化为运行熵,该时限以后实际生产将完全偏离调度预期,必须进行再调度。由此可见,预制混凝土构件生产系统再调度时刻不能晚于最大可行调度时限;否则,再调度时刻就是不合理的。
2.2 评估调度符合程度
生产调度方案在实际运行过程中未发生偏离部分所包含的剩余结构熵,可以用相对值A表示,如式(9)所示。该值能够用来衡量调度的符合程度,其值越大,表明调度的实际执行情况与原调度方案的符合程度越高,即调度方案对于实际生产的指导性越强。

(9)
综上所述,最大可行调度时限与调度符合度构成了对预制混凝土构件生产系统状态评估的两项指标。一方面参考最大可行调度时限设置合理的再调度时刻及时进行生产纠偏,另一方面通过分析引起调度符合度下降的系统状态,有针对性地改善调度效果。
3 实例分析
从全供应链视角出发[24],预制混凝土构件的生产可分解为八个步骤,如图1所示,分别为:(1)模具处理;(2)安放钢筋和预埋件;(3)混凝土浇筑;(4)固化养护;(5)脱模;(6)质检和表面处理;(7)构件存放;(8)构件运输。此外,在制定生产调度方案时还需考虑工序性质、工人工作时间、运输方案,以及模具数量和养护空间等具体约束[24]。

图1 预制混凝土构件生产八工序流程

图2 预制混凝土构件生产调度方案甘特图
以某混凝土预制构件厂为研究对象,图2为该厂某条流水线五个构件的生产调度方案甘特图。在该案例中,工人每天正常工作10 h;模具数量充足,养护与存放空间充足;运输方案采用紧急订单全天运输,即构件运输工序开始时间不受工人工作时间限制,一旦预制构件强度达到吊装运输要求便可开始;调度时限为72 h,调度精度为1 h。在图2中,I表示设备空闲,N1~N8分别表示预制混凝土构件生产八道工序的预期生产状况。在实际生产执行过程中记录各项工序的实际起止时刻(包含了显性扰动和隐性扰动),得到该生产调度方案的实际执行情况甘特图如图3。其中,N1′~N8′分别表示八道工序的实际生产状况,R1~R3分别表示因模具、钢筋及混凝土资源供应延迟而造成的等待状况,R4表示因运输设备延迟而造成的等待状况,F表示因设备故障而造成的等待状况。

图3 预制混凝土构件生产调度方案实际执行情况甘特图
3.1 调度方案的结构熵
取图2所示生产调度方案中所有预期发生的离散事件作为预制混凝土构件生产系统的状态。以第1个预制构件为例,取图2中72 h的调度数据作为依据,根据不同状态的预期持续时长ti计算各状态发生概率pi(pi=ti/72),计算结果如表1。根据式(2)求得第1个预制构件的结构熵为2.15368 bit(bit为以2为底的对数的信息量的单位)。

表1 构件1结构熵计算
同理进行其余构件的结构熵计算。特别地,在本案例中,因构件种类相同,且在调度时限内各构件的对应状态预期持续时长相同,因此各构件的结构熵相同,均为2.153677 bit。
根据式(6),可求得该调度方案的平均结构熵为:
3.2 调度方案的运行熵
为便于对比分析,取与结构熵计算中相同粒度的所有偏离调度预期的状态,作为计算预制混凝土构件生产系统运行熵的异常状态,可能出现的异常状态如表2所示(表中各类超时异常状态均为工人加工时间波动、设备使用率下降等隐性扰动共同作用的结果)。同样地,以图3中第1个预制构件为例,计算各异常状态发生概率p′i(p′i=t′i/72),并按照式(5)求得第1个预制构件由于偏离调度预期而产生的运行熵为0.793254 bit。
同理计算其余构件由于偏离调度预期而产生的运行熵,结果依次为0.928739,0.591729,0.506036,0.460965 bit。

表2 构件1运行熵计算
再根据式(5)求得该预制混凝土构件生产系统在任一运行时刻由于偏离调度预期而产生的运行熵为:
Cdd=0.793254+0.928739+0.591729+0.506036+0.460965=3.280723 bit
根据式(7),可得到该预制混凝土构件生产系统在调度期内平均运行熵为:
3.3 调度有效性分析
根据式(8),可求得该预制混凝土构件生产系统的最大可行调度时限为:
即可以一次编制最长连续236.3 h(约10 d)的生产调度计划,这意味着,在该预制构件连续生产过程中,再调度的时刻不能迟于236.3 h。
根据式(9),可求得在当前生产扰动存在条件下,调度符合度为:
=69.53%
即在该预制构件的实际生产过程中,只有69.53%的调度结构熵按预期得到了执行,而剩余30.47%的结构熵则由于生产扰动转化为运行熵。

表3 实际生产过程中不同异常状态引起的运行熵
进一步挖掘调度符合度不达预期的主要原因。通过与如表3所示的由不同异常状态引起的运行熵进行比较可以发现,其中影响最大的三点因素为设备故障、运输超时以及运输设备延迟,分别占该预制混凝土构件生产系统因偏离调度预期而产生的总运行熵的14.93%,12.81%,12.29%。重点对该预制构件厂相关环节进行调查后发现:该厂养护窑老旧导致设备故障频发,需即刻换新;受新冠疫情影响该厂人员变动大,雇佣了一批新运输司机与装卸工人,不熟悉运输路线与装卸流程导致运输超时与运输设备延迟到位,急需开展运输与装卸培训。在采取上述调整与改进措施,使得前述3项异常状态的发生时长明显降低,并在暂不对其他异常状态进行处理的条件下,调整后该预制混凝土构件生产系统运行熵计算结果如表4所示(以第1个预制构件为例)。

表4 调整后构件1运行熵计算
同理进行其余构件运行熵的计算,并根据式(5)(7)计算出调整后:
Cdd=0.649645+0.458605+0.314996+
0.314996+0.229302=1.967544 bit
根据式(8),调整后该预制混凝土构件生产系统的最大可行调度时限为:
同样地,根据式(9),调整后该预制混凝土构件生产系统的调度符合度为:
=81.73%
对比调整前后的结果可见,该预制混凝土构件生产系统的最大可行调度时限延长了50%以上,且其调度符合度上升为81.73%,即由于生产扰动而转化为运行熵的信息熵降为18.27%。这直观反映出通过聚焦异常状态进行针对性调整,可以有效控制预制混凝土构件实际生产过程中调度方案的偏离程度。
为验证预制混凝土构件生产系统状态评估指标在不同规模案例应用中的有效性,本文引入了16个构件、调度周期为7 d(168 h)的中规模生产调度案例与32个构件、调度周期为11 d(264 h)的大规模生产调度案例,计算结果如表5所示。两个案例中最大可行调度时限与调度符合度分别为242 h,30.82%(即经过168 h的运行后,仅剩余30.82%的系统结构熵还未发生偏离,此时调度周期168 h虽未超过最大可行调度时限242 h,但调度符合度偏低,可考虑提前进行再调度),以及258 h,-2.3%(此时调度周期264 h超过了最大可行调度时限258 h,即经过264 h的运行后,系统实际运行已完全偏离调度预期,调度符合度为负值,必须提前再调度)。上述小规模、中规模、大规模的三个混凝土预制构件生产调度案例的实际应用结果表明,本文提出的最大可行调度时限与调度符合度两项量化指标,可以用于评估不同规模的预制混凝土构件生产系统状态。
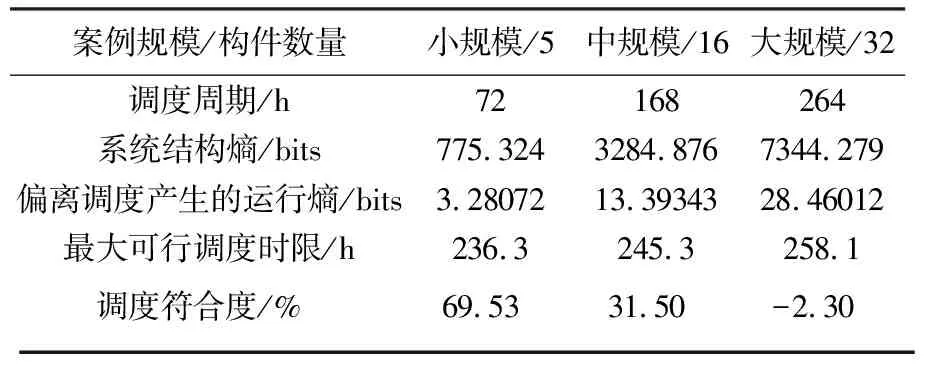
表5 不同规模案例计算结果
4 结 论
(1)预制混凝土构件生产过程中的生产扰动会使生产系统实际运行偏离调度,在需考虑隐性扰动的实际生产中缺少合理纠偏时刻的确定工具;
(2)为实现对预制混凝土构件生产系统状态的度量,合理地制定再调度时刻与系统运行优化策略,本文以信息熵理论为基础,搭建了预制混凝土构件生产系统的结构熵与运行熵模型,提出了最大可行调度时限和调度符合度两项量化评价指标;
(3)应用实例分析结果表明,所构建的结构熵与运行熵模型,以及最大可行调度时限和调度符合度等量化指标可有效实现对考虑隐性扰动的预制混凝土构件生产系统状态的监测评估,为再调度时刻的合理制定提供依据,为有针对性地提高系统运行效率与调度有效性提供参考。
