基于GSA-IFCM的单位周期时间序列自适应提取方法

闫啸家，梁伟阁，张 钢，田福庆

(海军工程大学，湖北 武汉 430033)

0 引言

中大口径舰炮供输弹机构在运转过程中通常作循环往复式运动，过程复杂且常伴有剧烈的冲击、摩擦和振动，其工作健康状态一直是制约供输弹机构性能和实用性的障碍，也成为机械装备状态监测与故障诊断领域的焦点[1]。对其健康状态进行评估的前提是状态监测数据的采集，在严格的数学意义上监测数据是非周期、非平稳的随机信号，但是从宏观角度考虑工作原理及过程，在连续运行时，监测数据表现出明显的近似周期性。因此，供输弹机构的振动信号是典型的近似周期信号。

近似周期信号是一种特殊的近似周期时间序列。目前，对于近似周期时间序列的周期估计和提取问题，文献[2]首次分析了近似周期时间序列，给出了详细的数学定义，并提出了运用矩估计法对时间序列的周期进行估计；文献[3]采用拟合估计法对已有时间序列数据提取能够反映时间变换的二维数据，更加真实地反映了近似周期时间序列的周期性变化。以上方法对于变化范围小的近似周期时间序列效果较好，而供输弹机构循环往复、工作节拍不一致且瞬间冲击较大，其信号振幅瞬变且变化范围大，导致无法有效提取单位周期时间序列。文献[4]运用相位差频谱校正-互相关法对谐波减速器的近似周期振动信号分割构造出单位周期数据样本以准确刻画减速器的运行状态信息，但是该方法只针对包络线近似为正弦曲线且频率稳定的旋转机械周期振动信号，而往复机械的近似周期冲击信号由于瞬时幅值较大，无法通过准确的数学曲线方程有效构建包络线，其自适应提取方法研究甚少，多数还需要人工截取单位周期时间序列，依赖于专家经验且效率低下。本文针对上述问题，提出基于GSA-IFCM的单位周期时间序列自适应提取方法。

1 IFCM, SA和GA算法

1.1 改进模糊C均值聚类算法(IFCM)

设X={x1,x2,…,xn}为n个时间序列，{A1,A2,…,Ac}表示此时间序列的c个类别，U是其相似分类矩阵，{v1,v2,…,vc}为各类别的聚类中心。则目标函数Jb为：

(1)

(2)

设Ik={i|2≤c≤n;dik=0}，对于所有的i类，i∈Ik,uik=0，则更新聚类中心vij的迭代方程为：

(3)

FCM其实是寻找一种最佳的分类，以使该分类能产生最小的函数值Jb。它要求一个样本对于各个聚类的隶属度值和为1，即：

(4)

用式(2)和式(3)反复修改聚类中心、类别隶属度，然后进行再次分类，当算法收敛时，理论上就得到各类的聚类中心以及各个样本对于各对应类别的隶属度，从而完成模糊聚类划分。尽管FCM有很高的搜索速度，但是FCM是一种局部搜索算法，且对聚类中心的初值十分敏感，一旦初值选取不当，它就会收敛到局部极小点[5]。

算法中目标函数Jb的加权参数b依赖人为经验选取，如果聚类中心过多、数据噪声较大，不易产生理想的聚类中心，因此，为了避免参数b选择的盲目性以及提高聚类的精确度，提出以聚类中心横坐标的方差作为评价标准迭代计算从而寻找最优加权参数的改进方法，其计算公式为：

(5)

综上所述，IFCM算法是通过改进模糊C-均值聚类算法，迭代计算聚类中心横坐标的方差以不断修正聚类中心，最终得到横坐标分布最平均的聚类中心。

1.2 模拟退火算法

模拟退火算法(simulated annealing, SA)是通过模拟高温物体退火过程找到优化问题的全局最优或近似全局最优解[6]。具体步骤如下：

1) 设置初始温度、终止温度、冷却系数等，随机产生一个初始温度S0，令S(0)=S0；

2) 在当前解的邻域中，以概率P(T)选择一个非局部最优解，之后计算该解与上一个最优解的能量差，若差值大于0，则重新选择最优解，否则将该解作为下一个当前解；

3) 按照一定方式降温后，检查是否达到终止条件，如果满足则转至步骤4)，否则转回步骤2);

4) 结束迭代，当前解为最优解，输出结果。

1.3 遗传算法

遗传算法(genetic algorithm, GA)是一种进化算法，基本原理是效仿生物界的“物竞天择、适者生存”的演化法则。主要思想是将问题参数编码为染色体，再利用迭代的方式进行选择、交叉和变异等运算来交换种群中染色体的信息，以达到最终生成符合优化目标染色体的目的。其详细过程见文献[7]。

2 基于GSA-IFCM的单位周期时间序 列自适应提取方法

手动截取单位周期时间序列耗时耗力，若以某一单位时间序列的周期将整个时间序列等长度分段截取，或者以若干单位时间序列周期的均值截取，由于数据噪声以及非线性的影响，会导致单位时间序列数据失真、故障信息丢失。

通过GSA算法与IFCM算法相结合，提取近似周期信号单位时间序列极大值的聚类中心，然后运用t-MSV算法，通过设置时间窗计算时间序列能量曲线以确定单位周期时间序列的起止位置，从而提取单位周期时间序列。方法具体流程如图1所示。

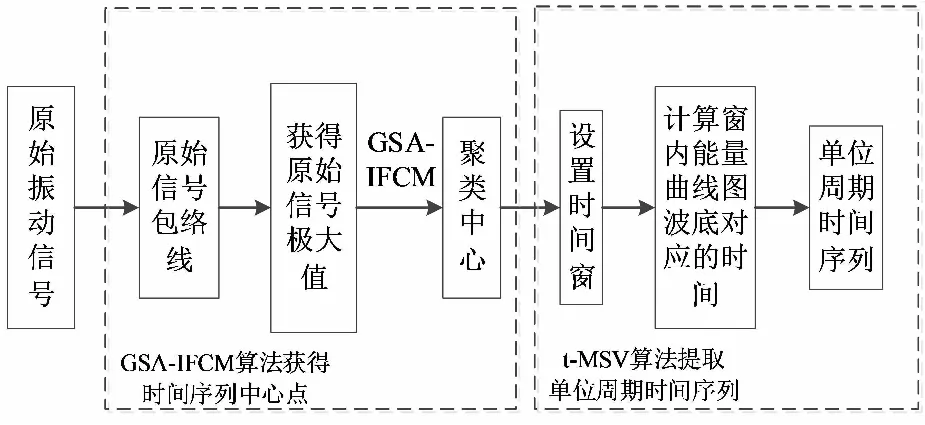
图1 单位周期时间序列提取方法流程Fig.1 Flow chart of unit cycle time series extraction method

2.1 单位周期时间序列中心点搜寻方法

GSA算法本质是将GA和SA算法结合起来，产生一种新的混合优化算法[8]，它可以充分发挥SA算法较强的局部搜索能力和GA算法较强的全局搜索能力，有效克服传统GA算法的早熟现象；IFCM算法本质上是一种局部搜索优化算法，它改善了参数选择的盲目性以及提高聚类的精确度。

将GSA和IFCM算法相结合可以相互取长补短，有效、快速识别出每个单位周期时间序列的中心点。获取单位周期时间序列中心点的具体步骤如下：

1) 通过在非扭结边界条件(not-a-knot spline)下对相隔不变数量采样点的局部最大值进行分段样条插值，以生成原始振动信号平滑的峰值包络线。

2) 提取峰值包络线极大值，进而求得可以表征原始信号变化趋势的有效极大值点，达到减少计算量的目的。

3) 以极大值点的横纵坐标作为输入向量，同时设定类别个数，通过GSA-IFCM算法迭代计算并不断修正聚类中心，直至得到最优聚类中心，从而得到单位周期时间序列中心点。

由上述步骤可以看出，GSA-IFCM算法是获取聚类中心点的关键，其流程图如图2所示。

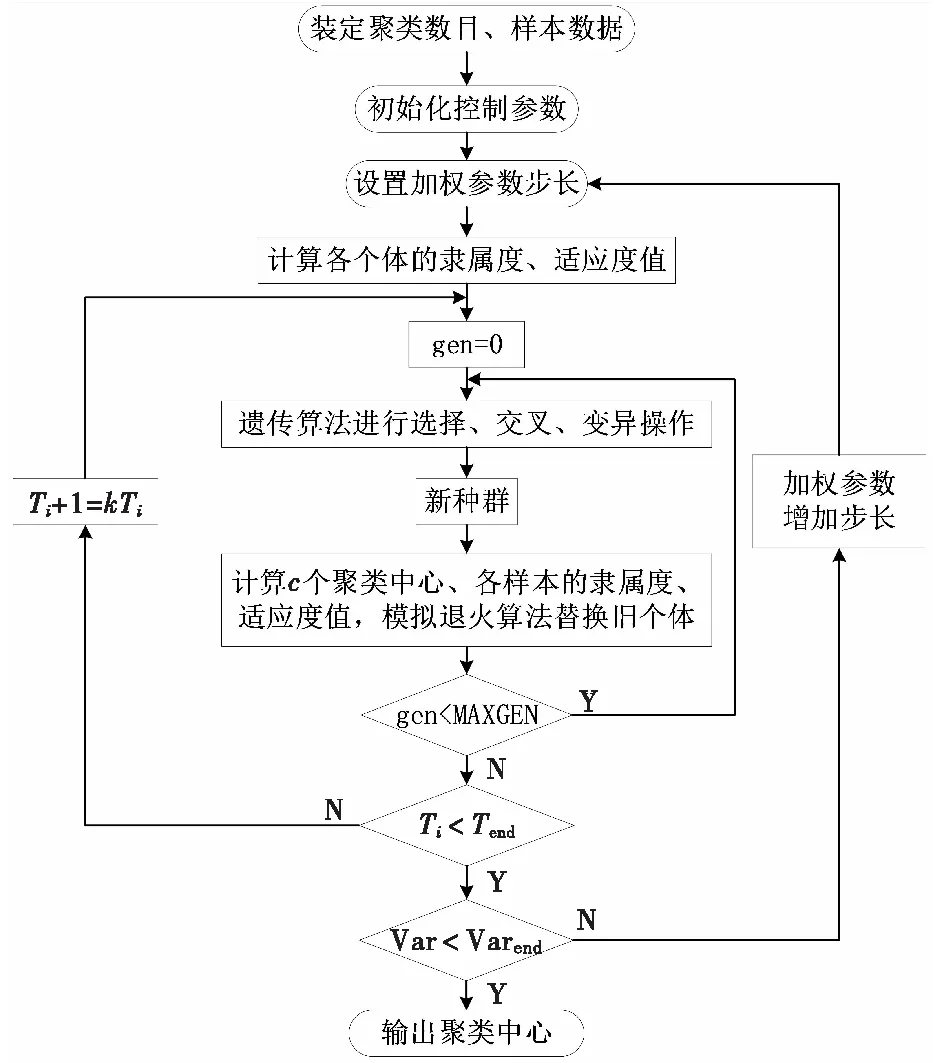
图2 GSA-IFCM算法流程图Fig.2 Flow chart of GSA-IFCM algorithm

2.2 单位周期时间序列提取方法

获取中心点后，向中心点前后方向获取单位周期时间序列的长度，向前获取样本长度的具体步骤如下：

1) 设置足够小宽度的时间窗，以时间窗宽为步长，以聚类中心为起点向前循环计算窗内时间序列的能量值。表征信号能量值的参数均方值计算公式为：

(6)

当均方值单调递增时，说明信号的能量在升高，处于冲击震荡阶段；当均方值单调递减时，说明信号的能量在下降；当均方值稳定在某一个值后，说明信号的能量趋于平稳，因此每个波峰对应的波底是冲击信号起始与结束的位置。

2) 计算时间窗能量曲线图波底对应的时间，设定相应阈值，若时间窗能量在阈值内未能检测到能量上升，则判定此波底为最终波底，此波底对应的时间即为周期时间序列的最优起始位置。

3) 向后获取样本长度同上，获得聚类中心前后方向样本长度即可准确提取单位周期时间序列。

上述单位周期时间序列提取方法称为时间窗能量法(t-MSV),即通过设置足够小宽度的时间窗计算时间序列能量曲线，设定阈值寻找最终波底以确定单位周期时间序列的起止位置，从而提取单位周期时间序列。

3 试验及结果分析

3.1 试验介绍

本文试验数据采集自某型供输弹机构试验台架，如图3所示。

图3 供输弹机构试验台架Fig.3 Test bench for bomb feeding mechanism

试验在台架装置的摆动机滑板，位于滚轮上方的压板机附近布置了6个振动加速度传感器，传感器类型为ICP加速度传感器，采样频率为10 kHz，采用32通道的LMS信号采集系统。分别采集正常工作、滚轮裂纹和滑板磨损三种状态下共24组振动加速度信号，每组信号包含20个循环动作。3种状态振动加速度信号的时域波形如图4所示。

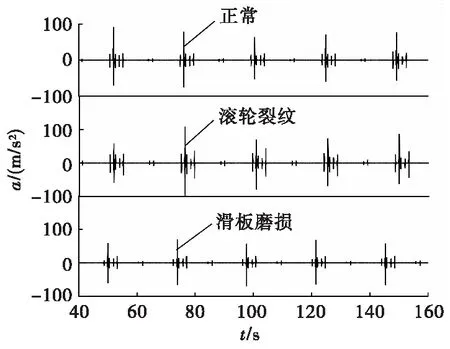
图4 加速度信号的时域波形图Fig.4 Time domain waveform of acceleration signal

由图4可知，供输弹机构测得的振动加速度信号有较大的冲击振动，其中滚轮裂纹状态下冲击最为显著。同时，仅从原始振动加速度信号来看，每一个单位周期时间序列的周期长度和最大幅值均不为固定值，且相邻周期的间隔均不相等，所以无法使用一个固定周期循环提取单位周期时间序列。

3.2 试验台架振动信号自适应提取方法

将本文提出的提取方法应用于上述试验数据，选取正常工作状态下的振动信号，具体步骤如下：

1) 对间隔为200个采样点的局部最大值进行分段样条插值，生成原始振动信号平滑的峰值包络线如图5所示。图中剧烈振荡曲线为原始振动信号，连续平稳曲线为包络线。

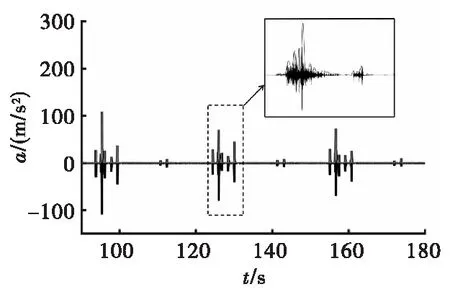
图5 原始信号和包络线Fig.5 Raw signal and envelope

2) 提取峰值包络线极大值，进而求得原始信号的有效极大值点，如图6所示，该方法不要求曲线通过所有的已知点，保证曲线与信号变化趋势一致即可。图中包络线极大值点的数量明显小于原始信号极大值的数量，以此来提高计算速度。

图6 原始信号和极大值点Fig.6 Original signal and maximum point

3) 利用GSA-IFCM算法，以极大值点的横纵坐标作为输入向量，同时设定类别个数，通过不断迭代计算获得极大值点的最优聚类中心，以此来获取单位周期时间序列中心点，如图7所示。

图7 极大值点和聚类中心Fig.7 Maximum point and cluster center

4) 通过不断试验，选取窗宽为0.01 s的时间窗。由聚类中心向前循环累加时间窗，如图8所示。

图8 原始信号加窗Fig.8 Windowing the original signal

5) 通过对比采用其他时域特征方差和峰值，选取均方值以表征时间窗内时间序列的能量，获得能量曲线图，如图9所示。图中包含3个波峰，与中心点左侧存在3次冲击相对应。

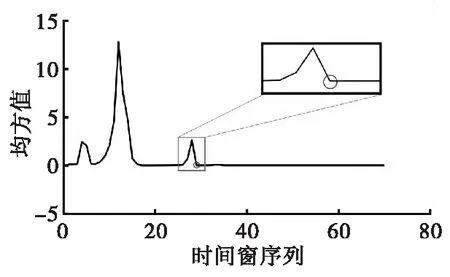
图9 能量曲线图Fig.9 Energy curve

6) 设定时间窗阈值k=100，若时间窗能量在阈值内未能检测到能量上升，则计算时间窗能量曲线图最后一个波峰波底对应的时间(如图9圆圈所示)，即为单位周期时间序列的起始位置。

按照上述步骤以聚类中心为起点向右计算单位周期时间序列的结束位置，即可提取整个单位周期时间序列，如图10所示。

试验中一个完整的往复运动时间约为6.8 s，每个波峰分别对应动作为：复进—起摆—回摆—关闩，采用本方法可以有效实现机构运动状态的准确复现。

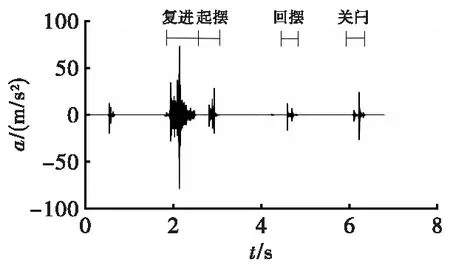
图10 单位周期时间序列Fig.10 Unit period time series

3.3 试验结果分析

每项状态下采集到的近似周期振动信号利用本文方法均可有效提取出单位周期时间序列。试验中SA算法设置冷却系数q=0.8，初始温度T0=100，终止温度Tend=1。GA算法的相关初始参数如表1所示。

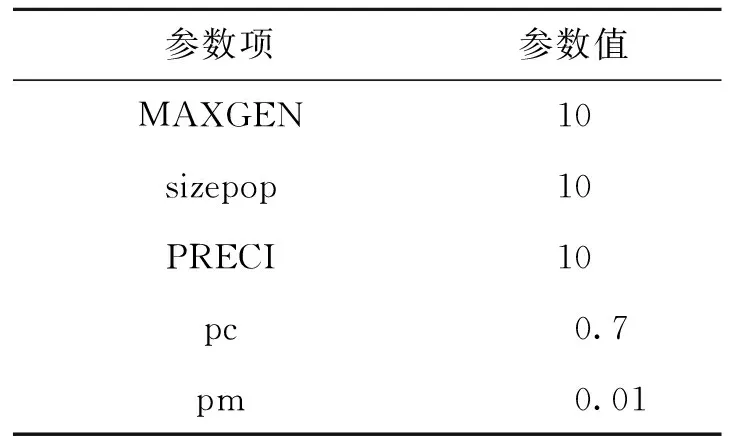
表1 GA算法相关参数表Tab.1 GA algorithm parameter

为验证本文方法的有效性，分别通过使用标准的FCM算法、基于GSA的FCM算法以及基于GSA的IFCM算法对三种健康状态下的1组近似周期振动信号极大值进行聚类，每种状态下振动信号聚类中心与单位时间序列中心点的时间距离曲线图如图11所示。若距离小于单位时间序列的一半(图11中垂直于纵坐标的直线)，则认为该聚类结果正确。

图11 时间距离曲线图Fig.11 Time distance graph

观察图11可知，采用标准的FCM算法对大规模数据进行聚类处理，由于其对初始中心选取较为敏感，更加容易收敛到局部最优解，不能有效地对原始信号的极大值进行均匀聚类。利用基于GSA的FCM算法对三种振动信号极大值进行聚类，虽然聚类中心近似均匀分布，但由于加权参数取值模糊，仍有陷入局部极小点的可能性，例如图11(b)中有2个聚类中心点异常；而运用GSA-IFCM算法可有效克服数据噪声的影响，准确提取各周期时间序列的中心点，出现过早收敛的可能性极小，所获得的聚类结果具有更强的稳定性和更优的目标函数值，对于随机分布的数据聚类有明显的优越性。

试验共采集三种状态下各8组振动加速度信号，每组20个循环动作，即三种状态下各160个循环动作。每组原始信号的聚类结果正确个数与准确度如表2所示。

表2 聚类结果的准确度Tab.2 Accuracy of clustering results

由表2可知，采用3种不同的方法，正常状态下的聚类准确度均高于滚轮裂纹和滑板磨损，原因是正常状态下振动信号的噪声较小，对算法的影响较小。滚轮裂纹状态下准确度略低的原因是此状态下振动最为剧烈，峰-峰值可达900g，但运用GSA-IFCM算法依然可以达到较高的准确度。

为了验证采用时域特征均方值来表征时间窗能量的优势，分别利用24组正常状态、滚轮裂纹和滑板磨损下的振动信号，将均方值与采用其他归一化时域特征方差和峰值进行对比，其中，GA与SA算法参数设置与上述相同。利用3种时域特征对3种状态下测试样本提取单位周期样本序列，并重复试验10次的平均准确度柱状图如图12所示。

由图12可知，采用峰值和方差特征参数时，仅描述信号值的变化范围和离散趋势，对信号离散程度小的区段描述较弱，难以确定信号的起止范围，从而导致单位周期样本序列的提取平均准确度较低；而采用均方值对正常状态、滚轮裂纹和滑板磨损下提取单位周期样本序列的平均准确度分别可达98.31%、96.88%、97.75%，说明该特征可以准确描述信号的振动过程，有效表征其能量变化规律，因此，与采用峰值、方差等其他的时域特征参数对信号进行提取相比较，利用均方值表征时间窗能量可以准确提取出单位周期时间序列。

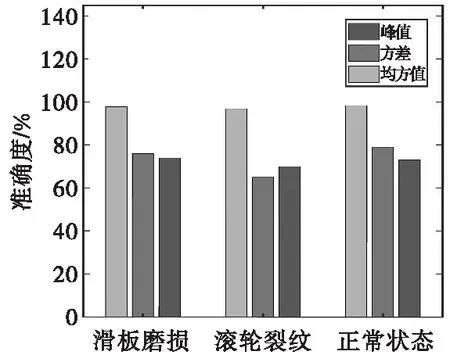
图12 3种时域特征对3种状态下测试样本提取 单位周期样本序列的平均准确度Fig.12 Extraction of three time-domain features for test samples in three states average accuracy of a sequence of samples per unit period

4 结论

本文提出基于GSA-IFCM的单位周期时间序列自适应提取方法。该方法通过GSA算法与IFCM算法相结合，提取近似周期信号单位时间序列极大值的聚类中心，然后运用t-MSV算法，通过设置时间窗计算时间序列能量曲线以确定单位周期时间序列的起止位置，从而提取单位周期时间序列。试验结果表明： 1) 利用GSA与IFCM相结合的方法，可有效克服数据噪声的影响，聚类结果具有更强的稳定性和更优的目标函数值，对于随机分布且包含噪声的数据聚类有明显的优越性；2) 通过时间窗求取信号的时域特征参数均方值可表征信号的能量趋势，相比于其他时域特征参数可有效展现出原始信号的振动规律，能够准确提取出单位周期时间序列。