基于航向角辅助的IMM-CKF雷达/红外跟踪算法
2022-05-13李世中
彭 滔,张 亚,李世中
(中北大学机电工程学院,山西 太原 030051)
0 引言
随着现代战争的高速发展,地面探测器与高速机动目标的较量日渐呈现出白热化状态。高机动目标的特点决定了仅靠单一种类的探测器难以快速且连续地探测、跟踪目标,需要综合应用多装备协同实现对目标有效地探测、跟踪[1]。雷达作为传统有源传感器,可以提供完整的目标位置信息,故在目标检测及跟踪方面发挥着不可磨灭的作用。但由于雷达在工作中需要向空中辐射高功率电磁波,易受到电子和反辐射导弹的袭击[2-3]。红外传感器作为被动传感器通过接收目标辐射的热能来检测和定位目标,同时具有较强的抗干扰能力,但作用距离短是红外传感器的短板[4]。将雷达和红外传感器的量测数据通过数据融合技术结合在一起形成雷达和红外多传感器探测系统,可有效地弥补各自缺点,从而给出目标位置的精准估计。
文献[5]中首次将序贯滤波的方法加入到雷达红外复合制导系统中,在此基础上加入交互式多模型来跟踪复杂的机动目标,但没有解决序贯滤波本身的误差累计的问题。文献[6]中将分布式加权融合算法与交互式多模型无味卡尔曼滤波(IMM-UKF)算法结合,该方法提高了系统抗干扰能力和对目标跟踪的有效性,但该算法只适用于低维非线性系统且实时性不足。文献[7]提出了一种雷达辅助的红外传感器融合系统,该系统利用雷达工作时获得的目标状态信息作为辅助信息传递给红外传感器,从而提高跟踪性能。文献[8]提出了基于IMM-CKF的纯角度测量的机动目标跟踪算法,该算法利用角度测量来跟踪机动目标,其跟踪性能明显优于IMM-UKF滤波算法,对非线性系统机动目标跟踪,该算法不仅提高了目标跟踪滤波精度,而且增强了系统稳定性。文献[9]中目标的航向信息能直接反映目标飞行朝向,故研究对航向信息的解算,以及利用航向信息作为辅助信息进行目标跟踪具有十分重要的工程意义。针对传统雷达传感器的非线性机动目标跟踪中,采样信息差异和目标机动强等原因造成的跟踪性能低等问题,本文提出基于航向角辅助的IMM-CKF雷达/红外跟踪算法。
1 雷达红外复合系统与容积卡尔曼滤波
1.1 雷达红外量测模型
假定雷达与红外传感器系统同地配置,已经过坐标转换,其目标的离散信号模型可以表示为:
X(k+1)=F(k)X(k)+G(k)u(k)+V(k),
(1)
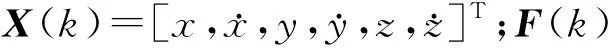
因为雷达可以测量出机动目标的三个参数,分别为:距离、方位角和俯仰角,因此设rR(k)、θR(k),φR(k)分别为目标距离、方位角以及俯仰角,测量噪声为νrR(k)、νθ R(k)、νφ R(k),其测量方程为:
(2)
令θI(k)和φI(k)分别为红外传感器测量目标的方位角和俯仰角,νθI(k),νφI(k)为测量噪声,其测量方程为:
(3)
因在航向角的计算中是在X-Y的二维平面中求解,式(2)、式(3)中的俯仰角参数对后续的参数计算无影响,故后续求解不予以考虑。
1.2 容积卡尔曼滤波
容积卡尔曼滤波(CKF)基于三阶球面径向容积准则,并使用一组容积点来逼近具有附加高斯噪声的非线性系统的状态均值和协方差。本章节总结了CKF滤波算法,该算法在每个时间步长中计算时间更新和量测更新步骤。
CKF滤波算法具体步骤如下:
1) 初始化
(4)
2) 时间更新
①计算容积点:
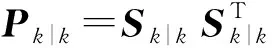
(5)
(6)
式(6)中,i=1,2,…,2n,且ξi为第i个容积点。
(7)
式(7)中,n为状态变量的维度,[1]为单位矩阵。
②传播容积点:
(8)
③计算状态量预测值及误差协方差预测值:
(9)

(10)
3) 量测更新
①计算容积点:
(11)
(12)
②传播容积点:
(13)
③计算测量预测值:
(14)
④测量误差协方差和互协方差:

(15)

(16)
⑤更新增益、状态量、误差协方差:
(17)
(18)
Pk+1|k+1=Pk+1|k-Wk+1Pzz,k+1|k(Wk+1)T。
(19)
2 二维航向角与IMM-CKF滤波算法
2.1 二维航向角的定义与求解
在三维空间中,航向角是机动目标的速度向量在水平面上的投影,是其投影与某一基准方向的夹角。在本文中采用直角坐标系中将机动目标的速度向量与y轴的正方向作为航向角的基准方向,且记顺时针方向为正。
在实际跟踪过程中,由于测量噪声的影响,使得测量航向角与目标航向角之间必然存在偏差。而由于测量噪声引起的偏差可以通过滤波方法或提高探测精度进行削弱。所以,本文利用量测航向角信息来对目标航向角信息进行修正,从而提高系统的估计精度。
(20)


(21)

(22)
在滤波的过程中,通过k时刻的滤波值得到k+1时刻的预测值,并将其转换成测量预测值,根据复合测量值与预测值计算复合新息,利用容积卡尔曼滤波(CKF)算法得到k+1时刻的滤波值,并由此来更新航向角。
2.2 基于IMM-CKF的融合算法
基于IMM-CKF的雷达/红外算法的核心思想是把在交互式多模型中的雷达和红外部分分别利用容积卡尔曼滤波(CKF)对量测信息进行滤波[10-12]。算法框图如图2所示。

图2 IMM-CKF算法框图Fig.2 IMM-CKF structure
算法具体内容包括以下步骤:
1) 计算混合概率

(23)

(24)
2) 计算交互/混合状态估计和协方差
(25)

(i,j=1,2,…,r),
(26)
3) 模型滤波
4) 模型概率更新
r个模型滤波器的似然函数可能为:
(27)
此时,模型Mj的概率更新为:
(28)
(29)
式(28)、式(29)中,c为归一化常数。
5) 计算状态估计及其协方差
根据混合方程计算输出状态估计和协方差为:
(30)

(31)
3 仿真实验
3.1 目标模型集
为了验证基于航向角辅助的IMM-CKF跟踪算法的可行性,本文假定目标运动由三个模型(r=3)组成。
M1:匀速模型(CV)
CV模型用于目标处于非机动时段。目标状态为:
(32)
离散状态转移矩阵为:
(33)
M2:协调转弯模型(CT)
在这一模型中,用一个角速度ω来增加状态向量,假定角速度ω恒定不变,目标状态可以表示为:
(34)
离散状态转移矩阵为:

(35)
M3: 对ω<0时,M2模型描述一个顺时针转弯运动,此模型为一逆时针转弯运动,即为ω>0。
3.2 仿真参数设定


目标1的初始状态为[8 000 m,200 m/s,5 m/s2;5 000 m,400 m/s,1 m/s2;9 000 m,250 m/s,10 m/s2],目标2的初始状态为[1 000 m,120 m/s,0.5 m/s2;6 000 m,-300 m/s,0.5 m/s2;5 000 m,-100 m/s,15 m/s2]。
3.3 仿真结果分析
图3所示为计算机仿真建立的目标1、目标2的运动轨迹和雷达-红外融合跟踪滤波轨迹的对比图。从图中可以看出在整个观测时间内,本文提出的算法能很准确地确定目标的运动轨迹。图4、图5分别为目标1、目标2同时在基于航向角辅助下的两个坐标方向上使用雷达单传感器与融合跟踪滤波在位置上RMSE值的对比结果。从图4与图5中可以看出雷达和红外传感器融合后对目标跟踪的RMSE值明显低于雷达单传感器,且整个RMSE值表现平稳,没有大幅度的变化,表明本文提出的基于航向角辅助的IMM-CKF滤波算法对机动目标的跟踪有效且适用。同时由图6可以看出采用融合系统能够综合各单传感器的优势,复合探测系统对提高航向角的估计精度有着积极作用,实现量测信息互补,精确估计目标状态。

图3 目标机动轨迹Fig.3 Target maneuvering trajectory

图4 目标1在x方向和y方向的位置误差Fig.4 Objective 1 x-direction and y-direction position error

图5 目标2在x方向和y方向的位置误差Fig.5 Objective 2 x-direction and y-direction position error

图6 航向角的RMSE值Fig.6 RMSE values for course angle
4 结论
本文提出基于航向角辅助的IMM-CKF雷达/红外目标跟踪算法。该算法充分利用多传感器的互补效应,利用红外传感器的量测信息作为首层辅助信息来修正雷达的量测信息,用该信息对目标速度的方向进行更新,从而达到提高目标跟踪精度的目的。同时提出将航向角信息引入到IMM-CKF滤波中来,利用航向角信息作为第二层辅助信息来与雷达和红外传感器的复合测量信息求出目标的测量航向角,随之将更新的航向角信息与雷达和红外传感器的量测信息组合,共同组成全新的复合量测向量,同时目标预测状态向量也增加航向角分向量,该航向角即为目标速度向量的方向,最后利用IMM-CKF滤波算法进行滤波。仿真实验结果表明,基于航向角信息辅助的IMM-CKF雷达/红外目标跟踪算法能够显著提高对目标的跟踪精度,同时利用复合探测也有效提高对航向角的估计精度。
