融入直播方式的电商供应链最优决策研究

申 彦，敬露艺，袁 圆 （江苏大学 管理学院，江苏 镇江 212013）

0 引言

近年来，随着直播的出现，“电商+直播”的模式逐渐开始发展。与传统电商模式不同的是，直播模式下的电商将商品信息由原来的图片或视频展示转变到现在的直播演示，以主播亲自体验商品的方式让消费者更好的全方位了解商品，在很大程度上刺激了消费者的购买欲望，直播电商模式愈加受到消费者的青睐。

电商销售模式的兴起不仅受到来自民众与业界的关注，还成为了学术界的研究热点。当前不少学者在电商供应链决策问题上展开了深入研究。He等分析了三种在线销售模式，通过博弈模型分析TSC及成员的最优销售模式和定价决策。Zhong等基于Stackelberg理论研究电商商城和物流两阶段物流服务供应链，制定利润分配的契约，通过物流服务与供应链之间合作达到利润最优。He等考虑电商供应链中双渠道LSS竞争问题，研究发现，零售商价格的高低取决于物流的优质问题。田晨等研究了制造商对销售模式选择以及平台物流模式，研究发现，制造商选择不同的平台模式取决于平台是否提供物流服务。Qin等分析了电商中物流服务共享的影响，研究表明若市场潜力和服务水平较低时，会出现平台与卖方双赢局面，当市场潜力和服务水平较高时，会出现平台与卖方双输局面，当服务水平和市场潜力处于中等情况时，会出现双赢的局面。肖迪、方慧敏等在电商平台赋能情况下，对信息不对称进行研究。研究表明平台型电商通过设计混合分离策略来激励零售商订购数量，若零售商通过其他渠道订购数量越高时，平台型电商的分离策略可以提高零售商的订货量，反之则使用混合策略。Chen等对平台收益进行分析，研究表明广告模式占有比例决定平台收益，考虑在广告高比例时，平台上匹配概率高低对平台的影响。士明军、王勇等研究了电商—物流—平台之间的决策，研究表明在不同的市场能力结构下，各主体投入决策的改变会对另外两个主体造成不一致的影响。Wei等从顾客接受度角度出发，构建了制造商和零售商博弈模型，以增加零售商的利润流来提高制造商的盈利能力。洪定军、范建昌等分析了电商供应链系统的最优决策问题，研究发现分散决策偏离会使系统利润受到损失。Wang等研究了制造商和第三方电子商务平台组成的电商供应链，结果表明利他偏好有利于提高制造商的销售水平和销售量。

综上可知，针对电商供应链决策问题，学者从供应链利益、消费者受益度、收益共享契约等方面均做了相关研究，然而当前研究范围局限于传统电商的供应链管理，对于直播模式下的电商供应链涉及较少。

基于此，本文在融入直播方式背景下，构建“供应商—直播方零售—消费者”与“供应商—直播方代理—消费者”两种直播电商供应链模型，分别进行博弈与均衡分析，以期求得供应链的最优决策。当前直播电商模式主要分为两种，一种是直播方从供应商处批发商品，再借助直播平台进行直播带货，即直播方充当零售商的角色，如抖音平台里的部分直播方。另一种是供应商与直播方进行合作，直播方在直播平台上为其代销商品，商品价格由供应商决定，直播方不参与决策，这种模式常见于淘宝、天猫等平台。

1 模型构建

表1 符号说明

1.1 “供应商—直播方零售—消费者”模型。“供应商—直播方零售—消费者”模式如图1所示，简称“直播方零售”模式。其中，供应商为主导者。供应商以批发价格ω将商品销售给直播方，直播方再通过直播平台以价格p销售给消费者，消费者的支付意愿应高于商品销售价格，消费者才会选择去购买，设支付意愿为δ，即当δ-p>0时，消费者会选择购买。同时直播方还需向直播平台支付交易费用，单位商品的交易费用为cp。

图1 供应商—直播方零售—消费者模型

则消费者需求函数为：

考虑到在实际情况中，消费者存在退货的行为，因此假设消费者退货函数为R=kq，其中k为商品的退货率，直播方对消费者提供全价退款，由于供应链成员企业能承受的消费者退货率不会超过50%。因此，假设k<0.5。

直播方的利润函数为：

供应商的利润函数为：

1.2 “供应商—直播方代理—消费者”模型。“供应商—直播方代理—消费者”模式如图2所示，简称“直播方代理”模式。其中，供应商为主导者。供货商与直播方签订合同，直播方作为代理商仅为其代销商品且不参与决策，由供应商直接向消费者发货。销售价格由供应商决定，供应商按照商品售价的一定比例向直播方支付佣金，设佣金为ξp，ξ为佣金比例系数，0<ξ<1。供应商还需向直播方支付坑位费用，参考邢鹏等研究，设坑位费为T。由供应商向直播平台支付交易费用，单位商品的交易费用为cp。

图2 供应商—直播方代理—消费者模型

消费者需求函数为：

在该模式下，同样存在消费者退货现象，假设消费者退货函数为R=kq，其中k为商品的退货率，供应商对顾客退货提供全价退款。

供货商的利润函数则为：

直播方的利润函数为：

2 模型决策

2.1 “直播方零售”模式下Stackelberg模型。在分散决策的情形下，该供应链实行供应商主导的Stackelberg博弈，供应商作为主导者，直播方作为跟随者。供应商决定批发价格，直播方决定商品销售价格与服务满意度。通过逆向求解法，对博弈过程中的决策变量均衡解进行计算。

命题1：在此决策方式下，供应链最优决策为：

此时可以求得直播方和供应商在分散决策下的利润分别为：

2.2 “直播方代理”模式下的Stackelberg模型。在分散决策的情形下，该供应链实行供应商主导的Stackelberg博弈，供应商作为主导者，直播方作为跟随者。供应商决定销售价格，直播方决定服务满意度。通过逆向求解法，对博弈过程中的决策变量均衡解进行计算。

命题2：在此决策方式下，供应链最优决策为：

此时可以求得直播方和供应商在分散决策下的利润分别为：

3 均衡解性质分析

针对两种模式下的模型，对上述求得的均衡解进行分析，旨在得到一定的规律和管理启示。

命题3 在“直播方零售”的模式下，商品的最优销售价格、批发价以及直播方的最优服务质量努力程度、供应商和直播方利润均与商品退货率呈负相关。

命题3表明在“直播方零售”的模式下，随着退货率的提高，直播方将通过降低服务成本来弥补退货造成的损失，采取降低商品售价的手段来刺激销量的提升。由于退货率的上升影响着整个供应链的供需情况，处于上游的供应商也因此受到影响，不得不降低批发价格。越高的退货率导致供应商、直播方的利润越低，不利于供应链的良好发展。对此，降低商品的退货率是十分有必要的。导致消费者退货的因素常常与直播方对商品的夸大宣传、商品的品质有关，因此，直播方在讲解商品时应做到实事求是，拒绝虚假宣传、过度宣传，而供应商应严格把控商品的质量，从源头上降低退货的风险。

命题4 在“直播方代理”的模式下，商品的最优销售价格、直播方最优服务质量努力程度、直播方利润均与佣金比例呈正相关，供应商利润与佣金比例呈负相关。

命题4表明在“直播方代理”模式下，当佣金比例增加时，供应商为保证自身利益，会通过提高销售价格来弥补成本的增加。同时也说明供应商愿意花费更多的直播营销成本去提升商品的销量，对直播方的服务质量努力程度有了更高的要求。整体上来说，佣金比例的提升有利于直播方，但会导致供应商利润的下降。所以一般情况下，佣金比例都较低，如在“淘宝”平台上，供应商支付给直播方的佣金比例往往低于20%。因此，直播方主要依靠卖出更多的商品赚取利润。

4 算例分析

为更直观的分析在“直播方零售”模式下，退货率、消费者对直播服务质量努力的敏感系数对均衡解的影响。在“直播方代理”模式下，佣金比例系数、消费者对直播服务质量努力的敏感系数对均衡解的影响。假设“直播方零售”模型中的参数取值如下：d=10，c=0.1；假设“直播方代理”模型中的参数取值如下：d=10，k=0.2，c=0.1，T=1。

4.1 “直播方零售”模式下退货率对均衡解的影响。根据以上的参数赋值和模型假设，取消费者对直播服务质量努力的敏感系数t=0.5，退货率k的取值范围为(0,0.5)，结果如图3、图4所示：

图3 退货率对均衡解的影响

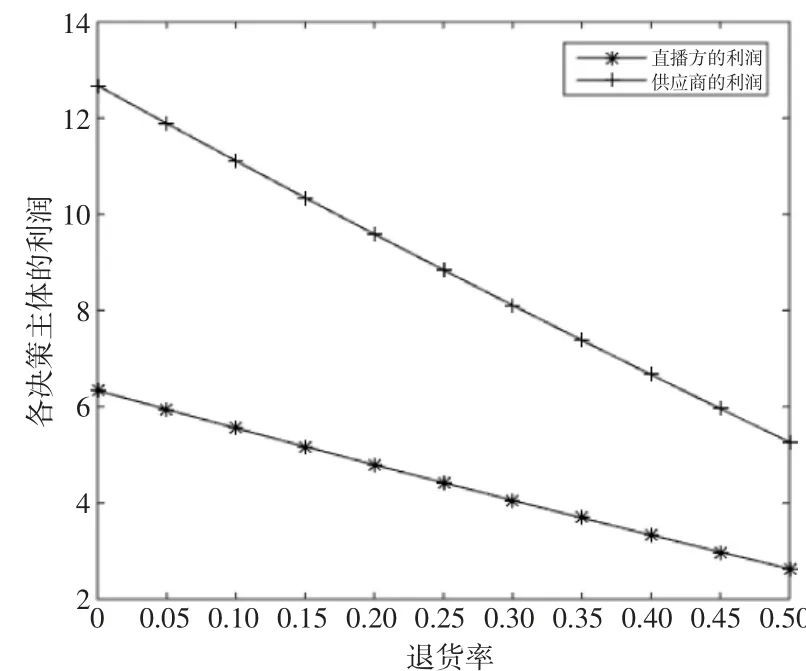
图4 退货率对各主体利润的影响

由图3可知，最优销售价格、批发价格与直播的最优服务质量努力程度均与退货率呈负相关，该结论与命题3一致，由于退货率的提升，直播方的损失进一步扩大，为减小退货带来的损失，直播方不得不降低直播服务的成本，并且通过降低售价来增加商品的销量。由图4可知，直播方、供应商的利润随着退货率的升高而降低，并且退货率对供应商利润造成的影响程度大于对直播方造成的影响程度。因此，为减少过高的退货率造成的损失，供应商需从源头上降低退货的风险，保证自身产品的优质性。直播方应如实宣传商品，降低商品与介绍不符导致的商品退货率。

4.2 “直播方零售”模式下直播服务质量努力的敏感系数对均衡解的影响。根据以上的参数赋值和模型假设，取退货率k=0.2，消费者对直播服务质量努力的敏感系数t的取值范围为(0,0 .6)，结果如图5、图6所示：

图5 敏感系数对均衡解的影响

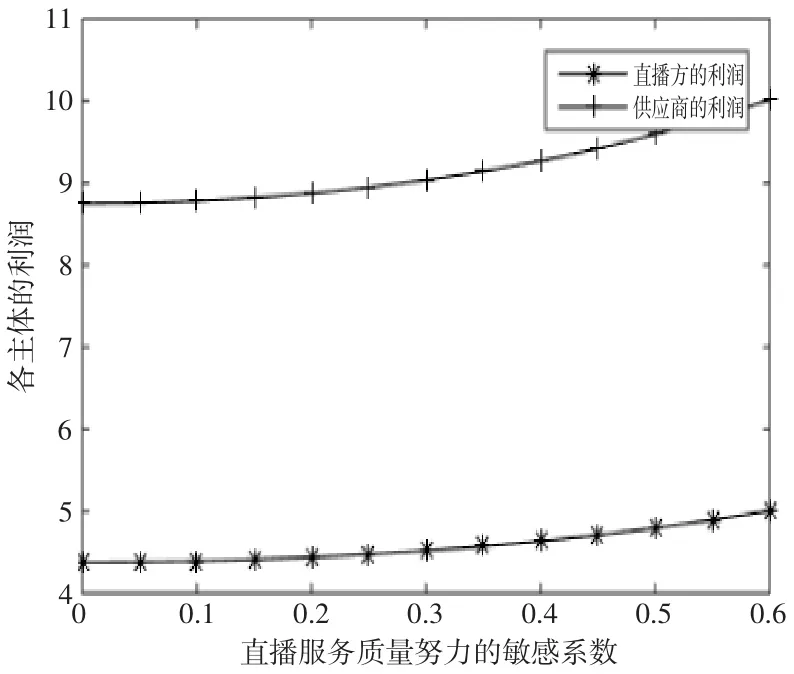
图6 敏感系数对各主体利润的影响

由图5可知最优销售价格、直播的最优服务质量努力程度与消费者对直播服务质量努力的敏感系数呈正比，而批发价不受直播服务质量努力的敏感系数的影响。消费者对直播方的质量努力越敏感，直播方的服务质量努力水平也跟着提升，但直播方的服务成本随之增加。直播方则通过提高商品的售价来增加单个商品的利润，减少成本的增加带来的损失。由图6可知，直播方、供应商的利润随着直播服务质量努力的敏感系数的升高而增加，但直播服务质量努力的敏感系数对供应商利润造成的影响大于对直播方造成的影响，且随着敏感系数的增大，对供应商利润的影响变大。对此，供应商可以采取一些措施提高直播方的服务努力程度来扩大其利润，达到双赢的目的。

4.3 “直播方代理”模式下佣金比例系数对均衡解的影响。根据以上的参数赋值和模型假设，取消费者对直播服务质量努力的敏感系数t=0.5，佣金比例系数ξ的取值范围为(0,0.3)，结果如图7、图8所示：

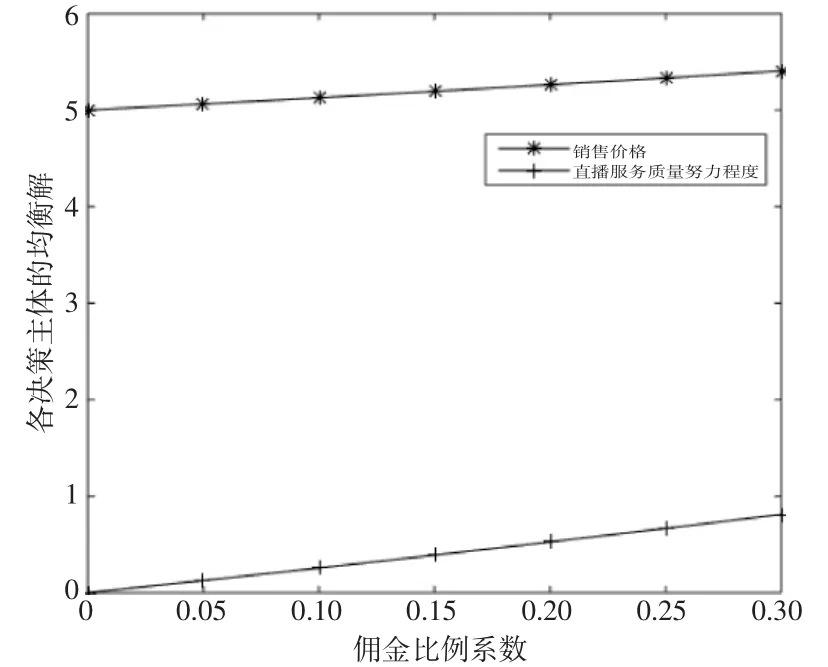
图7 佣金比例系数对均衡解的影响

图8 佣金比例系数对各主体利润的影响

由图7可知，最优销售价格、直播的最优服务质量努力程度均与佣金比例成正比，该结论与命题4一致。佣金比例的提高意味着直播方能获取更多的利润，刺激直播方付出更大的努力提升服务水平。由图8可知，佣金比例的提升虽有利于直播方，但会导致供应商利润的下降，由于该模型下供应商占据主导地位，因此在供应商与直播方商定佣金比例时，供应商更具有话语权。在现实情况中，佣金比例往往低于20%。

4.4 “直播方代理”模式下直播服务质量努力的敏感系数对均衡解的影响。根据以上的参数赋值和模型假设，取佣金比例系数ξ=0.2，消费者对直播服务质量努力的敏感系数t的取值范围为(0,0.6)，结果如图9、图10所示。

由图9可知最优销售价格、直播的最优服务质量努力程度均与直播服务质量努力敏感系数呈正相关。由图10可知，直播方、供应商的利润均与直播服务质量努力敏感系数呈正相关。当消费者对直播服务质量努力的敏感系数的值超过0.35时，对供应商利润的影响程度明显增大。因此供应商与直播方在直播前期，可加大对直播的宣传，让消费者充分了解直播带货下商品的优惠力度，提升消费者对直播服务质量努力的敏感程度。

图9 敏感系数对均衡解的影响

图10 敏感系数对各主体利润的影响

5 结论

本文构建了“供应商—直播方零售—消费者”、“供应商—直播方代理—消费者”两种模式的决策模型，研究直播电商不同的销售模式下，供应商与直播方的最优决策问题，并进一步分析了在“直播方零售”模式下，商品的退货率、消费者对直播服务质量努力的敏感系数对均衡解的影响；在“直播方代理”模式下，佣金比例系数、消费者对直播服务质量努力的敏感系数对均衡解的影响。研究结果表明：（1）在“直播方零售”模式下，最优销售价格、批发价以及直播方的最优服务质量努力程度均与商品退货率呈负相关，直播方、供应商的利润随着退货率的升高而降低。因此为减少过高的退货率造成的损失，供应商需从源头上提高自身产品的质量，降低退货的风险，保证产品的优质性。直播方在讲解商品时应做到实事求是，拒绝过度宣传、虚假宣传。（2）在“直播方零售”模式下，最优销售价格、直播的最优服务质量努力程度与直播服务质量努力的敏感系数呈正比，而批发价不受直播服务质量努力的敏感系数的影响。直播方、供应商的利润随着直播服务质量努力的敏感系数的升高而增加，但直播服务质量努力的敏感系数对供应商利润造成的影响大于对直播方造成的影响，因此，供应商可采取相应措施激励直播方提高服务努力水平来扩大其利润，合作共赢。（3）在“直播方代理”的模式下，商品的最优销售价格、直播方的最优服务质量努力程度和直播方的利润均与佣金比例呈正相关，随着佣金比例的增加，供应商销售价格和直播方服务质量均提高，而供应商的利润却下降。所以在一般情况下，佣金比例都较低，直播方主要依靠提升销量赚取更多利润。（4）在“直播方代理”的模式下，最优销售价格、直播的最优服务质量努力程度均与直播服务质量努力敏感系数呈正相关。直播方、供应商的利润也均与直播服务质量努力敏感系数呈正相关。因此供应商与直播方在直播带货前，可采取网络宣传等手段提升消费者的敏感程度。

本文针对直播电商供应链仅分析了直播方与供应商之间的博弈，还未涉及到原产地、物流、仓储等环节。今后的研究中可引入物流方等其他供应链成员企业，进一步探究直播电商供应链中多方主体间的最优决策问题。