考虑产品绿色度和营销努力的制造供应链成本分担契约研究

刘丙泉 郑湘儒 常旭冉 孟令奇 郝红文

摘要：工业化的迅速发展导致人与自然的矛盾日益突出，绿色产品受到越来越多消费者的青睐，许多制造商和零售商开始生产和营销绿色产品以满足消费者的需求。通过研究制造商和零售商分别为主导的二级绿色制造供应链，采用Stackelberg博弈方法研究需求依赖于产品绿色度和营销努力时的供应链决策与协调问题，提出研发成本和营销成本分担契约。研究发现：（1）制造商和零售商分别为主导时，当研发成本分担系数和营销成本分担系数满足一定的条件范围时，契约供应链将优于无成本分担时的供应链。（2）制造商为主导时，随着研发成本分担契约参数λ的逐渐增大，产品零售价格、产品批发价格、产品绿色度和营销努力水平都呈现出先增后减的趋势。（3）零售商为主导时，随着营销成本分擔契约参数μ逐渐增大，产品零售价格、产品批发价格、产品绿色度都呈现出下降的趋势，而营销努力水平呈现出上升的趋势。最后使用数值仿真，对研究结论和重要参数进行仿真分析。

关键词：产品绿色度;营销努力;Stackelberg博弈;成本分担契约

中图分类号：X322;F426

文献标识码：A

文章编号：1673-5595（2022）02-0090-08

一、引言

伴随着工业化进程的不断加快，全球环境矛盾日益突出、资源浪费问题日益加重、极端突发天气日益增加[1]，对此，消费者的环保意识不断增强，在消费时寻求带有一定绿色度的产品代替普通产品。为了能在激烈的市场竞争中立于不败之地，制造企业积极进行绿色产品研发以提升产品绿色度;零售企业销售绿色产品以满足消费者的环保需求。绿色产品的持续高效发展离不开制造商和零售商的共同努力，双方也都积极探索如何实现绿色产品制造供应链上各自成本收益与环境绩效之间的平衡。成本分担契约是实现这一平衡的重要方式。如产品制造需要付出研发成本时，此时的零售商就对研发成本进行分担，现实中有沃尔玛对其上游供应商投入巨额资金支持其采购新疆有机棉的案例[2];与之类似，零售商营销该产品付出额外的营销成本时，此时的制造商就对营销成本进行分担，现实中有百事可乐通过现金奖励的方式减轻各级零售商销售压力的案例。因此，制造商与零售商如何利用成本分担方式有效地开展协调合作，在满足消费者合理适度的绿色产品市场需求的同时，提升供应链整体效能成为制造企业和零售企业亟需解决的一个关键问题。

近年来，有关产品绿色度的供应链研究是国内外研究的热点问题。有些学者探究不同的假设条件对产品绿色度的影响，如徐乾程等[3]在消费者有效需求的前提下探究有效绿色需求对产品绿色度的影响，并对比探究不同决策情形下的产品绿色度水平，研究表明集中决策下的产品绿色度水平优于制造商主导下的产品绿色度水平。魏光兴等[4]研究偏好异质性及其信息不对称对产品绿色度产生何种影响，研究发现偏好信息不对称会降低产品绿色度，但偏好异质性变化则与产品绿色度成正比。邢光军等[5]研究消费者绿色偏好对产品绿色度及各参与企业利润的影响，研究发现产品绿色度与消费者绿色偏好呈正比，且制造商的利润随着竞争强度的增大而减少，而零售商则反之。罗福周等[6]研究政府补贴策略对产品绿色度以及制造商、零售商利润的影响，研究表明政府合理的补贴范围会提升产品绿色度以及消费者的绿色需求，且制造商和零售商的利润也会随着绿色产品需求的增多而增大。朱琳等[7]进一步将政府补贴拓展到双渠道绿色供应链中，研究也表明政府对绿色产品实施的补贴政策会有效刺激绿色产品的市场需求以及提高制造商和零售商的利润水平。以上研究都是基于制造商为主导时的绿色供应链情形，因此有学者从零售商角度研究绿色供应链，如周岩等[8]研究零售商的公平关切行为对绿色供应链相关决策的影响，研究发现产品绿色度与产品市场需求量以及供应链各主体利润呈正比，且产品绿色度水平越高，制造商使用直销渠道销售产品的利润也越大。

也有学者进一步在绿色供应链中引入契约模型进行协调。有些学者使用单一契约模型对供应链进行协调，如Ghosh等[9]研究成本分担契约如何对供应链中的产品绿色度和收益产生影响，研究表明成本分摊契约能带来更高的产品绿色度和供应链利润。江世英等[10]在制造商和零售商分别主导的情形下构建了考虑产品绿色度的Stackelberg博弈模型，比较分析了产品绿色度并引入收益共享契约协调供应链，研究表明，集中决策下的产品绿色度水平最高，而制造商主导下的供应链产品绿色度水平最低，收益共享契约下的制造商和零售商的利润均高于分散决策下的利润。许格妮等[11]研究了三种不同的绿色成本分担模式对产品绿色度和各供应链节点企业利润的影响，研究表明，成本分担契约适用于制造商研发成本分担比例较大和绿色竞争强度不激烈时的情形。也有学者采用多种契约模型进行对比研究，如张涑贤等[12]研究政府、供应商和零售商所组成的绿色供应链，对比了批发价格契约、收益共享契约和数量折扣契约模型下三个主体偏向于何种契约模型，研究表明，同等产品绿色度下，制造商更倾向于选择批发价格契约，而供应商和政府则更倾向于选择收益共享契约或数量折扣契约。可以看出，引入契约模型能够有效提升产品绿色度和供应链上各参与企业的利润，是提升供应链整体效益的有效方式。

值得注意的是，无论是产品还是服务，如何更好地推广或创新是更值得关注的问题，而营销则是产品或服务推广和创新不可或缺的重要手段，因此也有学者专门研究营销对供应链产品的影响，如鲁芳等[13]探究营销努力和产品体验如何交互影响服务水平，结果表明营销努力与服务水平效应成正比，即营销水平越高，服务水平越高。李新然等[14]研究零售商对再制造品进行销售努力的情况，研究结果显示，零售商的销售努力能显著提升再制造品的市场需求，且零售商若进行合理的销售努力则会有效地提升供应链系统的整体利益。禹海波等[15]研究需求依赖于营销努力水平的供应链问题，结果表明，销售努力水平是否提高受产品需求变化的影响。也有些学者探究营销对绿色产品供应链的影响，如劳可夫[16]指出企业新颖的绿色营销方式会吸引消费者对绿色产品的购买，有利于绿色产品的市场推广。白春光等[17]认为市场需求的扩大和供应链成员的绿色制造决策会受到绿色产品的营销实践影响。刘丛等[18]研究发现营销努力水平的提升有利于推动绿色产品创新。Wang等[19]构建不确定需求下同时受绿色投资和销售努力影响的供应链决策模型，结果表明投资或销售成本系数的增加会降低营销努力和绿色水平，而议价能力越强的主体，其利润水平也越高。

此外，也有学者进一步将契约模型引入与营销相关的供应链中。张廷龙等[20]针对零售商营销努力影响需求的情况，探讨了基于营销努力成本分担的合作机制。赵黎明等[21]探讨合作模式与非合作模式下供应链如何协调低碳产品的营销问题，结果表明相对于非合作情形，合作情形将会提高零售商的营销努力水平，且低碳产品供应链的整体效益均能达到最优。Hong 等[22]发现制造商承担零售商的绿色营销成本会降低零售商的利润水平，但其促进了制造商的绿色设计与生产。Taylor[23]指出当需求受零售商营销努力影响时，销售回扣契约和退货契约相结合的新契约形式可以促使零售商投入最优营销努力。禹海波等[15]使用收益共享契约和数量折扣契约的组合形式对需求依赖于营销努力的供应链进行协调，结果表明，组合的契约形式不仅可以有效协调需求依赖于营销努力的供应链，还能够提升供应链各主体的利润水平。

通过以上文献回顾可以看出：多数学者或探究不同的假设条件对绿色产品的影响，或探究营销努力对供应链产品或服务的影响，然而较少学者同时研究绿色产品和营销努力对市场需求的影响;此外，少数学者虽同时考虑了绿色产品和营销努力[24]，但均假设产品绿色度与研发因子、营销因子间不存在相关性，然而制造商研发因子越大，其所花费的研发成本越高，绿色产品的价格也越高，而这将会降低消费者对绿色产品的偏好，零售商营销因子与之类似，而以往研究未将产品绿色度与这二项因子进行联系;再者，回顾以往的研究，大多数的供应链研究均假设制造商为供应链中的主导者，然而现实中零售商的地位也愈发重要。因此，本文的研究内容如下：（1）探究产品绿色度和营销努力同时影响市场需求时对供应链各主体产生何种影响;（2）考虑产品绿色度与制造商的研发因子、零售商的营销因子具有负相关性;（3）研究制造商和零售商分别在供应链中处于主导地位时的决策情形。基于此，本文首先研究制造商和零售商分别占主导地位时的两阶段绿色产品制造供应链，分析产品绿色度和营销努力对供应链相关决策的影响，并进一步运用成本分担契约对制造商和零售商分别主导时的两阶段绿色产品制造供应链进行协调探究。

二、问题描述与模型假设

考虑单个制造商和零售商组成的二级绿色制造供应链，在此供应链中，制造商为满足消费者对绿色产品的需求，研发设计和生产绿色产品，零售商对绿色产品进行营销，制造商和零售商均为风险中性。本文做出如下假设：

（1）市场需求依赖于零售价格、产品绿色度和零售商营销努力度，即绿色产品的市场需求函数为D=a-p+kg+ns，其中a>0。

（2）基于Ghosh等[9]的研究，假设制造商的研发成本为

12mg2，零售商的营销成本为12vs2，制造商研发因子和零售商营销因子对消费者绿色偏好的影响系数均为x，营销因子对消费者营销努力敏感度为y，设为：k=1xm;k=1xv;n=1yv。

（3）制造商研发成本越高，零售商也需要付出同等的营销成本，即制造商研发因子m等于零售商营销因子v。

（4）零售商为激励制造商提升产品的绿色度，其承担制造商的λ倍（0<λ<1）的研发成本，制造商为激励零售商付出更高的营销努力水平，其承担零售商的μ倍（0<μ<1）的营销成本。模型涉及的主要参数汇总如表1所示。由此可得制造商和零售商的利润函数πm、πr分别为：

πm=（w-c）（a-p+kg+ns）-x2kg2（1）

πr=（p-w）（a-p+kg+ns）-yns2（2）

三、分散决策模式下的博弈模型

（一）制造商主导零售商追随的博弈模型

分散决策下，制造商和零售商以最大化自身利润为目标，双方构成Stackelberg博弈，在以制造商为主导的供应链中，制造商先确定产品的批发价格与绿色度，零售商在此基础上确定产品零售价格和营销努力。制造商和零售商的利润函数为：

πm1=（w1-c）（a-p1+kg1+ns1）-x2kg21（3）

πr1=（p1-w1）（a-p1+kg1+ns1）-yns21  （4）

命题1：制造商的利润函数πm1是关于产品绿色度g1的严格凸函数。当4yn-n2>0时，零售商利润函数πr1是关于零售价p1和营销努力s1的严格凹函数。

证明：因为2πm1g21=-xk<0，所以πm1是关于产品绿色度g1的严格凸函数。又由2πr1p21=-2<0，2πr1s21=-2yn<0，且2πr1p21×2πr1s21-2πr1p1s12πr1s1p1=4yn-n2>0，所以當4yn-n2>0时，πr1是关于零售价p1和营销努力s1的严格凸函数。综上，由命题1可得结论：制造商和零售商利润函数均有最大值。

运用逆向归纳法，由πm1w1=0，πm1g1=0，πr1p1=0，πr1s1=0联立可得，分散决策下的最优决策结果分别为：

w*1=k（n+1-2y）[c（3n-10y）-a（n-2y）]（n-2y）[k（n-2y）（n+1-2y）+3x（4y-n）2]（12y-3n）+2yc-a（n-2y）12y-3n（5）

g*1=（n+1-2y）[c（3n-10y）-a（n-2y）]k（n-2y）（n+1-2y）+3x（4y-n）2（6）

p*1=kg*1（2y-n）2+6y（4y-n）3（4y-n）2+a（2y-n）2+2yc（2y-n）3（4y-n）2+2ya4y-n（7）

s*1=a4y-n-c（n+1-2y）x（4y-n）2+k（n+1-2y）-x（4y-n）x（4y-n）2w*1（8）

最优利润分别为：

πm1=（w*1-c）（a-p1+kg*1+ns*1）-x2kg*1 2（9）

πr1=（p1-w*1）（a-p1+kg*1+ns*1）-yns*1 2（10）

（二）零售商主导制造商追随的博弈模型

与上节一致，本小节仍然在供应链分散决策的情形下，在以零售商为主导的供应链中，零售商先确定零售价格和营销努力，制造商在此基础上确定产品的批发价格和产品绿色度。此时制造商和零售商的利润函数分别为：

πm2=w2（a-p2+kg2+ns2）-12mg22（11）

πr2=（p2-w2）（a-p2+kg2+ns2）-12vs22（12）

命题2：与上节结论一致，零售商为主导时的制造商的利润函数πm2是产品绿色度g2的严格凸函数。当4yn-n2>0时，零售商的利润函数πr2是关于产品零售价p2和产品营销努力s2的严格凸函数。

证明：因为2πm2g22=-xk<0，所以πm2是关于产品绿色度g2的严格凸函数。又由2πr2p22=-2<0，2πr2s22=-2yn<0，且2πr2p22×2πr2s22-2πr2p2s22πr2s2p2=4yn-n2>0，所以当4yn-n2>0时，πr2是关于零售价p2和营销努力s2的严格凸函数。综上，由命题2可得结论：制造商和零售商利润函数均有最大值。

运用逆向归纳法，由πm2w2=0，πm2g2=0，πr2p2=0，πr2s2=0联立可得，零售商主导下的分散决策下的最优决策结果分别为：

w*2=xk3axy-c（nx+ky）3y（x-k）+nc3y-a+c

（13）

g*2=1k3axy-c（nx+ky）3y（x-k）+nc3y-a（14）

p*2=3axy-c（nx+ky）3y（x-k）（15）

s*2=c3y（16）

最优利润分别为：

πm2=（w*2-c）（a-p*2+kg*2+ns*2）-x2kg*2 2（17）

πr2=（p*2-w*2）（a-p*2+kg*2+ns*2）-yns*2 2（18）

四、分散决策模式下的成本分担契约模型

（一）制造商主导下的研发成本分担契约

考虑到制造商设计生产绿色产品需要付出大量的研发制造成本，为确保制造商对绿色产品的持续研发投入，提升研发效率，本小节在以制造商为主导者零售商为追随者的供应链中，设计零售商对制造商的绿色产品研发成本进行分担，形成研发成本分担契约。下面对该契约的协调性进行分析，此时研发成本分担比例为λ，产品零售价格为p3

，绿色度为g3，批发价格为w3，营销努力为s3。制造商和零售商的利润函数分别为：

πm3=（w3-c）（a-p3+kg3+ns3）-x2kg23  （19）

πr3=（p3-w3）（a-p3+kg3+ns3）-yns23  （20）

采用逆序计算法求解零售商的利润函数可得：

p*3=2y（3a+1）-n（a+1）2（4y-n）+

4ky（a+1-2c）x（4y-n）（1-λ）-4ky×k（6y-n）2（4y-n）（21）

g*3=4y（a+1-2c）x（4y-n）（1-λ）-4ky（22）

w*3=a+12+2ky（a+1-2c）x（4y-n）（1-λ）-4ky（23）

s*3=a-18y-2n+4ky（8y-2n）（a+1-2c）x（4y-n）（1-λ）-4ky（24）

将p*3 、g*3 、w*3 、s*3 代入制造商的利润函数可得：

πm3=（w*3-c）（a-p*3+kg*3+ns*3）-x2kg*3 2（25）

πr3=（p*3-w*3）（a-p*3+kg*3+ns*3）-yns*3 2（26）

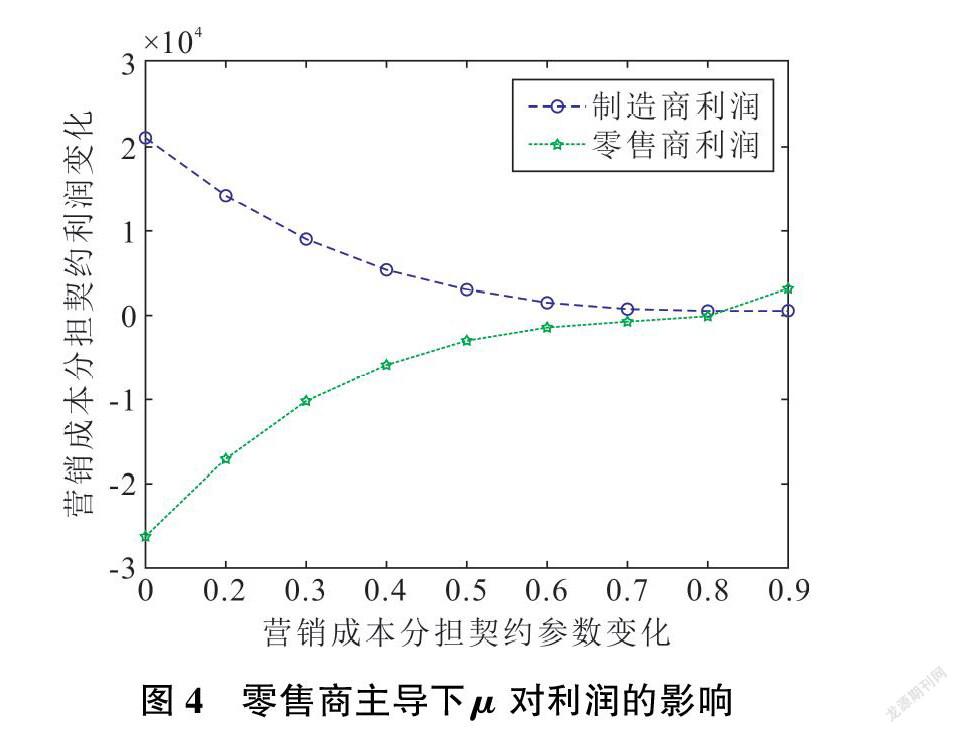
命题3：当1-4y（a+1-2c）[k（n-2y）（n+1-2y）+3x（4y-n）2]x（4y-n）（n+1-2y）[c（3n-10y）-a（n-2y）]+4kyx（4y-n）<λ<1时，制造商主导下的研发成本分担契约优于无契约下的最优决策。

证明：若使制造商主导下的研发成本分担契约供应链决策优于无成本分担下的供应链决策，此时的最优决策应满足：产品绿色度g*1

λ>1-4y（a+1-2c）[k（n-2y）（n+1-2y）+3x（4y-n）2]x（4y-n）（n+1-2y）[c（3n-10y）-a（n-2y）]+4kyx（4y-n），又由于0<λ<1，所以命题得证。由命题3可得结论：当研发成本分担比例满足命题3范围时，制造商主导下的研发成本分担契约供应链决策将优于无成本分担下的供应链决策，制造商主导的此种情况下，制造商和零售商都能够获得最大利润，消费者也能购买到高绿色度的环保产品，双方达到互利共赢的效果。

（二）零售商主导下的营销成本分担契约

考虑到零售商营销绿色产品需要付出营销成本，因此，为激励零售商付出更高水平的营销努力，本小节在零售商主导下的分散决策情形下，考虑制造商分担零售商对绿色产品的营销努力成本，形成营销成本分担契约。下面对该契约的协调性进行分析，此时成本分担比例为

μ，产品零售价格为p4，绿色度为g4，批发价格为w4，营销努力为s4。制造商和零售商的利润函数分别为：

πm4=（w4-c4）（a-p4+kg4+ns4）-x2kg24-μns24  （27）

πr4=（p4-w4）（a-p4+kg4+ns4）-（1-μ）yns24  （28）

采用逆序计算法对制造商的利润函数进行求解可得：

p*4=[4ky（1-μ）-nx][c（2kx-x-4k2）+a]+n（ax-kc）（2k-x）[4ky（1-μ）-nx]-n（k-x）（29）

s*4=p*4 （k-x）+ax-kc4ky（1-μ）-nx（30）

g*4=p*4×12k-n（k-x）2k[4ky（1-μ）-nx]+

n（ax-kc）2k[4ky（1-μ）-nx]-a2k-cx（31）

w*4=xp*4×12k-n（k-x）2k[4ky（1-μ）-nx]+

n（ax-kc）2k[4ky（1-μ）-nx]-a2k+c（32）

将p*4、s*4、g*4、w*4代入制造商和零售商的利润函数得：

πm4=（w*4-c）（a-p*4+kg*4+ns*4）-x2kg*4 2（33）

πr4=（p*4-w*4）（a-p*4+kg*4+ns*4）-yns*4 2（34）

命题4：当

1-n（k-x）[3axy-c（nx+ky）]12ky2（x-k）[c（2kx-x-4k2）+a+n（ax-kc）]+nx4ky<μ<1

时，零售商主导下的营销成本分担契约优于无契约下的最优决策。

证明：零售商主导下的营销成本分担契约供应链决策若想优于无成本分担下的供应链决策，那么此时的最优决策应满足：产品绿色度g*2 1-n（k-x）[3axy-c（nx+ky）]12ky2（x-k）[c（2kx-x-4k2）+a+n（ax-kc）]+nx4ky，又由于0<μ<1，所以命题得证。由命题4可得结论：当营销成本分担比例满足命题4的范围时，零售商主导下的营销成本分担契约供应链决策将优于无成本分担下的供应链决策，零售商主导的此种情况下，制造商和零售商都能够获得最大利润，消费者也能购买到高绿色度的环保产品，双方达到互利共赢的效果。

五、数值分析

为验证所提出的模型的正确性，使用MATLAB软件对上述模型进行数值仿真。模型中参数赋值如下：a=10，k=1，n=1，x=2，y=2，c=1。

图1反映制造商主导下的契约参数λ对供应链最优决策变化的影响。从图1可以看出，随着λ逐渐增大，产品零售价格、产品批发价格、产品绿色度和营销努力水平都呈现出先增后减的趋势。这是因为：当研发成本分担比例λ不断增大时，制造商由于零售商对其绿色产品研发成本进行一定的分担，其绿色产品研发资金较独立情形下更加充裕，这会激励制造商加大产品的绿色研发投入，由此带来产品绿色度水平提升的同时也会提高绿色产品的批发价格。与此同时，零售商由于分担制造商一定的绿色产品研发成本，直接加大了自身的成本压力，在承担绿色产品的营销成本基础上也承担了绿色产品的研发成本，其只能通过提高绿色产品价格的方式来缓解成本压力。而零售商通过参与到制造商研发绿色产品的过程中，自身对营销绿色产品的动力也会增强，其营销努力水平也会依据研发分摊的比例的变化而变化。值得注意的是，随着分担比例λ的逐渐增大，制造商和零售商都需承担更大的成本压力，其产品零售价格、产品批发价格、产品绿色度和营销努力水平都会逐渐降低，表明研发成本分担比例λ在合理的范围内才是有利的。

图2反映零售商主导下的契约参数μ对供应链最优决策变化的影响。从图2可以看出，随着契约参数μ逐渐变大，产品零售价格、产品批发价格、产品绿色度都呈现出

下降的趋势，而营销努力水平则呈现出上升的趋势。这是因为：零售商为主导时，当营销成本分担比例μ不断增大时，制造商对零售商的营销成本分担会激励零售商的营销积极性，其对绿色产品的营销努力水平也会有所提升，而产品的零售价格则由于营销成本压力减轻而降低。但对于制造商而言，为维持其成本投入保持在一定范围内，其会通过削减其绿色产品研发资金投入的方式以分担零售商的营销成本，产品绿色度会因研发资金投入的减少而降低，进而导致批发价格降低。

图3和图4反映制造商和零售商分别主导下的契约参数λ和μ对供应链利润的影响。从图3可以看出，随着契约参数λ的逐渐变大，制造商利润在不断增加，而零售商利润在不断减少。从图4可以看出，随着契约参数μ的逐渐变大，制造商利润在不断减少，而零售商利润在不断增加，但二者利润都要比契约分担前的分散决策

图4 零售商主导下μ对利润的影响状态下的利润水平要高。因此可以认为，成本共担契约能够协调此类型的供应链。这是因为：当零售商对制造商的研发成本进行分担时，其减轻了制造商在绿色产品研发投入上的资金压力，其分担产品研发成本比例越大，其利润水平也会逐渐降低，而制造商的利润水平变化则相反，即零售商分担研发成本越多，制造商的利润越高。而当制造商对零售商的营销成本进行分担时，其会缓解零售商在绿色产品营销成本投入上的资金压力，但分担产品营销成本比例越大，其利润也会逐渐降低，而零售商的利润水平则与其相反，即制造商分担营销成本越多，零售商的利润越高。在满足分担比例范围内，制造商与零售商具体的分担比例为多少有赖于双方议价能力的高低，这与多数学者的研究具有一致性。

六、结论与建议

本文研究制造商和零售商分别占主导地位时的两级绿色制造供应链，在产品绿色度和营销努力共同影响需求的情况下，采用Stackelberg博弈探究产品绿色度和营销努力对绿色制造供应链决策的影响。在制造商为主导企业时，运用研发成本分担契约对绿色制造供应链进行协调探究;在零售商为主导企业时，运用营销成本分担契约对绿色制造供应链进行协调探究。研究表明：（1）当制造商为主导时，零售商对制造商的研发成本分担需要满足一定的条件，此时，随着研发成本分担契约参数λ的逐渐增大，制造商主导下的供应链的产品零售价格、产品批发价格、产品绿色度和营销努力水平都呈現出先增后减的趋势;（2）当零售商为主导时，制造商对零售商的营销成本分担也需满足一定的条件，此时，随着营销成本分担契约参数μ逐渐增大，零售商主导下的产品零售价格、产品批发价格、产品绿色度都呈现出下降的趋势，而营销努力水平呈现出上升的趋势。可以认为，契约分担下的制造商和零售商的利润都优于无契约时分散决策下的情形。因此，在以制造商和零售商分别为主导的绿色制造供应链中，成本分担契约可以达到绿色制造供应链上双方互利共赢的效果。

根据研究结论，提出如下建议：（1）当制造商为主导时，制造商拥有供应链的主导权，制造商可基于文章中的研发成本分担契约模型设计合理的研发成本分担比例，即零售商分担制造商的研发成本，以此种方式可以减轻自身的研发资金压力，提升产品的绿色度水平;（2）当零售商为主导时，零售商掌握供应链的主导权，零售商可基于文章中的营销成本分担契约设计合理的营销成本分担比例，即制造商分担零售商的营销成本，以此方式减轻零售商自身的营销成本压力，激励零售商提升自身的营销水平，以期实现双方互赢。

参考文献：

[1] 纪玉俊，李志婷.制造业集聚影响城市绿色全要素生产率的门槛效应[J].中国石油大学学报（社会科学版），2020，36（1）：25.

[2] Plambeck E L， Denend L. The Greening of Wal-Mart s Supply Chain Revisited[J]. Supply Chain Management， 2011，15（5）：16-23.

[3] 徐乾程，钱存华.消费者有效需求下的绿色供应链博弈模型研究[J].生态经济，2018，34（1）：74-77.

[4] 魏光兴，付巧玲，陈曦.考虑偏好异质性及其信息不对称的绿色供应链决策[J].软科学，2020，34（11）：123-129.

[5] 邢光军，李云云.考虑消费者绿色偏好的竞争性闭环供应链生产决策研究[J].工业工程，2020，23（5）：22-29.

[6] 罗福周，王文心.考虑产品绿色度的闭环供应链政府补贴策略研究[J].工业工程，2020，23（6）：18-27.

[7] 朱琳，窦祥胜.考虑风险态度的绿色供应链定价策略及政府补贴政策分析[J].工业工程，2020，23（5）：158-168.

[8] 周岩，胡劲松，刘京.考虑公平关切的双渠道绿色供应链决策分析[J].工業工程与管理，2020，25（1）：9-19.

[9] Ghosh D， J Shah. Supply Chain Analysis under Green Sensitive Consumer Demand and Cost Sharing Contract[J]. International Journal of Production Economics， 2015，164：319-329.

[10] 江世英，李随成.考虑产品绿色度的绿色供应链博弈模型及收益共享契约[J].中国管理科学，2015，23（6）：169-176.

[11] 许格妮，陈惠汝，武晓莉，等.竞争供应链中绿色成本分担博弈分析[J].系统工程学报，2020，35（2）：244-256.

[12] 张涑贤，李兰，王少峰.考虑政府补贴的绿色供应链契约分析及优化研究[J].物流科技，2021，44（2）：143-150.

[13] 鲁芳，吴健，罗定提.考虑产品体验性和营销努力的分销渠道合作策略研究[J].中国管理科学，2020，28（10）：144-155.

[14] 李新然，王奇琦.政府补贴下考虑销售努力的闭环供应链研究[J].科研管理，2017，38（8）：51-63.

[15] 禹海波，付建，李健，等.需求可变性和风险偏好对需求依赖促销努力供应链的影响[J].管理工程学报，2021，35（4）：202-215.

[16] 劳可夫.消费者创新性对绿色消费行为的影响机制研究[J].南开管理评论，2013，16（4）：106-113.

[17] 白春光，唐家福.制造-销售企业绿色供应链合作博弈分析[J].系统工程学报，2017，32（6）：818-828.

[18] 刘丛，黄卫来，郑本荣，等.考虑营销努力和创新能力的制造商激励供应商创新决策研究[J].系统工程理论与实践，2017，37（12）：3040-3051.

[19] Wang L， Song Q. Pricing Policies for Dual-Channel Supply Chain with Green Investment and Sales Effort under Uncertain Demand[J]. Mathematics and Computers in Simulation， 2020： 79-93.

[20] 张廷龙，梁樑.不同渠道权力结构和信息结构下供应链定价和销售努力决策[J].中国管理科学，2012，20（2）：68-77.

[21] 赵黎明，孙健慧，张海波.基于微分对策的低碳产品供应链营销合作协调机制[J].管理工程学报，2018，32（3）：105-111.

[22] Hong Z， Guo X. Green Product Supply Chain Contracts Considering Environmental Responsibilities[J].Omega，2019，83（3）：155-166.

[23] Taylor T A.Supply Chain Coordination under Channel Rebates with Sales Effort Effects[J].Management Science，2002，48（8）：992-1007.

[24] 吴正祥，李宝库.利他偏好下需求依赖于价格和营销努力的两级供应链决策与协调[J].中央财经大学学报，2017（12）：108-118.

责任编辑：陈可阔

Research on Supply Chain Cost Sharing Contract Considering Green Product Level and Marketing Efforts

LIU Bingquan1，ZHENG Xiangru1，CHANG Xuran1，MENG Lingqi1，HAO Hongwen2

（1.School of Economics and Management， China university of petroleum （east China）， Qingdao 266580， Shandong， China;

2.Energy security dispatching center of Shandong， Jinan 250014， Shandong China）

Abstract： The article explores the secondary green manufacturing supply chain led by manufacturers and retailers， focusing on the supply chain decision-making and coordination issues entailed by the demand for green product levels and marketing endeavors with the aid of Stackelberg game method and proposes the R&D cost and marketing cost sharing contracts respectively. The study found that： （1）the contract-bound supply chain outperforms the costcharing-free one when led by the manufacturers and retailers， the R&D cost sharing coefficient and marketing cost sharing coefficient meet certain conditions. （2）the product retail and wholesale price， the green levels and the marketing endeavors show trends of increasing initially， followed by decreasing when guided by the manufacturer， the R&D cost sharing contract parameter λ is on gradual increase. （3） the product retail and wholesale price， the green levels show signs of a downward trend with the marketing endeavors on the increase when directed by the retailer， the marketing cost sharing contract parameter μ is on an incremental rise. Finally， the numerical simulation is applied to verify the conclusions and important parameters of this article.

Key words： green product levels; marketing endeavors; Stackelberg game; cost-sharing contract