数学文化与中考试卷融合途径分析

2022-05-13李欣斯琴其木格

赤峰学院学报·自然科学版 2022年4期

李欣　斯琴其木格

摘要：有关数学文化的课题是教育界的研究热点，数学文化背景题已成为各阶段考试的重要考点。本文在分析某省2014-2021年中考数学试卷的基础上，总结数学文化在中考试卷中的分布特点和试卷中融合数学文化的主要途径，为初中数学课程中数学文化相关内容的教与学提供参考。

关键词：数学文化;中考试卷;试卷分析

中图分类号：G642 文献标识码：A 文章编号：1673-260X（2022）04-0068-04

1 引言

《义务教育数学课程标准（2011年版）》中提出：“数学是人类文化的重要组成部分，数学素养是现代社会每一个公民应该具备的基本素养[1]。”《普通高中数学课程标准（2017年版）》中对数学文化的定义是“数学的思想、方法、精神、观点、语言及它们的形成与发展，并且包含数学在人类生活、社会发展、科学技术中的贡献与意义、与数学有关的人文活动[2]。”无论从国家教育部门制定数学课程标准的基本理念角度，还是从相关领域专家学者们提出的观点的角度，均可看出教育界对数学文化的重要性给予了极大的肯定。

自从实施《义务教育数学课程标准（2011年版）》后，各学校在数学课程教学中，充分强调学生全面发展，强调通过数学教育给学生传授数学知识与技能的同时，更要强化数学在培养人的创新能力和思维能力方面作用的发挥。在此背景下，以《课程标准》为主线的中考试卷中出现数学文化背景题的频次逐年上升，内容逐渐增多，形式更加丰富。这种以评价的方式促进教师和学生对数学文化的重视程度，提高学生对数学文化的兴趣，开阔学生文化视野，提高学生文化素养是可行而有效的策略。

本文在对某省2014-2021年（以下简称近8年）中考数学试卷进行分析的基础上，总结试卷中数学文化背景题的概貌，分析中考试卷中融合数学文化的主要途径，为初中数学课程中的数学文化相关内容的教学提供参考。

2 数学文化背景题概貌分析

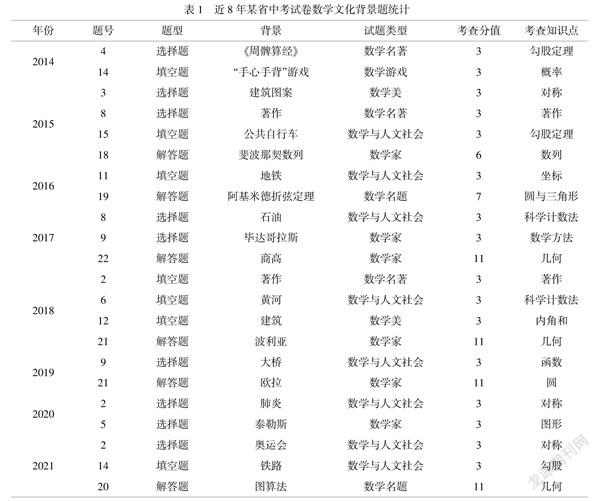
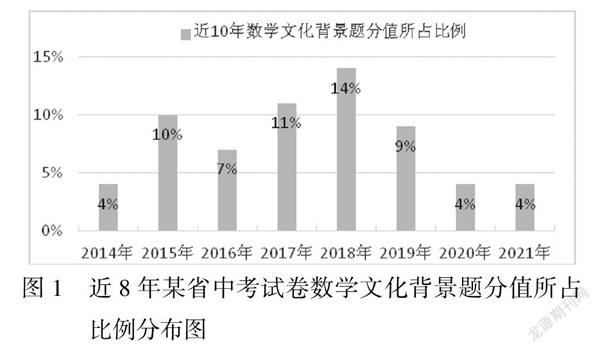
数学文化的定义选取广义的理解，并且结合张维忠、王建磐等人的观点，依据不同的文化载体形式，将中考数学试题中的数学文化类型分为6类，即数学名题、数学名著、数学家、数学美、数学游戏以及数学与人文社会。本文选取某省2014-2021年中考数学试卷为研究对象，从题号、题型、背景、试题类型、考查分值以及考查知识点等方面进行了详细分析。表1为某省近8年中考试卷数学文化背景题的分布特点，图1为近8年中考试卷中数学文化背景题分值占总分值比例，以此来更加清晰直观地总结试卷中数学文化背景题的概貌。

2.1 试题数量特征

以数学文化为背景的中考试题共21道，其中在2015年和2018年出现的这类题目最多，达到了每年4道题。其余几年里相对2015年和2018年而言数学文化相关试题出现的较少，平均每年2-3道。而2012年和2013年还没出现以数学文化为背景的试题。自从2011年《九年义务教育数学课程标准》正式颁布后，在教学评价体系中已经综合考虑了培养数学文化素养目标的达成，数学文化在数学教学中越来越受到重视。从宏观的角度来看，以数学文化为背景的试题成为中考试卷的“常驻嘉宾”，受中考命题者的青睐。

2.2 试题题型特征

以选择题的形式进行数学文化知识的考查居多，共9道，占近8年数学文化背景题总数的43%;其次是填空题，共7道，占33%;再者是解答题，总共5道，占24%。目前中考数学试卷的题型只有选择题、填空题和解答题三大类。而数学文化背景题的考查形式已覆盖了这三大类。其中以选择题为主，几乎在近8年的试卷中每年都会有一道选择题，填空题和解答题也有出现，这更加说明了目前数学文化素养培养方式的多样化和涉及的知识面广度的提高。

2.3 试题类型特征

以数学与人文社会为背景的试题数最多，共8道;以数学家为背景的试题，共6道;以数学名著为背景的试题3道;以数学美为背景的试题2道;以数学名题和数学游戏为背景的试题各1道，并且不同类型题的分值3至11分不等。不难看出，中考命题专家们很注重学生了解社会生活和数学的联系，注重学生对数学来源于生活和生活中处处有数学的理解。对于数学名著的考查，基本涉及《几何原本》《周髀算经》《九章算术》等著作中的数学思想方法等。而在数学美方面，大多数与生活中的某些建筑有关，意在对建筑的几何形式和特征的观察中让学生发现数学之美。其余类型题没有规律可循。

2.4 試题分值特征

如图1所示，数学文化为背景的解答题分值在7-11分，总体上在当年试卷中所占分值比例较大;试卷中以数学文化为背景的选择题、填空题分值比例则较小。从出现规律上看，选择题几乎每年都出现，填空题也大概率会有，但是解答题是否出现在试卷中则没有规律可言。总之，从分析结果可以看出命题专家以评价的方式促进教师教学中渗透数学文化的意图所在，能够从教学评价的角度督促教师增强数学文化背景内容的教学力度，提高学生学习数学文化知识的积极性和主动性。

2.5 考查知识点特征

考查的内容基本都属于图形与几何、数与代数、概率统计这三大领域，涉及函数、圆与三角形、内角和、科学计数法、勾股定理、对称性、概率等知识点。而科学计数法和对称性这两个知识点多数以选择题的形式出现，其余的知识点几乎都在解答题和选择题中出现。其中勾股定理和概率出现在填空题里的概率较大，除了选择题的考查知识点有一定的规律性，其他题型的考查内容没发现任何规律。说明数学文化的内容非常丰富，可以考查多个知识点，涉及多个领域，从侧面反映了数学教学中不断丰富学生的视野至关重要。

综上所述，该省中考试卷通过不同类型的考查，要达到促使学生掌握数学文化基本知识的目的。近8年，在评价中出现数学文化相关问题的次数逐年增多，而这种热度不只是短暂的潮流，且具有持续性。可见在教学中融入数学文化、强化数学文化知识的传授是教师教学非常重要的任务，必须充分考虑教学设计、教材引申、开设趣味课堂等过程中，全方位渗透数学文化。

3 试卷中融合数学文化在教学中的作用

3.1 让学生领悟中华文化的博大精深

纵观我国浩瀚的数学发展史，不仅包括数学的理论研究，还涉及政治、历史、宗教等领域。例如垂径定理的由来、数学发展史的几次危机等，其包含的数学文化元素极其丰富，体现中国文化的多样性。通过试卷让学生了解中国数学史，领会中华文化的博大精深是最常见的呈现形式。

在样本试卷中，2017年试卷第22题是一道以勾股定理为背景的数学文化相关题[3]。勾股定理是常用的重要定理，在教学中要求学生熟记于心的同时更要强调发现此定理的历史背景。西周开国时候，商高回答周公问题时提出了勾股定理，又叫“商高定理”。虽然国外把这个定理叫作“毕达哥拉斯定理”，事实上，古希腊数学家毕达哥拉斯比商高晚生六百多年[4]。勾股定理的发现是我国数学家商高对数学发展做出的突出贡献，是他最早独立提出的。通过这种背景题，能够让学生深入了解中国数学在数学发展中的重要地位，增强学生对数学史的学习动力，更能够激起青年学生的民族自豪感和家国情怀。

3.2 使学生发现数学之美

现在我们国家注重人的全面发展，也就是德智体美劳共同发展，其中所说的美，指的正是人的审美观。在数学课程中培养审美观也是美育的重要组成部分。哪里有数学，哪里就有美[5]！古希腊数学家普洛克拉斯对数学之美给予了如此高的评价。数学中的美，无处不在。如轴对称、中心对称的对称之美，黄金分割的比例之美，勾股定理的简洁之美，具备统一美的各种公式，还有奇异美、自然美、和谐美等。数学之美也体现在日常生活中，如艺术品、广告设计、生活日用品等都会与数学美相关。

在样本试卷中，2014年试卷题第3题是一道选择题，侧重训练学生发现生活中数学之美的能力;2015年试卷题第3题是一道选择题，考查学生用数学的眼光观察数学美的能力[3]。这两道题有个共性，都提到了当地传统建筑特色，呈现当地的传统文化元素。考试题中提到的晋商大院，很多考生可能都去过，但是否观察过这些建筑窗格图案的美感不同之处，是否与数学问题联想到一起等问题也会引起学生对当地传统建筑的关注与喜爱，激发学生对中国古建筑的兴趣。以往可能单纯地欣赏了建筑的整体外观，而日后在观光各地建筑的过程中也会联想到数学相关图形。比如，圆弧形的赵州桥、莫比乌斯环形的北京国际传媒中心、与数列相关的太原双塔、小蛮腰的单叶双曲面等等，数学之美呈现在建筑的每一个细节里。通过试卷可以体现数学的美学价值，让学生领略各地特色建筑之美。

3.3 让学生体会我国数学家和数学著作的魅力

可以用符号和文字精确叙述是数学的文学魅力。正因为古代数学家将数学的发现历程准确地记录并留存下来，后人才有机会学习和研究这些成果。《周髀算经》《九章算术》《考工记》《数书九章》《孙子算经》等都是中国古代数学著作。通过对数学著作的了解，学生会发现这些成果来之不易，即使在科技不发达的古代，数学家依然有许多新发现和新成果。通过试卷让学生领会数学家的数学精神和数学思想。

在样本试卷中，2014年试卷第4题，2015年试卷第8题，2018年试卷第2题都是以数学著作为背景的题目[3]。这种类型题重点考查学生对数学著作的了解程度，考查学生对我国哪些经典数学著作有所了解。而学生对古典数学著作的相关认知几乎都来自历史课或其他途径获得的碎片记忆。在数学教学中应该向学生介绍一些中国的经典数学著作，鼓励学生静下心来读一读这些著作，了解中国数学发展史，用数学家当时的思维方式再次感受这些数学法则和规律的发现过程，体会数学家取得的成就来之不易。这样有助于增强学生对民族文化的自信心，有助于提高学生数学学科素养。

3.4 了解世界数学发展史，领略数学思想的多样化

因文化的差异创造了新的文化。不能仅仅局限于了解中华文化，还要放眼注视多元的世界文化，数学文化也是如此。丰富的数学文化是人类文化共同拥有的宝贵财富，是人类文化不可或缺的一部分。了解世界著名数学家，了解诸多数学成果的发现过程，了解世界上广泛应用的富有影响力的经典数学著作等十分必要。在教学中应该让学生通过多种途径、抓住机会领略世界数学发展史及其数学思想。

在样本试卷中，2017年试卷第9题，2015年试卷第18题，2020年试卷第5题都是以外国数学家证明某些定理为背景的题目[5]。题中出现了毕达哥拉斯、泰勒斯的定理，还提到了有趣的斐波那契数列。这种关注世界数学名家的题目激发学生对科学家的敬仰，增强学生的求知欲。通过试卷给学生更多的学习和了解机会，吸引学生对世界数学文化的关注。

3.5 让学生领略数学的应用价值

除了知识和技能以外，学习丰富的数学文化能够让学生树立正确的数学观，养成用数学的眼光观察世界，能够引起学生数学思考，帮助学生用数学方法解决生活中的实际问题。在教学中，带领学生多动手，通过各种活动形式让学生提高生活中运用数学知识的能力。

在样本试卷中，2014年试卷第9题是一道填空题，是以“手心手背”的游戏为背景的题目，通过一次“手心手背”游戏决定某一方能打乒乓球的概率值[3]。“手心手背”游戏是学生最熟悉不过的，但是學生可能联想不到居然可以用这种方式把数学和游戏结合在一起，用数学知识赢得游戏胜利。这种与学生生活息息相关的数学问题，能够提高学生数学应用意识。

4 结语

随着数学文化研究的热度越来越高，数学文化与中考试卷的融合也逐渐被强化，体现教学评价体系中目标的多元化。关注学生知识水平的同时，关注学生数学文化素养的培养，从而达到培养学生对数学的兴趣，感受中华文化，了解世界文化，提升思维能力，传播数学探究精神等多方面的教学目标。

数学文化在教材、课堂、教学评价中的渗透，必然有力推动学生“认识数学的科学价值、应用价值、文化价值和审美价值”[2]这一数学课程目标的达成。

——————————

参考文献：

〔1〕中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

〔2〕中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

〔3〕某省2012-2021年中考数学试卷.

〔4〕周金才，梁兮.数学的过去、现在和未来[M].北京：中国青年出版社，1982.

〔5〕余廷忠.哪里有数学，哪里就有美——试谈数学的审美教育[J].毕节师专学报，1995，13（01）：70-72+76.

收稿日期：2022-01-25

通讯作者：斯琴其木格（1965-），女，蒙古族，内蒙古赤峰市人，硕士研究生导师，教授，研究方向：数学学科教学，图论。