新旧教材立体几何部分例习题比较研究

●吕海濛 韩 红

一、问题的提出

高中数学的立体几何部分由于比较抽象，难以理解，一直以来都困扰着广大师生。2019 年黑龙江省逐渐普及《2019 版普通高中教科书数学（A 版）》，那么新的问题也就随之而来，作为高中数学的教学重点内容，立体几何部分的例习题数量与类型有哪些变动？例习题的难度是否增加？例习题的教学又该做出那些调整呢？

二、研究对象

本文节选的内容是2019 年6 月人民教育出版社出版的《普通高中教科书数学必修第二册（A 版）》（以下简称“新教材”）中第八章立体几何初步与2007 年2 月人民教育出版社出版的《普通高中课程标准实验教科书数学必修二（A 版）》（以下简称“旧教材”）中第一章空间几何体和第二章点、直线、平面之间位置关系。

三、例习题数量比较

例习题是数学教材中必不可少的内容，无论是完成教学目标，还是培养学生的学科核心素养，都需要一定数量的例习题。本文统计的是教材中明确带有蓝色“例”字标记的例题，立体几何部分的所有练习题、习题，以及复习题，其中若存在一道题含有多个小题的情况时，我们规定，如果每个小题之间是相互独立的，按照小题的数量计算例习题的个数，若各小题之间是相互联系的，则按照一道大题来计算。

经统计，新教材中例题26 道，练习题87 道，习题96 道，复习题17 道，共计226 道例习题；旧教材中例题21 道，练习题61 道，习题81 道，复习题33 道，共计196 道练习题。可以发现，立体几何部分，新旧教材在例习题的数量上有着明显的差距，我们从下面两个方面分析：

（一）新旧教材例习题的数量比较

新教材中例习题共计226 道，旧教材中例习题共计196道，可见，新教材在例习题的总体数量上有所上升，我们具体来看，新旧教材在例题数量上没有发生太大的变化，但在练习题和习题的数量上有所增加，主要是因为新教材在每一小节都配有3～4 个练习题，这样的设置使得学生能够即学即练，能够达到及时巩固知识的目的。在复习题方面，旧教材将立体几何部分设置为两个章节，故含有两个章末复习题，而新教材只有一个复习题，因此在复习题的数量上新教材要少于旧教材。值得一提的是，在第二小节中，新教材删除了“立体几何三视图”部分内容，主要是由于在初中阶段学生已经学习过三视图，对三视图已经有所了解，避免重复学习。

（二）新旧教材习题设置比较

在习题内容的设置上，旧教材是按照习题的难度进行归类，A 类是基础题，题型相对简单，多是对概念或定理的理解与简单应用，适合基础掌握不牢固的学生；B 类为拔高题，增设隐含条件，以考察学生的思维能力，培养学科素养为目的的题型，适合基础知识牢固，思维活跃的学生。新教材将习题拓展到了三类，划分的更加细致，第一类“复习巩固”主要是用来巩固所学的知识，加深对概念的理解；第二类“综合应用”主要是考察学生对概念和定理的掌握程度；第三类“拓广探索”这一类题多是探究类和开放类题型，主要是培养学生的创新意识和探究思维。

四、例习题类型比较

新旧教材中的例习题主要分为以下几种，见下图。

图1 新旧教材题型数量柱状图

从题型数量柱状图上我们可以看出，新旧教材在题型的种类上没有发生太多的改变，题型比较丰富多样，就各题型的数量而言，判断题和简答题的差距比较明显，新教材在判断题和简答题的题量上有所增加，相对应的填空题与作图题稍作删减，其主要原因有：一是判断题有助于培养学生的分析能力、判断能力以及理解能力，提高学生的逻辑推理和数据分析的核心素养；二是有目的增加简答题的数量可以使得学生能够更好地从生活中的立体几何中抽象出几何体的特征，培养学生的空间观念，为后面的点、线、面位置关系的知识学习做铺垫。

五、例习题难度比较

（一）例习题综合难度模型

根据立体几何部分例习题的特性，本文在鲍氏综合难度模型的基础上进行了改良。立体几何部分内容中属于符号运算的题型，未含有复杂类的符号运算，也未出现属于“科学情境”水平的例习题，故将各难度水平因素均划分为三个水平，将简单符号运算和复杂符号运算划分为符号运算，将背景类中“科学情境”难度水平删除，下面是改良后的例习题综合难度水平划分表：

例习题综合难度计算公式：

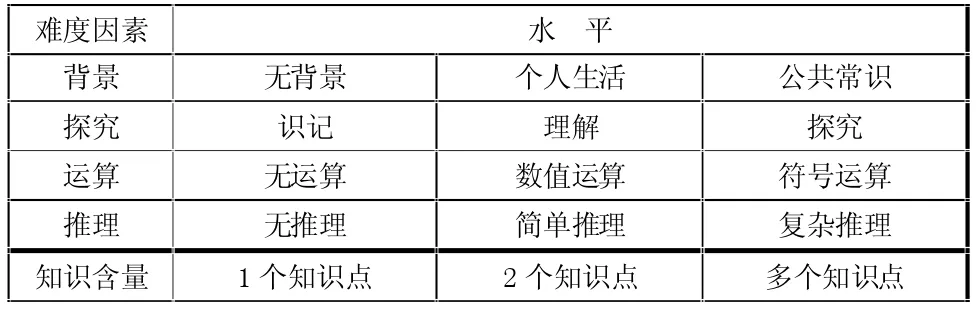
表1 数学例习题的改良后的综合难度因素与水平划分表

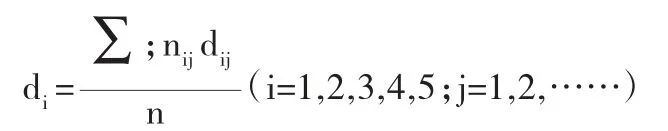
其中，di表示第i 个难度因素上的加权平均值；dij表示第i个难度因素的第j 个水平的权重。我们直接采用等级权重，即dij=j；nij则表示这套教材例习题中属于第i 个难度因素的第j个水平的题目个数，而n 是样本总数。显然，对任何i，都有∑=n。[1]

（二）各难度水平的分析

根据上面的综合难度分布框架和难度系数计算公式，分别从五个难度对数据进行比较分析，最后再利用所计算出各难度的加权平均进行整体分析。

1.在背景上的差异分析。经统计，属于“无背景”难度水平的例习题，旧教材占86.67%，新教材占90.27%；属于“个人生活”难度水平的例习题，旧教材占7.18%，新教材占5.75%；属于“公共常识”难度水平的例习题，旧教材占6.15%，新教材占3.98%。

由此可知，新教材在“无背景”方面的例习题要比旧教材多4 个百分点，属于无背景难度的例习题均是基础题，因此新教材中的例习题重在考察学生对于所学知识的掌握程度，加深学生对于概念的理解，相应的新教材在属于“个人生活”和“公共常识”两个难度水平的例习题降低了两个百分点，从整体来看属于背景难度的各个水平呈现逐渐下降的趋势，但高达80%的无背景水平的例习题，无疑使得学生产生厌倦感，因此在教学过程中，要紧密联系生活实际，把比较抽象的立体几何和生活中的实例相结合，便于教学。[2]

2.探究上的差异分析。经统计，新旧教材在立体几何部分，在探究难度上，属于“识记”水平的例习题新教材占18.58%，旧教材占17.95%；属于“理解”水平的例习题新教材占63.27%，旧教材占61.54%；属于“探究”水平的例习题新教材占18.15%，旧教材占20.51%。

因此，通过统计我们可以发现在立体几何部分，新旧教材在“理解”水平的例习题占比较高，达到了60%左右，属于“识记”和“探究”水平的例习题占比相对平衡，只达到了20%，新旧教材在探究层次整体呈现出类似“山峰”的变化趋势，说明新旧教材在考查学生对数学概念、定理的理解方面比较重视。

3.运算上的差异分析。经统计，新旧教材在立体几何部分，属于“无运算”水平的例习题分别占82.74%和78.97%；属于“数值计算”水平的例习题分别占10.62%和12.31%；属于“符号计算”水平的例习题分别占6.64%和8.72%。我们可以清晰地看到新旧教材在运算层次的各个难度水平的分布类似，属于“无运算”水平的例习题占了绝大部分，尤其是在直线与平面的位置关系章节。

4.推理上的差异分析。经统计，新旧教材在立体几何部分，属于“无推理”水平分别占19.03%和27.2%；属于“简单推理”水平分别占63.27 和58.97%；属于“复杂推理”水平分别占17.70%和13.85%；可以看出，在“简单推理”和“复杂推理”两个水平上新教材的例习题数量都要高于旧教材，说明新教材例习题的“推理”水平整体上要高于旧教材。

5.知识点上的差异分析。经统计，新旧教材在立体几何部分，属于“一个知识点”水平的例习题中新教材占59.73%，旧教材占61.03%；属于“两个知识点”水平的例习题中新教材占24.78%，旧教材占27.69%；可以看出，新旧教材在“1～2 个知识点”水平的例习题数量差别不大，都比较重视考察学生对基础知识理解，属于“多个知识点”水平的例习题中新教材占15.49%，旧教材占11.28%，在多个知识点层次的例习题中，新教材要高于旧教材4 个百分点，也就是说新教材在例习题的知识含量上略有增加。这也使得新教材例习题的难度增大，因此，教师在例习题的教学过程中也要加强对各知识点的渗透。

6.综合难度分析。我们运用鲍建生综合难度计算公式计算出新旧教材例习题在各个难度的加权平均，在背景难度上，新教材为1.14，旧教材为1.19；在探究难度上，新教材为2.00，旧教材为2.03；在运算难度上，新教材为1.24，旧教材为1.30；在推理难度上，新教材为1.99，旧教材为1.89；在知识点难度上，新教材为1.56，旧教材为1.50。下图是根据计算结果得出的例习题综合难度雷达图。

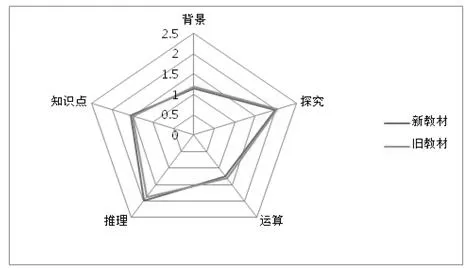
图2 例习题综合难度雷达图

根据所得的计算结果和雷达图，可以发现新教材在“推理”和“知识点”两个因素上占优，在“运算”和“背景”方面稍显劣势，这说明新教材重视例习题的知识点含量和逻辑推理，体现了新课标提高课程综合性的指导思想。此外，图中的两个雷达图，均有下降的趋势，这说明新旧教材在“背景”水平的都偏低，这也是高中教材例习题在立体几何部分相比于其他部分的显著差异，也体现了立体几何部分的例习题更加注重数学题本身的理论深度，降低与生活实际的联系的趋势。[3]

六、立体几何部分例习题的教学建议

（一）以学生为主，发展学生的数学核心素养

《普通高中数学课程标准（2017 版）》中强调“以学生发展为本，立德树人，提升素养”，教师在例习题的教学过程中，可以通过模型或实物，创设适当的问题情景，引导学生发现例习题中的隐含条件，采用哪些知识点可以进行解题，以助于提升学生的直观想象、逻辑推理、数学运算和数学抽象素养。

（二）重视信息技术的运用，提高学生的学习兴趣

例习题中属于“无背景”水平难度的大约占90%，这样使得学生在做例习题时比较抽象，不易理解，无形中增加了解题的难度，大部分学生都是首次接触空间几何体的概念，一时间难以从“二维图形”转换到“三维图形”，这也使得教学的难度大增。因此在教学过程中教师可以运用计算机软件将学生难以理解的空间几何体呈现出来，帮助学生清晰地认识空间几何体的结构特征，逐渐掌握如何在平面上表示空间图形的方法和技能，为学生理解和掌握图形几何性质提供直观，提升学生的学习兴趣。的教学原则

（三）遵循从整体到局部，从具体到抽象

立体几何部分的例习题也是遵循从整体到局部，从具体到抽象的教学原则，例如在证明面面垂直时，很多学生不知从何处着手，此时可以引导学生从证明面面垂直这个整体上转换到证明线面垂直上来，同时教师在例习题的教学过程中，可以利用生活中的实例或模型，抽象出空间立体图形，进而利用空间立体图形研究点、线、面的位置关系，促进学生空间观念的形成。[4]

（四）锻炼学生逻辑思维，加快空间观念的形成

立体几何部分的教学目的是培养学生形成空间观念和锻炼学生的逻辑推理能力，立体几何部分的例习题，一题多解的题型也是屡见不鲜，因此教师在一道例题的讲解过程中，可以多角度的提出不同的问题，加快学生对概念的理解，以便抓住解题的要点，理解例习题的考点是什么，锻炼学生的逻辑思维能力，加快空间观念的形成。但是问题的难易程度会影响学生的心态，因此在提出多角度的问题时，要根据不同层次的学生选择性地提问。

（五）避免过量的理论推理

在例习题的教学过程中存在多种定理的同时运用，这也使得证明过程中出现大量的理论推理的现象，面临这种情况时，如果学生对于概念的理解不够，就会出现多种定理和概念的混乱，这时教师就需要采用具体的实物配合理论证明的过程，使得证明过程变得清晰明确，但也要避免采用过量的实物，即避免从一个极端走向另一个极端的现象发生。