基于时频分析和SVM的发动机齿轮箱故障诊断

高坤明，张衡，张振京，宋业栋，严孝强

（潍柴动力股份有限公司，山东潍坊 261061）

0 引言

齿轮箱是柴油机重要的部件之一，通过齿轮的啮合和传动能够实现力从曲轴定时齿轮到凸轮轴齿轮、喷油泵齿轮以及机油泵齿轮的传递，齿轮箱的工作状态对发动机的性能影响较大[1-3]。通常对柴油机齿轮箱的故障处理方式大多采用定期检查保养，这种方式效率低、成本高，且缺乏预见性，因此研究智能的故障诊断方法显得尤为重要。卢锦玲等[4]结合相关向量机和遗传算法，提出了一种风机齿轮箱的故障诊断方法，实现了齿轮箱的多故障分类。王二化等[5]取故障诊断的特征值为小波包的各个频段的能量比，利用神经网络方法对特征值进行分类，从而实现了齿轮的故障诊断。

时频分析方法通过将一维的振动信号映射到二维时频面，能够提供更多的时域信号无法提供的特征信息[6-7]。李飞行等[8]针对航空发动机的振动监测和故障诊断，提出了一种基于时域滑窗的短时傅里叶变换的时频分析方法，实现了对发动机的特征信息的提取和故障诊断。蔡艳平等[9]基于阈值筛选的变分模态分解的方式提出了一种时频分析方法，实现了发动机故障的识别诊断。

在故障识别和分类中，主要方法有深度学习[10]、BP神经网络[11]和支持向量机[12-13]等。张俊红等[14]针对柴油机气门故障诊断问题，提出了一种基于支持向量机和局部均值分解相结合的诊断方法，并且验证了该方法的准确性。

为了进一步提高发动机故障诊断的精度，本文在相关研究的基础上，基于发动机齿轮箱振动数据，结合时频分析方法，提取时域分析和频域分析特征值，并构建特征矩阵，最后通过支持向量机进行故障诊断。

1 信号时频分析与特征提取

从复杂的振动信号中提取能够反映故障原因的特征参数是故障诊断的关键，本文将利用时域和频域分析方法分析信号，并从中提取故障特征。

时域分析是最基础的信号分析方法，由于其曲线特征简单直观，常用于初期故障诊断，能够快速分析出系统振动情况。时域分析特征参数主要有峰值、均方根值、方根幅值、绝对均值、斜度和峭度等，通过求取部分实验数据的各时域特征值后，本文采用峭度作为时域分析的特征值，峭度公式如下所示：

式中：x为信号；N为数据点的个数。

频域分析主要是将信号分解为周期子信号进行识别，短时傅里叶变换（STFT）是最常用的一种线性频域分析方法之一，可以通过时间窗口内的一段信号来表示某一时刻的信号特征，在STFT变换过程中，频谱的时间与频率分辨率由所选取的窗的长度决定，公式如下所示，

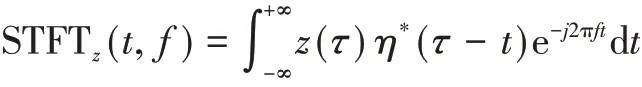
式中：z(t)为信号；η(t)为给定的窗函数；t和f分别为时间和频率；STFTz(t,f)为信号z(t)在t时刻、频率为f的能量分布。

时域信号进行傅里叶变换后将信号在时间序列上的振动情况转换到在频率序列上的振动情况，频域分析能够得到诸多在时域分析中难以获得的信息，其中本文采用能量作为频域分析的特征值，能量的计算公式如下：

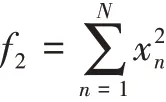
小波变换是20世纪80年代后期发展起来的一个新的数学分支，小波是指Ψ(t)经过伸缩和平移后形成的一簇函数，公式如下所示：

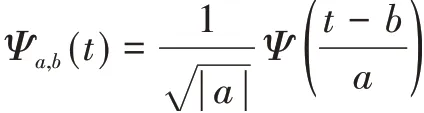
式中：Ψ(t)为振荡衰减且具有紧支集的函数；参数a为尺度因子；参数b为平移因子。

对任意信号x(t)，其小波变换的定义如下：

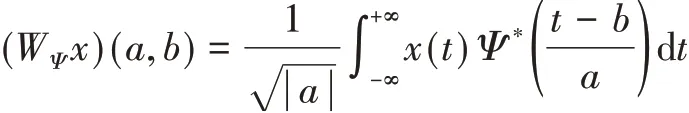
式中：Ψ*(t)为Ψ(t)的共轭。

可以证明，只有当小波函数满足容许条件时，即：

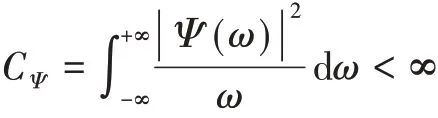
式中：Ψ(ω)为Ψ(t)的Fourier变换。

当上式成立时，才能用小波变换(WΨx)(a,b)重构原信号x(t)，此时：

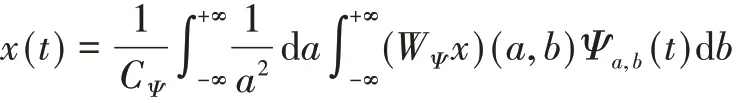
本文通过DB10小波基对振动数据进行3层小波包分解，分别提取8个频段的小波包系数矩阵奇异值和各频段能量百分比，作为时频分析中的特征值。

2 故障识别

2.1 故障识别方法

SVM是建立在统计学习理论基础上的一种通用机器学习方法，在解决小样本、非线性、高维问题中有诸多优势，具有良好的泛化能力，SVM的主要思想是在输入空间建立一个分类超平面，以使两个样本集到达分类超平面的距离最大。图1所示为SVM分类示意图，原形和方形分别代表两种类型，H1、H2上的样本为支持向量。

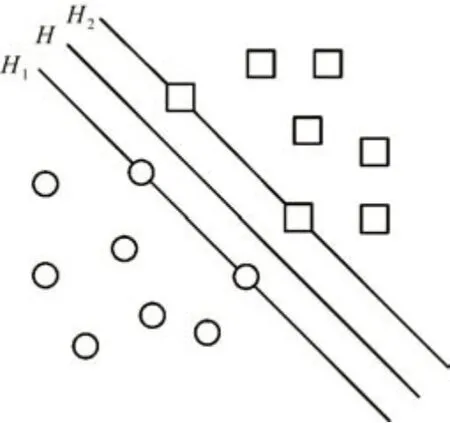
图1 SVM分类示意

最终可以转化为求解式所示二次规划问题，即：

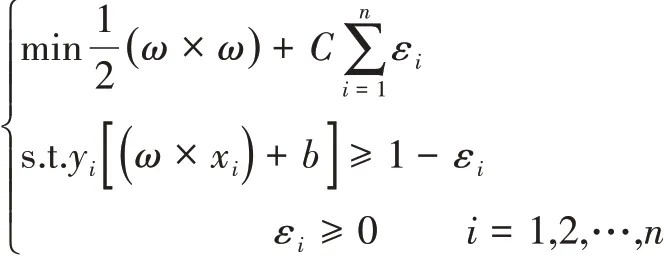
式中：C和εi分别为惩罚参数和松弛变量。

通过引入Lagrange乘子αi(i=1,2,…,n),可以得到：

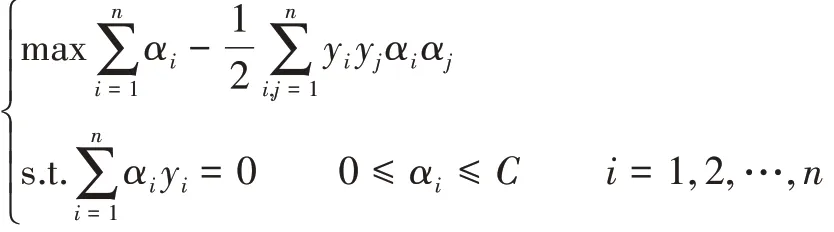
求解式可得式所示的决策函数，即：

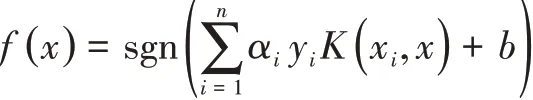
式中：K(xi,x)表示核函数。

一般采用如下式所示形式，

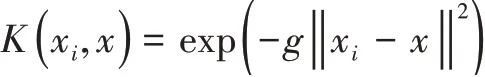
2.2 故障识别流程

图2所示为具体的诊断流程，主要包括如下几个步骤：

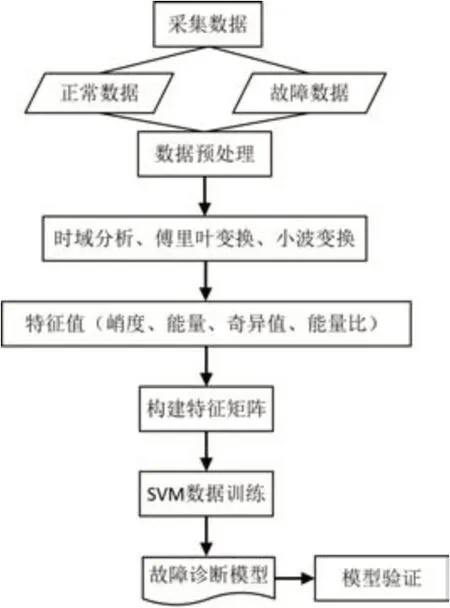
图2 故障识别流程

（1）将实验台架采集的正常数据和故障数据进行初步处理，要求每组数据的采集时间和数据长度一致；

（2）对数据进行预处理，并实现信号的时域读取，傅里叶变换和小波分析；

（3）提取特征值，包括时域信号的峭度值、频域信号的能量值以及小波包系数矩阵奇异值和各频段能量百分比；

（4）构建以特征值为元素的特征矩阵；

（5）利用支持向量机对信号进行训练，并得到故障诊断模型，并将为参加训练的数据导入验证训练模型的准确性。

3 实验验证

3.1 数据采集

为了验证该方法的有效性，本文从数据采集着手，借助实验室台架资源，利用自主开发的发动机振动信号采集装置对发动机齿轮箱进行振动信号的采集。其中对于齿轮箱的处理依据实验和方法验证的需求，首先采集齿轮箱处于正常状态下的数据，然后将发动机齿轮箱衬套磨损后在相同工况下采集齿轮箱处于故障状态时的数据，发动机运行工况为750 r∕min，0扭矩，采样频率为102 400 Hz，数据采集使用一个三轴传感器，传感器的安装位置为齿轮室的平面部，进过数据分析得知，三轴传感器的Y轴方向为振动的主方向。从实验数据中选取40组数据备用，包括20组训练数据和20组测试数据，其中20组训练数据由10组正常数据和10组故障数据组成，20组测试数据同样由15组正常数据和5组故障数据组成。

3.2 时域分析

将训练数据进行时域分析，图3和图4为训练数据中正常数据一和故障数据一的时域波形图，从时域图中可以看出，齿轮箱故障的振动加速度幅值超过10g的部分明显多于正常时的振动加速度。为了更好地从时域图中获得更加直观的的信息，进行时域特征分析，时域分析特征值为峭度值，峭度值是表征振动幅值概率密度的陡峭程度，故障越明显，峭度值越大。

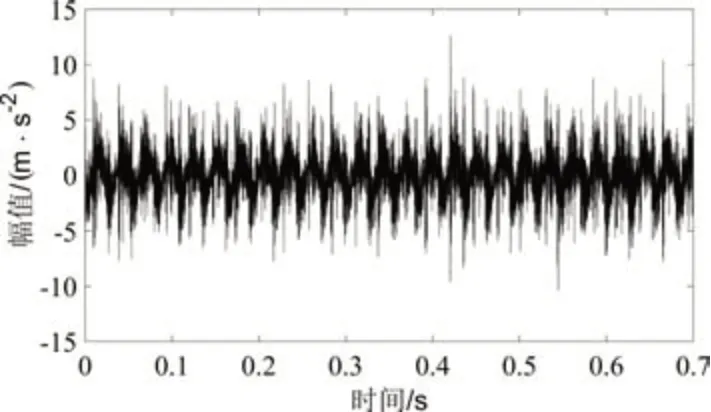
图3 正常工况时域图

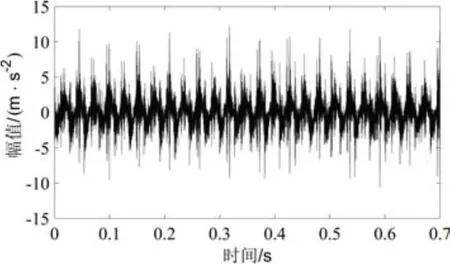
图4 故障工况时域图

将20组训练数据进行时域信号的峭度值的求解，求解结果如图5所示，由图可知，正常数据的峭度值大都小于故障数据的峭度值，可以将峭度值作为区分正常数据和故障数据的特征值。

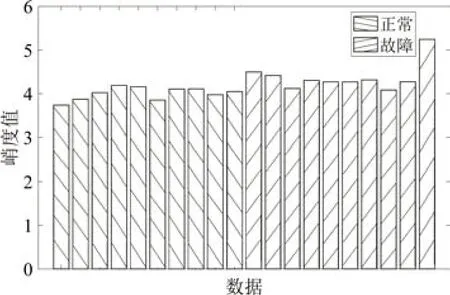
图5 峭度值柱状图

3.3 频域分析

频域分析是将时间与振幅的对应关系分解到频率与振幅的对应关系上，实现原信号从时域到频域的变换，从频域曲线中可以挖掘时域信号无法获得的信息，正常数据一和故障数据一的频域曲线如图6和图7所示。

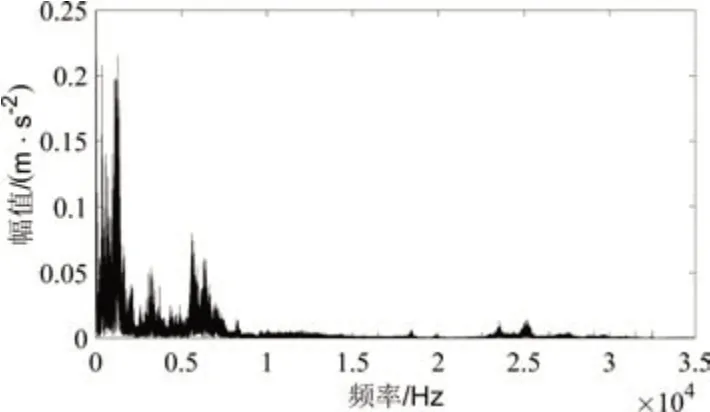
图6 正常工况频域图

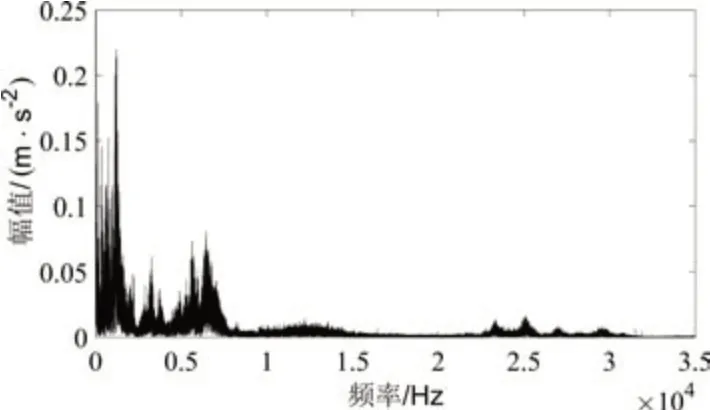
图7 故障工况频域图

从正常数据和故障数据的频域图中可以看出，在频率值为8000~35000Hz，故障数据的振动幅值明显大于正常数据的振动幅值。频域分析特征值为能量值，能量值是表征整体振动幅值大小，通常故障越明显，能量值越大。

将20组训练数据进行频域信号在8000~35000Hz频段之间的能量值的求解，求解结果如图8所示，由图可知，正常数据的均方根值明显小于故障数据的均方根值，可以将均方根值作为区分正常数据和故障数据的特征值。

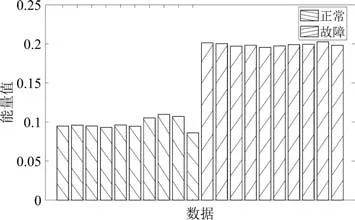
图8 能量值柱状图

3.4 时频分析

时频分析能够分析时域和频域难以分析的非平稳信号，采用DB10小波基对振动数据进行3层小波包分解，分别提取8个频段的小波包系数矩阵奇异值和各频段能量百分比，小波包系数矩阵奇异值和能量百分比计算结果如图9~10所示。

从图9可以看出，正常数据和故障数据8个频段小波包系数奇异值在第1个频段正常数据的小波包系数奇异值大于故障数据，从第2到第8个频段正常数据的小波包奇异值小于故障数据，呈现了一定的规律性，因此可以将小波包系数矩阵奇异值作为区分正常数据和故障数据的特征值。

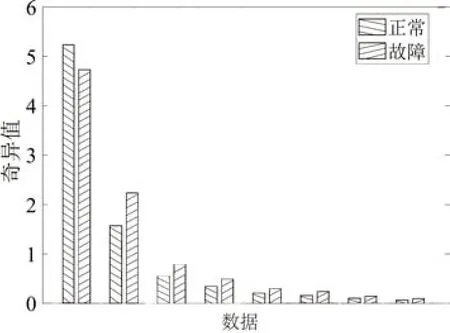
图9 小波包系数矩阵奇异值

从图10中可以看出的规律性和小波包系数矩阵奇异值柱状图相同，因此可以将小波包各频段的能量比值作为区分正常数据和故障数据的特征值。

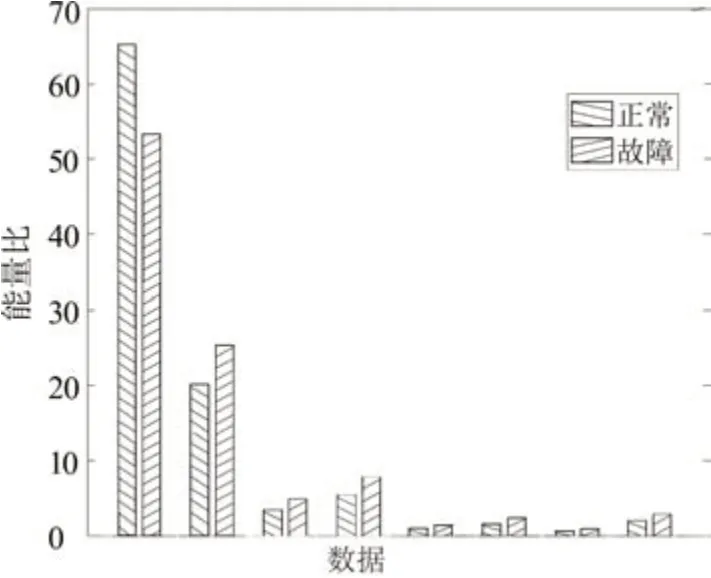
图10 小波包各频段能量比

3.5 诊断模型及验证

以稳态工况下柴油机齿轮箱振动实验选取的20组训练数据为训练样本，其中正常数据一的特征值如表1所示，故障数据一的特征值如表2所示，建立齿轮箱振动数据的SVM故障诊断模型，利用训练好的齿轮箱振动数据SVM故障诊断模型对测试数据进行故障诊断，故障诊断模型验证结果如图11所示，图中渐变颜色坐标值代表测试数据量的大小，坐标0表示正常状态，坐标1表示故障状态。（0，0）坐标值代表状态真实值为正常，状态预测值也为正常；（1，1）坐标值代表状态真实值为故障，状态预测值也为故障，所以坐标（0，0）和坐标（1，1）代表故障诊断准确。（0，1）坐标值代表状态真实值为故障，但是状态预测值为正常，这样的情况为漏警；（1，0）坐标值代表状态真实值为正常，状态预测值为故障，这样的情况为虚警。从故障诊断模型验证结果图中可以看出，本文通过训练数据得到的SVM故障诊断模型的诊断正确率为100%。

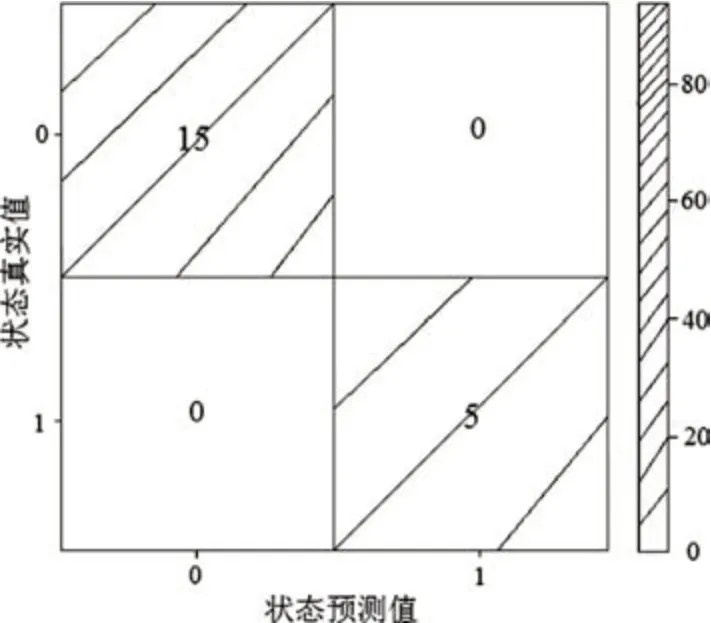
图11 故障诊断模型验证结果

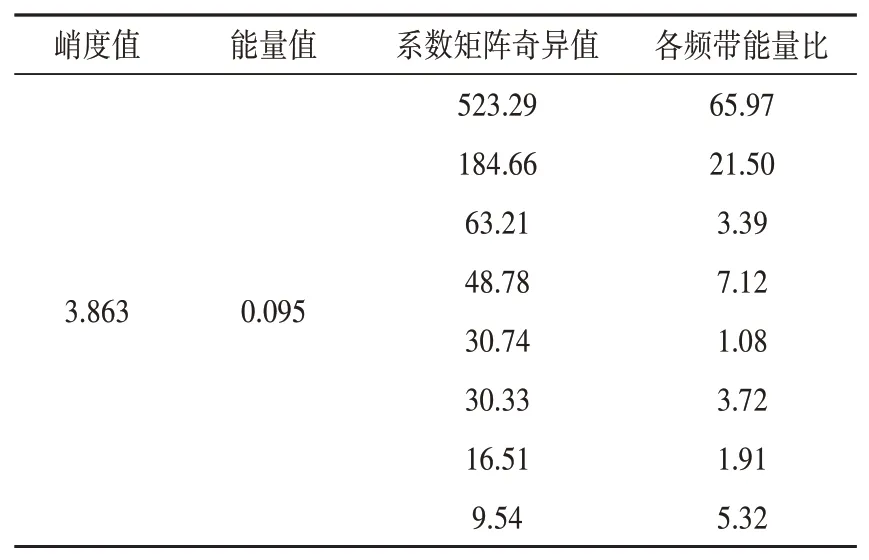
表1 正常数据一特征值

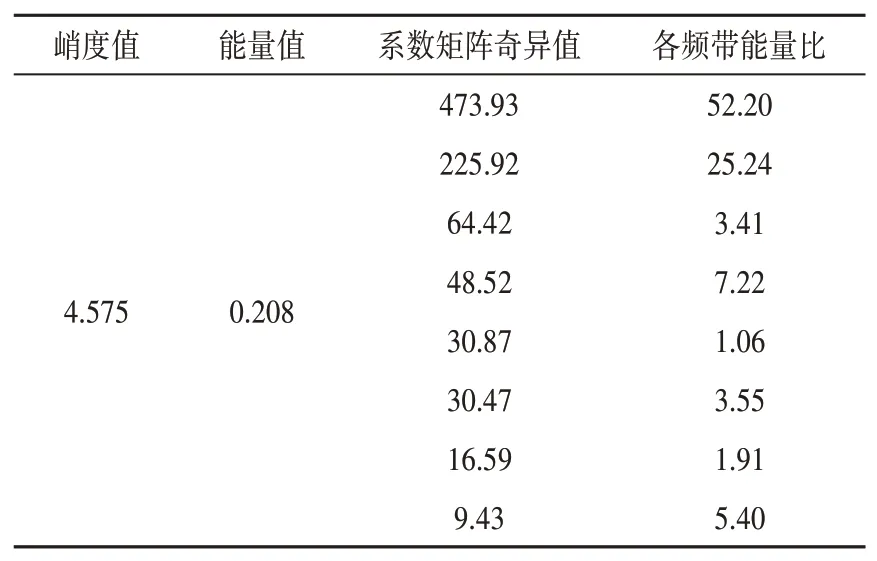
表2 故障数据一特征值

4 结束语

本文基于发动机怠速工况下的齿轮箱振动数据，结合时域分析方法、傅里叶频域分析方法和小波变换时频分析方法对实验数据进行预处理，提取时域峭度值、频域能量值、小波包系数矩阵奇异值和小波包各频带能量比10个特征值，并构建特征矩阵，导入线性支持向量机进行训练，得到故障诊断模型。通过测试数据的验证结果表明，故障诊断模型能够完全实现故障数据的识别，本文的工作可以为故障诊断方法设计提供一定的参考。