基于非等温三相流模型的欠平衡钻井井底压力预测

FALAVAND-JOZAEI A，HAJIDAVALLOO E，SHEKARI Y，GHOBADPOURI S

（1. 伊斯兰阿萨德大学阿瓦士分校机械工程系，阿瓦士 6134937333，伊朗；2. 阿瓦士沙希德查姆兰大学机械工程系，阿瓦士 6135783151，伊朗；3. 阿瓦士沙希德查姆兰大学钻井研究中心，阿瓦士 6135783151，伊朗；4. 亚苏季大学机械工程系，亚苏季 7591874934，伊朗）

0 引言

欠平衡钻井（UBD）是一种重要的高效钻井方法。在欠平衡钻井中，通过将气体注入到钻井液中来控制井底压力，而当固体颗粒（钻屑）进入到该气-液两相流中时，井筒环空内形成气-液-固三相流。在钻井作业中，井筒内的钻井液温度会发生变化，这是钻井液和周围地层间热量传递导致的。而钻井液的性能与温度紧密相关，对钻井液温度的计算是否准确直接关系到是否能对压力分布和井底压力（BHP）做出准确的预测。

许多研究者已经对井筒内热量传递现象进行了研究，应用解析和数值方法来计算钻井液的温度。Ramey[1]、Holmes和 Swift[2]、Arnold[3]、Kabir等[4]采用半瞬态法求解，即认为地层内部的热量传递是瞬态的，而井筒内的热量传递是稳态的。Raymond[5]首次建立了数值模型来对瞬态和拟稳态两种情况下钻井液温度分布进行预测。Marshall和Lie[6]建立了数值模型来计算稳态和瞬态两种情况下井筒内温度分布，该模型使用有限差分法，考虑了单向流。Song等[7]使用均相模型得出了井内循环气液两相流体时的压力和温度分布，模型考虑了黏性耗散、钻柱旋转以及钻头能量的影响。Perez-Tellez等[8-9]提出一种机械性模型对钻井作业中井筒内的井底压力和压力分布进行评估。Khezrian等[10]考虑地温梯度的影响，使用稳态两相流模型对欠平衡钻井中井筒环空内气-液两相流进行模拟。Shekari等[11]使用瞬态两相流模型对欠平衡钻井作业中井筒环空内气-液两相流进行模拟。Ghobadpouri等[12]求解了钻井过程中井筒环空内两相流体（气体和液体）控制方程，考虑了地温梯度以及储集层排液的影响，但是没有讨论钻屑、钻井液与周围地层间的热量传递对压力分布和井底压力的影响。Ghobadpouri等[13]使用一维稳态三相流模型对环空中气-液-固三相流进行模拟，证明与使用两相流模型相比，使用三相流模型能更准确地预测井底压力。该研究也没有讨论钻井液与周围地层间热量传递对压力分布和井底压力的影响。Hajidavalloo等[14]发现与设定地温梯度的两相流模型相比，考虑能量方程的两相流模型能更准确预测欠平衡钻井井底压力。Falavand-Jozaei等[15]研究了影响欠平衡钻井作业中气-液两相流温度和压力分布的重要因素。Hajidavalloo等[16]研究了单相流条件下钻井作业中温度变化对井底压力预测结果的影响。

上述研究中，考虑温度影响的数值模型较少，模型也较简单。大多数数值模型没有考虑环空中固相的存在以及固相对流体与地层间热量传递的影响，与实际不符。钻屑的存在及其在井筒内的热量传递可能会影响井底压力，并对控制井眼清洗的参数施加限制。因此，本文在建立欠平衡钻井三相流模型时，考虑含钻屑钻井液与地层瞬态热反应的影响，从而获得更加准确的井底压力预测结果。

1 模型建立

如图1所示，在欠平衡钻井作业中，气-液两相流体通过钻柱泵入井筒内，该流体穿过钻头，并携带钻屑。气-液两相流体、地层流体与钻屑在环空内混合形成气-液-固三相流体沿着环空上返。鉴于产出气体与注入气体的热物理性质非常接近，可以认为地层中气体和注入到井筒内的气体组成一种以相同速度流动的混合物。同理，也可以认为注入的液体和地层流体组成一种在环空中以相同速度流动的混合物。

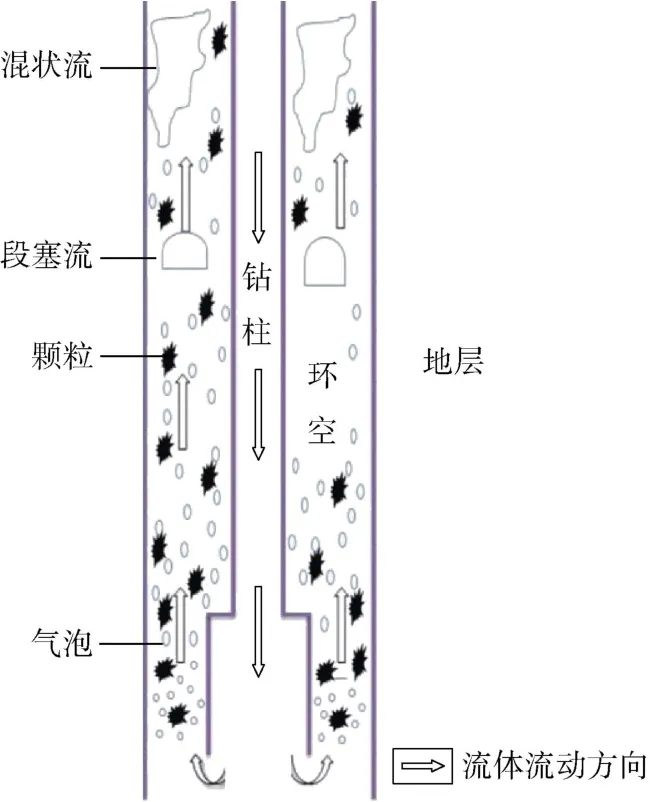
图1 欠平衡作业中流体循环示意图

三相流模型考虑到每一相单独的流速，应用该模型对环空中气-液-固三相流体进行模拟。在该模型中，假设井筒内流体是一维的，液相不可压缩，气相可压缩。相间以及相与井壁间的摩擦系数考虑了紊流剪应力和黏滞效应的影响。每个时步都考虑了钻柱和环空内的稳态一维气-液-固三相流，流体性质可变。在流体循环期间任意点处温度会随着时间而变化，因而井筒与周围地层之间的热量传递是瞬态的。

1.1 井筒内热量传递

1.2 地层中热量传递

1.3 求解方法

首先在稳态条件下依据地温梯度对沿井筒温度分布进行预测，然后可将连续性方程和动量方程简化为6个微分方程。这6个方程与（5）式、（6）式组成了含8个方程的方程组，其中有8个未知数（3个速度未知数、3个体积分数未知数、1个压力未知数和1个气体密度未知数）。将这些方程离散化得到1组耦合的非线性代数方程式，可由牛顿法求解。方程的离散形式详见文献[22]。

边界条件为：井口压力等于节流压力；井口处气体密度可以由气体状态方程求得。

采用 Bratland[22]提出的算法，使用牛顿方法，就能计算出速度、压力和体积分数。以下是具体步骤。

①确定初始条件。初始时刻（t=0）井筒内和地层的温度条件按照地温梯度设定。依据初始时刻钻柱和环空内流体温度分布，使用上述方程组计算初始时刻体积分数、速度和压力。

②使用（7）式和井底边界条件估算钻柱内流体温度分布。为了估算钻柱内流体温度分布，需要对当前时步环空内流体温度分布进行假设。将上一时步的环空内流体温度分布作为初始假设。

③基于新估算的钻柱内流体温度分布，使用（8）式和井底边界条件估算环空内流体温度分布。同样，需要对当前时步相邻地层内的温度分布进行假设。将上一时步的相邻地层内温度分布作为假设。

④基于新估算的环空内流体温度分布，使用（11）式对地层温度进行估算。将估算结果与初始假设进行对比，如果误差可接受，则进入下一时步；否则，基于步骤②、③中新估算的钻柱和环空内流体温度分布，再次计算体积分数、速度和压力。然后，使用当前时步的环空和地层内温度分布作为新的假设进行下一时步的计算。重复上述过程，直到完成总循环时间的计算。

2 模型验证

通过与Kabir等模型[4]进行对比，对本文模型进行验证。图2为流体循环44 h后钻柱和环空内流体温度与井深关系曲线，本文模型与Kabir等模型的计算结果吻合非常好，最大偏差约为0.3%。

图2 本文模型与Kabir等模型流体温度分布计算结果对比

3 模型应用

使用文献[8]中的Muspac 53井现场数据，应用本文建立的三相流模型（考虑传热的三相流模型）进行计算和分析。

图3为使用不同模型预测的压力分布曲线。计算基本条件为：地温梯度0.028 3 K/m，钻速6 m/h，流体循环时间16 h。与Ghobadpouri等[13]提出的三相流模型、Hajidavalloo等[14]提出的考虑传热的两相流模型和其他两相流模型（包括WELLFLO软件）[29]相比，本文建立的考虑传热的三相流模型能够给出更加准确的预测结果。将使用考虑传热的三相流模型和三相流模型预测的井底压力与现场数据进行对比，考虑传热的三相流模型预测误差为5.7%，而三相流模型预测误差为11.3%，进一步验证了本文模型的准确性。

图3 不同模型压力分布计算结果对比

图4显示了源项对温度分布曲线的影响，包括井筒内黏性耗散、旋转钻柱与井壁间摩擦以及钻头钻进产生的热量。该图证实了将源项加入能量守恒方程中的必要性，忽略源项的影响导致井底温度预测结果减小6.1 K。

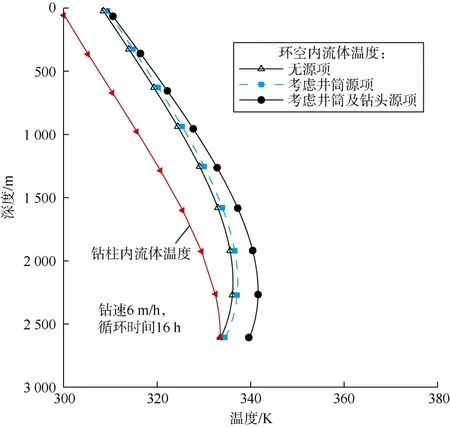
图4 源项对温度分布的影响

图5显示了钻速恒定条件下环空内流体温度分布与循环时间的关系。随着循环时间的增加，井筒下部环空内流体温度变化非常明显，初期变化非常迅速，之后逐渐放缓。如图5所示，井底处地层温度比环空内流体温度要高得多，但在井口处差异很小。此外，环空内流体温度没有在井筒内最低点达到其最高值。这是因为，既然环空内流体温度低于周边地层温度，那么环空内流体从周围地层吸收热量。只要环空内流体从周围地层获得的热量大于向钻柱内流体传递的热量，环空内流体温度将随着向上流动而增加。随着环空内流体向上流动，环空周围地层温度降低，环空流体获得的热量减小，同时环空内热量向钻柱内温度更低的流体传递。当获得热量等于损失热量时，环空内流体温度达到其最高值。在本文算例中，流体循环16 h后，环空流体最大温度出现在2 251 m处。

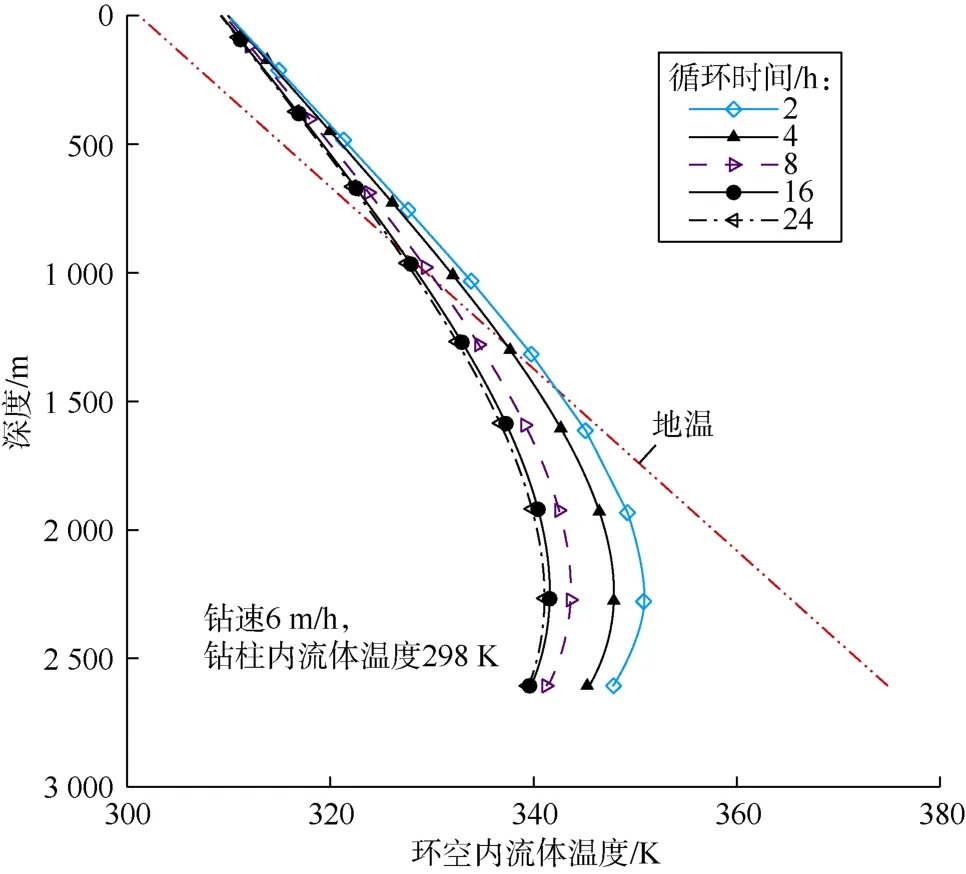
图5 环空内流体温度分布与循环时间的关系

图6显示了井口、井底环空内流体温度和井底地层/环空界面温度随循环时间的变化。初始阶段，井底地层/环空界面和井底处环空内流体温度随着时间增加急剧下降；在稍后两者相差约4 K时开始缓慢下降；大约16 h之后，两个温度不再随循环时间变化而变化。初始阶段，井口处环空流体温度随着时间增加而升高，近4 h后温度达到恒定值。

图6 井口、井底环空内流体和井底地层/环空界面温度与循环时间关系

图7和图8显示了液相和气相流量对环空内流体温度和压力分布的影响。图7a显示，随着液相流量增大，井口附近环空内流体温度升高，而井底附近环空内流体温度降低。通过提高液相流量可以增加混合物比热容，因此井底与井口环空内流体温度差异减小。图7b显示，当液相流量从0.503 m3/min增加到0.603 m3/min时，井底压力增加了大约1.76 MPa，这主要是环空内混合物密度增加所导致的。图8a显示，随着气相流量增大，井底附近环空内流体温度升高，而井口附近环空内流体温度降低。因为气相比热容小于液相比热容，环空内混合物比热容随着气相流量增大而减小，所以井底与井口环空内流体温度差异随着气相流量增大而增加。图8b显示，当气相流量从15 m3/min增加到20 m3/min时，井底压力减小了大约0.76 MPa，这主要是因为环空内混合物密度随着气相流量增加而减小。

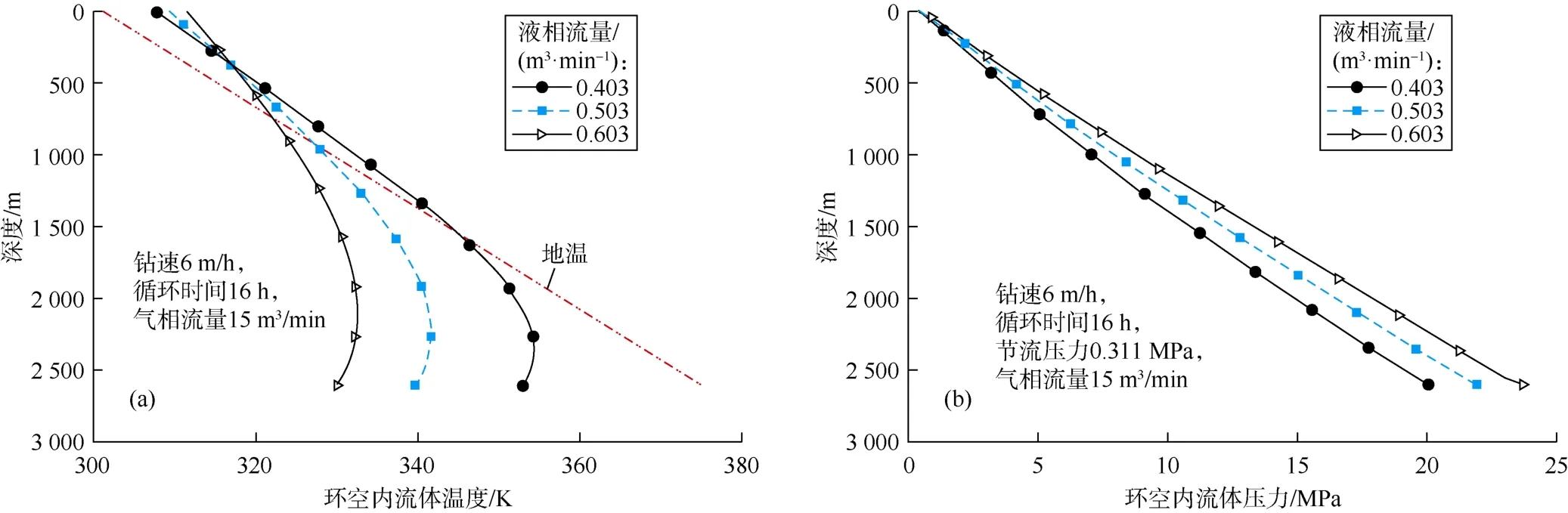
图7 液相流量对环空内流体温度（a）和压力（b）分布的影响

图8 气体流量对环空内流体温度（a）和压力（b）分布的影响

图9显示了气相流量对气相和固相体积分数随井深分布的影响。随着井深减小，气相体积分数增加，固相体积分数减少；同样，随着气相流量增加，气相体积分数增加，固相体积分数减少。井底处固相体积分数的突然变化归因于井筒直径的变化，因此清洗井眼最重要的位置为井筒底部。如图9a所示，通过增加气相体积流量，井筒上部发生流型转变。

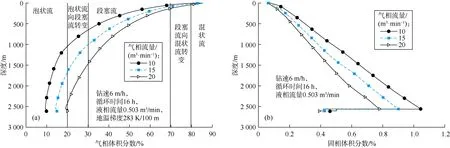
图9 气相流量对气相（a）和固相（b）体积分数随井深分布的影响

图10显示了地层导热系数对井底环空内流体温度随时间变化的影响。图10a显示，井底环空内流体温度随地层导热系数增加而大幅升高。图10b显示，与井筒上部相比，地层导热系数对井筒底部环空内流体温度影响较大。图11显示了文献[8]中Iride 1166 井储集层流体流入对环空内流体温度分布的影响，可以看出，当有储集层流体流入时井底处环空内流体温度提高了大约10 ℃。需要说明的是，本文除图11使用文献[8]中Iride 1166 井数据外，其他图均使用文献[8]中的Muspac 53井数据。

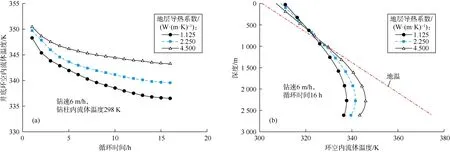
图10 地层导热系数对井底流体温度随时间变化（a）以及环空流体温度分布（b）的影响

图11 储集层流体流入对环空内流体温度分布的影响

图12显示了液相和气相比热容对环空内流体温度分布的影响。混合物比热容随着液相和气相比热容增加而增加。图中显示，井底处环空内流体温度随着混合物比热容增加而降低，而井口处环空内流体温度随着混合物比热容增加而升高。需要注意的是，气相比热容增加对混合物比热容的影响大于液相比热容增加对混合物比热容的影响，这是因为气相比热容小于液相比热容。因此，气相比热容越大井底温度越低，井下工具破裂风险越低。液相和气相的比热容增加1倍，井底压力分别增大了大约0.12，0.17 MPa。

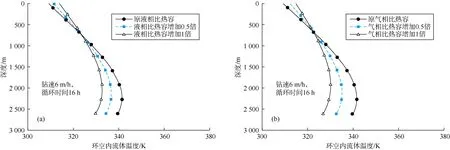
图12 液相（a）和气相（b）比热容对环空内流体温度分布的影响

4 结论

与两相流模型及其他仅考虑地温梯度的三相流模型相比，本文建立的考虑传热的非等温三相流模型预测欠平衡钻井井底压力的准确性更高。

井筒内黏性耗散、旋转钻柱与井壁间摩擦及钻头钻进产生的热源以及储集层油气流入对环空内流体温度分布有重要影响，进而对井底压力产生重要影响。

井底流体温度随着液相流量、循环时间、液相和气相比热容的增加而降低，随着气相流量的增加而升高。井底压力与气相和液相流量的相关性较强，液相流量增加则井底压力增大，气相流量增加则井底压力减小；井底压力与循环时间、液相和气相比热容的相关性较弱。

符号注释：

A——面积，m2；C——比热容，J/（kg·K）；d——直径，m；Fg——单位体积的重力，N/m3；Fij——单位体积的相间相互作用力，N/m3；Fv——单位体积的虚拟质量力，N/m3；Fw——单位体积的井壁摩擦力，N/m3；G——地温梯度，K/m；h——对流传热系数，W/（m2·K）；hlsp——液相的单相传热相关系数，W/（m2·K）；htp——两相流体间对流传热系数，W/（m2·K）；k——导热系数，W/（m·K）；Mg——气体摩尔质量，kg/mol；n——流型指数；p——压力，Pa；Δpij——压力修正项，即相界面压力与相内压力之间的压差，Δpis=0，Pa；q——质量流量，kg/s；r——半径，m；rpi，rpo——钻柱内半径和外半径，m；R——理想气体常数，8.314 J/（mol·K）；S——源项，W/m；t——时间，s；T——温度，K；Tf——地层和环空交界处的温度，K；Ua——环空内流体与周围地层间总传热系数，W/（m2·K）；Up——钻柱内流体与环空内流体间总传热系数，W/（m2·K）；v——速度，m/s；vd——钻速，m/s；x——深度，m；Z——气体压缩因子；α——体积分数，%；μ——黏度，Pa·s；ρ——密度，kg/m3。下标：a——环空内流体；f——地层；g——气体；l——液体；p——钻柱内流体；s——固体。