基于SWMM模型的排水分区参数率定
——以迁安市为例
2022-05-12王建富
王建富,郭 豪,秦 祎,张 超
(1.北京清华同衡规划设计研究院有限公司,北京 100083;2.清华大学环境学院,北京 100084;3.北京城建设计发展集团股份有限公司,北京 100037)
随着城市化建设的推进,硬化下垫面不断增加,导致降雨径流量增大,加剧污染负荷的产生和转移,从而产生因城市面源污染负荷增加引起的城市水体污染[1-2]。近几年,在海绵城市建设过程中,对城市面源污染的重视程度逐渐上升,采用以“绿色与灰色”“地上与地下”相结合的方式分区治理面源污染,形成“源头减排-过程控制-系统治理”的全过程治理体系,提高面源污染治理效果[1-3]。区域现状复杂且面积较大,须借助数学模型不断评估现状和方案效果,这增加了整体的工作难度和时间,因此,需要进一步提高数学模型的应用效率[3-5]。
目前,通过模型模拟产汇流是研究城市暴雨径流污染管理和控制的重要手段[6-7],其对研究城市面源污染的多边性和复杂性具有一定优势[6]。国内外应用的管网模型有SWAT模型、SWMM模型、InfoWorks ICM模型等[7-9]。其中,SWMM模型是美国环保署(EPA)开发的城市暴雨管理模型,能够模拟城市降雨,广泛应用于我国城市雨水径流污染模拟[6]。关于模型应用方面国内外已经进行了许多研究工作,其中,模型参数敏感性分析和率定是研究重点[6,9-10]。早期关于SWMM模型参数率定的方法较少,以人工试错法和单参数敏感性分析法为主[11-12],主观性强且效率低,近几年随着计算机技术的发展,一系列自动寻优算法[13-14]直接被应用在产汇流模型参数识别和率定上,为避免陷入“维数灾难”[10,14],要按参数选择和参数率定这2个步骤进行。
本文以迁安市海绵城市建设研究范围作为模拟对象,对SWMM模型的水文、水质与LID措施参数进行选择,通过设计资料、人工试验、模型手册等确定参数来源,并根据相关文献[14-16]确定敏感度高的参数。参考模型手册和相关文献,采用拉丁超立方抽样(LHS)选取参数样本,进行参数率定和验证,确定参数最佳取值范围和最优值[17],提高参数率定的效率,为海绵城市建设和SWMM模型应用提供参考和借鉴。
1 研究范围概况
本次研究范围为迁安市海绵城市建设典型片区,其面积为25.24 km2,新、老城区结合,排水体制为合流制与分流制共存,其中,合流制区域为老城区,面积为2.6 km2,现状排水管网标准偏低,区域仅存一条排水出路(三里河),如图1所示。地处平原区域,地势平坦,属温带半湿润大陆性气候,雨热同期,雨季分明,降雨集中,6月—9月降雨量占全年降水量的80%以上。
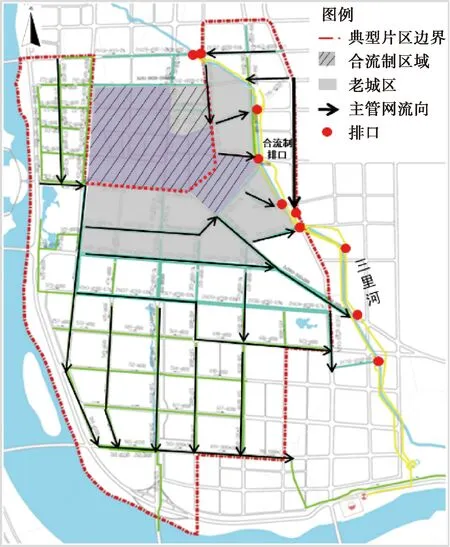
图1 研究范围Fig.1 Research Scope
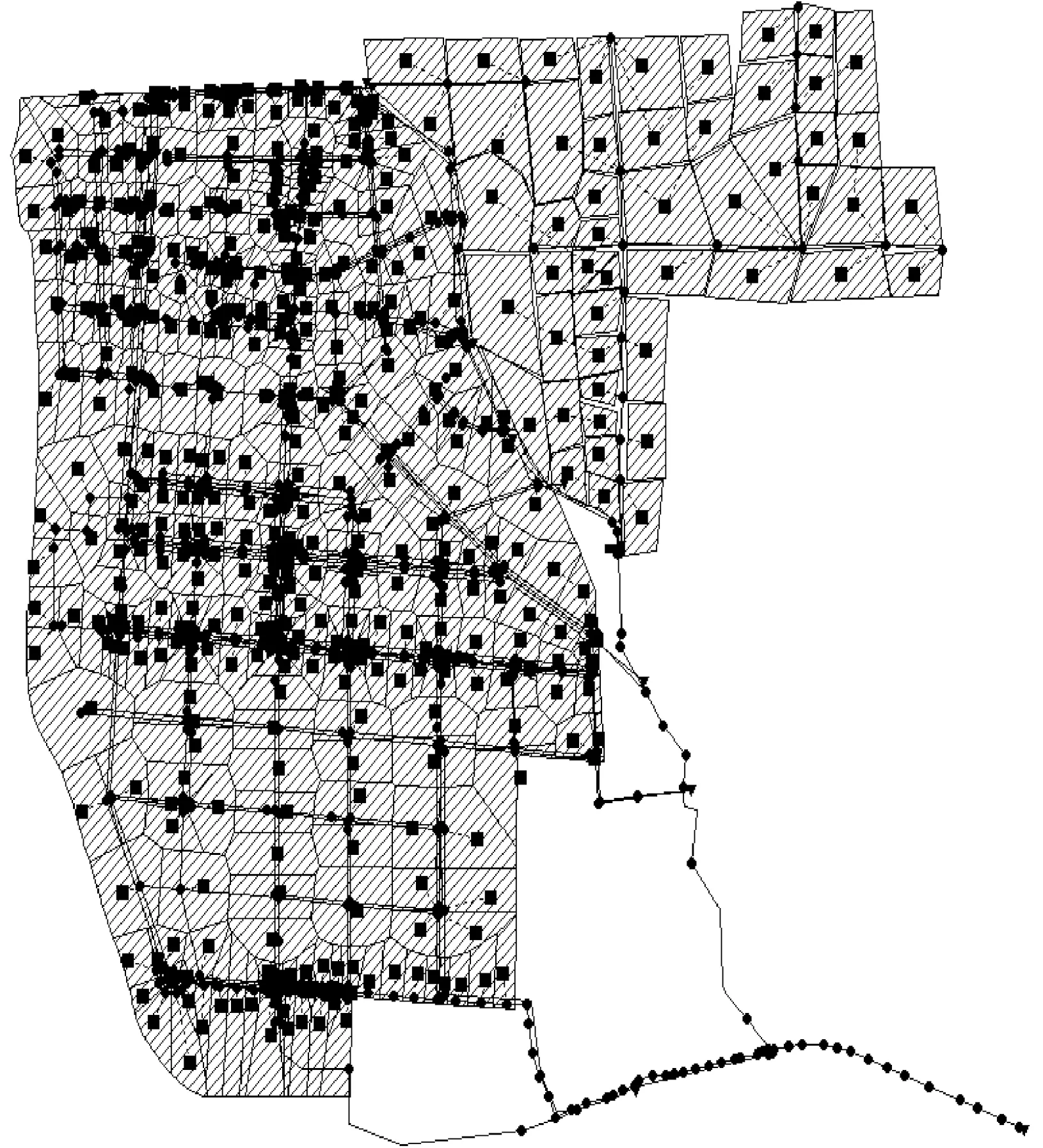
图2 模型构建图Fig.2 Model Building Diagram

图3 参数率定区域监测布点图Fig.3 Monitoring Points of Parameters Calibration in the Area
模型范围纳入典型片区外的老城区,整体概化为465个子汇水区、10个排水分区、管网756段(雨、污水)、节点705个(雨、污水),模型搭建情况如图2所示。在区域出口采用流速面积法和在线流量计监测流量,并采集水样进行水质监测,布设雨量计记录降雨数据,设置流量监测点共253个,水质监测点共122个(包括在线SS监测),雨量监测点共4个。其中,涉及参数率定区域为排水分区4、5、6,主要监测点(图3)包括旱季污水流量监测点(分区4~6的污水井1~4号)、雨季监测点(分流制雨水井5号、合流制排口6号)、典型项目丽都景苑监测点7号。LID设施面积为3 201 457 m2,包括透水铺装、下沉式绿地、生物滞留设施等。
选取2018年4月21和6月19日自然降雨进行水文模块参数率定和验证,降雨事件基本特征如表1所示,水质模块累积冲刷参数采用人工降雨试验数据进行计算和率定。
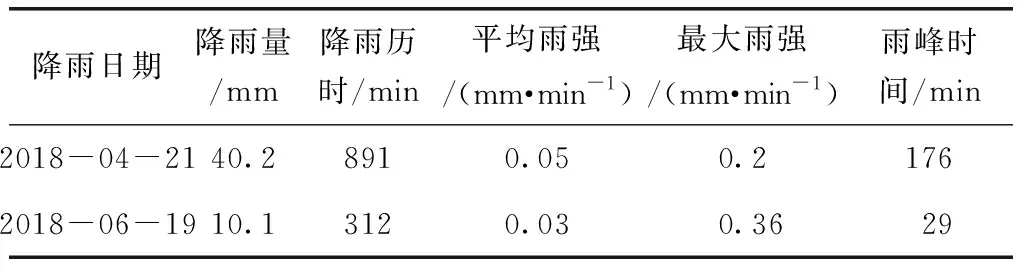
表1 降雨事件监测的基本特征Tab.1 Basic Characteristics of Rainfall Events Monitoring
2 参数选取与率定方法
2.1 参数选择
水文、水质参数与LID模型参数,参考模型手册推荐参数范围,通过设计资料、率定验证、人工降雨试验初步获得,如表2~表3所示。
2.2 参数率定方法
模型参数繁多,部分参数具有不确定性或概化结果不具实测意义的特征,无法直接通过测量得到,一般通过寻找一系列适合的模型参数,即优先分析参数的敏感性,并对敏感性强的参数赋值,使得模型的预测结果接近监测数据[14]。根据参数敏感性分析的相关文献[14-16,18],明确对曼宁系数、污染物累积冲刷参数等敏感度高的参数进行率定。在模型参数率定过程中,参考模型手册和相关文献,明确参数的先验分布范围,从中选择不同数值,直接进行参数率定和验证,或利用人工降雨试验数据,基于Matlab遗传算法模块,对模型进行参数率定[15],框架结构如图4所示。根据模型手册和文献[14-15],若选取的参数范围值过大,参数值离散度高,难以用简单回归的方法计算[19],因此,在参数的先验分布范围中,不断缩小取样范围,确定参数最优范围,再从中选取参数进行率定,得到参数最优值。

表2 水文和水质模块参数来源Tab.2 Source of Hydrology and Water Quality Module Parameters

表3 不同层中设施参数来源Tab.3 Source of Facility Parameters in Different Layers
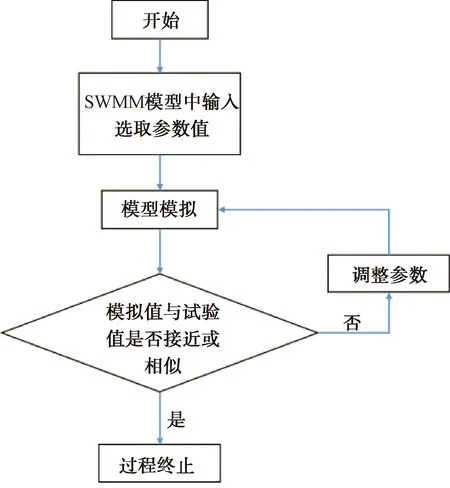
图4 遗传算法率定参数框架结构Fig.4 Framework Structures of Genetic Algorithm Calibration Parameters
研究范围是新老城区并存、合流制与分流制并存的区域,老城区现状管网陈旧、排水系统运行条件复杂,如监测数据或本底条件变化,易引起模型模拟工作量庞大、调节参数困难、推翻先验分布范围等情况出现,因此,找到更高效率、更精准的选参方法是十分必要的。常用的参数取样法包括蒙特卡洛法、单纯的分层抽样、LHS。
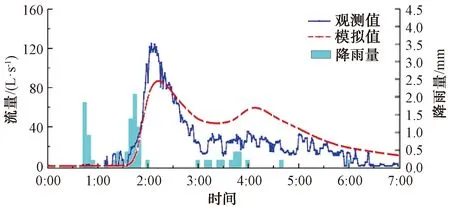
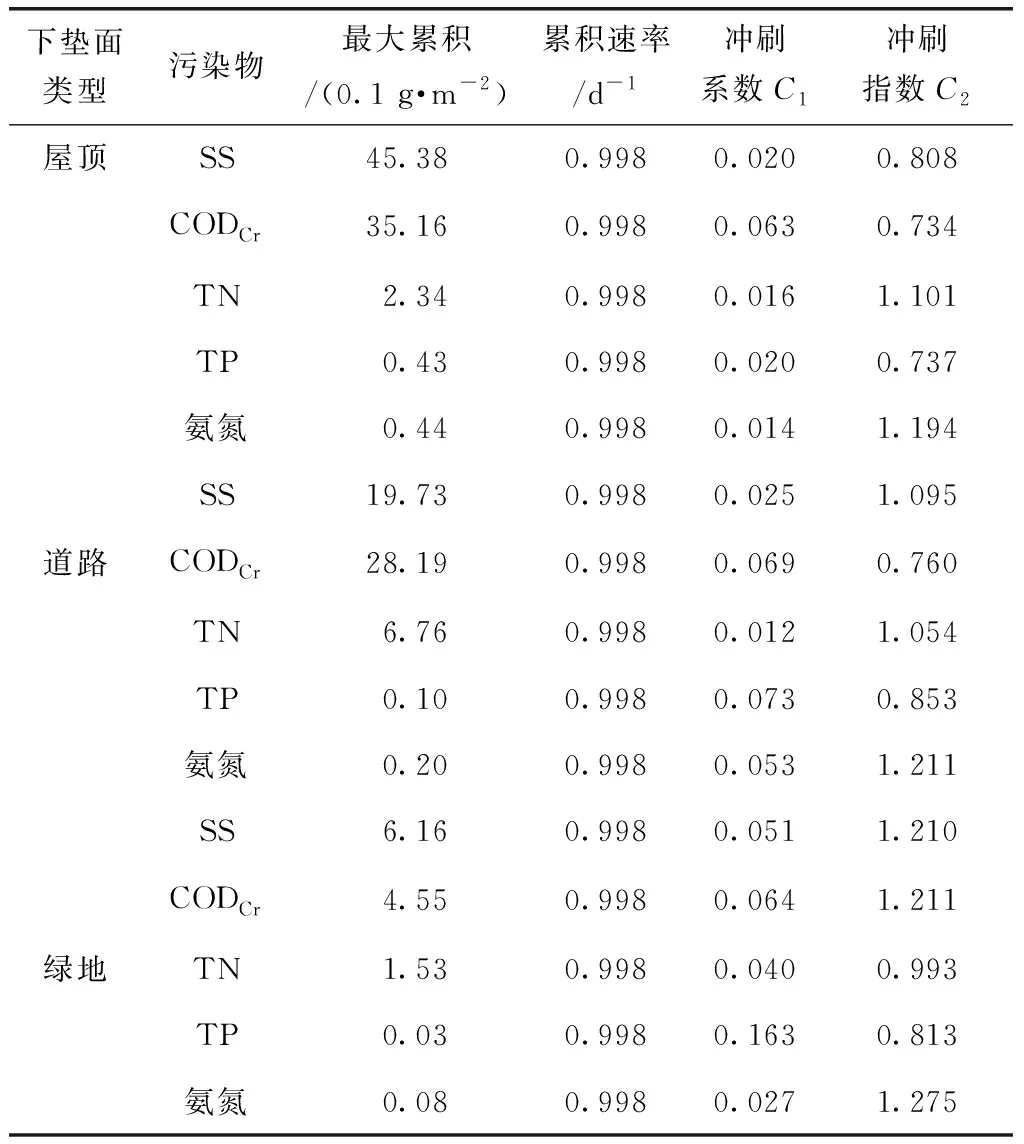
LHS是一种多维分层抽样方法,通过划分概率相等的间隔,从每个间隔中选取一个样本点[17]。其工作原理如下:(1)定义参与运行的抽样数目(N);(2)把每一次输入等概率地分为N列,把每一次输入等概率地分成N列,Xi0 相比蒙特卡罗模拟法的简单随机采样,LHS产生样本的空间覆盖率更高,样本的标准差较小,更高效和精准。相对于单纯的分层抽样,LHS的最大优势就在于任何大小的抽样数目都能容易地产生,效率更高[17],因此,采用LHS选取参数。 根据监测数据,判断模型模拟结果的准确性,选定精度判别指标纳什效率系数(NSE)[11],计算相应指标值,从而综合判断模型模拟的准确性。该指标是对结果总体误差的量化表示,不能捕捉局部的结果[6],NSE计算如式(1)。 (1) 搭建完整的产汇流模型,分别对水文、水质、LID措施参数进行率定与验证,技术路线如图5所示。 图5 模型参数选择与率定流程图Fig.5 Flow Chart of Model Parameter Selection and Calibration 图6 旱季率定径流量模拟值与观测值对比图Fig.6 Comparison between Simulated and Observed Values for Runoff in Dry Seasons 3.1.1 水文模块参数 (1)旱季率定 研究范围内涉及合流制区域,因此,需要对旱季污水管网曼宁系数N_Dry进行率定与验证。考虑数据获取难易度,采用2017年11月28日—2017年12月4日流量数据,涉及3个片区(图6),覆盖部分城区。参考模型手册确定管材N_Dry的先验分布为0.010~0.020,采用LHS法从中取样1 000次,同时模拟1 000次,计算NSE,取排名前2%的采样点,对应的N_Dry为最优取值范围。结果表明,最优参数取值为[0.901 7,0.901 9],确定N_Dry取值为0.012时,NSE为0.9,参数满足模型应用要求。 采用典型天的半点总流量数据进行旱季参数的验证,观测值和模拟值形状相似,主峰值出现时刻基本相同,如图7所示。验证NSE为0.944 8,取值可靠。 图7 旱季参数的验证径流量模拟值与观测值对比图(片区1)Fig.7 Comparison between Simulated and Observed Values of Dry Seasons Model Parameter Validation (Area One) (2)雨季率定 率定、验证特征宽度k_Width、不透水面曼宁系数N_Imperv、透水面曼宁系数N_Perv、雨季管网曼宁系数N_Wet。根据文献、模型手册,确定参数的先验取值范围(表4)。由于老、新城区的产汇流条件差异性大,需要采用2018年4月降雨事件分别率定。参考模型手册确定4个参数的先验取值范围,然后采用LHS从中对4个参数取样1 000次,同时模拟1 000次,取NSE排名前2%的采样点,其对应的参数值为最优取值范围(表4),与先验取值范围进行对比,N_Imperv和N_Perv参数的最优区间跨度大,参数并不敏感,而k_Width和N_Wet参数呈现了敏感特性,这与黄金良等[16]的研究成果相同,在参数最优取值范围内取靠近中间值为最优值(表4),流量过程模拟和观测值作图(图8)。 表4 雨季率定的最优参数区间和取值Tab.4 Optimal Parameters Range and Value of Calibration in Rainy Season 图8 雨季模型参数率定的模拟值与观测值对比Fig.8 Comparison between Simulated and Observed Values of Parameters Calibration of Rainy Season Model 图9 雨季模型参数验证的模拟值与观测值对比Fig.9 Comparison between Simulated and Observed Values of Rainy Season Model Parameter Validation 采用2018年6月19日降雨事件验证,观测值和模拟值形状相似,主峰值出现时刻基本相同,如图9所示。验证NSE为0.558 4,处于合理范围内,取值基本合理。 3.1.2 水质模块参数 根据冲刷函数,冲刷负荷计算如式(2)。 W=C1qC2B0 (2) 其中:W——冲刷负荷,g/h; q——单位面积的径流速率,mm/h; B0——污染物最大累积量,g。 冲刷负荷W可以由流量数据和污染物浓度数据计算得出,径流速率q可以由流量数据得到。根据屋顶、道路和绿地的人工降雨的试验结果,得到多场降雨的径流量和污染物浓度数据,明确累积冲刷方程中的冲刷系数C1、冲刷指数C2和污染物最大累积量B0。将径流速率q的观测值作为自变量,计算出每一组参数对应的模拟值(Wsim),与冲刷负荷W的观测值(Wobs)进行对比,使得所有W的观测值与模拟值最为接近的一组参数即为最优的参数。将不同下垫面类型的所有场次降雨的数据同时进行计算,其中屋顶和道路分别有5场降雨(55个W观测值),绿地有2场降雨(18个W观测值)。参考模型手册和相关文献,确定3个参数的先验分布范围(表5),采用Matlab遗传算法模块完成计算的工作[15,17],对于每一组参数进行10 000次采样,计算W的模拟值,与观测值进行比对计算NSE,选出最佳的参数。 图10 污染物冲刷负荷的观测值与模拟值Fig.10 Observed and Simulated Values of Pollutant Scouring Load 表5 累积冲刷参数先验分布范围Tab.5 Prior Distribution Range of Cumulative Scouring Parameters 以屋顶为例,各污染物的参数最优组如表6所示,显示最优参数对应的NSE,基本合格,观测值与模拟值对比(图10)。采用上述方法确定道路、绿地的污染物累积冲刷参数取值(表6)。 3.1.3 LID措施参数 对于非结构参数进行整体率定,根据SWMM手册与种植土试验数据,结合监测数据确定参数。选取2018年7月份的监测数据进行率定,8月份监测数据进行验证。经计算,NSE分别为0.83、0.79,验证NSE分别为0.66、0.62,均大于0.50,表明参数基本合理,如表7所示。典型项目模型参数率定与验证结果如图11所示。 根据《迁安市海绵城市试点区建设系统化方案》得到海绵城市建设指标和建设项目信息,采用典型年(2003年)分级降雨数据进行模拟分析,评估海绵城市建设前、后面源污染和径流量的产生情况,进而确定面源污染控制率和年径流总量控制率,经评估,面源污染削减率达到48.3%,年径流总量控制率达到76.6%,满足海绵城市建设目标。 表6 污染物累积冲刷参数取值Tab.6 Parameter Selection of Pollutants Accumulation Scour 表7 非结构参数率定值Tab.7 Unstructured Parameter Calibration 通过对迁安典型片区SWMM模型参数的率定和验证,得到以下几点结论。 (1)结合设计资料、人工试验和自然降雨条件下的监测数据,参考相关文献,提出水文、水质、LID措施模型参数率定验证的方法和技术路线,给出各参数的选取依据与路径,明确对曼宁系数、污染物累积冲刷参数等敏感性高的参数进行率定和验证。 图11 非结构参数率定与验证结果Fig.11 Results of Ustructured Parameter Calibration and Verification (2)在参数先验分布范围内,采用LHS选取参数样本,进行率定和验证,确定参数最佳取值范围和最优值,相比于人工选取、蒙特卡洛法和传统单层抽样法,提高了参数率定的效率。 (3)以迁安典型片区为例,确定了水文、水质、LID措施参数的最佳范围和最优值,为本地的海绵城市建设和国内SWMM模型应用提供了借鉴。但仍然存在值得深入研究的内容,如将LHS与Matlab遗传算法模块进一步结合,提出模型参数自动率定方法,以提高模型应用效率;研究参数取值与地势、管网运行状况等条件的规律,为北方平原城市的海绵城市建设提供借鉴。
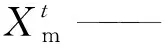
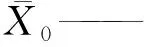

3 讨论
3.1 参数率定与验证







3.2 模型评估结果

4 结论

