长江经济带经济发展水平实证研究——基于STATA的面板数据分析

□ 程元栋，马曦腾

(安徽理工大学 经济与管理学院，安徽 淮南 232000)

1 引言

从经济学的角度来看，有效地刺激经济增长，推进经济发展从量变到质变是解决新常态下经济增长问题的重要手段[1]。长江经济带建设是我国实施的“三大战略”之一，其生产总值与人口占全国的比重均超过40%，在我国的经济发展中起到举足轻重的作用[2]。2016年发布的《长江经济带发展规划纲要》中提到要推进创新驱动开发、推进新型城镇化、构建完整开放格局、推进长江经济带开发。

目前，关于长江经济带的研究也有很多。周兵等[3]利用8年的平衡面板数据，建立了交互效应模型和阈值效果模型，分析了结构性去杠杆对经济增长的非线性影响。燕波等[4]借助环境库兹涅茨曲线与均值思想将不同的指数评估值置于不同的经济发展水平之下，通过结合熵方法计算环境性能指数。郭庆宾等[5]以长江经济带5个城市群为研究对象，比较研究了城市群间要素集聚能力差异。李雪松等[6]利用DEA Malmquist测量出长江经济带2000-2014年经济增长的总体效率水平以及全要素生产率并且采用105个城市的面板数据，运用tobit检验了区域一体化对全要素生产率、技术效率以及技术变动的影响。

本文通过STATA进行四种分析，即相关分析、回归分析、因子分析和聚类分析。何叶荣等[7]选取皖江城市群10个城市为研究样本，提取9项指标作为研究对象，使用STATA软件，采用多元统计综合评价方法，对10个城市的经济发展能力进行比较与评价。刘博雷[8]从5个分类中选取24个指标，主要采用了相关性分析、线性回归、聚类等方法，对中国36个主要城市的经济社会发展水平进行分类、分级和综合评价。

2 数据来源及研究方法

本文借鉴了国内外相关研究，为了保障所选指标具有全面性、代表性和可操作性等特征，考虑了地方经济发展总值和经济发展的效率、质量等因素[9]，在《中国统计年鉴》上获取长江经济带11省市2018年的截面数据，选择了9个研究对象，其中m1表示省市名称，m2为地区生产总值，m3为财政一般预算收入，m4表示常住人口，m5为货物进出口总额，m6代表城镇居民可支配收入，m7代表农村居民可支配收入，m8为社会消费品零售总额，m9表示第二产业增加值。

研究方法是使用STATA软件，对所选指标采取相关分析、回归分析、因子分析和聚类分析。首先，进行相关分析和回归分析，研究长江经济带经济发展与各个指标之间的相关关系；再使用因子分析，提取出各个指标的因子，找出最具有代表性的指标；最后，采用聚类分析对各个省市的经济发展能力进行分类排名。

3 实证研究

3.1 数据描述性分析

本文的研究指标中的数据除了省市名称是字符串变量外，剩余的都是数值型变量，可以直接进行描述性统计，得到关于研究指标数据的主要统计结果，通过这些结果可以整体把握那些用来分析的数据，为后续进一步的数据分析做好必要的准备。使用STATA导入相关数据，在命令窗口输入命令summarize m2-m9,detail，就得到了相关的描述性统计的结果。由于对其中的8个指标都进行了分析，我们就以m2(地区生产总值)为例进行详细的阐述，如表1所示。

表1 m2描述性分析结果

从表1中可以看出，m2这一变量的百分位数中，15353.21，20880.63，21588.8，22716.51为四个最小值，而四个最大值分别是42021.95，42902.1，58002.84，93207.55;它们的均值为38456.91，标准差也可以得出是21948.61;偏度显示为正偏态，其值是1.43976；4.576541表示的是其峰度。通过描述性分析结果分析可以看出，所有研究指标的数据中不存在极端数据和异常数据，数据间的量纲差距也均可接受。

3.2 相关分析

使用STATA，在命令窗口输入命令pwcorr m2-m9,sidak sig star(0.01)，就得到了相关分析的数据结果，结果展示的是各个研究指标之间的相关系数，如表2所示。

从表2中可以看出，有5组指标是具有很强的关联性，并且在0.01水平上显著。它们分别是m3(财政一般预算收入)与m5(货物进出口总额)，其相关系数为0.9788；m6(城镇居民可支配收入)与m7(农村居民可支配收入)，它们的相关系数为0.9748；m2(地区生产总值)与m8(社会消费品零售总额)，其相关系数为0.9777；m2(地区生产总值)与m9(第二产业增加值)，其相关系数为0.9876；m8(社会消费品零售总额)与m9(第二产业增加值)，其相关系数为0.9614。与此同时，我们也对其他的研究指标的相关性进行了分析，发现它们两两之间的相关性不很显著。

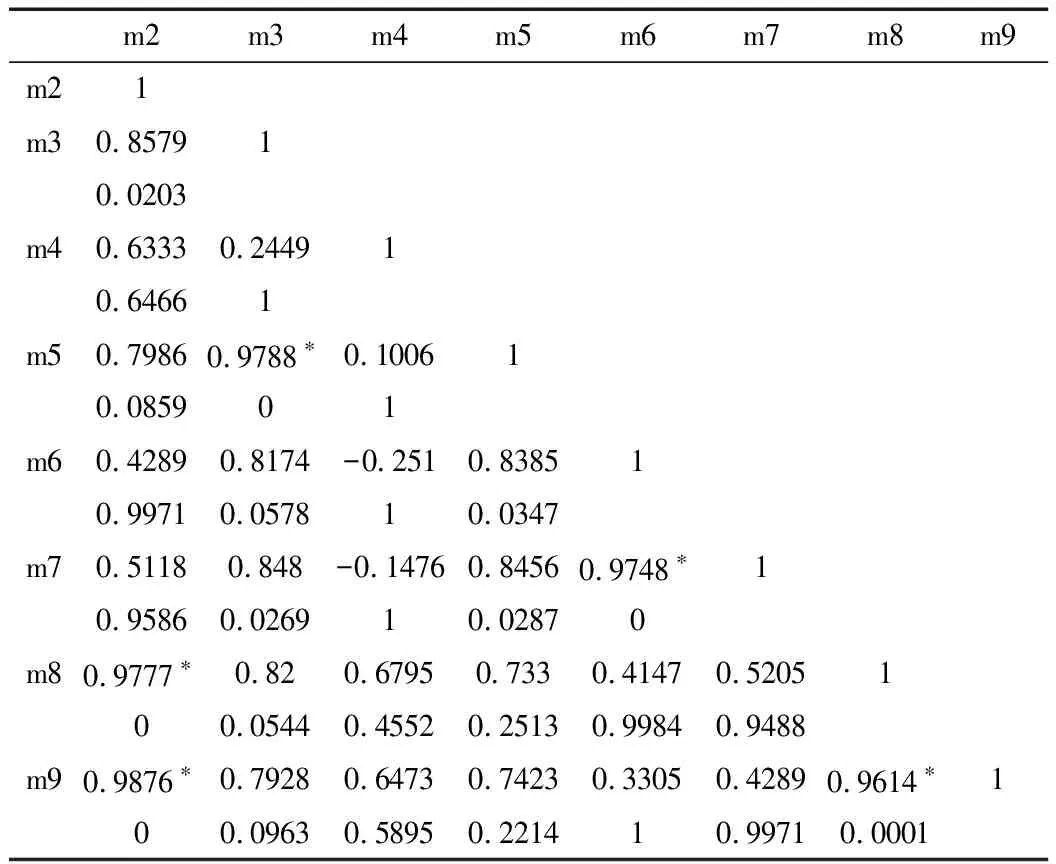
表2 相关分析结果

3.3 回归分析

3.3.1 模型构建与模型修正

由于各种研究变量之间的影响比较复杂，本文以地区生产总值为因变量，以财政一般预算收入、常住人口、货物进出口总额、城镇居民可支配收入、农村居民可支配收入、社会消费品零售总额、第二产业增加值为自变量，进行多重共线性回归。在命令窗口中输入命令sw regress m2 m3-m9,pr(0.1)，得出回归分析的结果，如图1所示。

图1 回归分析结果

从图1中的分析结果可以得出，参与分析的样本有11个，模型的F(4,6)=1229.77，P值(Prob>F)为0.0000，据此可以看出，整体上，模型是非常显著的，模型的可决系数(R-squared)是0.9988，模型修正的可决系数(Adj R-squared)高达0.9980，说明模型具有非常好的解释能力。

模型采用的是逐步回归的方法，最终结果是经过3次剔除变量所得到的。第一次剔除前是包含全部自变量的模型，该模型中m4变量的P值为0.8193，被剔除；第二次剔除是模型中的m5变量，其显著性P值为0.2073；第三个被剔除的变量是m6，它的P值为0.4268。以上自变量剔除后得到了最终的回归模型。

在最终的回归模型中，变量m3、m9、m8、m7的P值都小于0.005，系数都非常显著。最终最小二乘回归模型的方程为m2=3.90498m3-0.6489966m7+0.8394437m8+0.8848854m9+7638.314。即地区生产总值=3.90498*财政一般预算收入-0.6489966*农村居民可支配收入+0.8394437*社会消费品零售总额+0.8848854*第二产业增加值+7638.314。

3.3.2 异方差检验

在STATA命令窗口中输入predict mm2。在数据编辑器区域出现mm2的值，发现其值和m2的值较为接近，由此可以看出拟合的回归模型是比较好的。之后在命令窗口中分别输入estat imtest,white和estat hettest,iid和estat hettest,rhs iid。这些命令用来进行异方差检验，分别代表怀特检验，拟合值对数据的BP检验，方程右边的解释值对数据的BP检验。检验结果见表3。

表3 异方差检验结果

通过分析结果可以得出：怀特检验时，P值为0.3575；拟合值对数据的BP检验时，P值为0.9054；方程右边的解释数据进行BP检验时，P值为0.5954；三个命令的P值均大于 0.05，非常显著接受了同方差的原假设，认为不存在异方差。所以，不需要使用稳健的标准差进行回归[10]。

经过以上回归分析，可以得出，长江经济带的地区生产总值与财政一般预算收入、农村居民可支配收入、社会消费品零售总额和第二产业增加值有显著关系，且在这四个变量中，财政一般预算收入、社会消费品零售总额和第二产业增加值对地区生产总值起正向促进作用；而随着农村居民可支配收入的增加，地区生产总值呈现下降趋势。其他变量与地区生产总值有一定关系，但并不显著。

3.4 因子分析

本文使用主成分分析对长江经济带进行因子分析。在STATA命令窗口中输入factor m2 m3 - m9,pcf，得出因子分析结果，如表4所示。

表4a 因子分析结果

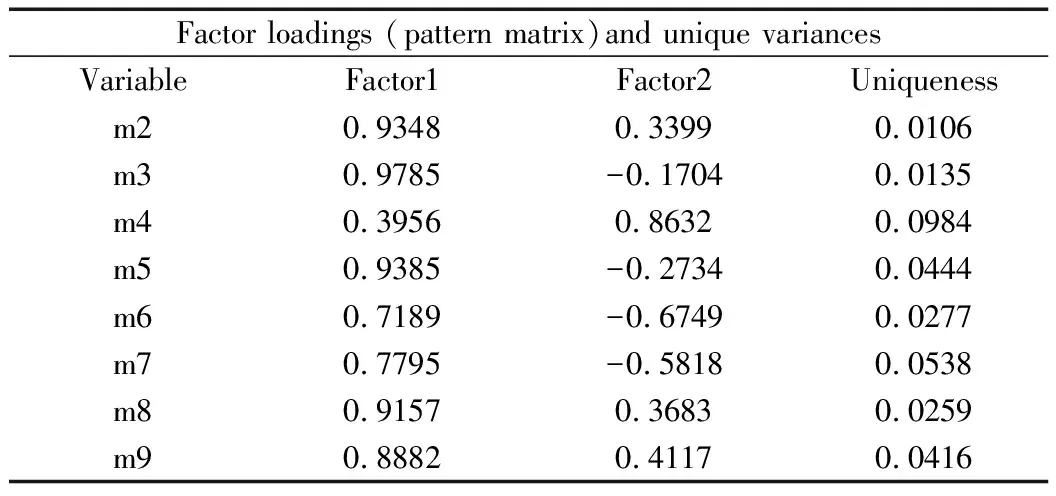
表4b 因子分析结果

在选取的因子中特征根大于1的只有2个，选取这2个因子分作为新的综合评价指标，其P值=0.0000，说明模型非常显著。这两个成分已经可以解释原始数据中96.05%的信息。

接下来采取最大方差正交旋转法[11]对因子结构进行旋转。在STATA命令窗口中输入rotate,得到的结果如图2所示。

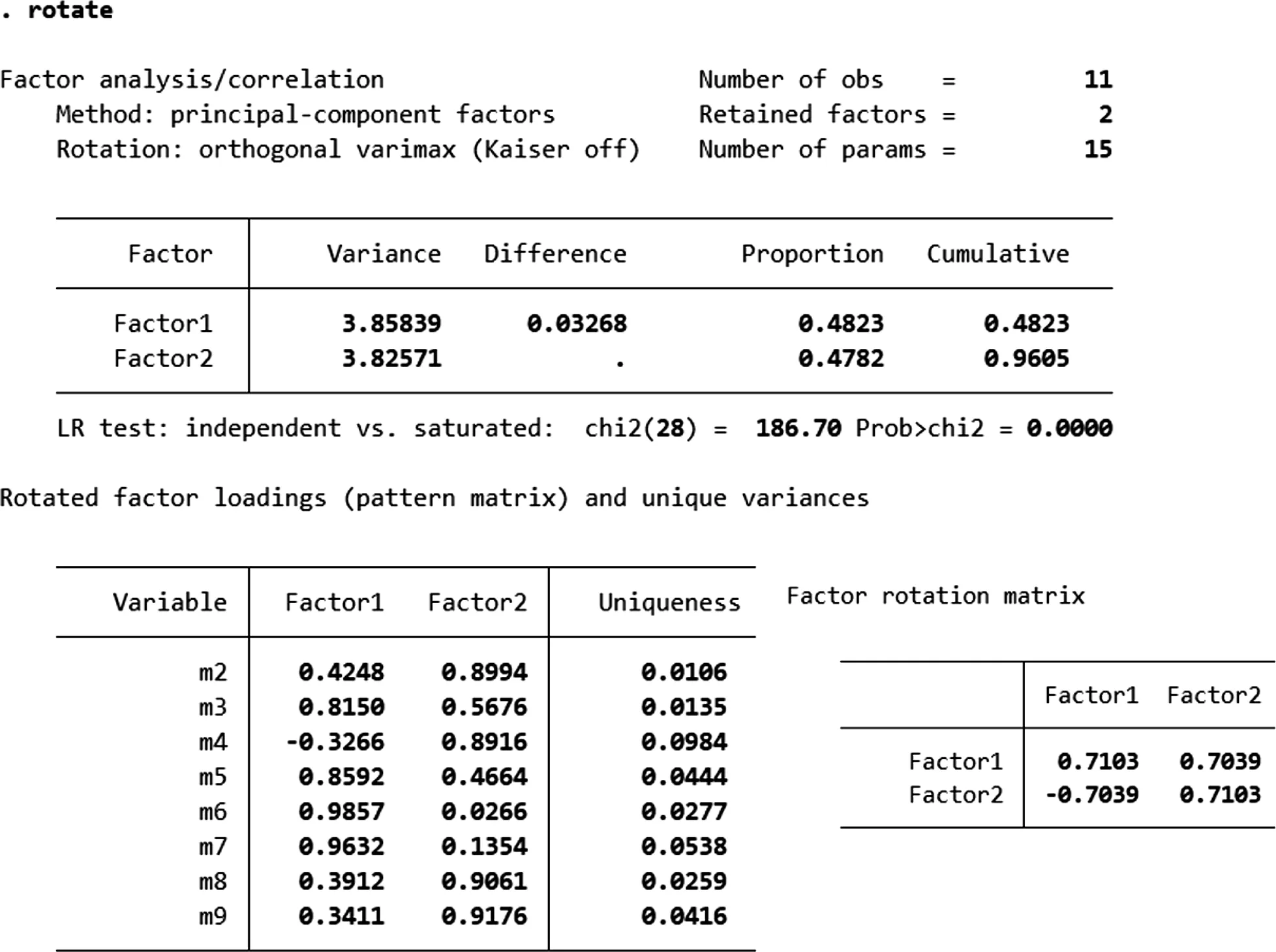
图2 最大方差正交旋转结果

结果共展示3个部分，第1部分是通过因子旋转模型得出的一般情况，可以得出旋转后的模型依然可以解释原始数据中96.05%的信息。第2部分显示是旋转后的因子载荷图，第一因子主要解释的是m3、m5、m6、m7这些变量的信息；第二因子主要解释的是m2、m4、m8、m9这些变量的信息。第3部分展示的是提取的2个因子相关关系不明显。

接下来在命令窗口中输入predict f1 f2展示各个研究指标的因子得分状况，可以通过得分写出各个因子的表达式。即f1=0.00221m2+0.1818m3-0.24442m4+0.21188m5+0.32105m6+0.29696m7-0.00991m8-0.02817m9；f2=0.23407m2+0.06387m3+0.34667m4+0.02341m5-0.14229m6-0.10265m7+0.24126m8+0.25295m9。

再在命令窗口中输入correlate f1 f2展示2个主成分间的相关关系，从结果来看，相关关系很不明显[12]。这也表明采用因子进行正交旋转方式是合适的，结果如图3所示。

图3 因子得分与相关性结果

在命令窗口中再输入scoreplot,mlabel(m2)yline(0)xline(0)，得出每个样本的因子得分示意图，见图4。从图中可以发现，每个样本的因子都直观、清晰地分布在四个象限[13]。

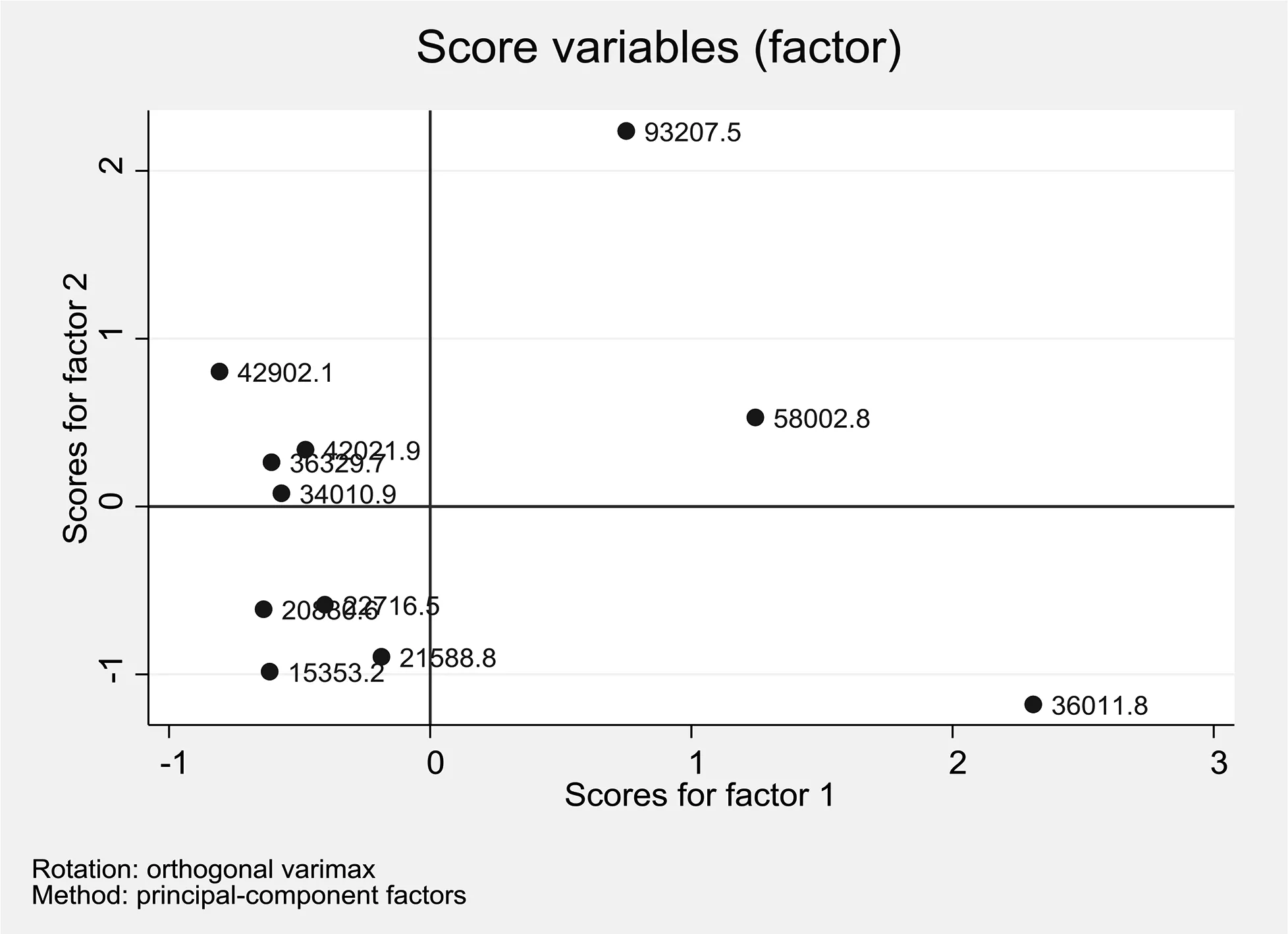
图4 因子得分示意图

为了更好地分析各个省市的区别，本文计算出各省市的综合得分。在命令窗口输入generate f=0.4832*f1 +0.4782*f2 和sort f，就可得出各个省市的综合得分并排序，f1、f2 前面的系数为各个因子旋转后的方差贡献率。综合得分可用来衡量各个省市的经济社会发展水平，结果如表5所示。

4 结果分析与评价

由表5可知，在长江经济带11个省市经济社会发展水平排名中，江苏位列第一，其次是浙江和上海，贵州在11个省市中排名最低，得分为-0.76734。

对综合得分使用 K均值聚类分析和散点图分析，在命令窗口中输入cluster kmeans f,k(3)。将长江经济带11个省市经济社会发展水平分为3个等级，结果如表5所示。

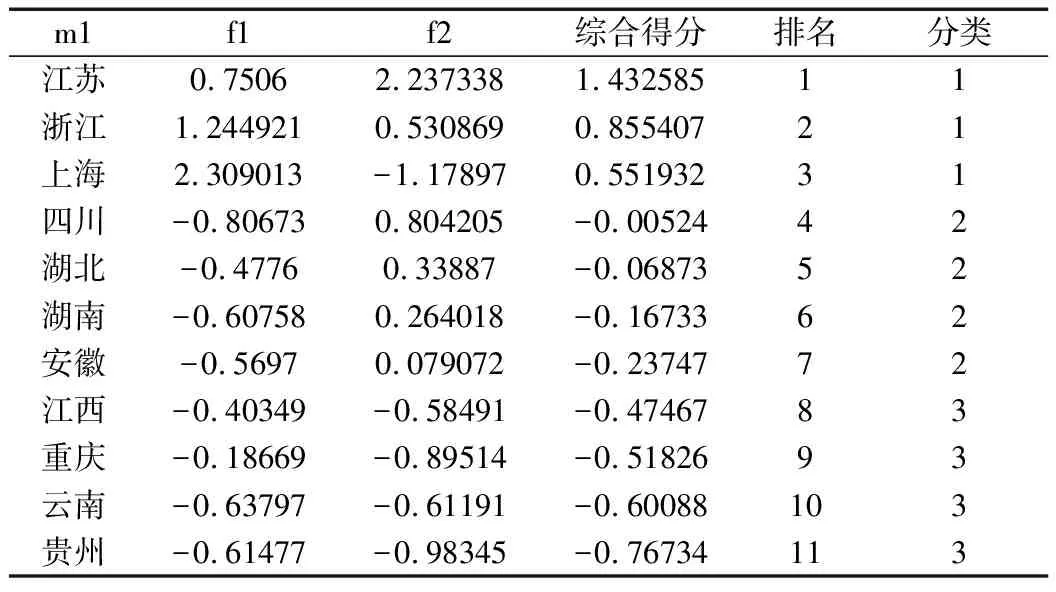
表5 各省市的因子得分、综合得分、排名和分类

第一等级为水平较高的省市，依次是江苏、浙江和上海。以江苏为例，江苏在f2方面最为突出，位于该因子的首位，说明江苏在地区生产总值、社会消费品零售总额、第二产业增加值这四类指标中均为各市之首；但在f1方面只能排到第3位，主要是因为城镇居民可支配收入、农村居民可支配收入与第一等级的其他省市相比较低。

第二等级是水平中等的省市，有四川、湖北、湖南和安徽。以四川为例，四川是第二等级的翘楚，在f2方面也很突出，位于该因子的第2位，它在常住人口这一指标中位于各省市之首，社会消费品零售总额位于所有省市中的第四位；但其在f1方面的得分为-0.80673，是所有省市中的最后一名，这是由于其城镇居民可支配收入为第10名，农村居民可支配收入为第9名造成的。

第三等级为水平较低的省市，有江西、重庆、云南和贵州。以贵州为例，其在f2方面是所有省市的最后一名，为-0.98345分，原因是地区生产总值、社会消费品零售总额和第二产业增加值这三项指标位于所有省市的最后；在f1方面，贵州位于第10名，也不太理想，在f1的财政一般预算收入、货物进出口总额、城镇居民可支配收入和农村居民可支配收入这几项指标中都位于最后一名。

综上，要使长江经济带的综合整体能力得到提高。首先，必须找到各自的发展优势和劣势，找寻机会，充分发挥各自的优势，并合理地规避风险，推动长江经济带内外的合作，不断加强地区利益协调机制的建设，进行多元化投资[14]；其次，发展快速的省市群将走科技经济发展之路，加强与经济带内各省市的协同创新发展，促进科技进步，实现整体综合经济实力的大幅提升；之后，明确不同等级省市的功能定位，促进长江经济带内各地区政府、企业、高等学校和研究机构合作，并积极整合各类资源，多方资源的充分共享可以提高长江经济带整体的实力[15]；最后，要加强基础设施建设、信息网络建设，为长江经济带综合经济能力发展提供保障。