基于图网络融合的交通状态预测方法研究
2022-05-12徐东伟商学天魏臣臣
徐东伟 商学天 魏臣臣 彭 航
(浙江工业大学网络空间安全研究院1) 杭州 310023) (浙江工业大学信息工程学院2) 杭州 310023)
0 引 言
近年来,有大量的方法模型应用到不同场景下的交通路网预测上,并取得了丰硕的成果.在统计学习算法模型中,文献[1]通过引入最大相关熵的Kalman滤波器,制定了交通流预测任务.对于K最近邻(K-nearest neighbor,KNN)算法在交通预测领域的应用,文献[2-3]提出了一种基于核K近邻算法的时间序列预测道路交通状态的算法,构建了时间序列道路交通状态数据序列的核函数,将当前和参考道路交通状态的数据序列相匹配,基于此k选择最接近的参考道路交通状态并预测道路交通状态.
随着深度学习的兴起,神经网络方法在处理交通路网数据预测问题时有显著的优势.文献[4]提出了一种基于图卷积LSTM(GC-LSTM)的序列到序列(Seq2Seq)模型,该模型利用图卷积网络(graph convolutional network,GCN)处理交通路网空间特征,LSTM处理交通路网时间特征,可以很好地解决长期交通流量预测问题.生成对抗网络(GAN)作为近年来复杂分布上无监督学习最具前景的方法之一,文献[5]展示了卷积层与GAN的组合,弥合CNN在有监督学习的成功与无监督学习之间的差距.图神经网络(graph neural networks,GNN)[6]作为一种基于图域分析的深度学习方法,靠图中节点之间的信息传递来捕捉图中的依赖关系.但是,对于图卷积神经网络(graph convolutional network,GCN)[7]等图节点学习方法,如文献[8]根据路网拓扑结构与交通流时空相关性提出基于GCN的短时预测模型,很难处理类似于出现新节点等未知节点问题,不能直接泛化到未知道路.文献[9]提出GraphSAGE框架,通过训练聚合节点邻居的函数,使GCN扩展成对未知节点起到具有归纳学习能力的作用.但是,该框架只对道路节点之间的空间相关性进行特征提取,而交通道路节点存在着紧密的时间关系.
为了捕获道路节点之间的时间相关性,文中根据历史道路状态数据构建基于时间相关性的逻辑相关路网,利用GraphSAGE图聚合算法对路网进行特征提取,并融合两个不同路网的时空特征信息.以最小化损失函数为目标,返回最优模型参数,构建基于图网络融合的交通路网模型.
1 基于GraphSAGE特征融合的路网交通状态预测模型
基于GraphSAGE特征融合的路网交通状态预测算法模型,见图1.对于横纵复杂的道路交通,选取历史路网状态数据X′=[X(s-1),X(s-2),…,X(s-c)],X(s)为第s时刻的交通路网状态数据,c为历史交通路网状态的时间长度.为了构建交通原始路网G=(V,E),在N条道路上放置道路检测器,其中:V={v1,v2,…,vN},vi(i∈1,2,…,N)代表第i个检测器节点,检测器检测的是交通节点;选取与节点vi之间在空间上为连边关系的节点集合,记为N(vi),若第i个检测器vi代表的道路节点与第j个检测器vj代表的道路节点存在相邻,则eij=1,反之:eij=0,E={eij}Ni,j=1,表示邻接矩阵,通过邻接矩阵构建的原始交通路网反映道路节点与节点之间的空间关系.为了构建基于时间相关性的逻辑相关路网,根据每个道路节点vi的历史道路状态数据xi=[xi1,xi2,…,xiS],S为历史数据中的数据量,重构交通路网;采用GraphSAGE分别对原始路网与重构后的基于时间相关性的逻辑相关路网进行时空特征提取,并对路网特征进行特征融合,预测得到未来路网状态数据Z=[X(s),X(s+1),…,X(s+n)],n为未来路网状态的时间长度.
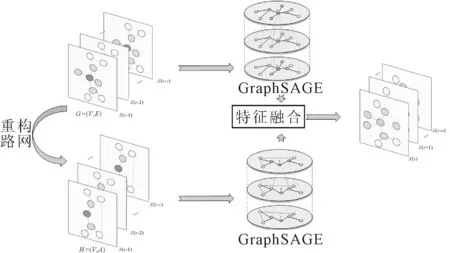
图1 基于GraphSAGE特征融合的路网交通状态预测算法模型
1.1 基于时间相关性的逻辑相关路网构建
原始路网表现出交通道路节点之间的空间关系,并且节点之间存在着基于道路历史交通状态数据的时间相关性.为了计算出各路网节点之间的相关性,见图2.

图2 构建逻辑相关路网
对于每个检测器道路节点vi,根据历史道路状态数据xi,用皮尔逊相关性系数计算公式为
式中:K为在计算皮尔逊相关性系数时所选取的检测器表示的交通路网状态节点数据的长度.通过得到不同检测器之间的皮尔逊相关性系数,得到路网G的x*x的皮尔逊相关性系数矩阵E={rij}xi,j=1.

重构得到逻辑相关路网H=(V,A),其中A={aij}xi,j=1,aij表示第i个检测器vi与第j个检测器vj之间存在的连边关系:

1.2 基于GraphSAGE的路网特征提取
使用GraphSAGE图聚合算法来聚合道路交通节点的邻居顶点蕴含的信息,见图3.

图3 GraphSAGE算法流程图
为了充分提取道路节点的邻居特征,通过聚合函数把与节点具有连边关系的邻居聚合特征,再与道路节点拼接转换,得到节点在第t层的特征,t=(1,2,…,T):


根据原始路网和构建的基于时间相关性的逻辑相关路网,对道路邻居节点的每个维度取平均.通过均值来表达道路节点邻居在时间与空间上的相关性分布,均值聚合函数为
为了捕获道路节点之间在时空上最突出的的表现,先对邻居节点进行非线性转换后,选取道路邻居节点的每个维度最大值,maxpooling聚合函数为
1.3 基于特征融合的路网状态预测



式中:WT,b为模型待学习的参数;σ为Sigmoid函数.
2 实验
2.1 数据描述和实验设置
实验数据集分别采用西雅图2017年的高速路网速度数据和加州2016年7—8月的流量数据,其中西雅图数据集共计323个检测器,速度数据采样间隔为5 min;加州原始数据集共计170个检测器,但是,原始数据集中含有大量的缺失值,因此只挑选含有完整数据的道路,处理后共计114个检测器,流量数据采样间隔为5 min.实验设计为根据历史交通路网数据来预测未来5,15,30,45和60 min的交通路网数据,其中历史交通路网数据选取0~3 h中每隔30 min的时间,见表1.由表1可知:由于加州数据集是车流量数据,并且数据波动比较大,不利于在较短时间的历史交通路网数据中做预测实验;而西雅图数据集是速度数据,数据波动比较平缓,西雅图数据集与加州数据集在历史交通路网数据分别为1 h与2 h30 min的情况下,预测结果最好.文中实验皆选取该两段作为历史交通路网数据.

表1 本文实验数据集在不同历史交通路网数据下的预测结果
在基于特征融合的GraphSAGE交通路网数据预测模型中,交通路网检测器节点个数N为各自数据集的道路节点个数,每个节点的特征即训练的时间步长F分别为12与30,训练集与测试集划分比例a=0.8,输入模型的路网数据使用min-max标准化;在构建基于时间相关性的路网结构计算皮尔逊相关性系数时,选取的每个检测器节点历史交通状态数据长度K=288×F=3 456,皮尔逊相关性系数较大的检测器节点的选取比例设置为p;GraphSAGE均值聚合的层数T,每一层的隐藏单元个数从分别为2T-1×16,激活函数σ为ReLU激活函数;重构误差系数α=100,均采用Adam优化器优化模型参数.
2.2 文中方法的参数选取
使用平均相对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)来比较不同预测方法的准确度.其定义分别为

表2为在GraphSAGE图聚合算法中的均值聚合算法下不同选取比例下的误差指标.

表2 在不同选取比例下的误差指标
由表2可知:西雅图数据集与加州数据集分别在选取比例p为0.10与0.30时,获得的预测结果最好;与其他选取比例相比,MAE和MAPE均有着显著提升.此外,从表中能明显看出,两个数据集一个在低比例结果好,一个在高比例结果好,这是因为西雅图数据集检测器更多,选取高比例则会造成许多相关性非常小的邻居节点分配到比以往更多的权重,从而导致不能充分聚合道路邻居节点的信息,所以在选取比例低时,道路节点的邻居分布更适合表示道路节点之间的时间特征;而加州数据集的检测器少,所以选取比例较高时获得的结果更好.
表3为文中提出的基于特征融合的模型利用GraphSAGE图聚合算法在不同层数下的两种聚合器得到的误差指标.
由表3可知:在西雅图数据集中,使用均值聚合算法的本文方法得到的预测结果优于maxpooling聚合算法,并且T=3的时候结果最优;在加州数据集中,均值聚合的MAE与RMSE优于maxpooling聚合,其中选取聚合层数T=3.西雅图与加州数据集皆在均值聚合算法中得到较好的结果,可能的原因是两个数据集均是高速公路数据集,相比于城市路网,高速路网的节点之间连接稀疏,所以当使用maxpooling聚合时,容易把与该节点无关的节点加入到maxpooling计算中,并导致聚合的邻居信息失去有效性.而对于高速路网,利用均值聚合算法可以有效地捕获邻居节点信息.

表3 两种GraphSAGE图聚合算法在不同聚合层数下的误差指标
2.3 对比实验
表4为对比实验中各模型的参数设置.其中,T-GCN方法中GRU的隐藏层单位数为64;ConvLSTM方法中,设置了三层ConvLSTM层,每层中卷积核大小为3×3,卷积核数目为32.

表4 对比实验中各模型的参数设置
图4为文中两个数据集的对比实验结果.其中,T-GCN方法是由GCN来捕获空间依赖性,门控循环单元结构(GRU)来捕获时间关系;ConvLSTM方法通过CNN提取空间特征,并且由LSTM方法建立时序关系.

图4 文中数据集对比实验的误差指标
由图4可知:构建的基于时间相关性的逻辑相关路网的结果均优于原始路网,证明了逻辑相关路网在捕获道路节点之间的时间关系的有效性;文中利用融合特征的方法在相同参数条件下,对比于原始路网的RMSE提高了21.17%,表明了文中方法在精度方面也有不错的提升.其中,对比于新型GCN模型,本文方法在对未知节点处理中具有的归纳学习能力能够更好的对未来路网数据进行预测;对于西雅图数据集,文中方法对比于图节点的学习方法GCN与T-GCN,在短时间预测15 min时,MAE提高了53.2%与30.5%;而对比于时间序列方法LSTM与ConvLSTM,在较短时间预测30 min时,RMSE提高了38.5%与40%,表现出文中方法优越性.此外,可以明显看出时间序列方法在较长时间预测时,结果并不理想,而文中方法和基于原始路网的GraphSAGE图聚合方法在短时5~60 min的时间段内的预测结果比较平缓,具有一定的稳定性.
2.4 文中方法的预测能力分析
分别采集2017年1月3日(星期二)与8日(星期日)的西雅图高速路网d005es15280检测器全天的288个数据.图5为该检测器在1月3日预测不同未来时间步长的残差箱型图,箱型图由中位数,上下四分位数,上下边界等统计量构成来表示数据的分布情况.由图5可知:文中方法在预测未来30 min内的路网数据偏差较小,并且大部分偏差集中在-2~+2范围内,表明本文方法在短时交通路网预测具有一定的精确度;但是在预测未来45与60 min时,中位数与0相差较大,预测准确度不高.

图5 d005es15280检测器预测结果残差箱型图
使用文中方法与LSTM方法训练完成的模型对该数据集进行预测,图6为数据预测结果.
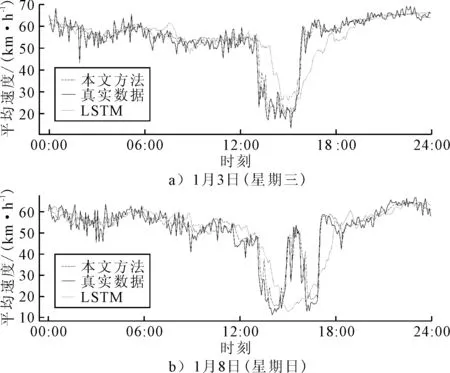
图6 d005es15280检测器在工作日与休息日的预测结果
由图6可知:文中方法相比于LSTM方法得到的预测值更加接近真实值;其中13:00时开始,由于交通拥堵,平均速度明显降低,此时,LSTM方法的预测具有滞后性,不能够实时准确预测,而本文方法的拟合能力出色;并且在1月8日(星期日)14:00—16:00中,下午出现了少有的拥堵缓和的情况,LSTM方法对于类似突发情况不能够如文中方法一样做到精准预测.
3 结 束 语
文中对西雅图2017年的高速路网速度数据与加州2016年7—8月的流量数据进行实验分析,建立了基于GraphSAGE特征融合的路网交通状态预测算法,该模型引入相关性系数来重构交通路网,得到的逻辑相关路网表示道路节点之间的时间相关性,从原始交通路网与基于时间相关性的逻辑相关路网中提取特征,特征融合后对路网未来交通状态数据进行预测.实验根据历史交通路网数据来预测未来5,15,30 min,1 h的交通路网数据,通过参数与模型的对比,说明了构建基于时间相关性的逻辑相关路网的有效性,并与其他传统预测方法进行比较,文中特征融合方法对未来路网交通状态数据的预测能力最优.在未来的工作中,将对更多的聚合函数进行实验比较,并进一步优化模型相关参数,不同的迭代次数,隐藏层节点数目等,都会对模型准确率产生影响.
