基于近似法的LED光源寿命预测
2022-05-12伍玉莹孟庆慧黄海松
伍玉莹,李 晟,孟庆慧,周 武,黄海松
(江西理工大学理学院,赣州 341000)
0 引言
近年来,固态照明广泛应用于工业和生活的各个领域,发光二极管(LED)作为新一代绿色光源,以其高效率,长寿命,稳定性高,相对环境友好(它们不含汞)且功耗低等优点,开启了照明领域的新革命。近几年,我国LED市场规模快速扩大,2018年中国LED 照明行业市场规模达到5985 亿元,2019年中国LED 照明行业市场规模达到6823 亿元,年增长率达到14%,预计未来将会继续保持高速增长。相比于传统的照明产品,LED 照明产品具有易于智能控制的特点,其与智能控制系统相融合的智能照明产品能够实现照明设备的开关、节能、检测等功能。智能照明是满足消费者个性化照明等要求的有效方案,受到照明企业以及智能控制企业的热捧,具有极大的发展潜力,而LED 作为智能照明产品重要的组成部分,也将受到相关企业的关注。LED 照明正逐步取代传统照明技术,主导着照明市场的发展方向。LED 照明产品逐渐渗透路灯照明、景观照明等领域;还可以在农业生产中用作人工光源以提升农业产量;LED 光源具有消炎、杀菌等医疗效果,在人体诊断与治疗方面存在广泛应用。LED 照明应用领域广,应用前景非常开阔。LED 已经成为当前时代最主要的照明解决方案之一,因此,如何对LED 灯进行准确的寿命预测逐渐得到广泛的关注。吴志杰等提出了一种新型的基于遗传算法(GA)优化的误差反向传播(BP)神经网络的寿命预测模型。选取不同公司生产的LED,以LED 光源光通量维持率测量方法(LM-80-08)测试报告中的电流、结温、初始光通量和初始色坐标作为神经网络的输入,LED 在网络输入的应力条件下的寿命为输出,可以预测LED 在任意电流和结温下的寿命。一般情况下,流明维持寿命(L)是衡量LED 照明的性能、寿命和可靠性的最合适的特性,且目前大多数LED 制造商基于建立寿命预测分析。一般来说,LED 寿命是指一般照明的寿命。本文基于6000 小时或更多的流明数据,采用近似法对LED 进行寿命预测。先利用NLS回归方法对其进行曲线拟合,根据拟合得到的曲线方程预测LED 的流明维持寿命,再采用近似法处理拟合所得到的数据,进行LED可靠性的分析和评估,并将近似法的评估结果与TM-21标准预测方法进行对比讨论。
1 基本方法理论
1.1 NLS回归方法
NLS 回归方法是以误差的平方和最小为准则来估计非线性静态模型参数的一种参数估计方法。该模型参数的非线性组合的函数取决于一个或多个独立变量。其中,观测数据通过函数建模获得,数据再经过逐次逼近的方法进行拟合。NLS回归方法的具体步骤如下:
(1)对LED 的光通量数据进行归一化处理,选取平均值,得到样本的流明维持率数据。
(2)利用NLS 回归方法,根据公式(1)对LED的流明维持率数据进行曲线拟合。
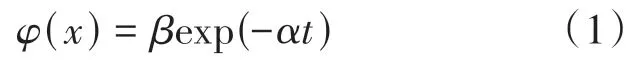
其中,()为在时间的光通量归一化平均值,即流明维持率;,皆为曲线拟合系数,为常数。
(3)对式(1)进行对数变换,即得到LED 寿命预测模型:
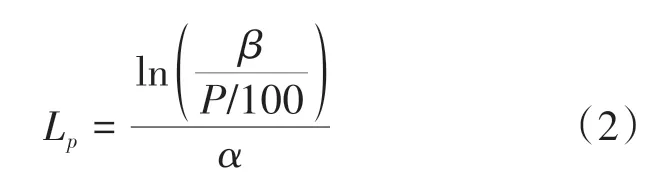
其中,L是LED 的流明维持衰减到初始值的%时的寿命(在本研究中采取=70)。
1.2 近似法
近似法根据一般的退化模型对每个单元的失效时间进行预测,并在退化路径达到临界失效阈值D时投影到“伪”失效时间。对于一般的退化路径模型,假设随机样本量为,测量时间为,,,…,t。第台机组在第次试验时的性能测量称为y。因此,退化路径可以表示为时间性能度量对(t,y),(t, y),(t,y),…,(t, y),对于=1,2,…,n,m表示每个单元的测试时间点
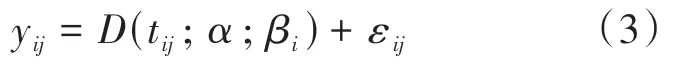
其中,(t;; β)为测量时间t时单元的实际退化路径。是固定效应向量,每个单位的固定效应保持不变。β是随机效应向量,它随不同的单元而变化。ε表示单位在时间t的测量误差,该时间假设为零均值和方差为的正态分布。
近似法步骤如下:
(1)根 据 数 据(t,y),(t,y),(t,y)…,首先使用NLS 方法估计退化路径模型的参数(固定效应参数和随机效应参数β)。
(2)将每个单元的退化路径模型外推到临界失效阈值D。当(t;; β)= D时,每个单元的“伪”故障(非实际故障)时间可以预测。
(3)拟合这些“伪”寿命数据的概率分布,并估计分布的相关参数。
(4)根据分析可靠性函数()、MTTF 评估样本的可靠性
2 IES TM-21标准基本理论
IES TM-21 是根据LM-80-08 报告推荐的一种流明维护寿命预测方法,TM-21 所用数据即为LM-80-08 报告中数据,IES TM-21 推荐的样品规模集最小为20,当报告中数据的测试持续时间为6000 小时至10000 小时,数据集中用于曲线拟合的数据应该是最后5000 小时的数据。1000 小时以前的读数,不用于曲线拟合。对于测试持续时间大于10000小时的数据集,在总体测量持续时间的50%点以后的数据都应用于曲线拟合。换句话说,在/2到之间的数据都应用于曲线拟合。例如,如果测试持续时间是13000 小时,使用的数据应该是6500 小时至13000 小时之间测量所得。如果没有/2 点的测量数据,则下一个稍低时间点的数据应该包含在拟合数据集内。例如为13000 小时,则每1000 小时采集一次数据,则使用6000 小时至13000小时之间的数据作为拟合数据。
3 实验结果
3.1 NLS拟合结果
本文数据源于LM-80-08报告,其数据包括了对LED 光通量20个单元的流明维护数据6000个小时的测试点(间隔时间1000 小时),初始1000 小时后以1000 小时的间隔作为拟合数据,按照第1节所示的NLS操作步骤,以每个测试时间的流明维持数据用于使用NLS 方法拟合LED流明衰减曲线,图1是其中某一单元的预计流明寿命,拟合曲线参数估计和流明寿命结果如表1所示。
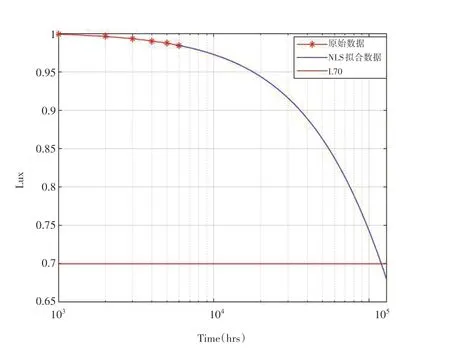
图1 流明寿命L70测试图
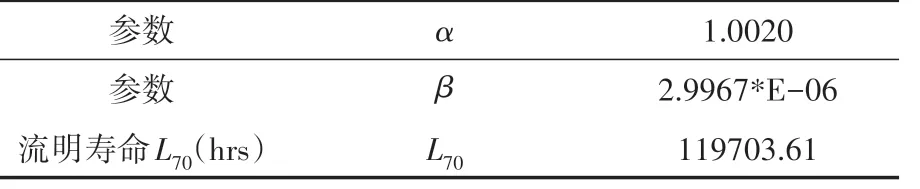
表1 衰减模型参数估计和流明寿命L70
3.2 近似分析法实验结果
使用非线性最小二乘方法,对每个单元的一般退化路径模型进行估计,如图2 所示(左边是右边方框的放大),然后通过将每个单元的模型外推到临界故障阈值(光照减少到70%),预测“伪寿命”,如表2所示。

表2 20个单元退化的参数及伪寿命
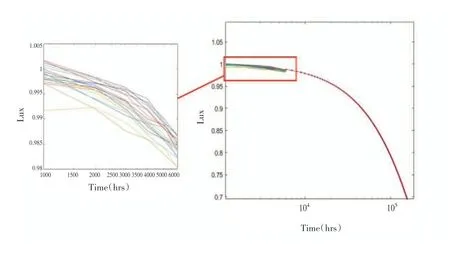
图2 数据退化路径
确定从外推法获得的“伪寿命”的概率分布。为了更精准地对LED 使用寿命进行预测,本文选择了随机变量概率密度函数——威布尔分布(Weibull)、对数为正态分布的随机变量的连续概率分布——对数正态分布(Lognormal)、实值随机变量的连续概率分布——正态分布(Normal),此三种不同类型的统计模型对“伪寿命”进行拟合。拟合结果如图3所示。
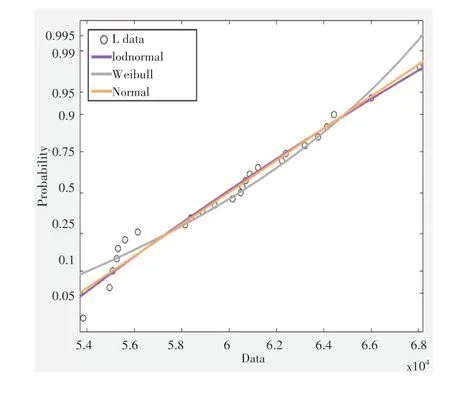
图3 “伪寿命”统计模型拟合
建立在信息论的基础上,利用统计模型的拟合优度的方法之一——Akaike 信息准则(AIC),对给定的数据集进行预测误差估计。AIC不仅可以处理过度拟合的风险和不足拟合的风险,还可以通过验证分析得到分布满足威布尔模型时所表现出最好的拟合性能。以下是其可靠性函数:
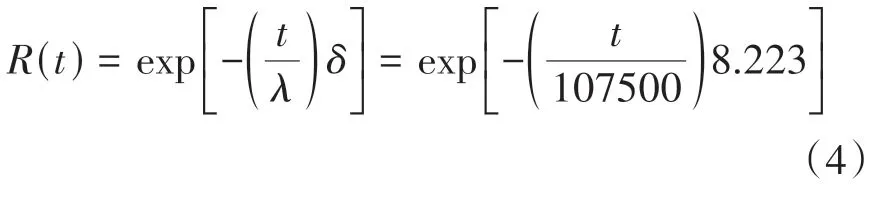
其中与分别为Weibull分布的参数。
最终,利用最大似然估计法可得结果如表3所示。

表3 结果参数
综上所述,由于近似法忽略了测量误ε,因此存在一定的局限性。但是,相比与NLS 回归方法,近似法还提供了更加充足的可靠性信息(可靠性函数、MTTF……),有利于客户更清楚、全面地了解产品,对市场进行更为有效的评估,以达到精准生产和投入的目的。
4 结语
基于LED 的照明是现代最具影响力的照明时代的技术之一,在节能减排的背景下,社会各界对高效的LED 照明产品的关注程度达到一个新的高度,LED 已经逐渐发展成目前发现的普遍照明应用中,应用范围广、成本低、能耗低、稳定性高且高度可靠的光源。不过,迄今为止尚且没有标准方法可以达到实际测量LED完整寿命的水平。而对LED 进行寿命评估可以在一定的误差内间接地获取LED 的寿命数据,因此,对LED 进行较为精确的寿命评估至关重要。为进一步推广LED 高效、合理的运用,本文采取近似法预测和分析LED 的发光器件寿命。近似法先通过利用NLS 方法,拟合出每个单元的失效时间,然后再对失效概率分布模型进行拟合,从而得出LED 的一般退化路径模型。与TM-21 标准预测得到的结果相比,近似法不仅可以有效地提供更多的信息,还提供了结果的可靠性,利于开发者更加方便地决策不同寿命LED的市场应用范围。
